Открытый урок по математике в 6 классе. Тема Решение уравнений

Министерство образования и науки РД Кайтагский район

МКОУ «Баршамайская СОШ им. Качмасова А.Р.»

План – конспект открытого урока по математике. 6 класс.

Тема: Решение уравнений.

Учительница: Хидирбекова Айзанат Гаджиахмедовна.

Открытый урок по математике в 6 классе.

Тема урока: «Решение уравнений»

ЦЕЛИ УРОКА:

1.ПОЗНАВАТЕЛЬНАЯ: -сформировать умение и навыки решать уравнения, а также умение составлять уравнения при решении задач.

2. РАЗВИВАЮЩАЯ: формировать умение ориентироваться в новой обстановке;

3.ВОСПИТАТЕЛЬНАЯ: учить умению рассуждать, высказывать свои мысли отстаивать свою точку зрения.

ОБОРУДОВАНИЕ:

• Презентация к уроку;

• Карточки с заданиями

РАЗВЕРНУТЫЙ КОНСПЕКТ УРОКА.

Девиз урока:

«Уравнение - это золотой ключ,

открывающий все

математические сезамы»

С.Коваль

І. Организационный момент.

Здравствуйте! Садитесь… (Слайд 1)

II. Актуализация опорных знаний

1. В начале урока на экране вам представлен кроссворд, заполнив который мы повторим основные понятия и теоретические факты которые нам сегодня пригодятся.

Угадав все слова и записав их в клеточки по горизонтали, в выделенном вертикальном столбце вы прочтете тему нашего сегодняшнего урока. (Слайд № 2)

1. Как называют расстояние в единичных отрезках от начала координат до точки А(а)? (Модуль)

2. Как по-другому называют равенство двух отношений? (Пропорция)

3. Как называется результат от деления? (Частное)

4. Как называются числа, отличающиеся только знаками? (Противоположные)

5. Как называется число, которое можно записать в виде отношения а/n, где а – целое число, а n – натуральное число? (Рациональное)

6. Как называются числа, которые получаются в результате расширения множества натуральных чисел, за счет добавления к ним нуля и множества отрицательных чисел? (Целые)

7. Арифметическое действие, обратное действию деления? (Умножение)

8. Если выражение является произведением числа и одной или нескольких букв, то это число называют …? (числовым коэффициентом)

9. Число, которое не делится нацело на 2, называют…? (нечетным)

Разгадав кроссворд, в выделенном вертикальном столбце ученики читают слово «уравнение».

Итак, тема нашего сегодняшнего урока - уравнение. (Слайд 3)

Запишите в тетрадях число и тему сегодняшнего урока и положите ручки.

Рассмотрим цели нашего урока. (слайд 5)

• сформировать умение и навыки решать уравнения, а также умение составлять уравнения при решении задач.

• повторить теоретический материал по теме

Сегодня мы продолжаем решать уравнения, а какие вы узнаете чуть попозже. Давайте вспомним, что мы уже знаем:

- Уравнением называется….

- Корнем уравнения называется….

- Уравнение может иметь (?) корней.

-Чтобы перенести какой-нибудь член уравнения из одной части в другую, надо….

- Обе части уравнения можно умножить на ….

Диалог учеников.

Первый ученик: Итак мы знаем, что уравнение можно решить, если перенести его члены из одной части в другую.

Второй ученик: Просто перенести и всё?

Первый ученик: Нет, не просто. Если мы перенесём какой-нибудь член уравнения, например, из левой части в правую, то обязательно должны поменять его знак.

Второй ученик: Ну это не трудно. Этот способ решения даже легче, чем применявшийся раньше. Не нужно помнить множество правил. Скажи, а если в уравнении есть скобки, мы перенесём член уравнения прямо со скобками?

Первый ученик: Ну что ты? Скобки сначала надо раскрыть, а потом переносить известные члены уравнения в одну сторону, а неизвестные - в другую.

Второй ученик: Я понял. Значит в уравнении 12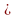 (у-2) = 3 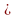(2у-8)+12 сначала раскроем скобки: 12у-24 = 6у-24+12

Первый ученик: А дальше решаем как обычно. Ну что, начнём?

12у – 6у = -24 + 24 =12

6у = 12

у = 2

Ответ: у = 2

III. Формирование умений и навыков учащихся.

1. Решить задачу. Найти сколько весит батон.

Ответ: 2 кг

1. Сейчас вам предстоит решить уравнения. Если вы укажете номер правильного ответа, то вам откроется часть красивой фотографии.

х – 3 = 12

6х = 18

3х - 8= 16

12 - 2х = 4х

5х +45 = 45

2х – 4 = 3х – 1

2(5х – 9) = 9х + 1

8х = - 20 – 2х

17 = 3х – 1

х +17 = 77 – 4х

5х + 18 = 3х

8х = - 8

6(3х – 4) = 3х – 9

1. Внимание! Внимание! В школу пришло необычное сообщение. Просят помочь семья Ивановых. Вот письмо, послушайте.

Обращаемся к вам с большой просьбой. Наш дед всю свою жизнь занимался математикой. Написал несколько научных трудов, которые хранил в сейфе. Недавно его не стало. Он хотел, чтобы мы опубликовали его работы. Но прежде, чем открыть сейф, нужно знать код к нему. Дед дал нам ключ к коду, но остался верен своей любимой науке и для того, чтобы узнать нужные 4 цифры, необходимо сделать вычисления, математикой больше в семье никто не увлекается и много со школьных лет забылось. Помогите узнать код к сейфу, будем за это очень признательны. Ключ к коду: положительные корни уравнений расположенных в порядке возрастания.

1). 4х + 12 =3х + 8 (Ответ: х=–4)

2). 3х-17 = 8х – 18 (Ответ: х=7)

3). 2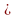 (8+у) = 3у+12 (Ответ: у=4)

4). -3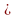 (с-5) = -2 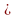(с-3) (Ответ: с=9)

Итак, код к сейфу: 4 7 9.

- Как вы думаете, смогли ли мы помочь семье Ивановых?

Да, я с вами согласна. Вижу, что вы усвоили решение уравнений.

1. ФИЗКУЛЬТМИНУТКА:

На разминку

На разминку становись!

Вправо-влево покрутись

Повороты посчитай,

Раз-два-три, не отставай, 

Начинаем приседать —

Раз-два-три-четыре-пять.

Тот, кто делает зарядку,

Может нам сплясать вприсядку. 

А теперь поднимем ручки

И опустим их рывком.

Будто прыгаем мы с кручи

Летним солнечным деньком. 

А теперь ходьба на месте,

Левой-правой, стой раз-два. 

Мы за парты сядем, вместе

Вновь возьмёмся за дела. 

1. Уравнения часто используют в повседневной жизни, но о том, как возникли уравнения, кто их придумал, не думаем. Иногда полезно знать, кто это сделал, ведь если бы не эти люди, то возможно и по сей день не придумали бы как решать уравнения. Решив первое задание и выбрав правильный вариант ответа, узнаем, где впервые, согласно дошедшим до нас рукописям, стали известны линейные уравнения и приемы их решения.

Решите уравнение: (-20х-50)·2=100 (х = - 5)

Более 4000 лет назад в Древнем Вавилоне и Древнем Египте уже были известны приёмы решения линейных уравнений.

Р ешив следующее задание вы узнаете, какого древнегреческого математика, умеющего решать очень сложные уравнения, по праву называют «отцом алгебры».

(х=18)

Ответить на вопрос о том, кто, где и когда ввел первые уравнения невозможно, но решение первых уравнений связано с именем замечательно ученого Диофанта, жившего в третьем веке н. э. в г. Александрия. Он придумал два основных приема решения уравнения, которыми мы пользуемся и в настоящее время (правило приведения подобных членов и правило прибавления или вычитания к обеим частям уравнения одного и того же числа или выражения). Он умел решать очень сложные уравнения, применял для неизвестных буквенные обозначения, ввел специальный символ для вычитания, использовал сокращения слов.

Р ешив следующее задание вы узнаете, кто впервые написал учебник алгебры и описал в нем методы решения уравнений.

(х=3)

Из истории математики известно: в 8 веке н. э. хорезмский математик Аль-хорезми в своих научных трудах описал методы решения уравнений, которые сводились к двум операциям: перенос слагаемых из одной части в другую назывался аль-джебр и приведение подобных слагаемых – валь-мукабала. Постепенно слово аль-джебр перешло в название науки «алгебра». А что же такое алгебра? Среди задач, которые с давних времен приходилось решать людям, много было похожих, однотипных: вычисление площадей участков, нахождение объемов фигур определенной формы, деление доходов, вычисление стоимости товара, измерение массы с помощью различных единиц и другие. Для таких задач в разное время, в разных странах пытались отыскать общие способы, правила решения. В этих правилах раскрывалось, как найти неизвестную величину через данные числа для группы похожих задач. Так возникла алгебра - один из разделов математики, в котором вначале в основном рассматривалось решение различных уравнений.

1. Игра «Найди ответ»

Решить уравнение и найти его на участнике игры.

2х + 5 = 7х (х = 1)

- 9х + 5х = 16 (х = - 4)

3х – 6 = 9 – 2х (х = 3)

7 + 4х = 3 (х = - 1)

6х – 13 = 3х + 5 (х = 6)

4х – 10 = 6 – 4х (х = 2)

1. Итог урока.

2. Рефлексия

Фамилия Имя______________________________________________________________

Сегодня на занятиях было интересно, потому что_________________________________

__________________________________________________________________________

Я бы хотел похвалить себя за то, что____________________________________________

__________________________________________________________________________

Я понял, что_______________________________________________________________

__________________________________________________________________________

Было трудно_______________________________________________________________

__________________________________________________________________________

Меня удивило______________________________________________________________

__________________________________________________________________________

На уроке понравилось, ______________________________________________________

__________________________________________________________________________

Запишите домашнее задание в дневник: №1341(а,б,в), 1343.

Список используемой литературы:

1. Н.Я.Виленкин Математика для 6 класса.

2. Поурочные планы по учебнику Н.Я.Виленкина.

3. П.И.Алтынов Контрольные и проверочные работы по математике.