Учитель математики МБОУ СОШ №1 с. Кизляр Магометова Х.Н
Открытый урок "Решение рациональных уравнений".
Цель: "Способствовать формированию умений применять приемы сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию; развитию творческих способностей учеников путем решения заданий, содержащих модули, параметры."
Учебник: Алгебра и начала математического анализа. 10 класс. Учебник. Никольский С.М. и др. (2009, 430с.)
Тема: § 2. Рациональные уравнения и неравенства. П. 44
Тема: Решение рациональных уравнений
Развитие и образование ни одному чело-
веку не могут быть даны или сообщены. Вся-
кий, кто желает к ним приобщиться, должен
достигнуть этого собственной деятельно-
стью, собственными силами, собственным
напряжением. Извне он может получить
только возбуждение.
А.Дистервег
Цели:
1. Обобщить, углубить знания школьников по изучаемой теме.
2. Способствовать формированию умений применять приемы сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию; развитию творческих способностей учеников путем решения заданий, содержащих модули, параметры.
3. Побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.
Ход урока: Вы знаете - чтобы решать уравнения нужно совершать ряд преобразований, и делать это следует очень осмотрительно. Например, решая уравнения, мы могли бы рассуждать так:
| Пример 1 | Пример 2 |
| 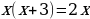
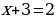
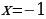
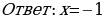
| 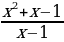 = =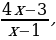
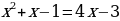 , ,
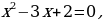
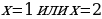 , ,
Ответ: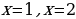
|
На самом деле, стараясь «избавиться от всего лишнего» , мы допустили ошибки. Какие?
(В результате неравносильных преобразований в уравнении 1 потерян корень 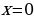 , а в примере 2 появился «посторонний» корень
, а в примере 2 появился «посторонний» корень 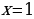 )
)
-Как же не попасть в подобные ловушки?
(Прежде всего нужно четко понимать, какие действия нужно выполнить в ходе решения уравнения)
-Сегодня на уроке мы повторим, обобщим, приведем в систему изученные виды и приемы решения рациональных уравнений.
Предварительное домашнее задание
Задание 1. Решить уравнения 1-12 и провести классификацию уравнений по виду.
Ответы
1. 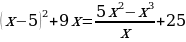
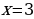
2. 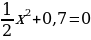 Нет действительных корней(
Нет действительных корней(
3. 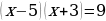
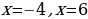
4. 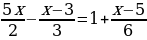
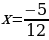
5. 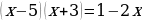
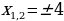
6. 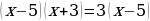
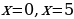
7. 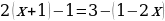 Нет действительных корней
Нет действительных корней
8. 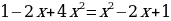 х= 0
х= 0
9. 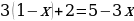 Бесконечное множество корней
Бесконечное множество корней 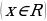
10. 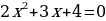 Нет действительных корней(
Нет действительных корней(
11. 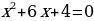

12. 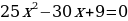
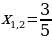
В
Виды уравнений ууравнени
результате выполнения задания получилось схема 1.
в
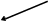 Ввиды ввв
Ввиды ввв


Целые рациональные
Дробно-рациональные (при-водимые к виду  =0,где
=0,где 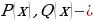 многочлены,
многочлены, 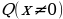 №1
№1




Линейные (приводимые к виду 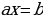 )
)
№4,7,9
Квадратные (приводимые к виду 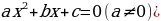




Приведенные
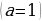
№3,11.
Не приведенные
 )
)
№10,12







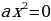
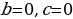
№8
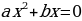
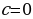
№6
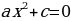
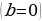
№2,5
Полные 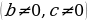
№3,10,11,12
Неполные, приводимые к виду
(У доски разбирается наиболее интересный пример)
-В результате обсуждения и проверки домашнего задания выясняем сущность решения уравнений.
Выводы:
-
Уравнением с одним неизвестным называется запись вида 
-
Областью определения уравнения называют множество всех значений 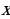 , при которых определены обе части уравнения
, при которых определены обе части уравнения
-
Корнем или решением уравнения называют значение неизвестного, при подстановке которого в уравнение получается верное числовое равенство. Решить уравнение -значит найти все его корни или доказать, что их нет.
-
Линейные и квадратные уравнения решаются по готовым формулам, они называются простейшими. Главная задача при решении любого уравнения -свести его к простейшему
Результаты выполнения домашнего задания заносятся учащимися в оценочный лист.
Оценка: «5»-нет ошибок; «4»-2-3 ошибки; «3»- более 3 ошибок.
Этап II
Цель: установить связи между корнями квадратных, линейных уравнений и их коэффициентами
Укажите, о чём идёт речь?
(Уравнение 1 имеет бесконечное множество корней
Уравнение 2- решений не имеет
Уравнение 4 имеет один корень
Уравнение 3- линейное уравнение с параметром. В зависимости от значения параметра а уравнение может иметь различное количество корней.)
| 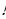
| Решить уравнение с параметром a- это значит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению. |
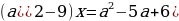
Решение.
Случай 1. 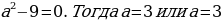 .
.
Если a=-3, то исходное уравнение примет вид 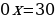 и корней не имеет.
и корней не имеет.
Если 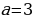 , то получаем уравнение
, то получаем уравнение 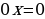 , для которого любое действительное число является корнем.
, для которого любое действительное число является корнем.
Случай 2: 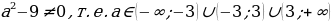
Выразим 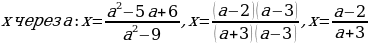
Ответ: если a=-3, то корней нет;
если a=3, то 
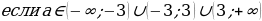 ,то один корень
,то один корень 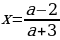
Работа в группах( работа с карточками):

Квадратные уравнения (приводимые к виду 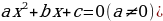






D
D=0
D0
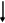
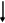
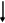



Один корень
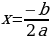
Корней нет
Два корня
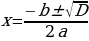
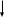
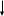




Линейные уравнения (приводимые к виду 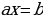 )
)


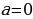
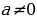


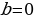
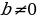

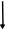
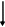






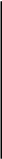


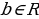
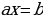

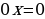
Бесконечное множество корней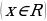
Нет действительных корней 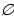
Один корень 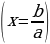
Учитель предлагает группам учащихся собрать на доске из заранее подготовленных карточек схему 2 и схему 3,которые отражают связь числа корней квадратного уравнения 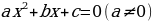 с его дискриминантом
с его дискриминантом 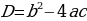 , и для каждого случая аналитического решения указать геометрическую модель.
, и для каждого случая аналитического решения указать геометрическую модель.
Что бы это означало?
((1) и(3) - квадратные уравнения с параметром. В этих уравнениях параметр а входит в состав второго коэффициента и свободного члена. (2) - это также уравнение с параметром, но параметр а входит в состав коэффициента при 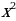 многочлена второй степени. Это уравнение нельзя сразу решить по формулам для отыскания корней квадратного уравнения, т.к. о заданном уравнении мы не можем сказать, квадратное оно или линейное)
многочлена второй степени. Это уравнение нельзя сразу решить по формулам для отыскания корней квадратного уравнения, т.к. о заданном уравнении мы не можем сказать, квадратное оно или линейное)
| ! | Если коэффициент при 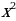 многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль |
Решим уравнение (2) 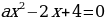
Решение. Рассмотрим два случая, когда 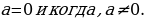
-
При 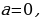 уравнение линейное
уравнение линейное 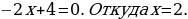
-
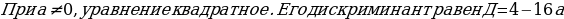
-
Если Д , уравнение решений не имеет.
-
Если Д=0, т.е. 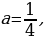 то уравнение имеет один единственный корень
то уравнение имеет один единственный корень 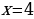
-
Если Д0,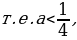 то уравнение имеет два корня
то уравнение имеет два корня 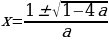
Ответ:
если 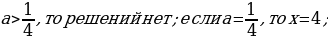
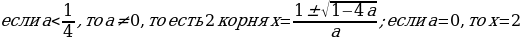
Этап III
Цель: повторить понятие равносильности и алгоритм решения рационального уравнения
| ! | Два уравнения называются равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней
(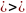 |
| ! | Уравнение (2) называется следствием уравнения (1), если любой корень уравнения (1) является корнем уравнения (2) 
|
Задание 1
Может ли нарушиться равносильность, если выполнить следующие преобразование:
| 1. | В уравнении 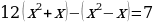 раскрыть скобки и привести подобные члены раскрыть скобки и привести подобные члены |
| 2. | В уравнении 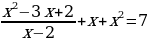 дробь дробь  сократить на сократить на 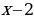 |
| 3. | Обе части уравнения 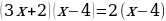 разделить на разделить на 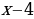 |
| 4. | В уравнении 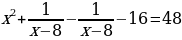 разность разность 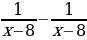 заменить нулем заменить нулем |
| 5. | Обе части уравнения  |
Ответ: Нет(1).Да(2).Да(3).Да(4).Нет(5).
Задание 2
Объяснить, какое преобразование было выполнено при переходе от первого уравнения ко второму и может ли оно привести к нарушению равносильности.
Используя знаки 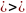 (знак логического следования) и
(знак логического следования) и 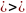 (знак равносильности), покажите равносильные уравнения и уравнения следствия.
(знак равносильности), покажите равносильные уравнения и уравнения следствия.
| № | 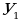
| Знак | 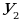
|
| 1. | 2. | 3. | 4. |
| 1. | 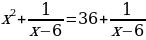
| 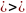
| 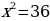
|
| 2. | 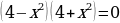
| 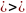
| 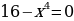
|
| 3. | 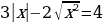
| 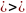
| 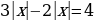
|
| 4. | 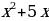 +4=0 +4=0
| 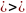
| 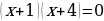
|
| 5. | 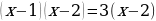
| 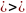
| 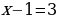
|
| 6. | 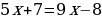
| 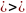
| 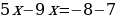
|
| 7. | 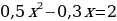
| 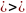
| 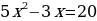
|
| 8. | 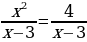
| 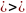
| 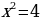
|
Вывод:





Преобразования
Равносильные
Неравносильные
1.Простейшие преобразования(6;7)
2.Преобразования связанные приме-нением тождественных равенств(2;3)
3.Решение простейших уравнений(4)
1.Освобождение от знаменателей, содержащих переменные(8)
2.Приведение подобных членов уравнения(1)
Многие уравнения можно решать как переходом к следствию, так и при помощи равносильных преобразований на множестве.
Задание 3
Решить уравнение 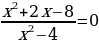 двумя способами.
двумя способами.
Решение.
Способ 1. Применение преобразований, равносильных на множестве (метод равносильных переходов).
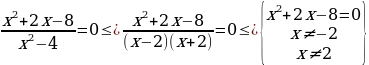
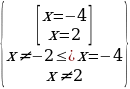
Ответ: -4
Способ 2. Переход к следствию 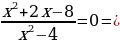
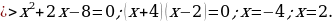
Для найденных значений проверим выполнение условия 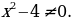
Проверка. 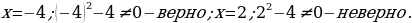
Ответ: -4
Задание «лото» -дифференцированная самостоятельная работа по выбору учащихся (выполнение в парах)
Задание 1. Решить три уравнения, записанные на карте, найти карточки с правильными ответами и закрыть ими соответствующие уравнения. Карточки нужно класть ответом вниз, тогда на верхней их стороне получится ребус.
Задание 2. Разгадать ребус, ответить на вопрос.
-
Какой математик доказал теорему, выражающую связь между коэффициентами квадратного уравнения и его корнями.
-
Что надо искать прежде, чем корни квадратного уравнения?
-
Какой математик однажды заметил что: «Математическую теорию можно считать совершенной только тогда, когда ты сделал ее настолько ясной, что берешься изложить ее содержание первому встречному?»
В той работе оценивается коэффициент участия в решении.
Карта с уравнениями
| I 
| 1. 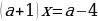
| 2. 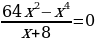
| 3. 
|
|
|
| II 
| 1. 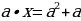
| 2. 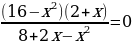
| 3. 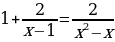
|
|
|
| III 
| 1. 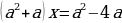
| 2. 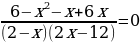
| 3. 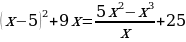
|
Карточки с правильными ответами
| № | 1 | 2 | 3 |
| 1 | 2 | 3 | 4 |
| Ответы | Если 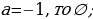 Если 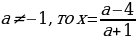 | 0;8 | 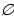
|
| Обратная сторона карточки | (1540-1603.) | 
| 
|
| I | Виет |
| Ответы | Если 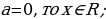 Если 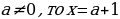 | -4 | -2 |
| Обратная сторона карточки | 
| 
|  |
| I I I | Дискриминант |
| Ответы | При 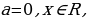 При 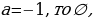 При 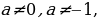 То 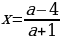
| -1 | 3 |
| Обратная сторона карточки | 
| 
| 
|
| I II II | Гильберт |






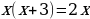
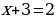
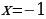
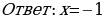
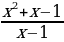 =
=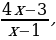
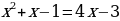 ,
,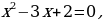
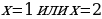 ,
,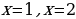
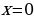 , а в примере 2 появился «посторонний» корень
, а в примере 2 появился «посторонний» корень 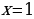 )
)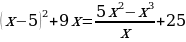
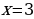
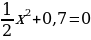 Нет действительных корней(
Нет действительных корней(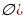
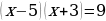
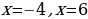
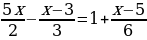
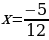
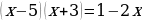
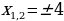
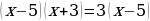
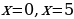
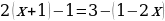 Нет действительных корней
Нет действительных корней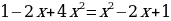 х= 0
х= 0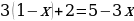 Бесконечное множество корней
Бесконечное множество корней 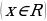
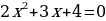 Нет действительных корней(
Нет действительных корней(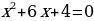

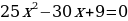
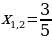


 Ввиды ввв
Ввиды ввв

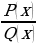 =0,где
=0,где 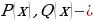 многочлены,
многочлены, 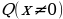 №1
№1


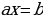 )
)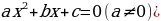

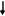



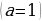
 )
)



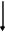




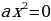
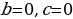
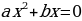
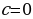
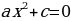
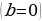
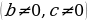

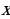 , при которых определены обе части уравнения
, при которых определены обе части уравнения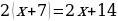
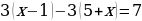
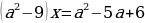
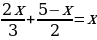
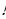
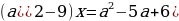
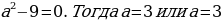 .
.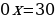 и корней не имеет.
и корней не имеет.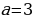 , то получаем уравнение
, то получаем уравнение 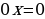 , для которого любое действительное число является корнем.
, для которого любое действительное число является корнем.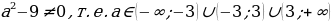
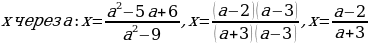
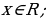
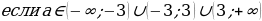 ,то один корень
,то один корень 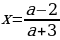

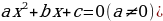




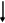

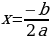
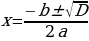







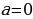
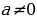
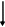
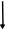

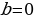
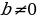


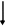

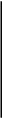



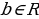

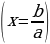
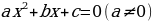 с его дискриминантом
с его дискриминантом 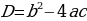 , и для каждого случая аналитического решения указать геометрическую модель.
, и для каждого случая аналитического решения указать геометрическую модель.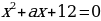
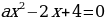
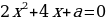
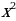 многочлена второй степени. Это уравнение нельзя сразу решить по формулам для отыскания корней квадратного уравнения, т.к. о заданном уравнении мы не можем сказать, квадратное оно или линейное)
многочлена второй степени. Это уравнение нельзя сразу решить по формулам для отыскания корней квадратного уравнения, т.к. о заданном уравнении мы не можем сказать, квадратное оно или линейное)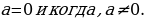
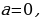 уравнение линейное
уравнение линейное 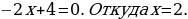
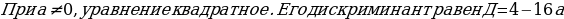
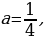 то уравнение имеет один единственный корень
то уравнение имеет один единственный корень 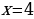
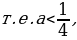 то уравнение имеет два корня
то уравнение имеет два корня 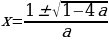
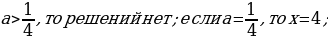
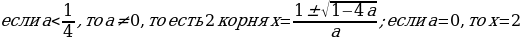
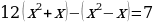 раскрыть скобки и привести подобные члены
раскрыть скобки и привести подобные члены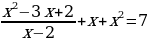 дробь
дробь  сократить на
сократить на 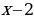
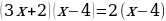 разделить на
разделить на 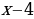
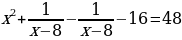 разность
разность 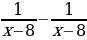 заменить нулем
заменить нулем
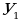
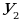
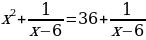
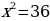
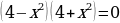
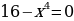
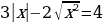
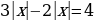
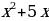 +4=0
+4=0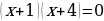
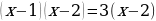
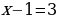
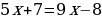
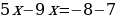
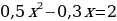
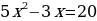
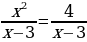
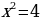





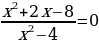 двумя способами.
двумя способами.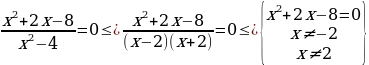
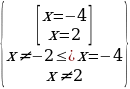
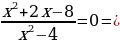
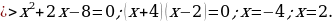
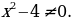
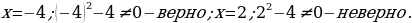

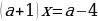
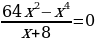


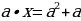
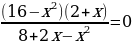
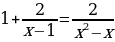

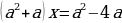
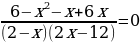
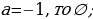
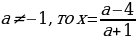



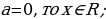
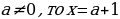



 I
I 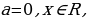
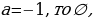
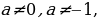
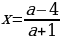

 II
II



















