Открытый урок по теме " Решение задач с помощью дробных рациональных уравнений"

ДА

Ч

«Мне приходится делить время между политикой и уравнением. Однако уравнение, по – моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно»

Альберт Энштейн

Решение задач с помощью ДРОБНО- рациональных уравнений

Повторение

1. Какие из представленных ниже уравнений дробно-рациональные?

Вопрос:

Ответ : 2, 3, 5

Повторение

• Работа в парах. Запишите в тетради общий знаменатель дробей, входящих в уравнение

Ответ :

1) (х+7)(х-4); 2) (х+2)(х-2); 3) (х+3)(х-3); 4) (х-8)(х+8); 5) х(х-7).

Порядок решения рациональных уравнений.  

• Все переносим в левую часть.
• Найти наименьший общий знаменатель дробей, входящих в уравнение.
• Умножить обе части уравнения на общий знаменатель.
• Решить получившееся целое уравнение .

• Из найденных корней исключить те, которые обращают в нуль общий знаменатель данного уравнения.

• Записать ответ

Дробь равна нулю, тогда и только тогда, когда числитель равен нулю , а знаменатель не равен нулю .

Решить уравнение: .

Решение:

Проверка:

При , .

, при .

При , .

Общий знаменатель .

Если среди найденных корней окажется

такое число, при котором знаменатель

дроби обращается в нуль , то такое

число корнем уравнения быть не может ,

его называют посторонним корнем и в

ответ не включают .

или

;

Ответ: .

Этапы решения задачи:

• Составьте математическую модель по условию задачи.
• Выберите нужную формулу из перечисленных:
• ; t
• ;
• ;
• ;

• Масса раствора = + + +…
• Составьте уравнение.
• Решите уравнение и не забудьте про ОДЗ.
• Соотнесите полученный результат с условием задачи.
• Запишите ответ.

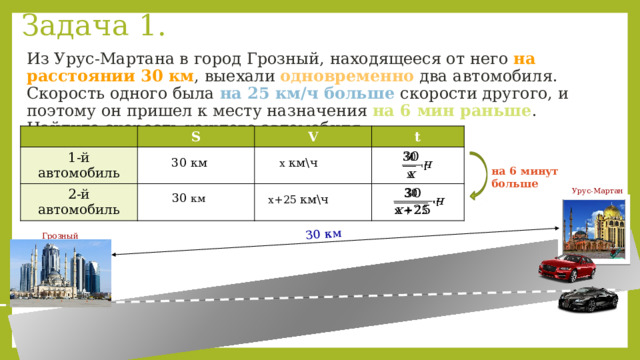
Задача 1.

30 км

Из Урус-Мартана в город Грозный, находящееся от него на расстоянии 30 км , выехали одновременно два автомобиля. Скорость одного была на 25 км/ч больше скорости другого, и поэтому он пришел к месту назначения на 6 мин раньше . Найдите скорость каждого автомобиля.

S

1-й автомобиль

V

2-й автомобиль

t

x км\ч

30 км

на 6 минут больше

Урус-Мартан

30 км

х+25 км\ч

Грозный

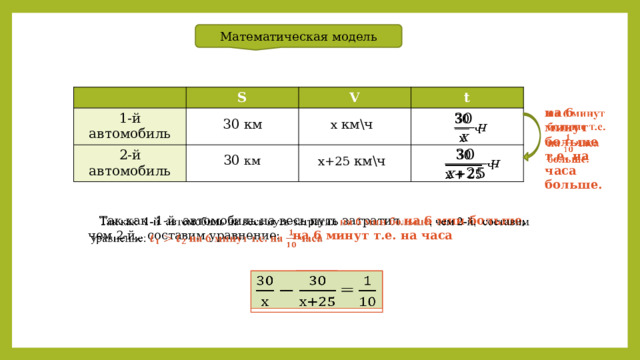
Математическая модель

1-й автомобиль

S

2-й автомобиль

V

t

на 6 минут больше т.е. на часа больше.

x км\ч

30 км

30 км

х+25 км\ч

Так как 1-й автомобиль на весь путь затратил на 6 мин больше , чем 2-й, составим уравнение: на 6 минут т.е. на часа

=

Решение уравнения:

=

Выносим за скобки общий множитель х и 75

х(х+100)

(х+100)

х = 100,

Значит

Не удвл. условию задачи

Ответ: 75 км\ч, 100 км\ч

Задача 2

Расстояние между пристанями А и В равно 135 км . Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 80 км . Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч .

S

Лодка по течению

Лодка против течения

V

Плот

t

X+4 км\ч

135 км

135 км

Х-4 км\ч

4 км\ч

80 км

80:4=20 ч

Составление уравнения:

Время пребывания лодки по воде на 2 часа меньше

Составим уравнение, где время пребывания лодки по воде складывается из времени движения по течению и времени движения против течения и на 2 часа меньше времени движения плота, т.к. лодка выдвинулась позже:

Поскольку скорость не может быть отрицательной величиной, собственная скорость лодки равна 16 км/ч.

Ответ: 16

«Я, МЫ, ДЕЛО»

• Оцените по 10 - бальной шкале
• Я 0_________10 (как чувствовал себя в процессе учения).
• Мы 0_________10 (насколько комфортно мне работалось в паре).
• Дело 0_________10 я достиг цели учения.

Домашнее задание: № 332 (а,б)