Открытый урок погеометрии

Тема урока: Прямоугольная система координат в пространстве.

Цели урока:

• Сформировать понятие системы координат и координаты точки в пространстве; выработать умения строить точку по заданным её координатам; находить координаты точек, изображённой в заданной системе координат;

• Способствовать развитию пространственного воображения учащихся; умение развивать аналогии сравнение; способствовать выработке решения задач и развития логического мышления учащихся.

• Воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.

Ход урока

1. Организационный момент, приветствие, пожелания плодотворной работы.

2. Мотивация урока.

Ребята, чтобы найти конкретного человека на нашей планете, что необходимо нам знать? Правильно его место нахождение, т.е. другими словами мы должны знать его координаты.

Все путешественники должны быть вечно благодарны древнегреческому ученому Гиппарху.

Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо теперь известные географические координаты: широту и долготу – и обозначить их числами.

Во II веке н.э. знаменитый древнегреческий астроном Клавдий Птолемей уже пользовался долготой и широтой в качестве географических координат.

В ХIVв. Французский математик НИКОЛАЙ ОРЕЗМСКИЙ ввел, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой.

Это нововведение оказалось чрезвычайно продуктивным. На его основе возник метод координат, связавший геометрию с алгеброй. Основная заслуга в создании метода координат принадлежит французскому математику Р. Декарту. Как не потеряться в этой жизни? Я думаю нам помогут координаты!!!!

3.Актуализация знаний.

Фронтальный опрос по технологии «Микрофон».

1. Как можно двигаться по прямой?

2. Сколькими координатами может быть задана точка на прямой?

3. В каком направлении можно двигаться на плоскости?

4. Чем определяются точки на координатной плоскости?

5. Что такое координата?

6. Как задать координатную плоскость?

7. Как называется ось 0Х, 0У?

4. Изучение нового материала.

Давайте вместе с вами выясним, как можно двигаться в пространстве? Вверх и вниз, влево и вправо, вперёд и назад. Достаточно ли нам двух координатных осей для определения положения тела в пространстве?Если через точку пространства проведены 3 попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.

Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Она обозначается буквой О. Оси координат обозначаются так: Ох, Оу, Оz. Их называют: ось абсцисс, ось ординат, ось аппликат.

Точка О разделяет каждую из осей координат на 2 луча, один из них – положительная полуось, другой – отрицательная полуось. Вся система обозначается Охуz.

Три плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох - координатные плоскости. Их обозначают Оху, Оуz, Оzх.

В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются её координатами.

Проведем через точку М три плоскости, перпендикулярные к осям координат, и обозначим через М₁, М₂ и М₃, точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат. М₁ – абсцисса, М₂ – ордината, М₃ – аппликата точки М. Координаты точки М записываются: М (х; у; z), х – абсцисса, у – ордината, z-аппликата.

5. Минута отдыха.

Массаж ушных раковин.

Более тысячи биологически активных точек на ухе известно в настоящее время, поэтому, массируя их, можно последовательно воздействовать на весь организм. Нужно стараться так помассировать ушные раковины, чтобы уши «горели». Упражнение можно выполнять в такой последовательности:
1) потягивание за мочки сверху вниз;
2) потягивание ушной раковины вверх;
3) потягивание ушной раковины к наружи;
4) круговые движения ушной раковины по часовой стрелке и против;

5) растирание ушей до ощущения «горения».

6.Закрепление нового материала.

1.Определить координаты точек А, В, С,D, E, F (на карточках). Какие лежат на осях? Какие в координатных плоскостях? Ответы: A (9; 5; 10) ; В (4; -3; 6);

С (9; 0; 0);Д (4; 0; 5); Е (0; 3; 0); F (0; 0; -3)

Вывод оформим в виде блоксхемы

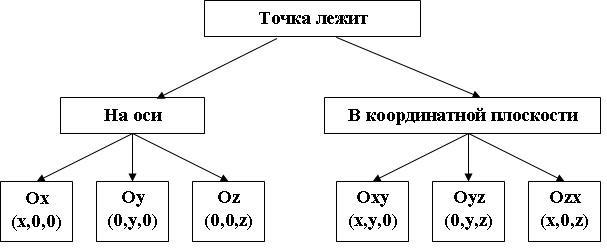
2.По координатам оределите, какие из них лежат на той или иной координатной оси или той или иной координатной плрскости: К (0; 0; -7); Д (2; 0; 0); Т (-4; 0; 3);

Е (0; -1; 0); С (1; 2; 3 ); Р (0; 5; -7); А (-√5; √3; 0 )

Точки, лежащие но осиOx Д

Точки, лежащие но осиOy Е

Точки, лежащие но осиOz К

Точки, лежащие но осиOxy А

Точки, лежащие но осиOyz Р

Точки, лежащие но осиOxz Т

7.

Небылица о случае, который подсказал Декарту идею координат

Однажды в незнакомый город
Приехал молодой Декарт.
Его ужасно мучил голод.
Стоял промозглый месяц март.

Решил к прохожей обратиться
Декарт, пытаясь дрожь унять:
- Где тут гостиница, скажите?
И дама стала объяснять:

- Идите до молочной лавки,
Потом до булочной, за ней
Цыганка продает булавки
И яд для крыс и для мышей,

А дальше будут магазины,
Найдете в них наверняка
Сыры, бисквиты, фрукты, вина
И разноцветные шелка…

Все объясненья эти слушал
Декарт, от холода дрожа.
Ему хотелось очень кушать.
Но звонкий голос продолжал:

- За магазинами – аптека
(аптекарь там – ученый швед),
И церковь, где в начале века
Венчался, кажется, мой дед…

Когда на миг умолкла дама,
Вдруг произнес ее слуга:
- Идите три квартала прямо
И два направо. Вход с угла.

Как вы думаете, удалось ли Декарту найти гостиницу по этому описанию? Возможно именно этот случай подвиг Декарта к созданию прямоугольной системы координат

8.Ну а мы продолжаем.

1. Постройте по координатам точки А (1; 2; 3); В (-2; 0; 3); С (0; 0; -4); Д (3; -1; 0)

(Раздаточный материал-система координат в файле)

2.Найти координаты проекций точки А (2; -3; 5) на каждую из координатных плоскостей и на каждую из координатных осей. Ответы: Аox (2; 0; 0); Aoy (0; -3; 0); Aoz (0; 0; 5); Aoxy (2; -3; 0); Aoyz (0; -3; 5); Aoxz (2; 0; 5)

3. Решаем задачу № 402 стр. 108 (Учебник «Геометрия 10-11 класс» Автор Атанасян Л.С.)

9. Итоги урока. Рефлексия.

Оценивание

1. Нахождение координат

2. Принадлежность точек к координатным осям и координатным плоскостям

3. Нахождение проекций точки на оси и координатные плоскости

4. Задача №402

10. Д/з. карточки в тетради (сделать рисунок по заданным координатам)

1. (2; -1; 0); (2; -1; 1,5); (2; 3; 1,5); (2; 3; 0); (2; -1; 0)

2. (2; -1; 1,5); (2; -1; 2); (2; 3; 2); (2; 3; 1,5);

3. (2; -1; 2); (1; -1; 2); (1; 3; 2); (2; 3; 2)

4. (1; -1; 2); (1; -1; 4); (1; 3; 4); (1; 3; 2)

5. (1; -1; 4); (-5; -1; 4); (-5; 3; 4); (1; 3; 4)

6. (-5; 3; 4); (-5; 3; 0); (2; 3; 0)

7. (-1; 3; 4); (-1; 3; 0)

8. (1; 3; 2); (-1; 3; 2)

9. (0,5; 3; 0); (0,5; 3; 1); (1,5; 3; 1); (1,5; 3; 0)

10. (-2; 3; 0); (-2; 3; 1); (-3; 3; 1); (-3; 3; 0)

11. (-3,5; 3; 0); (-3,5; 3; 1); (-4,5; 3; 1); (-4,5; 3; 0)

12. (0,5; 2; 1,5); (0,5; 1; 2,5)

13. (0; -0,5; 1); (0,5; -1; 2,5)

На уроке познакомились с прямоугольной системой координат в пространстве, научились строить точку по заданным ее координатам и находить координаты точки, изображенной в заданной системе координат. Декартова система координат не единственная. Задание: Найти другие системы координат в пространстве.

Составила:

учитель математики

Антошко Ирина Ивановна

МОУ «Школа №2» города Ждановка