Урок  на тему "Отношение чисел и величин" (6 класс). Учебник Никольский С.М.

ОТНОШЕНИЯ ЧИСЕЛ И ВЕЛИЧИН.

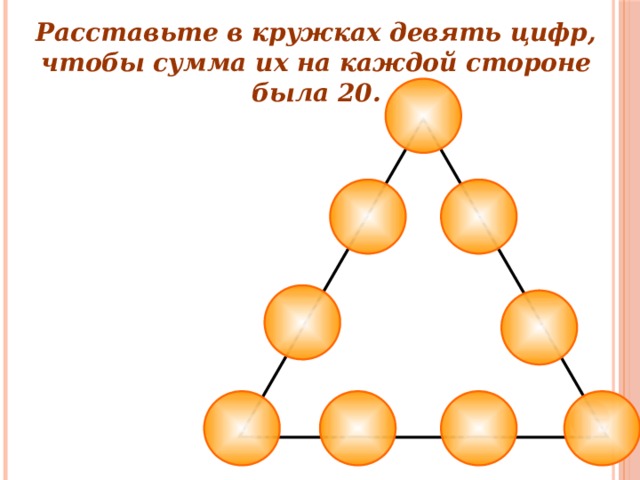
Расставьте в кружках девять цифр, чтобы сумма их на каждой стороне была 20.

Данное задание можно распечатать и раздать каждому ребенку.

ВСПОМНИМ ТЕОРИЮ.

1. Когда говорят, что натуральное число а делится нацело на натуральное число b ?

2. Как называются компоненты при делении?

3. Как найти неизвестное делимое? А делитель?

4. На какие числа делится нацело любое число?

5. Можно ли делить на нуль? А если разделить нуль на любое число?

ВСПОМНИМ ЗАДАЧИ «НА ЧАСТИ».

• Для варенья из малины на 2 части ягод берут 3 части сахара. Сколько сахара необходимо взять на 2 кг 600 г ягод?

=

Ответ: 3 кг 900 г .

2 части

3 части

• Говорят, что ягоды и сахар взяты в отношении 2 к 3.

Записывают: 2 : 3 или .

• Частное двух не равных нулю чисел a и b называют еще отношением чисел a и b .
• Запись: или .
• Читают: « Отношение числа a к числу b» .
• Числа a и b называют членами отношения .

ОПРЕДЕЛЕНИЕ

• Запись: или .
• Читают: «Отношение числа a к числу b» .

Пример 1. Используя слово «отношение», прочитайте запись:

2) ;

1) ;

3) .

Пример 2 . Найдите отношение:

=

=

=

Вспомним основное свойство частного.

Делимое и делитель можно умножить или разделить нацело на одно и то же натуральное число – частное от этого не изменится .

Из основного свойства частного следует свойство отношения.

Отношение не изменится , если его члены умножить или разделить на одно и то же число, не равное нулю.

• Частное двух величин называется отношением этих величин.

• Сами величины называют членами отношения .

• Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число .
• Такие величины называют однородными .
• Пример 3 . Найдите отношение величин:

Отношение однородных величин показывает во сколько раз одна величина больше другой.

• Отношение величин разных наименований: (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина .

Отношение величин в математике.

• Отношение пути (км) к времени (ч) есть новая величина – скорость , выраженная в единицах скорости (км/ч).

Отношение величин в математике .

• Пример 4 . Найдите отношение пути (16 км) ко времени (8 ч):

Какую новую величину получим?

Отношение величин в математике.

• Отношение стоимости товара (р.) к его массе (кг) есть новая величина – цена , выраженная в единицах цены (р./кг).

Знаменатель в единицах цены обычно не пишут, а пишут и говорят «цена 1 кг товара 50 р.».

Отношение величин в математике .

• Пример 5 . Найдите отношение стоимости товара (24 р.) к его массе (8 кг):

Какую новую величину получим?

Отношение величин в физике.

• Отношение массы тела (например, бруса) (кг) к его объему (м 3 ) есть новая величина – плотность вещества , выраженная в единицах плотности (кг/м 3 ).

Отношение величин в физике .

• Пример 6 . Найдите отношение массы бруса (120 кг) к его объёму (40 м 3 ):

Какую новую величину получим?

Отношение величин в химии.

• Отношение массы вещества (например, соли) (кг) к объему раствора (м 3 ) есть новая величина – концентрация раствора , выраженная в единицах концентрации (кг/м 3 ).

Отношение величин в химм .

• Пример 7 . Найдите отношение массы соли (82 кг) к объёму раствора (41 м 3 ) :

Какую новую величину получим?