Оценка погрешности вычисления производных на основе
варьируемой кусочно-полиномиальной аппроксимации функции
Аппроксимация действительной функции
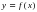
от одной действительной переменной на произвольном отрезке
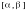
выполняется следующим образом [1 – 3]. Выбирается система подынтервалов равной длины, объединение которых покрывает
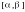
:
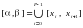 , (1)
, (1)
для определенности полагается 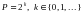 . Пусть априори задана граница
. Пусть априори задана граница  абсолютной погрешности аппроксимации данной функции. При каждом
абсолютной погрешности аппроксимации данной функции. При каждом  из (1) на
из (1) на  -м подынтервале строится интерполяционный полином Ньютона
-м подынтервале строится интерполяционный полином Ньютона 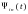 с равноотстоящими узлами, где
с равноотстоящими узлами, где 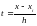 ,
, 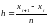 – расстояние между узлами. Степень полинома
– расстояние между узлами. Степень полинома  выбирается одинаковой для всех подынтервалов и минимальной при условии:
выбирается одинаковой для всех подынтервалов и минимальной при условии:
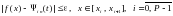 . (2)
. (2)
Интерполяционный полином Ньютона преобразуется к виду:
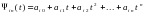 ,
, 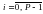 , (3)
, (3)
где 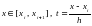 .
.
Искомую оценку выполним в предположении, что 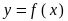 определена, непрерывна и дважды непрерывно дифференцируема на
определена, непрерывна и дважды непрерывно дифференцируема на 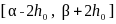 , на концах подразумеваются соответственные односторонние производные. В предположении разбиения (1) и аппроксимации (2) на
, на концах подразумеваются соответственные односторонние производные. В предположении разбиения (1) и аппроксимации (2) на 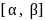 для
для 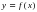 , в предположении
, в предположении 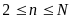 , при произвольно фиксированном
, при произвольно фиксированном 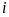 разложим разность
разложим разность 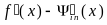 по формуле Тейлора с двумя членами в окрестности радиуса
по формуле Тейлора с двумя членами в окрестности радиуса 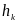 произвольно выбранного узла интерполяции на
произвольно выбранного узла интерполяции на 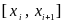 :
:
.
Отсюда для  выполнено:
выполнено:
, (4)
где  .
.
В данных предположениях
 .
.
Иными словами,
 .
.
где .
Покажем, что
.
Имеем:
,
или,
Покажем вначале ограниченность слагаемого, содержащего . По лемме П1.1, представленной в [4], полиномограничен значением. По определению, , далее,
Отсюда
Аналогично,
где . Почленное вычитание обеих частей двух последних равенств влечет:
По формуле Лагранжа, применительно к приращениям производных с величиной приращения аргумента , получится:
где  . Отсюда
. Отсюда
где . Из последнего выражения для в [4] выводится неравенство:
.
С учетом суммы биномиальных коэффициентов оценка примет вид:
.
Аналогично предыдущему, по индукции можно показать ограниченность конечных разностей, а значит и ограниченность всех коэффициентов полинома , а соответственно и всех его производных.
, а соответственно и всех его производных.
Подстановка найденных оценок в выражение второй производной интерполяционного полинома влечет:
или
.
Отсюда
,
где  – постоянная. Поэтому
– постоянная. Поэтому
.
Окончательно, с добавлением единичных слагаемых под знаком суммы,
.
Отсюда следует, что
.
Из данных оценок получается, что
где  . Таким образом, имеет место неравенство:
. Таким образом, имеет место неравенство:
. (5)
Первое слагаемое в правой части (5) можно оценить, используя формулу Тейлора для  в
в 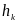 -окрестности узла интерполяции:
-окрестности узла интерполяции:
По условиям интерполяции , поэтому
.
Отсюда
.
В результате последнее неравенство примет вид оценки:
. (6)
Подстановка (6) в выражение разности производных влечет:
. (7)
Таким образом, в предположении о двукратной дифференцируемости функции не удается доказать сходимость и оценить погрешность приближения производной на основе варьируемого кусочно-полиномиального метода.
Выход заключается в том, чтобы предположить более высокий порядок дифференцируемости аппроксимируемой функции. Если функция  непрерывна и непрерывно дифференцируема
непрерывна и непрерывно дифференцируема  раз на отрезке
раз на отрезке 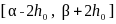 , то для нее сохраняются все проделанные рассуждения и оценки, но кроме того выполняются условия леммы 1.1 из [4]:
, то для нее сохраняются все проделанные рассуждения и оценки, но кроме того выполняются условия леммы 1.1 из [4]:
Лемма. Пусть для произвольного  функция
функция 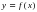 определена, непрерывна и непрерывно дифференцируема
определена, непрерывна и непрерывно дифференцируема  раз на отрезке
раз на отрезке 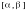 , на концах которого подразумеваются соответственные односторонние производные. Тогда, каково бы ни было
, на концах которого подразумеваются соответственные односторонние производные. Тогда, каково бы ни было  , последовательность полиномов
, последовательность полиномов 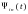 равномерно сходится к функции
равномерно сходится к функции  на данном отрезке при
на данном отрезке при  , где
, где  ,
,  – число подынтервалов из (1). Скорость сходимости оценивается из соотношения
– число подынтервалов из (1). Скорость сходимости оценивается из соотношения
 ,
,  ,
,  ,
,
где  ,
,  – шаг интерполирования полинома
– шаг интерполирования полинома  на
на 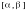 при
при  .
.
В силу леммы для рассматриваемой функции на рассматриваемом отрезке имеет место неравенство:
,, ,
где  .
.
Отсюда
,
где  . Следовательно,
. Следовательно,
,
где .
На основании изложенного приходим к неравенству:
,
 – шаг интерполирования полинома
– шаг интерполирования полинома  на
на  , или,
, или,
.
Таким образом, имеет место
Теорема . Пусть для произвольного функция  определена, непрерывна и непрерывно дифференцируема
определена, непрерывна и непрерывно дифференцируема  раз на отрезке
раз на отрезке 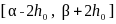 , на концах которого подразумеваются соответственные односторонние производные. Тогда, каково бы ни было
, на концах которого подразумеваются соответственные односторонние производные. Тогда, каково бы ни было  , последовательность полиномов
, последовательность полиномов  равномерно сходится к производной функции
равномерно сходится к производной функции  на отрезке
на отрезке  при
при  , где
, где  ,
,  – число подынтервалов из (1). Скорость сходимости оценивается из соотношения
– число подынтервалов из (1). Скорость сходимости оценивается из соотношения
,

 .
.
С учетом  из теоремы вытекает
из теоремы вытекает
Следствие В условиях теоремы выполняется неравенство
,
при этом  не зависит от выбора степени полинома
не зависит от выбора степени полинома  .
.
Таким образом, если с помощью варьируемого кусочно-полиномиального метода в условиях двукратной дифференцируемости приближается функция, то автоматически приближается производная, причем с равномерной сходимостью при дополнительном требовании  -кратной дифференцируемости приближаемой функции. Скорость сходимости имеет порядок геометрической прогрессии по числу подынтервалов.
-кратной дифференцируемости приближаемой функции. Скорость сходимости имеет порядок геометрической прогрессии по числу подынтервалов.
Литература
Ромм Я. Е. Бесконфликтные и устойчивые методы детерминированной параллельной обработки: автореф. дисс. … д-ра техн. наук. – Таганрог: ТРТУ. – 1998. – 42 с.
Ромм Я. Е. Минимизация временной сложности вычисления функций с приложением к цифровой обработке сигналов: учеб. пособие / Я. Е. Ромм, С. А. Фирсова. – Таганрог: Изд-во Таганрог. гос. пед. ин-та, 2008. – 124 с.
Аксайская Л. Н. Разработка и исследование параллельных схем цифровой обработки сигналов на основе минимизации временной сложности вычисления функций: автореф. дисс. … канд. техн. наук. – Таганрог: ЮФУ, 2008, 18 с.
Ромм Я.Е., Джанунц Г.А. Кусочно-полиномиальные приближения функций и решений дифференциальных уравнений в применении к моделям периодических реакций. – Изд-во ФГБОУ ВПО «ТГПИ имени А.П. Чехова», Таганрог, 2013. – 240 с.







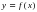 от одной действительной переменной на произвольном отрезке
от одной действительной переменной на произвольном отрезке 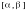 выполняется следующим образом [1 – 3]. Выбирается система подынтервалов равной длины, объединение которых покрывает
выполняется следующим образом [1 – 3]. Выбирается система подынтервалов равной длины, объединение которых покрывает 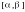 :
: 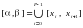 , (1)
, (1)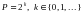 . Пусть априори задана граница
. Пусть априори задана граница  абсолютной погрешности аппроксимации данной функции. При каждом
абсолютной погрешности аппроксимации данной функции. При каждом  из (1) на
из (1) на 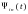 с равноотстоящими узлами, где
с равноотстоящими узлами, где 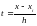 ,
, 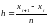 – расстояние между узлами. Степень полинома
– расстояние между узлами. Степень полинома  выбирается одинаковой для всех подынтервалов и минимальной при условии:
выбирается одинаковой для всех подынтервалов и минимальной при условии: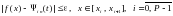 . (2)
. (2)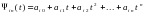 ,
, 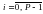 , (3)
, (3)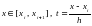 .
.









