государственное автономное профессиональное образовательное учреждение Свердловской области «Нижнетагильский государственный профессиональный колледж имени Никиты Акинфиевича Демидова»
(ГАПОУ СО «НТГПК им. Н.А. Демидова»)
| СОГЛАСОВАНО Председатель ПЦК __________ Я.О. Полякова «___»__________________ | УТВЕРЖДАЮ Зам. директора по УМР __________О.А.Фищукова «___»__________________
|
Пакет контрольно-измерительных материалов для итоговой формы аттестации (в форме экзамена) по дисциплине
«Дискретная математика»
для студентов очного отделения специальности
09.02.05 Прикладная информатика (по отраслям)
Разработчик: Л.М. Авсеенко
г. Нижний Тагил
2017г.
Пояснительная записка
Программа промежуточной аттестации разработана по учебной дисциплине «Дискретная математика», принадлежащей к циклу математических и общих естественнонаучных дисциплин, для обучающихся по специальности 09.05.02 «Прикладная информатика (по отраслям)».
Форма проведения экзамена – ответы на теоретические вопросы и выполнение практических заданий.
Цель промежуточной аттестации: оценка у обучающихся уровня сформированности общих и профессиональных компетенций, складывающихся из соответствующих знаний и умений по дисциплине «Дискретная математика»
уметь:
применять методы дискретной математики;
строить таблицы истинности для формул логики;
представлять булевы функции в виде формул заданного типа;
выполнять операции над множествами, применять аппарат теории множеств для решения задач;
выполнять операции над предикатами;
исследовать бинарные отношения на заданные свойства;
выполнять операции над отображениями и подстановками;
выполнять операции в алгебре вычетов;
применять простейшие криптографические шифры для шифрования текстов;
генерировать основные комбинаторные объекты;
находить характеристики графов;
В результате освоения дисциплины обучающийся должен знать:
логические операции, формулы логики, законы алгебры логики;
основные классы функций, полноту множеств функций, теорему Поста;
основные понятия теории множеств, теоретико-множественные операции и их связь с логическими операциями;
логику предикатов, бинарные отношения и их виды;
элементы теории отображений и алгебры подстановок;
основы алгебры вычетов и их приложение к простейшим криптографическим шифрам;
метод математической индукции;
алгоритмическое перечисление основных комбинаторных объектов;
основы теории графов;
элементы теории автоматов.
Оценка за экзамен определяется по результатам ответа на теоретический вопрос и выполнения пяти практических заданий, равноценных по уровню сложности. Подготовка к ответу на вопрос и выполнение практических заданий рассчитана на 120 минут. Отметка за экзамен выставляется как интегрированная за устный ответ и за практическую работу.
Критерии оценивания устного ответа на экзамене
Оценка «5» («отлично») соответствует следующей качественной характеристике: «изложено правильное понимание вопроса и дан исчерпывающий на него ответ, содержание раскрыто полно, профессионально, грамотно». Выставляется студенту
усвоившему взаимосвязь основных понятий дисциплины в их значении для приобретаемой профессии, проявившему творческие способности в понимании, изложении и использовании учебно-программного материала;
обнаружившему всестороннее систематическое знание учебно-программного материала, четко и самостоятельно (без наводящих вопросов) отвечающему на вопрос билета.
Оценка «4» («хорошо») соответствует следующей качественной характеристике: «изложено правильное понимание вопроса, дано достаточно подробное описание предмета ответа, приведены и раскрыты в тезисной форме основные понятия, относящиеся к предмету ответа, ошибочных положений нет». Выставляется студенту,
обнаружившему полное знание учебно-программного материала, грамотно и по существу отвечающему на вопрос билета и не допускающему при этом существенных неточностей;
показавшему систематический характер знаний по дисциплине и способному к их самостоятельному пополнению и обновлению в ходе дальнейшей учебы и профессиональной деятельности.
Оценка «3» («удовлетворительно») выставляется студенту,
обнаружившему знание основного учебно-программного материала в объеме, необходимом для дальнейшей учебы и предстоящей работы по профессии, справляющемуся с выполнением заданий, предусмотренных программой;
допустившему неточности в ответе и при выполнении экзаменационных заданий, но обладающими необходимыми знаниями для их устранения под руководством преподавателя.
Оценка «2» («неудовлетворительно») выставляется студенту,
обнаружившему существенные пробелы в знаниях основного учебно-программного материала, допустившему принципиальные ошибки в выполнении предусмотренных программой заданий;
давшему ответ, который не соответствует вопросу экзаменационного билета.
Практическая работа, состоящая из пяти равноценных заданий, оценивается по количеству выполненных заданий
Максимальное количество баллов – 15. Итоговая оценка выставляется в соответствии со шкалой: 15-12 баллов – отлично; 11-9 баллов – хорошо; 8-7 баллов – удовлетворительно; 6 и менее баллов – неудовлетворительно. Подведение итогов экзамена и выставление итоговой оценки осуществляется в оценочном листе. Текущая успеваемость и результаты внеаудиторной самостоятельной работы оцениваются от 0 до 5 баллов.
СОДЕРЖАНИЕ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО УЧЕБНОЙ ДИСЦИПЛИНЕ «ДИСКРЕТНАЯ МАТЕМАТИКА»
Вопросы теоретической части
Предмет дискретной математики. Множества, способы их задания. Операции над множествами. Диаграммы Вена. Примеры.
Отношения на множествах. Унарные и бинарные отношения. Основные свойства бинарных отношений. Примеры.
Отношения эквивалентности и порядка на множествах. Примеры.
Булевы функции, табличное их задание, задание в векторной форме. Число БФ от n переменных.
Существенность переменных БФ. Критерий существенности. Равенство БФ. Примеры.
Аналитическое представление БФ, операция суперпозиции. Представимость над множеством БФ.
Понятие логической формулы. Строгое определение класса ЛФ на языке БНФ.
Понятие о СДНФ и СКНФ. Разложение функции в СДНФ.
Понятие о полноте классов БФ. Примеры полных и неполных классов. Полнота класса {or, and, not}.
Теорема о сводимости и её применение для доказательства полноты систем {not, or}, {not, and}, {0, -}.
Полнота системы {+, ., 1}. Разложение БФ в полином Жегалкина.
Леммы о несамодвойственной (с доказательством) и о немонотонной функциях.
Лемма о нелинейной БФ (с доказательством).
Теорема Поста о полноте. Доказательство необходимого условия. Применение теоремы.
Теорема Поста о полноте. Доказательство достаточного условия. Предполные классы.
Понятие о релейно-контактных схемах. РКС -реализация функциональных элементов. Примеры.
Понятие о графах и орграфах. Смежность (вершин, рёбер), инцидентность (вершин и рёбер). Степени вершин. Маршруты, цепи, простые цепи, циклы. Примеры.
Матрицы смежностей и их реализация в языках программирования. Примеры.
Компьютерное представление графов списками смежностей. Примеры.
Подграфы. Изоморфизм и гомеоморфизм графов. Примеры.
Планарность графов.
Связность графов и орграфов – определения, примеры. Компоненты связности.
Алгоритм обхода связного графа. Две основные стратегии обхода.
Алгоритм выявления компонент связности графа.
Деревья, корневые деревья. Бинарное кодирование корневых деревьев. БНФ-определение класса бинарных кодов корневых деревьев.
Практические задания
Дан граф:
Определите вид графа, степень вершин графа, постройте матрицу смежности, кратчайший путь из вершины x1 до x6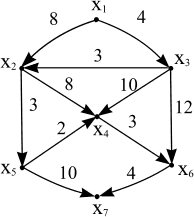
Решить задачу, используя диаграмму Эйлера-Венна.
Четырнадцать спортсменов участвовали в кроссе, 16 – в соревнованиях по плаванью, 10 – в велосипедных гонках. Восемь участников участвовали в кроссе и заплыве, 4 – в кроссе и велосипедных гонках, 9 – в плавании и велосипедных гонках. Во всех трех соревнованиях участвовали три человека. Сколько всего было спортсменов?
Задано универсальное множество U ={1, 2, 3, 4, 5, 6, 7, 8} и множества X={1, 3, 6, 7}, Y = {3, 4, 7, 8}, Z = {3, 4, 7, 8}. Построить булеан множества Х и любое разбиение множества Z.
Даны множества: А = {4, 5, 6}, В = {2, 4, 6}. Найти: А \ В ,В \ А, А + В
Перечислить подмножества следующих множеств:а) {{1, 2}, {3}, 4}; б) {{5, 2}}; в) {{2}, {6}, {3} }; г) {{4, 6}, {1}, 1}.
Решить задачу: Оказалось, что в группе туристов 15 человек были раньше во Франции, 19 в Италии, 8 в Германии. 9 туристов были во Франции и в Италии, 7 во Франции и в Германии, 6 и в Италии, и в Германии. 4 туриста были во всех трех странах. Сколько туристов были хотя бы в одной из трех стран?
Укажите, в каких случаях высказывание истинно, а в каких ложно: 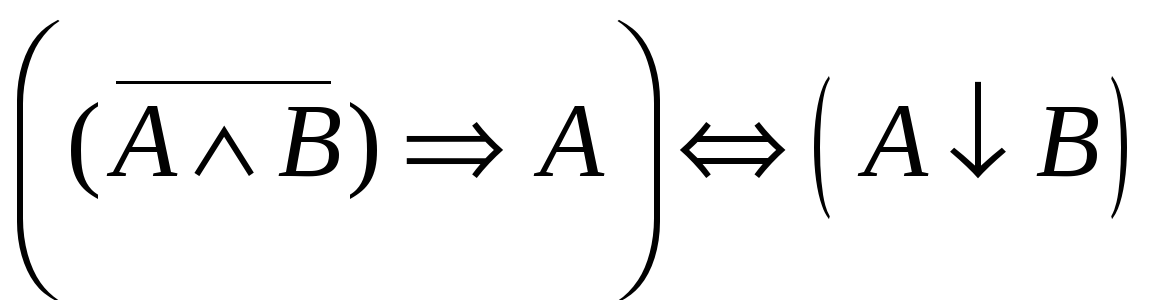
Являются ли эквивалентными следующие высказывания:  и
и 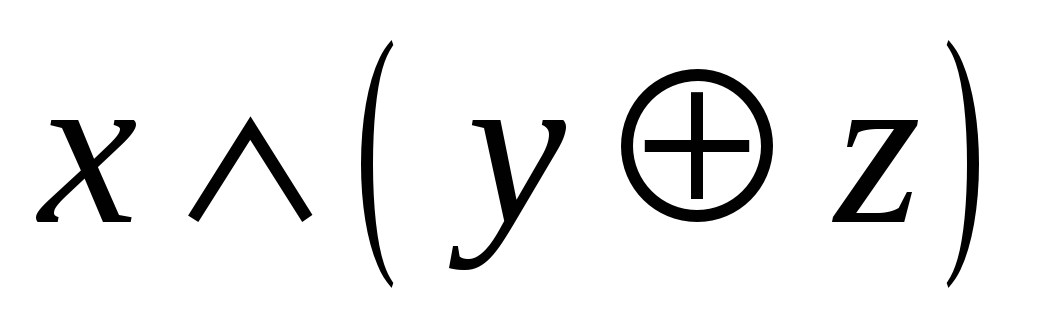
Построить таблицу истинности, найти СНДФ, найти минимальную ДНФ. для высказывания: 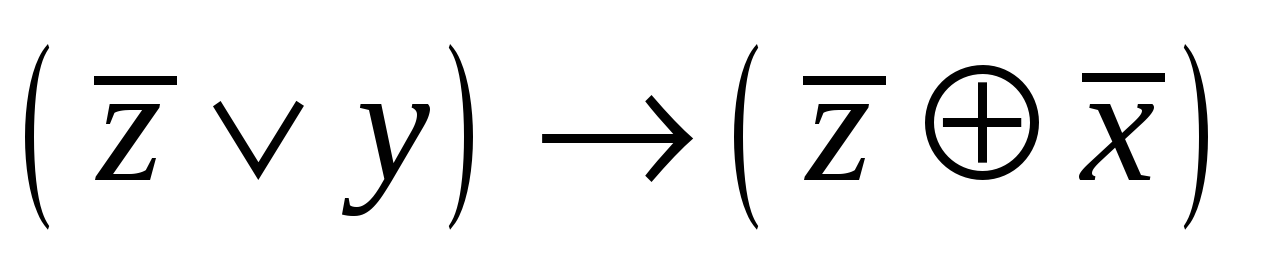
Решить задачу: Аня, Вика и Сергей решили пойти в кино. Учитель, хорошо знавший ребят, высказал предложения: Аня пойдет в кино только тогда, когда пойдут Вика и Сергей; Аня и Сергей пойдут в кино вместе или же оба останутся дома; чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика. Когда ребята пошли в кино, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из ребят пошел в кино?
Найти 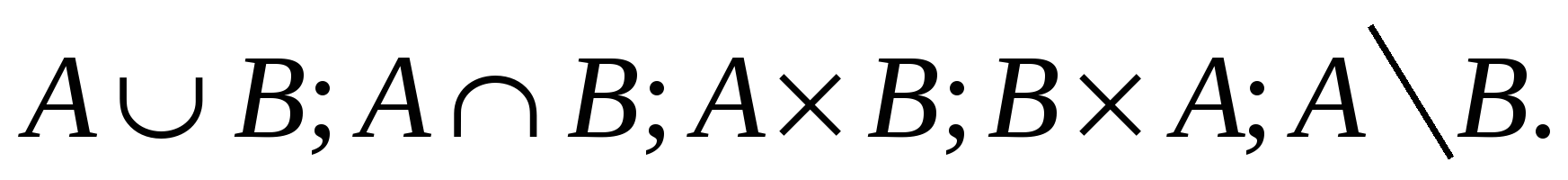
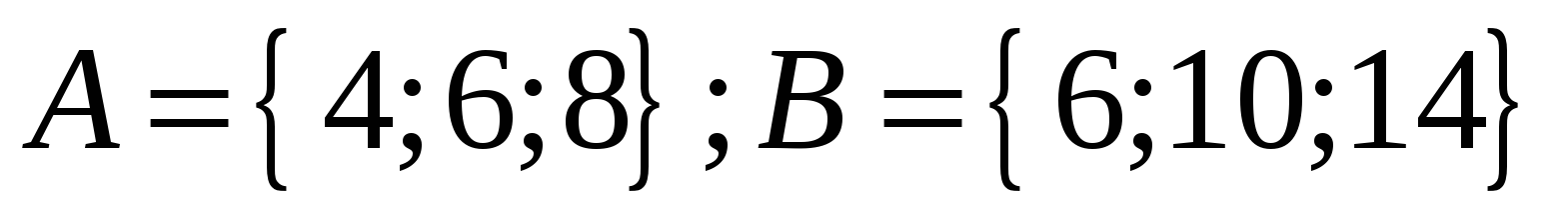
Даны множества M, P, T. Каким будет множество  , если
, если 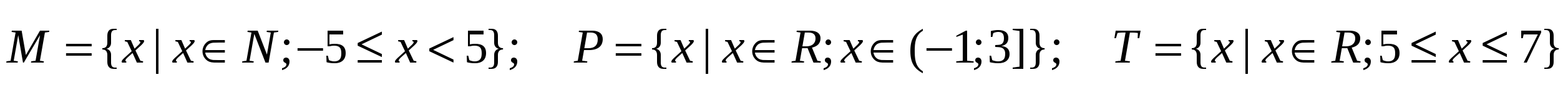
Проверить правильность формул, используя таблицы истинности:  =
= ;
; 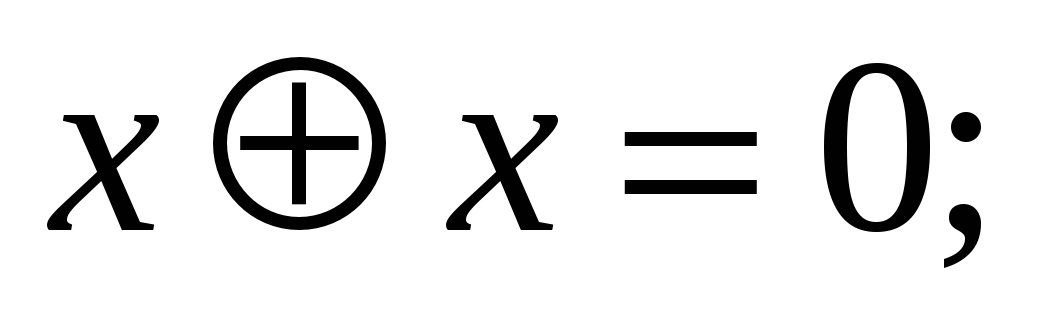
 ;
;  ;
; 
 ;
;  .
.
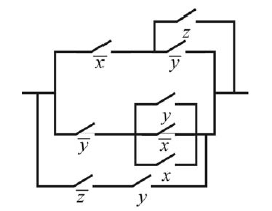
Записать формулу алгебры логики, соответствующую данной релейно-контактной схеме, упростить ее, если это возможно и нарисовать новую схему по упрощенной формуле.
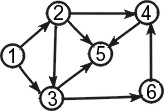
Построить матрицы смежности, инцидентности, достижимости, сильной связности графа G.
ОЦЕНОЧНЫЙ ЛИСТ
|
№ |
Критерии оценки
ФИО студента | УСТНЫЙ ОТВЕТ | ПРАКТИЧЕСКОЕ ЗАДАНИЕ | ВСР | Итого (max= 15 баллов) |
Оценка* |
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
| 10 |
|
|
|
|
|
|
| 11 |
|
|
|
|
|
|
| 12 |
|
|
|
|
|
|
*Оценка по каждому заданию определяется после проверки работы преподавателем. Текущая успеваемость и результаты ВСР оцениваются: 0-5 баллов. Итоговая оценка - по алгоритму: 15-12 баллов – «Отлично», 11-9 балла – «Хорошо», 8-7 баллов – «Удовлетворительно», ≤ 6 баллов – «Неудовлетворительно».
ИНФОРМАЦИОННО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
ОСНОВНЫЕ ИСТОЧНИКИ:
Алексеев В.Е. Графы и алгоритмы. Структуры данных. Модели вычислений: Учебник – М.: Интернет-Университет Информационных Технологий; БИНОМ. Лаборатория Знаний, 2006.
Жильцова Л.П., Смирнова Т.Г. Основы теории графов и теории кодирования в примерах и задачах: Учебное пособие. – Нижний Новгород: ННГУ им. Н.И.Лобачевского, 2008.
Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов: учеб.пособие для студ. высш. учеб. заведений – 4-е изд., стер. – М.:Издательский центр «Академия», 2008.
Игошин В.И. Математическая логика и теория алгоритмов: учеб.пособие для студ.высш. учеб. заведений – 3-е изд., стер. – М.: Издательский центр «Академия», 2008.
Костюкова Н.И. Графы и их применение. Комбинаторные алгоритмы для программистов: Учебное пособие – М.: Интернет-Университет Информационных Технологий; БИНОМ. Лаборатория Знаний, 2007.
Решение задач по статистике, комбинаторике и теории вероятностей. 7-9 классы. /авт.-сост. В. Н. Студенецкая. – Волгоград: Учитель, 2006.
Спирина М.С. Дискретная математика: учебник для студ. учреждений сред. проф.образования – 6-е изд, стер. – М.: Издательский центр «Академия», 2010.
Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. –СПб.: БХВ-Петербург, 2007.
ДОПОЛНИТЕЛЬНЫЕ ИСТОЧНИКИ:
Акимов О.Е. Дискретная математика: логика, группы, графы. – 2-е изд., доп. – М.:Лаборатория Базовых Знаний, 2003.
Березина Л.Ю. Графы и их применение: пособие для учителей. – М.: Просвещение,1979.
Гончарова Г.А., Мочалин А.А Элементы дискретной математики: Учебное пособие. – М.:ФОРУМ: ИНФРА-М, 2004.
Елисеев Е.М., Елисеев М.Е. Элементы дискретной математики. Учебное пособие. –Арзамас, АГПИим. А. П. Гайдара, 2003.
Иванов Б.Н. Дискретная математика. Алгоритмы и программы: Учеб.пособие. – М.:Лаборатория Базовых Знаний, 2002.
Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2002.
Р. Хаггарти. Дискретная математика для программистов. – М.: Техносфера, 2004.
Редькин .П. Дискретная математика: Курс лекций для студентов-механиков. –СПб.:Издательство «Лань», 2003.
Роганов Е.А. Информатика и математика: Конспект лекций. – М.: МГИУ, 2003.
Романовский И.В. Дискретный анализ. Учебное пособие для студентов, специализирующихся по прикладной математике и информатике. – Издание 2-е, исправленное. – СПб.: Невский диалект, 2000.
Яблонский С.В. Введение в дискретную математику: Учеб. Пособие для вузов. – 4-е изд., стер. – М.: Высшшк.; 2003.
ИНТЕРНЕТ-РЕСУРСЫ:
Московский центр непрерывного математического образования (МЦНМО) [Электронный ресурс]http://www.mccme.ru(дата обращения 10.10.2016)
Exponenta.ru: образовательный математический сайт [Электронный ресурс]http://www.exponenta.ru(дата обращения 10.10.2016)
Дискретная математика: алгоритмы (проект ComputerAlgorithmTutor) [Электронный ресурс]http://rain.ifmo.ru/cat/(дата обращения 10.10.2016)
Математика on-line: справочная информация в помощь студенту [Электронный ресурс]http://www.mathem.h1.ru(дата обращения 10.10.2016)
Математика: Консультационный центр преподавателей и выпускников МГУ[Электронный ресурс]http://school.msu.ru(дата обращения 10.10.2016)




















