Памятка. Пропорции.

Памятка: Пропорции

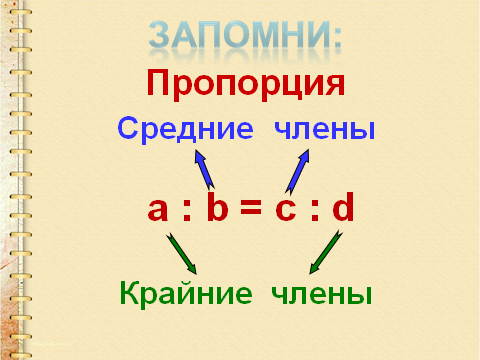
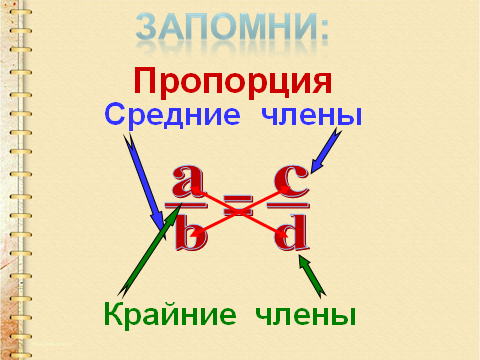
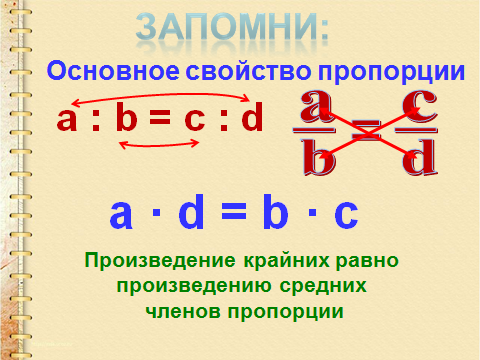
Новые пропорции из основной

В каждой пропорции можно переставить:

• средние члены;

• крайние члены;

• средние и крайние члены;

• крайние на место средних и средние на место крайних

Всего можно получить из данной пропорции 8 пропорций

(включая основную пропорцию)

Упрощение пропорций

Преобразования, не нарушающие пропорцию:

- перестановка членов пропорции:

1) одновременное увеличение/уменьшение обоих членов любого отношения в одинаковое число раз

2) одновременное увеличение/уменьшение обоих предыдущих или обоих последующих членов в одинаковое число раз

3) одновременное увеличение/уменьшение всех членов пропорции в одинаковое число раз

P.S. Если в пропорции средние или крайние члены равны (такие пропорции называют непрерывными),

то из нее можно получить путем перестановки членов только 4 разных пропорций

Производные пропорции a : b = с : d

• Сумма (разность) членов I отношения данной пропорции относится к его последующему члену, как сумма (разность) членов II отношения относится к его последующему

(a+b) : b = (c+d) : d (a-b) : b = (c-d) : d

• Сумма (разность)членов I отношения данной пропорции относится к его предыдущему члену, как сумма (разность) членов II отношения относится к его предыдущему

(a+b) : a = (c+d) : c (a-b) : a = (c-d) : c

• Сумма членов I отношения относится к их разности, как сумма членов II отношения относится к их разности

(a+b) : (a-b) = (c+d) : (c-d)

• Сумма предыдущих членов пропорции относится к сумме последующих, как каждый предыдущий к своему последующему

(a+c) : (b+d) = (a : b) = (c : d)

Все эти и многие другие пропорции, получаемые из данной, называются производными пропорциями

Свойство равных отношений:

если несколько отношений равны друг другу, то сумма всех предыдущих их членов так относится к сумме всех последующих, как каждый предыдущий член - к своему последующему

Из истории пропорций

До XVI века пропорции записывались большей часть словесно или сокращенно. Были сделаны разные попытки введения специального обозначения для пропорций. Так, в одной индийской рукописи XII века пропорция 10 : 163/60 = 4 : 163/150 записывалась следующим образом : 10 163 4 163 1 60 1 150

задачи с пропорциональными величинами раньше назывались, а иногда и теперь - задачами на «тройное правило» (индийского происхождения), т.к в них по трем данным числам находится четвертое пропорциональное.

Тройное правило рассматривается в трудах индийских ученых Ариабхатты, Брахмагупты, Сридддхары, Бхаскары и др.

Средневековые математики ислама, писали справа налево и для записи пропорции применяли троеточие 144.·.84.·.12.·.7 пропорция: 7 : 12 = 84 : 144

В 1631 г. английский математик Вильям Оутред предложил такую запись пропорции: a · b :: c · d

Многие английские математики пользуются этой формой и сейчас.

В 1693 г. саксонский математик Г.В. Лейбниц ввел современную запись пропорции: a : b = с : d