Параллельные прямые

Определение.

Две прямые на плоскости

называются параллельными,

если они не пересекаются.

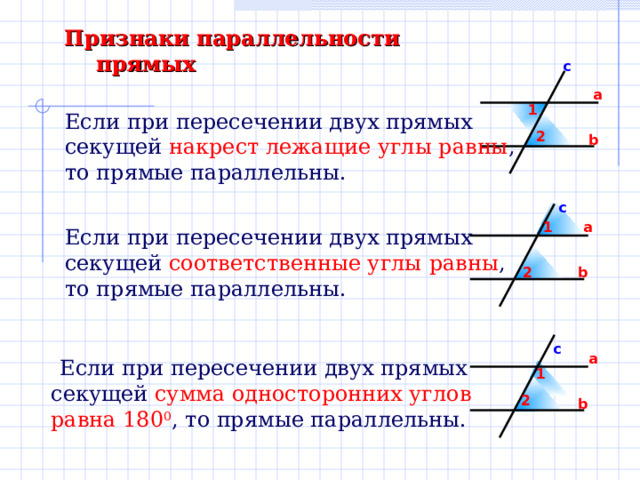
Признаки параллельности прямых

c

а

1

Если при пересечении двух прямых

секущей накрест лежащие углы равны ,

то прямые параллельны.

2

b

c

а

1

Если при пересечении двух прямых

секущей соответственные углы равны ,

то прямые параллельны.

b

2

c

а

Если при пересечении двух прямых секущей сумма односторонних углов равна 180 0 , то прямые параллельны.

1

2

b

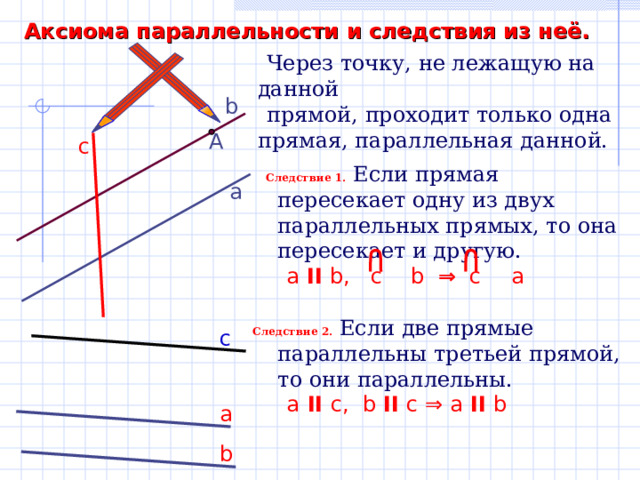
Аксиома параллельности и следствия из неё.

Через точку, не лежащую на данной

прямой, проходит только одна прямая, параллельная данной.

b

А

c

Следствие 1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

a II b , c b ⇒ c a

а

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.

a II с , b II с ⇒ a II b

с

а

b

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Дано: a II b , MN - секущая.

Доказать: 1= 2 (НЛУ)

Доказательство:

способ от противного.

Допустим, что 1 2.

Р

M

а

1

b

2

N

Отложим от луча М N угол N МР, равный углу 2.

По построению накрест лежащие углы N МР= 2

РМ II b .

Получили, что через точку М проходит две прямые (а и МР), параллельные прямой b !!! Это противоречит аксиоме параллельных прямых. Значит наше допущение неверно!!!

1= 2. Теорема доказана.

Теорема об односторонних углах, образованных при пересечении двух параллельных прямых секущей.

две параллельные прямые пересечены секущей,

сумма односторонних углов равна 180 0 .

Если

условие

то

заключение теоремы

c

а

3

Дано: а II b, c- секущая.

Доказать: O У 1 + 2=180 0 .

2

1

b

Доказательство:

3+ 2 =180 0 , т. к. они смежные.

1= 3, т. к. это НЛУ при а II b

3 + 2 =180 0

1

Теорема доказана.

х+30 0

х

х

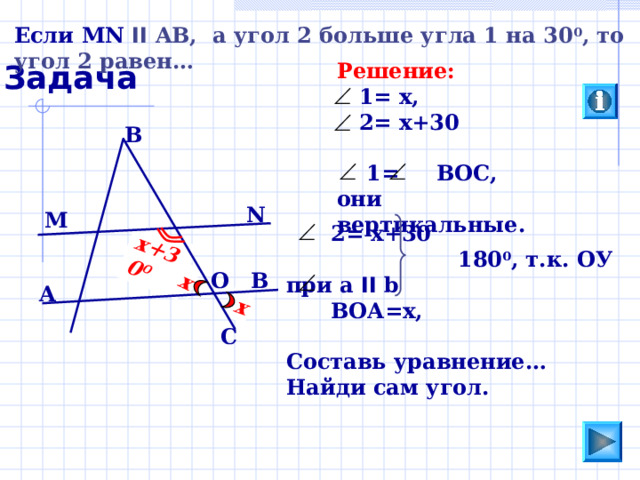
Если MN II AB, а угол 2 больше угла 1 на 30 0 , то угол 2 равен…

Задача

Решение:

1= х,

2= х+30

1= ВОС,

они вертикальные.

В

N

М

2= х+30

180 0 , т.к. ОУ при а II b

ВОА=х,

Составь уравнение…

Найди сам угол.

2

О

B

A

1

B

С

Теорема о соответственных углах, образованных при пересечении двух параллельных прямых секущей.

Если

две параллельные прямые пересечены секущей,

соответственные углы равны.

условие

то

заключение теоремы

c

2

а

Дано: а II b, c- секущая.

Доказать: СУ 1 = 2.

3

b

1

Доказательство:

2 = 3, т. к. они вертикальные.

3 = 1, т. к. это НЛУ при а II b

1

2

1 = 3 = 2

Теорема доказана.

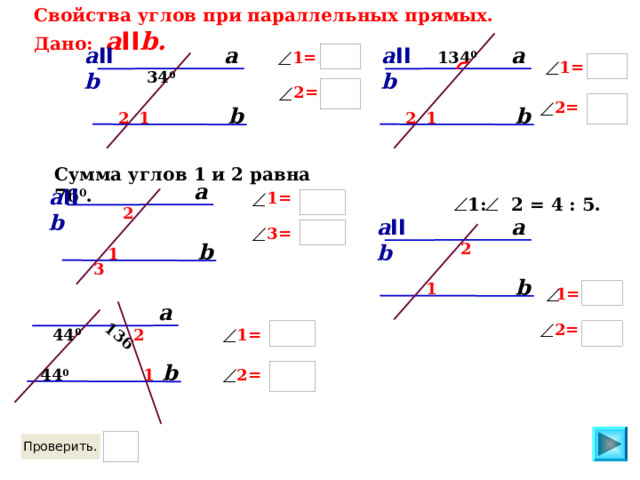
Свойства углов при параллельных прямых. Дано: a II b .

136

a

a

a II b

a II b

1=

1 34 0

1=

34 0

2 =

2 =

b

b

2

2

1

1

Сумма углов 1 и 2 равна 76 0 .

a

a II b

1=

1: 2 = 4 : 5.

2

a

a II b

3 =

2

b

1

3

b

1

1=

a

2 =

2

44 0

1=

b

1

2 =

44 0

Дано: а II b, c – секущая.

Один из односторонних углов на

20% меньше другого.

Найти: все углы.

Задача

c

6

7

а

8

Решение:

2=х,

1 на 20% меньше, т.е. 80%

1=0,8х

2=х

180 0 , т.к. ОУ при 1=0,8х а II b

Составь уравнение…

Найди сам все углы…

2

3

1

b

4

5

5

5=

1=

6=

2=

3=

7=

4=

8=

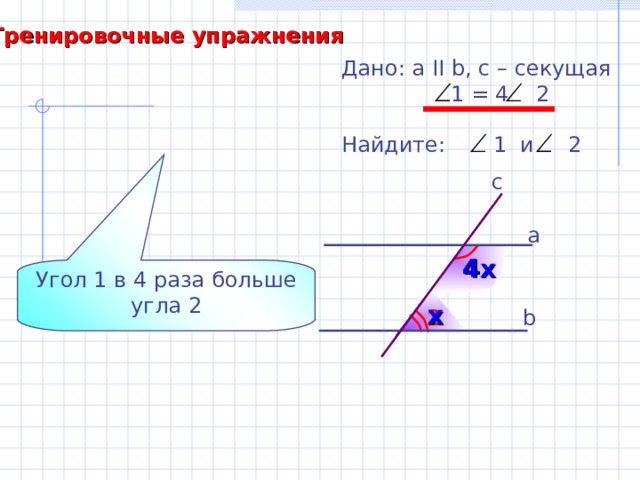
Тренировочные упражнения

Дано: а II b , с – секущая

1 = 4 2

Найдите: 1 и 2

c

а

4х

1

Угол 1 в 4 раза больше угла 2

х

b

2

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

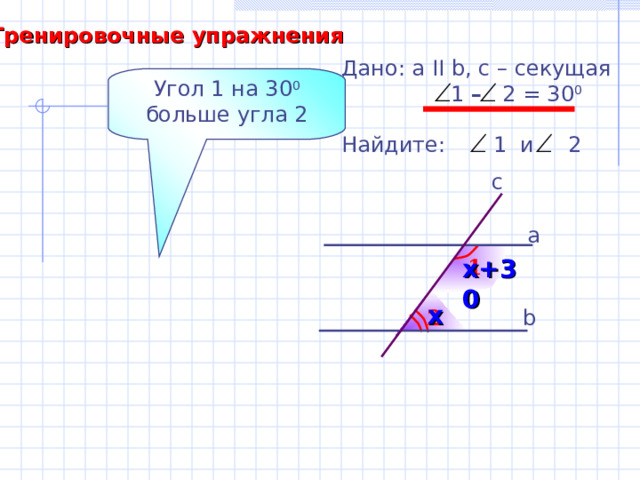
Тренировочные упражнения

Дано: а II b , с – секущая

1 – 2 = 30 0

Найдите: 1 и 2

Угол 1 на 30 0 больше угла 2

c

а

х+30

1

х

b

2

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

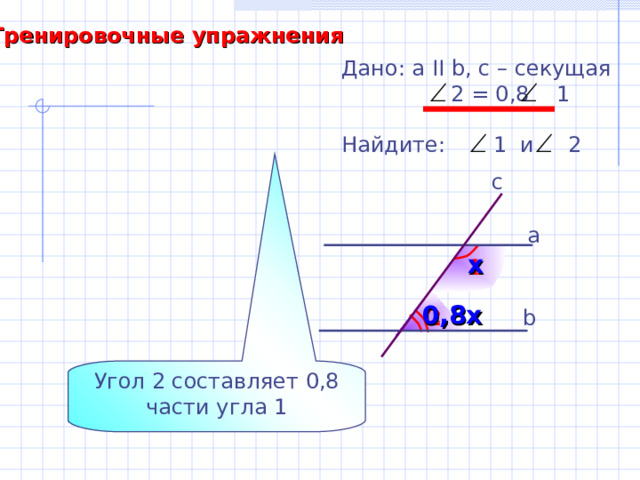
Тренировочные упражнения

Дано: а II b , с – секущая

2 = 0,8 1

Найдите: 1 и 2

c

а

х

1

0,8х

b

2

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах». Как еще можно «расшифровать» условие? Угол 2 составляет 80% угла 1. Угол 2 на 20% меньше угла 1.

Угол 2 составляет 0,8 части угла 1

Тренировочные упражнения

Дано: а II b , с – секущая

1 : 2 = 5 : 4

Найдите: 1 и 2

Пусть х – 1 часть

c

а

5х

1

4х

b

2

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

Тренировочные упражнения

Дано: а II b , с – секущая

2 составляет 80% от 1

Найдите: 1 и 2

c

а

х

1

0,8х

b

2

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

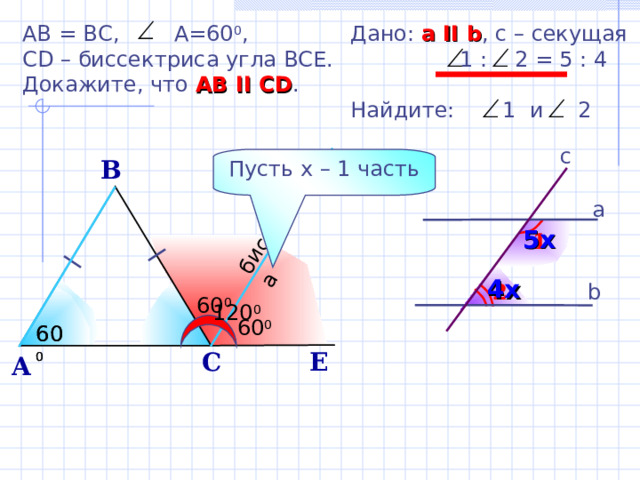
биссектриса

AB = BC, A=60 0 ,

CD – биссектриса угла ВСЕ.

Докажите, что АВ II CD .

Дано: а II b , с – секущая

1 : 2 = 5 : 4

Найдите: 1 и 2

c

Пусть х – 1 часть

B

D

а

5х

1

4х

b

2

120 0

60 0

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

60 0

60 0

60 0

E

С

A

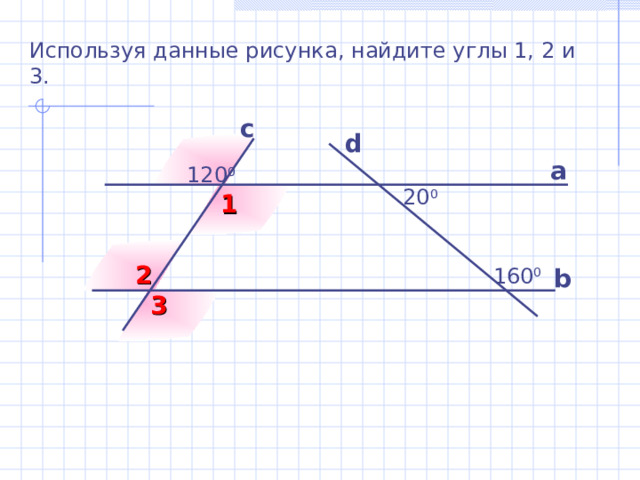
Используя данные рисунка, найдите углы 1, 2 и 3.

с

d

а

120 0

20 0

1

2

160 0

b

3

Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»

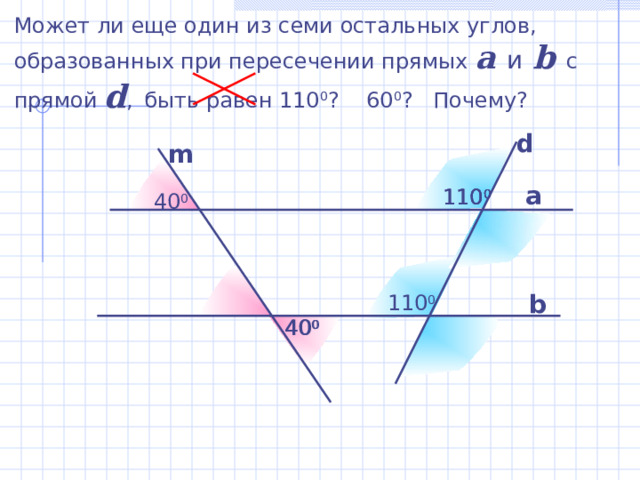
Может ли еще один из семи остальных углов, образованных при пересечении прямых a и b с прямой d , быть равен 110 0 ? 60 0 ? Почему?

d

m

а

11 0 0

11 0 0

11 0 0

4 0 0

b

11 0 0

Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»

4 0 0

4 0 0

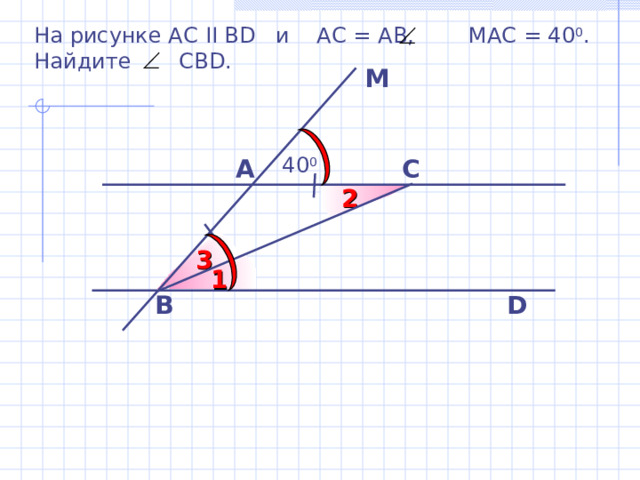
На рисунке АС II В D и АС = АВ, МАС = 40 0 .

Найдите СВ D.

M

40 0

A

С

2

3

1

B

D

Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»

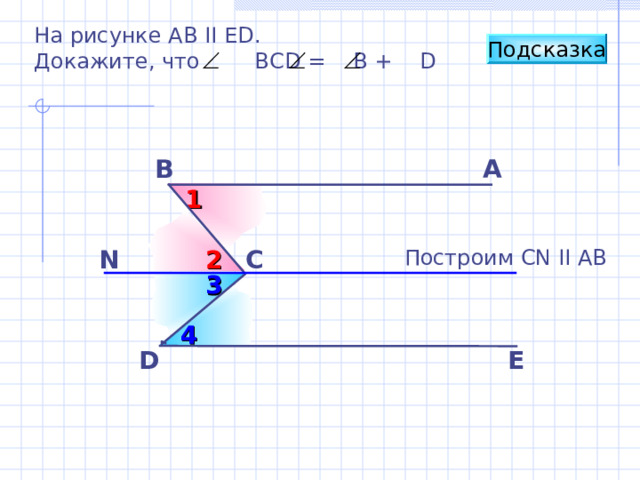
На рисунке АВ II Е D .

Докажите, что ВС D = B + D

Подсказка

A

B

1

N

C

Построим CN II AB

2

3

Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»

4

D

E

На рисунке АВ II Е D . C ВА = 140 0 , С DE = 130 0

Докажите, что ВС С D

Подсказка

B

A

40 0

140 0

N

C

Построим CN II AB

Б.Г. Зив, В.М. Мейлер «Дидактические материалы по геометрии для 7 класса»

130 0

50 0

D

E

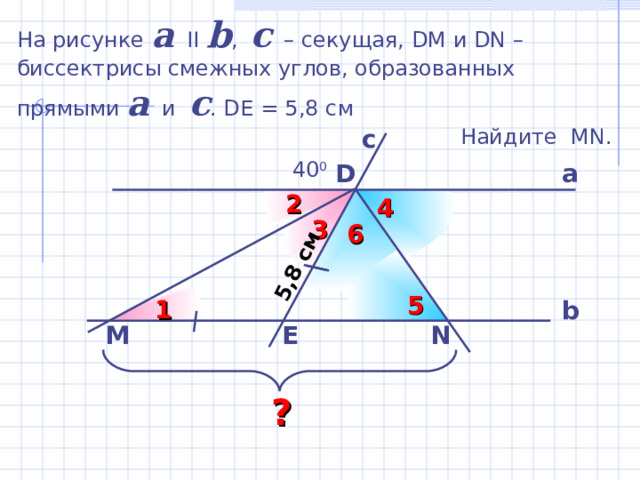
5 ,8 см

На рисунке a II b , c – секущая, DM и DN – биссектрисы смежных углов, образованных прямыми a и c . DE = 5 ,8 см

Найдите MN.

с

40 0

а

D

2

4

3

6

5

1

b

П. И. Алтынов «Геометрия. Тесты. 7-9 кл.»

E

N

M

?

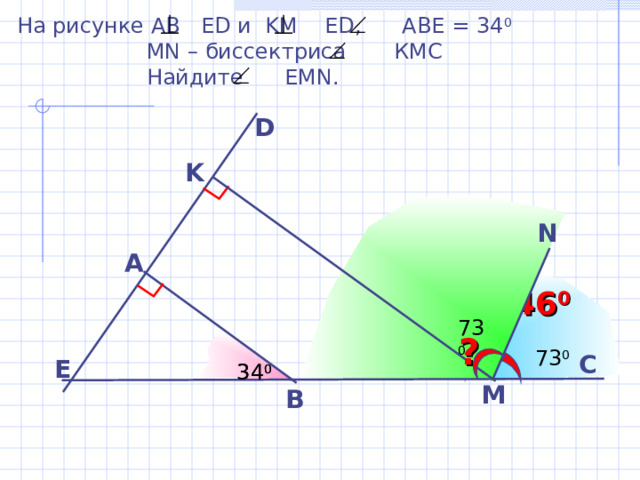
На рисунке АВ ED и KM ED, ABE = 34 0

MN – биссектриса КМС

Найдите EMN.

D

K

N

A

146 0

П. И. Алтынов «Геометрия. Тесты. 7-9 кл.»

73 0

?

73 0

C

E

3 4 0

3 4 0

M

B

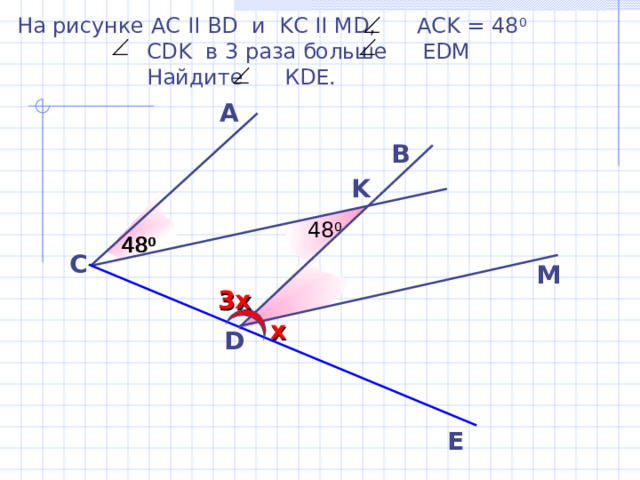
На рисунке АС II BD и KC II MD, ACK = 48 0

CDK в 3 раза больше EDM

Найдите К DE.

A

B

K

48 0

48 0

48 0

C

M

3x

П. И. Алтынов «Геометрия. Тесты. 7-9 кл.»

x

D

E