"Параллельные прямые"

Презентация на тему:

«Признаки параллельных двух прямых. Аксиома параллельных прямых.»

Авторы работы:

Ученицы 9 класса «Г»

Шумикова Полина

Крупина Кристина

Руководитель: учитель математики Иванченко И.А

Параллельные прямые.

Параллельные прямые-от греч. παράλληλος, буквально — идущий рядом.

Две прямые называются параллельными, если лежат в одной плоскости и не пересекаются.

Параллельность прямых a и b обозначается так: a∥b или b∥a.

Параллельные прямые в быту и повседневной жизни.

С параллельными прямыми мы часто встречаемся в окружающей нас жизни, хотя, как правило, редко на этом акцентируем свое внимание. На уроках музыки, открывая нотную тетрадь, сразу же невооруженным взглядом мы видим линии нотного стана. Но параллельные линии мы можем увидеть не только в нотных тетрадях и сборниках песен, но и если внимательно присмотреться к музыкальным инструментам. Ведь струны гитары, арфы или органа также расположены параллельно.

Подняв на улице глаза вверх, вы видите параллельно проходящие электрические провода. Оказавшись в метро или на железной дороге, также не сложно заметить, что рельсы расположены параллельно друг к другу.

Параллельные линии можно встретить повсюду. Они нам постоянно встречаются в быту, живописи. Без них не обойтись и в архитектуре, так как в строительстве зданий строго учитывается понятие параллельности.

Параллельные прямые в быту и повседневной жизни.

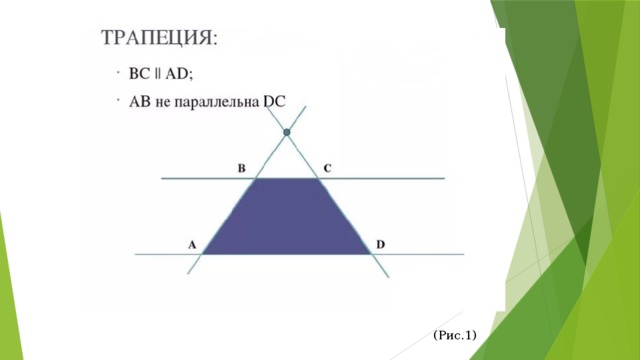
(Рис.1)

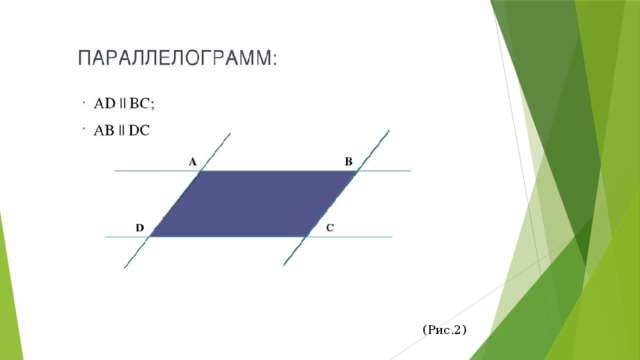
(Рис.2)

Аксиома параллельных прямых.

Аксиома, в свою очередь, такая истина, которую не надо доказывать. В каждой науке есть свои аксиомы, на справедливость которых строят все дальнейшие суждения и их доказательства.

В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.

Иногда эту аксиому называют как одно из свойств параллельных прямых, но на справедливости этой аксиомы строятся многие доказательства в геометрии.

(Рис.3)

(Рис.3)

Аксиома параллельных прямых.

Докажем 1 свойство.

Даны две параллельные прямые a и b. Верно ли, если прямая c параллельна прямой a, то она параллельна и прямой b?

(Рис.4)

(Рис.4)

Аксиома параллельных прямых. Первое свойство .

Используем противоположное суждение.

Допустим, что возможна ситуация, когда прямая c параллельна одной из параллельных прямых - прямой a, пересекает другую прямую b в некоторой точке K.

(Рис.5)

(Рис.5)

Доказательство:

Получается противоречие с аксиомой параллельных прямых. Мы имеем ситуацию, когда через точку проходят две пересекающиеся прямые, которые параллельны одной и той же прямой a. Такого не может быть, значит прямые b и c пересекаться не могут.

Мы доказали, что верно - если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.

(Рис.5)

(Рис.5)

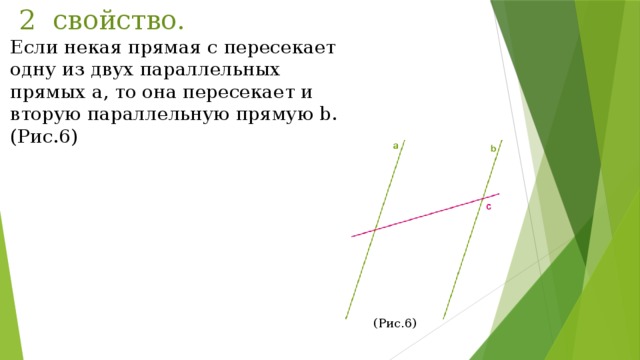
2 свойство.

Если некая прямая c пересекает одну из двух параллельных прямых a, то она пересекает и вторую параллельную прямую b.

(Рис.6)

(Рис.6)

2 свойство.

Таким же методом от противоположного суждения попробуй представить, что возможно ситуация, когда прямая пересекает одну из параллельных прямых, но не пересекает другую.

(Рис.7)

Свойства углов, которые образуются при пересечении двух параллельных прямых с третьей секущей мы уже назвали в первой части теории.

(Рис.7)

При пересечении двух параллельных прямых третьей секущей:

- накрест лежащие углы равны,

- соответственные углы равны,

- сумма односторонних углов равна 180°.

(Рис.8)

(Рис.8)

Признаки параллельности двух прямых

• Теорема.

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, АВ - секущая, 1 и 2 –накрест лежащие, 1 = 2.

Доказать: a∥b.

(Рис.9)

Доказательство:

1 случай:

Предположим, что 1 = 2 = 90 градусов, т.е. эти углы прямые, получим a АВ и b АВ (Рис.4), следовательно a∥b , (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны ).

(Рис.10)

(Рис.10)

2 случай:

Предположим, что 1 и 2 - не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой a. На прямой b от точки В отложим отрезок ВН1 такой, что ВН1 = АН и проведем отрезок ОН1 (Рис. 5).

Получим ОНА = ОН1В по 1 признаку равенства треугольников (по построению ВН1 = АН, АО = ОВ, т.к. О - середина АВ, 1 = 2 по условию), следовательно, 3= 4 и 5 = 6.

Из равенства 3 = 4 следует, что точка Н1 лежит на продолжении луча ОН, т.е. точки О, Н и Н1 лежат на одной прямой, а из равенства 5 = 6 следует, что 6 - прямой, также как и 5 (т.к по построению ОН a ).

Получаем, НН1 a и НН1 b, значит a∥b (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны). Что и требовалось доказать.

(Рис.11)

(Рис.11)

2. Теорема

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Дано: прямые a и b , АВ - секущая, 1 и 2 - соответственные, 1 = 2 (Рис.12).

Доказать:a∥b

Доказательство:

По условию 1 = 2 и 2 = 3, т.к.они вертикальные, откуда 1 = 3, при этом углы 1 и 3 накрест лежащие, следовательно, a∥b (теоремa 1). Что и требовалось доказать.

(Рис.12)

3. Теорема

Если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусов , то прямые параллельны.

Дано: прямые a и b , АВ - секущая, 1 и 2 - односторонние, 1 + 2 = 180 градусов (Рис.13).

Доказать: a∥b.

Доказательство:

Углы 3 и 2 - смежные, значит по свойству смежных углов 3 + 2 = 180 градусов,откуда 3 = 180 градусов - 2, при этом 1 + 2 = 180 градусов, откуда 1 = 180 градусов - 2, тогда 1 = 3, а углы 1 и 3 накрест лежащие, следовательно, a∥b(см. теорему 1). Что и требовалось доказать.

(Рис.13)

Решение задач

Задача 1:

Отрезки AB и CD пересекаются в их общей середине. Докажите, что AC∥BD .

Дано:AO=OB,CO=OD.Докажите, что AC∥BD .

Доказательство:

AO=OB

CO=OD

1 = 2(т.к они вертикальные)

Следовательно, по первому признаку равенства треугольников, СОА= DOB.

Тогда 3= 4.

Поскольку эти углы являются накрест лежащими при прямых AC и BD и секущей АВ, то по первому признаку параллельности прямых ,AC∥BD что и требовалось доказать.

(Рис.14)

(Рис.14)

Задача 2:

Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210°.

Найдите эти углы.

Дано: a∥b,

Найти:

Решение:

Поскольку прямые a и b параллельны, то накрест лежащие углы равны.

Следовательно,

Тогда 2

Ответ:

(Рис.15)

(Рис.15)

Задача 3:

Найдите все углы, образованные при пересечении параллельных прямых a и b с секущей c, если один из углов равен 15°

Дано: a∥b,

Найти: остальные углы

Решение:

1)

2)

3)

Ответ:

(Рис.16)

(Рис.16)

Задача 4:

На рисунке a∥b, прямые m и n – биссектрисы углов 1 и 2. Докажите, что m∥n .

Дано: a∥b, m и n- биссектрисы

Доказать: m∥n

Решение:

Т.к a∥b следовательно

Следовательно,

(Рис.17)

(Рис.17)

Задача 5:

Найдите все углы, образованные при пересечении параллельных прямых a и b с секущей c, если один из углов на 70°.

больше другого.

Дано: a∥b,

Найти: остальные углы. Решение:

+

,

.

2. и (как соответственные)

и ( как вертикальные)

Ответ: ,

(Рис.18)

(Рис.18)

Задача 6:

На рисунке

Дано:

Доказать:a∥b

Доказательствo:

1)

2)

3)

Тогда, поскольку сумма внутренних углов равна , то по третьему признаку параллельности прямых, , что и требовалось доказать.

(Рис.19)

(Рис.19)

Задача 7:

Дано:ABC=BAD

Доказать:AB∥BD, AD∥BC

Доказательство:

На рисунке видно, что АВ – общая сторона.

Из равенства треугольников следует, что AD=CB, AC=BD.

Тогда

Тогда по первому признаку параллельности прямых AC∥BD.

Тогда по первому признаку параллельности прямых AD∥BC. (Рис.20)

(Рис.20)

Задача 8:

°

Дано: АС∥BD; AC = AB;

Найти:

Решение:

Т.к. АС∥BD, то ABD = 40° ( как соответственные)

Т.к. АВС р\б, то АВС = АСВ ( по свойству р\б треугольника)

Т.к. АС BD, то АСВ = CBD ( как накрест лежащие)

Следовательно: ВС – биссектриса

(Рис.21)

(Рис.21)

Задача 9:

Дано:

Доказать: АВ∥CD

Доказательство:

1) Т.к. АВС р\б, то

2)

3) Т.к. CD – биссектриса, то

4)

Т.к. эти углы равны, то АВ∥CD

Что и требовалось доказать.

(Рис.22)

(Рис.22)

Задача 10:

Дано: a∥b, CD – секущая

Доказать:

Доказательство:

Проведём через точку С прямую а1 так, чтобы внутренние накрест лежащие углы, образованные секущей СD и прямыми a и b, были равны.

По признаку параллельности прямых прямые a1 и b параллельны, а т.к. через точку С может проходить только одна прямая, параллельная прямой b, то прямая а совпадает с прямой а1.

Значит внутренние накрест лежащие углы, образованные параллельными прямыми a и b с секущей С, равны, т.е.

Учитывая, что

(Рис.23)

Список используемой литературы:

https://interneturok.ru/lesson/geometry/7-klass/parallelnye-pryamye/zadachi-na-priznaki-parallelnosti-dvuh-pryamyh

http://ru.convdocs.org/docs/index-62584.html

https://www.yaklass.ru/p/geometria/10-klass/parallelnost-priamykh-i-ploskostei-10435/parallelnost-priamykh-priamoi-i-ploskosti-9253/re-15895537-90b0-4f1f-b6bd-4ed1e3c5b600

http://www.cleverstudents.ru/line_and_plane/parallel_lines.html

http://wiki.eduvdom.com/subjects/geometry/%D0%BF%D1%80%D0%B8%D0%B7%D0%BD%D0%B0%D0%BA%D0%B8_%D0%BF%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D0%B8_%D0%B4%D0%B2%D1%83%D1%85_%D0%BF%D1%80%D1%8F%D0%BC%D1%8B%D1%85

http://edufuture.biz/index.php?title=%D0%9F%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BF%D1%80%D1%8F%D0%BC%D1%8B%D0%B5._%D0%9F%D0%BE%D0%BB%D0%BD%D1%8B%D0%B5_%D1%83%D1%80%D0%BE%D0%BA%D0%B8

http://5klass.net/geometrija-7-klass/Parallelnost-dvukh-prjamykh/013-Primery-parallelnostej-v-realnoj-zhizni.html

https://www.yaklass.ru/materiali?mode=lesson&lsnid=177

https://videouroki.net/razrabotki/material-po-matematike-aksioma-parallelnykh-pryamykh.html

https://budu5.com/manual/chapter/3387

https://ru.wikipedia.org/wiki/%D0%9F%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BF%D1%80%D1%8F%D0%BC%D1%8B%D0%B5

https://www.kursoteka.ru/course/2748/lesson/8913/unit/22789

http://ru.solverbook.com/