
Параллелограмм. Признаки параллелограмма. 8 класс
Составитель: Бычкова Т.В., учитель МБОУ СОШ №3 с.Хороль Приморский край

Цели урока
- Ввести понятие параллелограмма и рассмотреть его свойства
- Научиться применять теоретические знания при решении задач
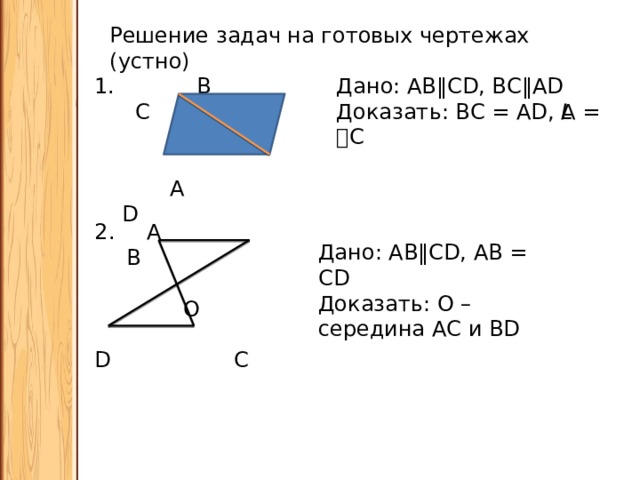
Решение задач на готовых чертежах (устно)
Дано: АВ ‖CD, ВС‖AD
1. В С
Доказать: ВС = AD, 𝘓А = 𝘓С
А D
О
D C
Дано: АВ ‖CD, АВ = CD
Доказать: О – середина АС и BD
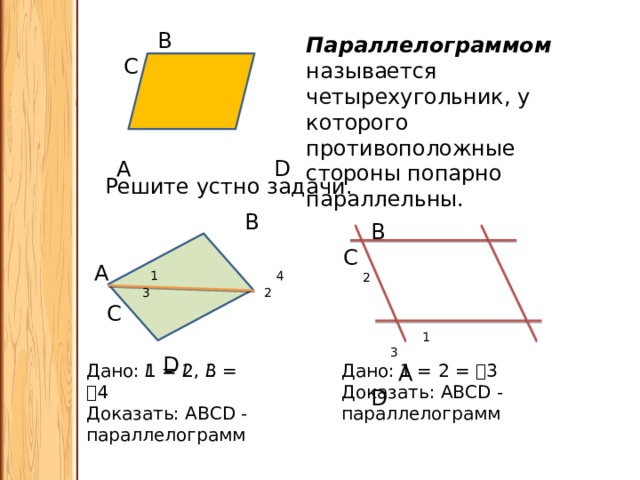
B C
A D
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Решите устно задачи.
В
А 1 4
3 2 С
D
В С
2
1 3
А D
Дано: 𝘓1 = 𝘓2, 𝘓3 = 𝘓4
Дано: 𝘓1 = 𝘓2 = 𝘓3
Доказать: ABCD - параллелограмм
Доказать: ABCD - параллелограмм
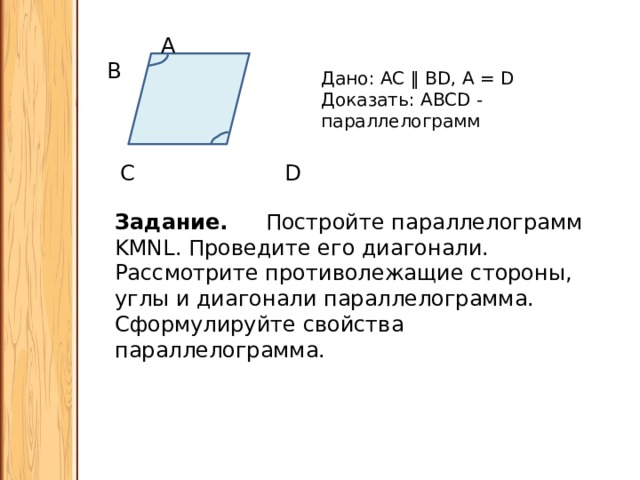
A B
C D
Дано: АС ‖ BD, 𝘓А = 𝘓D
Доказать: ABCD - параллелограмм
Задание. Постройте параллелограмм KMNL. Проведите его диагонали. Рассмотрите противолежащие стороны, углы и диагонали параллелограмма. Сформулируйте свойства параллелограмма.
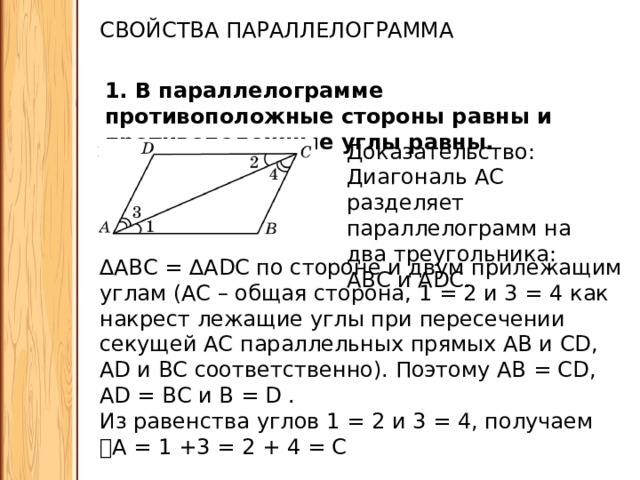
СВОЙСТВА ПАРАЛЛЕЛОГРАММА
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
Доказательство:
Диагональ АС разделяет параллелограмм на два треугольника: АВС и ADC.
∆ АВС = ∆ADC по стороне и двум прилежащим углам (АС – общая сторона, 𝘓1 = 𝘓2 и 𝘓3 = 𝘓4 как накрест лежащие углы при пересечении секущей АС параллельных прямых АВ и CD, AD и ВС соответственно). Поэтому АВ = CD, AD = ВС и 𝘓В = 𝘓D .
Из равенства углов 𝘓1 = 𝘓2 и 𝘓3 = 𝘓4, получаем
𝘓 А = 𝘓1 +𝘓3 = 𝘓2 + 𝘓4 = 𝘓С
ч.т.д.
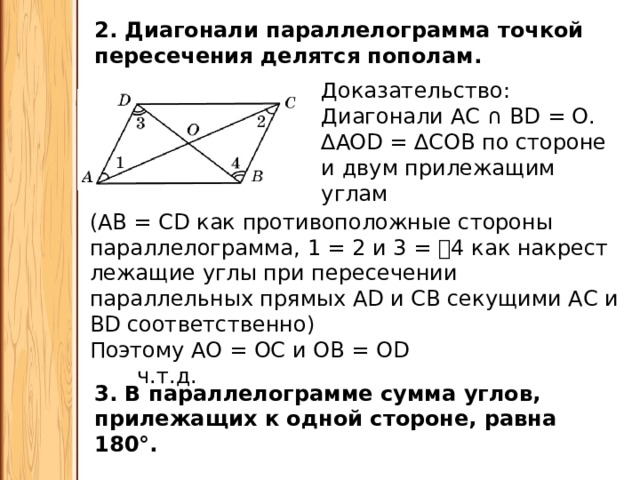
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Доказательство:
Диагонали АС ∩ BD = О.
∆ AOD = ∆COB по стороне и двум прилежащим углам
(АВ = CD как противоположные стороны параллелограмма, 𝘓1 = 𝘓2 и 𝘓3 = 𝘓4 как накрест лежащие углы при пересечении параллельных прямых AD и СВ секущими АС и BD соответственно)
Поэтому АО = ОС и ОВ = OD ч.т.д.
3. В параллелограмме сумма углов, прилежащих к одной стороне, равна 180 °.

РЕШЕНИЕ ЗАДАЧ
- № 8, 9 – рабочая тетрадь по геометрии 8 класс
- № 372 (а,б), 375, 376(б,д)

Домашнее задание

Литература и ресурсы
- Учебник «Геометрия 7-9» Л.С. Атанасян
- Поурочные разработки по геометрии 8 класс, Н.Ф. Гаврилова
- Интернет-ресурсы


































