Параллельность прямых

Параллельность прямых

Об аксиомах геометрии

• Некоторые утверждения о свойствах геометрических фигур принимаются в качестве исходных положений, на основе которых доказываются далее теоремы и, вообще, строится вся геометрия. Такие исходные положения называются АКСИОМАМИ .

Об аксиомах геометрии

• Все эти аксиомы являются наглядно очевидными и не вызывают сомнений.
• Само слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».

Об аксиомах геометрии

• Такой подход к построению геометрии, когда сначала формулируются исходные положения — аксиомы, а затем на их основе путем логических рассуждений доказываются другие утверждения, зародился еще в глубокой древности и был изложен в знаменитом сочинении «Начала» древне­греческого ученого Евклида (примерно 365—300 гг. до н. э.).

Об аксиомах геометрии

• Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в курсах геометрии, а сама геометрия, изложенная в «Началах», называется евклидовой геометрией.

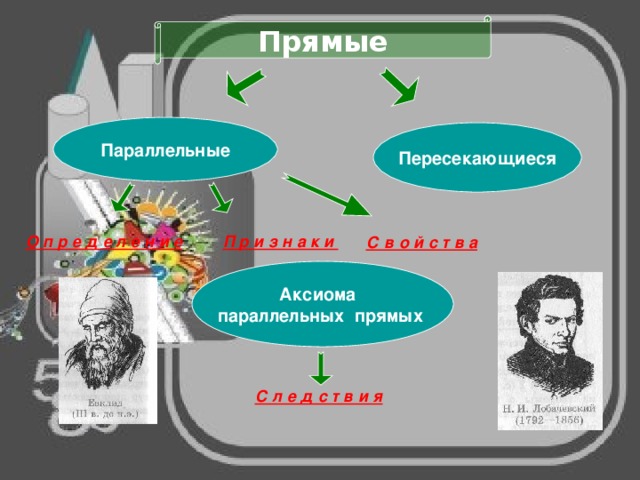
Прямые

Параллельные

Пересекающиеся

Аксиома

параллельных прямых

« Параллельные суть прямые,

которые, находясь в одной плоскости и

будучи продолжены в обе

стороны неограниченно,

ни с той, ни с другой

стороны между

собой не встречаются.»

[2]

«Две прямые, лежащие

в одной плоскости

и равностоящие

друг от друга.» [1]

Параллельные прямые -это прямые, лежащие в одной плоскости и не пересекающиеся.

b

a

a=b

b

a

[1]

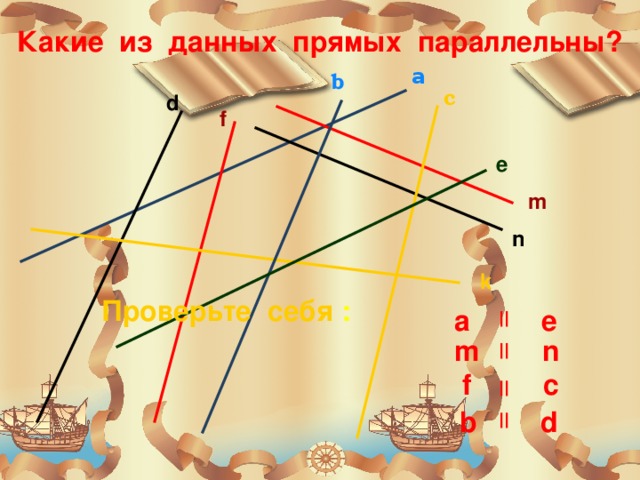
Какие из данных прямых параллельны?

a

b

с

d

f

e

m

n

k

Проверьте себя :

a e

m n

f c

b d

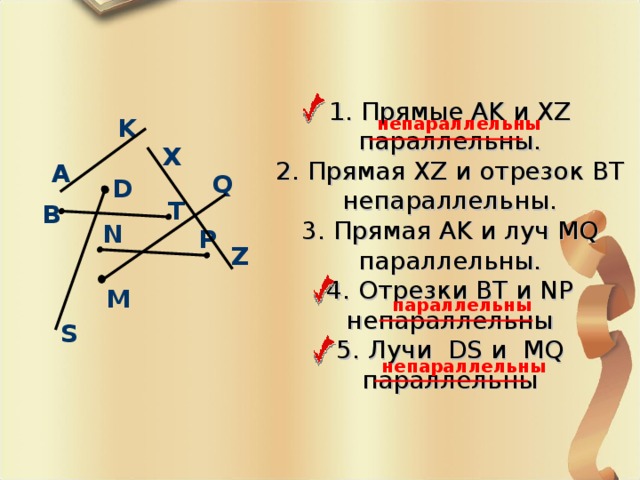
1. Прямые AK и XZ параллельны. 2. Прямая XZ и отрезок BT непараллельны. 3. Прямая AK и луч MQ параллельны. 4. Отрезки ВТ и NP непараллельны 5. Лучи DS и MQ параллельны

K

непараллельны

X

A

Q

D

T

B

N

P

Z

M

параллельны

S

непараллельны

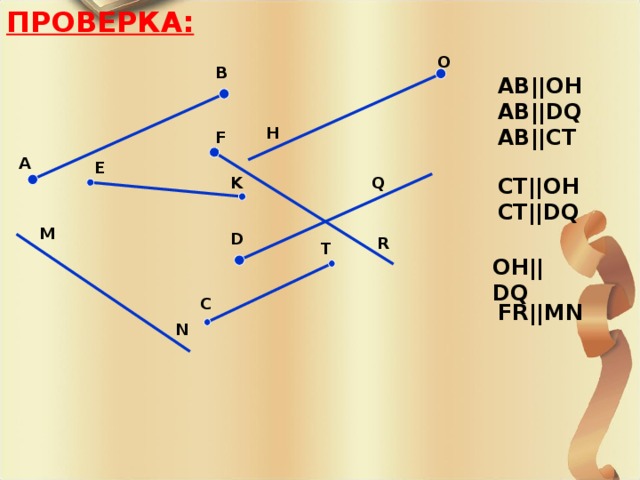
ПРОВЕРКА:

O

B

AB||OH

AB||DQ

AB||CT

H

F

A

E

Q

K

CT||OH

CT||DQ

M

D

R

T

OH||DQ

C

FR||MN

N

Пятый постулат Евклида.

Через точку не лежащую на прямой, можно провести только одну прямую параллельной данной.

«Начала»

И стояла геометрия Евклида,

Как египетская чудо-пирамида.

Строже выдумать строение невозможно,

Лишь одна была в ней глыба ненадёжна.

Аксиома называлась «параллели».

Разгадать её загадку не сумели.

Аксиома параллельных прямых

• Оказывается этот вопрос имеет большую историю. В «Началах» Евклида содержится постулат (пятый постулат Евклида), из которого следует, что через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной . Многие математики, начиная с древних времен, предпринимали попытки доказать пятый постулат Евклида, т. е. вывести его из других аксиом. Однако эти попытки каждый раз оказывались неудачными.

Аксиома параллельных прямых

• И лишь в прошлом веке было окончательно выяснено, что утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой. Огромную роль в решении этого вопроса сыграл великий русский математик Николай Иванович Лобачевский (1792—1856).

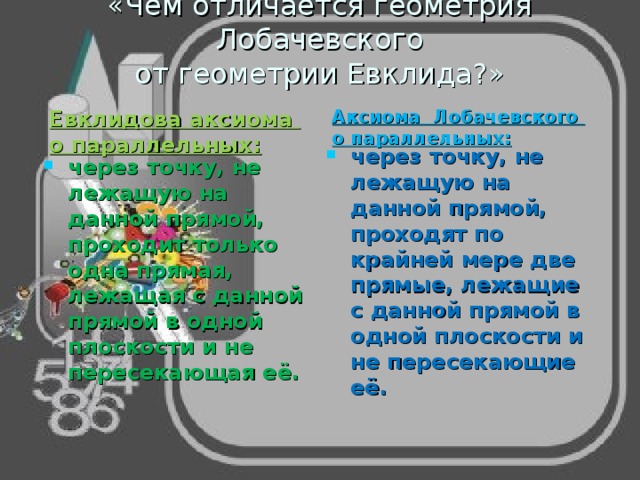
«Чем отличается геометрия Лобачевского от геометрии Евклида?»

Евклидова аксиома о параллельных:

Аксиома Лобачевского о параллельных:

• через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

• через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её.

Очень часто встречается параллельность прямых в природе.

При строительстве зданий

строго учитывается

понятие параллельности

Самый наглядный пример параллельности прямых - железнодорожное полотно

Гипотеза

Нас повсюду окружают параллельные прямые и мы не можем жить без них.

Московский театр (архитектор Бове)

Триумфальная арка в Париже

замыкание,

крушение поезда

нет электричества

bIIc

b

c

c

b

b II c

А

b

c

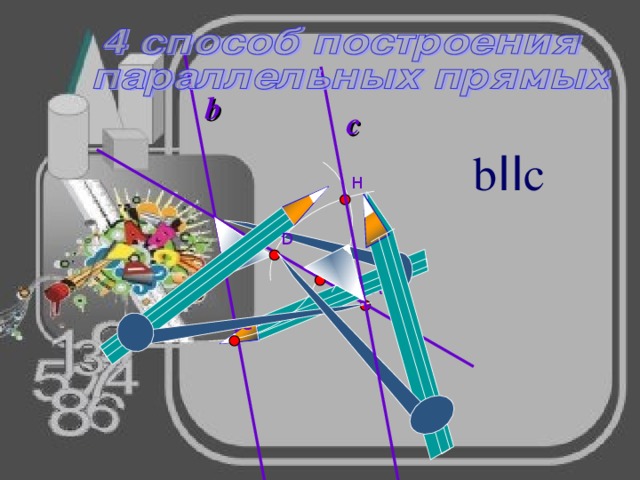
b

c

b II c

H

D

B

А

C

Иллюзия Геринга (иллюзия веера)

Прямые, на самом деле, параллельны.

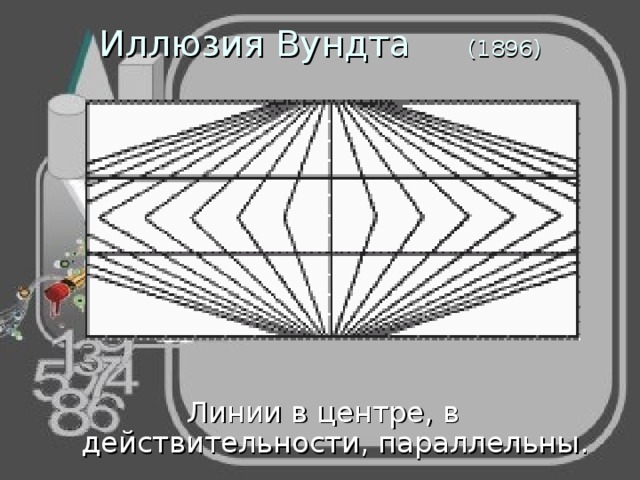
Иллюзия Вундта (1896)

Линии в центре, в действительности, параллельны.

Здесь тоже линии параллельны

32

Иллюзия кафе "Wall"

Параллельны ли горизонтальные линии?

Да, параллельны!

Иллюзия обнаружена Р. Грегори в кафе "Wall"

в Бристоле (Richard Gregory, 1979).

Красные наклонные линии - прямые , хотя и кажутся изогнутыми.

Иллюзия Цолльнера (Zolliner, 1860).

Параллельные прямые кажутся изогнутыми.

Иллюзия Поггендорфа (Poggendorf, 1860)

Какие линии лежат на одной прямой: АС или ВС?

На одной прямой лежит линия BC, а не AC, как кажется.

Иллюзия с витыми веревками (James Frazer, 1908).

Это прямые или нет?

Это параллельные прямые.

Иллюзия У. Эренштейна (W. Ehrenstein, 1921)

Квадрат кажется искаженным.

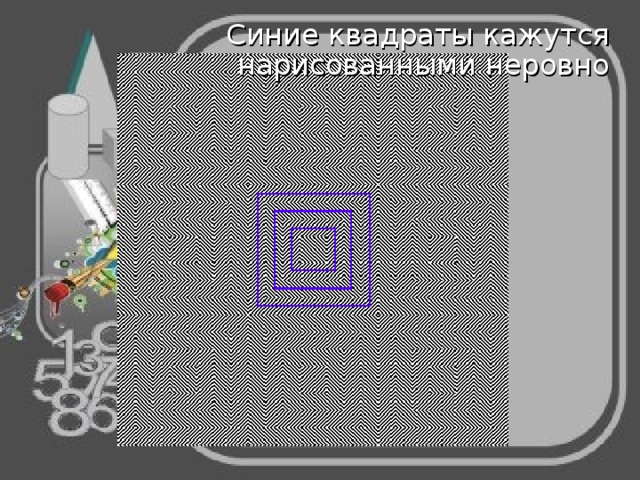
Синие квадраты кажутся нарисованными неровно

Узор как бы изгибается во внутрь?

Все квадраты не самом деле

не искажены .

Узор как бы выступает вперед?

На рисунке все квадраты

не искажены .

Следствия из аксиомы

Утверждения, которые выводятся непосредственно из аксиом или теорем, называются следствиями.

Следствия из аксиомы

Следствие 1°. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

• Дано: ,
• Доказать:
• Доказательство: Если c не пересекается c b , то
• Значит через точку М проходит две прямые а и с параллельные b , это противоречит аксиоме, значит

с

а

М

b

Следствия из аксиомы

Следствие 2°. Если две прямые параллельны третьей прямой, то они параллельны.

• Дано: a||c, b||c
• Доказать: a||b
• Доказательство: Пусть a не параллельна b , т.е
• Тогда через точку М проходит две прямые а и b параллельные c , это противоречит аксиоме, значит a||b .

а

М

b

с

Решение задач

Через точку, не лежащую на данной прямой p , проведены четыре прямые. Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи.

А

р

Ответ: три или четыре

Математический диктант

«Аксиома параллельных прямых»

№ 1.

Две прямые на плоскости, которые не пересекаются, называются…

№ 2

• Утверждения о свойствах геометрических фигур, принимаемые в качестве исходных положений, на основе которых доказываются теоремы, называются…

№ 3

• Через точку, не лежащую на прямой, можно провести прямую, … данной, и притом только …

№ 4

• Утверждения, которые выводятся непосредственно из аксиом или теорем называются…

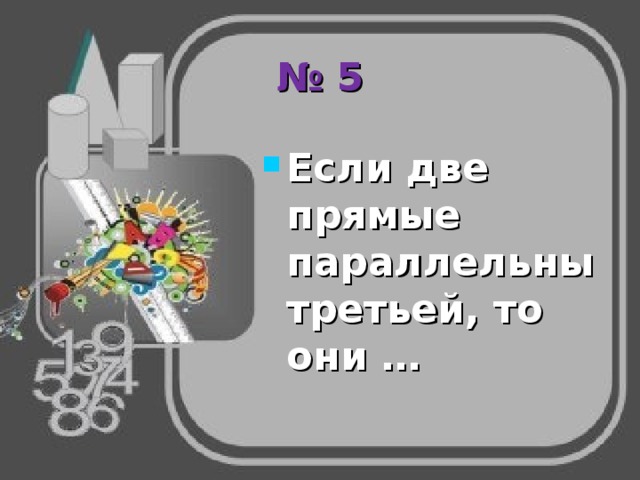
№ 5

• Если две прямые параллельны третьей, то они …

№ 6

• Если прямая пересекает одну из двух параллельных прямых, то она …

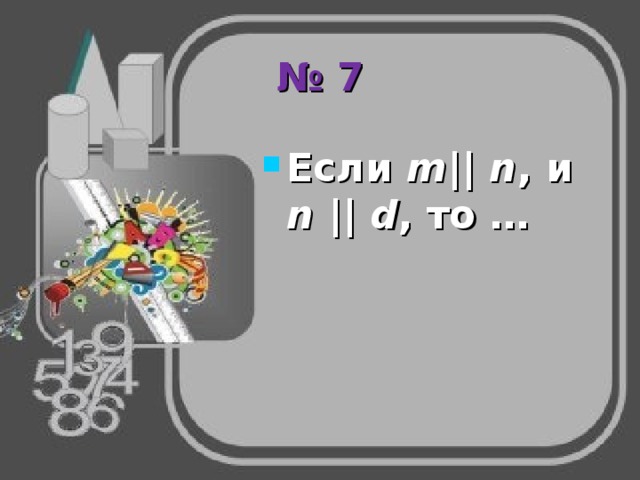
№ 7

• Если m || n , и n || d , то …

ПРОВЕРЬ СЕБЯ

• Параллельными
• Аксиомы
• Параллельную, одну
• Следствия
• Параллельны
• Пересекает и другую
• m || d

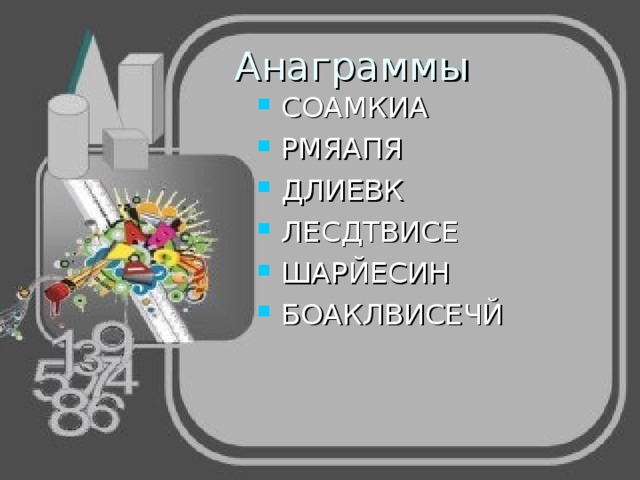
Анаграммы

• СОАМКИА
• РМЯАПЯ
• ДЛИЕВК
• ЛЕСДТВИСЕ
• ШАРЙЕСИН
• БОАКЛВИСЕЧЙ

Домашняя работа