Параллельные прямые

Геометрия глава 3 «Параллельные прямые».

Подготовила Иванова Настя ученица 9 класса СПб лицей 488 ( учитель Курышова Н.Е. )

Оглавление:

Параллельные прямые

Обозначение параллельных прямых

Параллельные отрезки

Признаки параллельности двух прямых

Теорема о параллельности 2 прямых с использованием накрест лежащих углов.

Теорема о параллельности 2 прямых с использованием соответственных углов.

Практические способы построения параллельных прямых.

Евклид. Сочинение «Начала»

Аксиома

Аксиома параллельных прямых

Следствие

Следствие 1 0

Следствие 2 0

Н. И. Лобачевский

Пятый постулат

Теоремы об углах, образованных двумя параллельными прямыми и секущей.

Теорема о равности накрест лежащих углов.

Следствие

Теорема о равности накрест соответственных углов.

Теорема о сумме односторонних углов.

конец

Параллельные прямые-

это прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются.

A A 1

A , B

A 1 ,B 1

B B 1

Параллельность прямых a и b обозначают так: a||b

a

b

они параллельны. ч.т.д. c a b " width="640"

Дано: прямые a и b , пересечённые c Доказать: прямые a и b параллельны. Доказательство: Прямые a и b перпендикулярны с ( a и b не пересекаются) = они параллельны. ч.т.д.

c

a

b

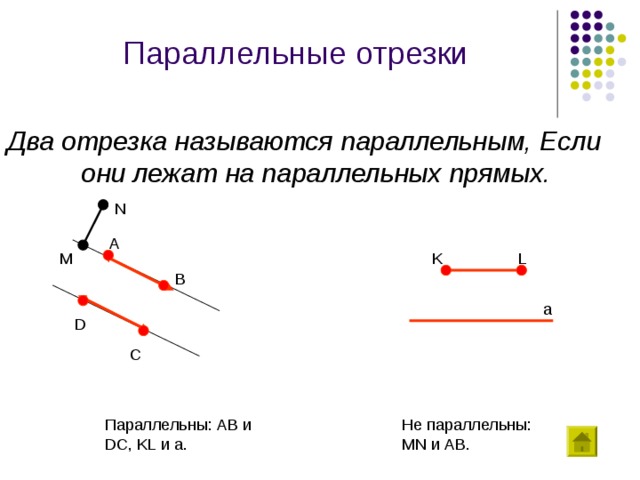
Параллельные отрезки

Два отрезка называются параллельным, Если они лежат на параллельных прямых.

N

A

M

L

K

B

a

D

C

Не параллельны: MN и AB .

Параллельны: AB и DC , KL и a .

Признаки параллельности двух прямых

Прямая с называется секущей по отношению к прямым a и b , если она пересекает их в двух точках. При пересечении прямых a и b секущей c образуется 8 углов. Некоторые пары углов имеют специальные названия:

Накрест лежащие: 3 и 5; 4 и 6.

Односторонние: 4 и 5; 3 и 6.

Соответственные: 1 и 5; 4 и 8;

2 и 6; 3 и 7.

c

b

b

1 2

4 3

5 6

a

8 7

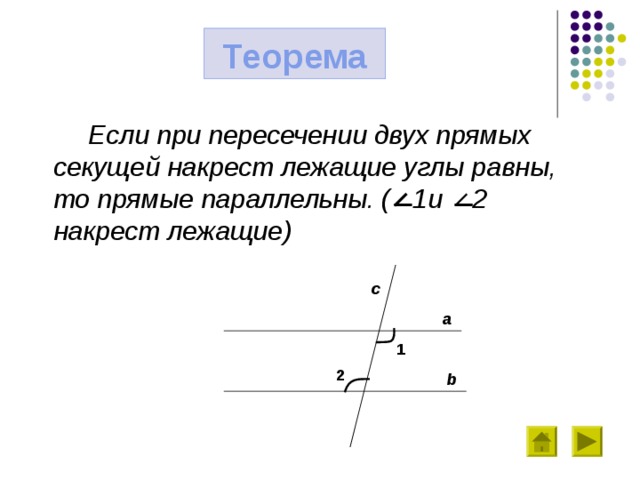
Теорема

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. ( 1 и 2 накрест лежащие)

c

a

1

2

b

Доказательство.

Дано: прямые a и b ; секущая AB ; 1= 2 (накрест лежащие)

Доказать: a||b .

Доказательство:

а)Если 1 и 2 прямые, то a и b перпендикулярны прямой AB и параллельны.

c

a

1

2

b

O Н A = ОН 1 В по двум сторонам и углу между ними = 3= 4 и 5 = 6 О, Н и Н 1 лежат на одной прямой 6 – прямой а НН 1 и b НН 1 Они параллельны. a H A 5 1 3 О 4 2 6 b ч.т.д. B H 1 " width="640"

Рассмотрим случай, когда углы 1 и 2 не прямые:

б)Из середины О отрезка АВ проведём перпендикуляр ОН к прямой а.

ВН 1 = АН = O Н A = ОН 1 В по двум сторонам и углу между ними =

• 3= 4 и 5 = 6
• О, Н и Н 1 лежат на одной прямой
• 6 – прямой
• а НН 1 и b НН 1
• Они параллельны.

a

H A

5 1 3

О

4 2 6

b

ч.т.д.

B H 1

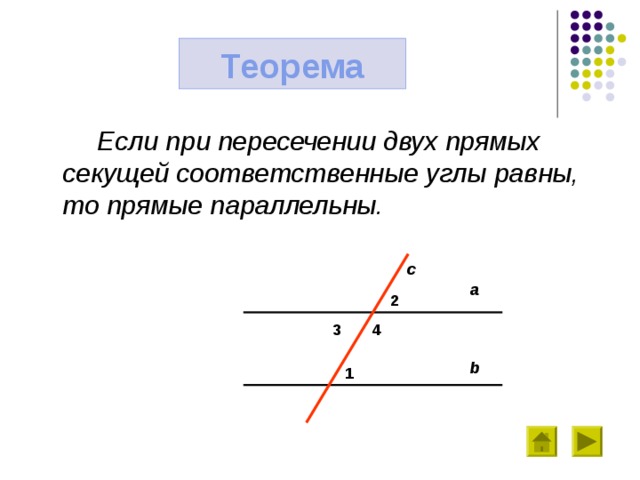
Теорема

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

c

a

2

3 4

b

1

Доказательство.

Дано: прямые а и b ; секущая с; 1= 2(секущие)

Доказать: a || b

Доказательство: Т.к. 2 и 3 –вертикальные,

то 2 = 3

• 1= 3
• Но 1 и 3 – накрест лежащие
• a || b

c

a

2

3 4

ч.т.д.

b

1

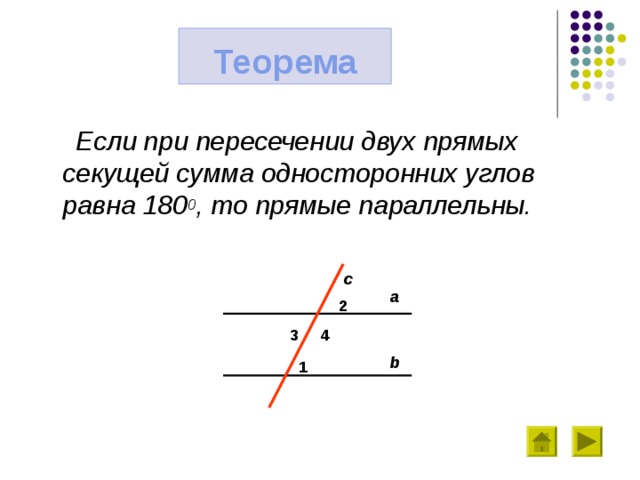
Теорема

Если при пересечении двух прямых секущей сумма односторонних углов равна 180 0 , то прямые параллельны.

c

a

2

3 4

b

1

= 3 + 4=180 0 1 = 3 (накрест лежащие) a || b c a 2 3 4 ч.т.д. b 1 " width="640"

Доказательство.

Дано: Пусть при пересечении прямых a и b секущей с 1 + 4= 180 0

Доказать: a || b

Доказательство:

Т.к. 3 и 4 – смежные =

= 3 + 4=180 0

• 1 = 3 (накрест лежащие)
• a || b

c

a

2

3 4

ч.т.д.

b

1

Практические способы построения параллельных прямых.

c

b

• С помощью чертёжного угольника и линейки
• С помощью рейсшины
• С помощью малка

задачи

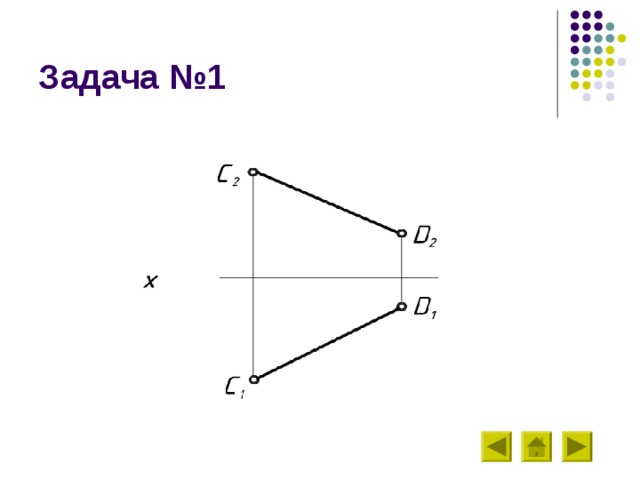
Задача №1

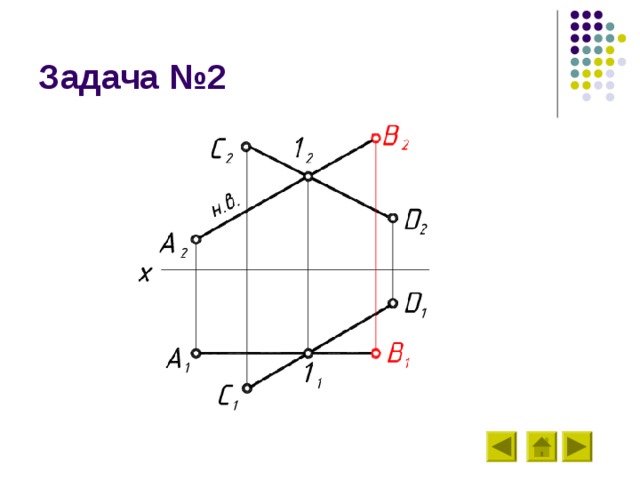
Задача №2

Евклид

(365-300 гг. до н.э.)

Сочинение «Начала»

Аксиома-

Положение принимаемое без доказательств и лежащие в основе доказательств истинности других положений

Аксиома параллельных прямых

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная.

C

a

b

Следствие -

Утверждение, которое выводится непосредственно из аксиом или теорем .

Следствие 1 0

Если прямая пересекает одну из двух параллельных прямых. То она пересекает и другую.

Доказательство:

Дано: а || b ; точка М пересекает a .

Доказать: с пересекает b .

Доказательство:

Если бы прямая с не пересекала b , то через M проходили а и с, параллельные b

НО это противоречит аксиоме параллельных прямых

• c пересекает b.

ч.т.д.

c

c

M

M

a

a

b

b

Следствие 2 0

Если две прямые параллельны третьей прямой, то они параллельны.

a

b

c

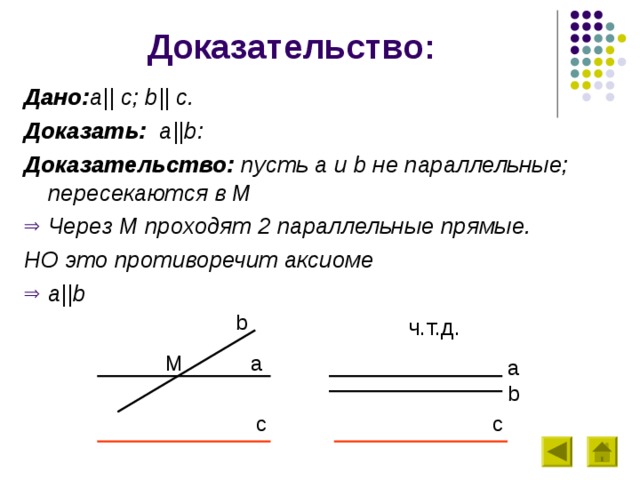
Доказательство:

Дано: a|| c ; b|| c.

Доказать: a||b :

Доказательство: пусть a и b не параллельные; пересекаются в М

• Через М проходят 2 параллельные прямые.

НО это противоречит аксиоме

• a||b

ч.т.д.

b

a

M

a

b

c

c

Н. И. Лобачевский

(1792-1856гг.)

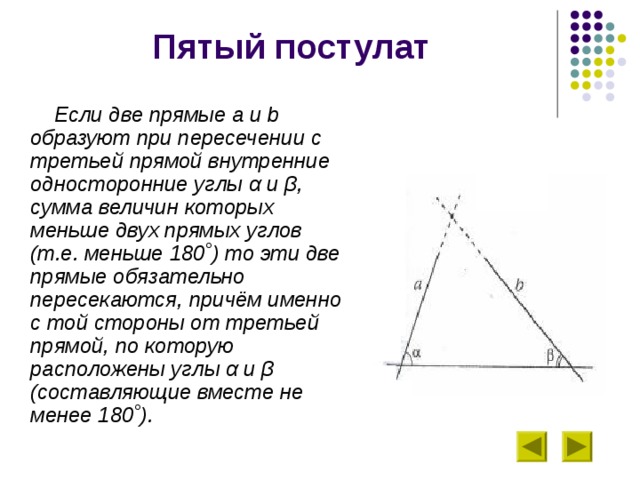
Если две прямые a и b образуют при пересечении с третьей прямой внутренние односторонние углы α и β, сумма величин которых меньше двух прямых углов (т.е. меньше 180˚) то эти две прямые обязательно пересекаются, причём именно с той стороны от третьей прямой, по которую расположены углы α и β (составляющие вместе не менее 180˚).

Сложность формулировки пятого постулата и его неубедительность привели к тому, что очень многие математики, жившие после Евклида, старались исключить этот постулат из списка аксиом, т.е. доказать его как теорему с помощью остальных аксиом Евклида. В «сражениях» с пятым постулатом особенно далеко продвинулись Ламберт, Саккери и Лежандр.

В начале XIX в. русский математик профессор Николай Иванович Лобачевский делал попытки, но первое время он шёл тем же путём что и его предшественники, т.е. пытался рассуждать от противного. Допустив, что пятый постулат неверен, а остальные аксиомы справедливы, мы рано или поздно придем к противоречию. Этим противоречием он и будет доказан.

Тогда Лобачевский предпринимает попытку использовать могущество формул. Применяя выведенную им функцию П(х), он получает зависимости, позволяющие по сторонам треугольника вычислять его углы. И оказывается что в любом треугольнике сумма углов меньше 180˚. Значит в четырёхугольнике Саккери сумма углов меньше 360˚. Это означает, что мы находимся в условиях гипотезы острого угла – когда в четырёхугольнике Саккери четвёртый угол φ

Теоремы об углах, образованных двумя параллельными прямыми и секущей.

Во всякой теореме различают две части: условие и заключение.

Условие – это то, что дано.

Заключение – то, что требуется доказать.

Обратная теорема – теорема, в которой условием являются заключение данной теоремы, а заключением - условие данной теоремы.

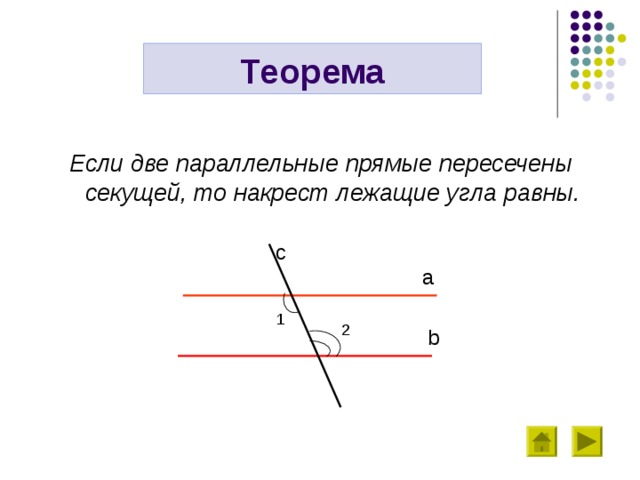
Если две параллельные прямые пересечены секущей, то накрест лежащие угла равны.

a

1

2

b

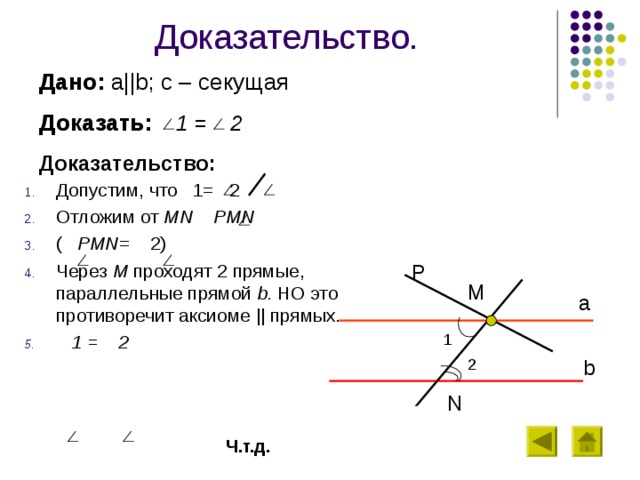
Доказательство.

Дано: a||b ; c – секущая

Доказать: 1 = 2

Доказательство:

• Допустим, что 1= 2
• Отложим от MN PMN
• ( PMN = 2)
• Через M проходят 2 прямые, параллельные прямой b . НО это противоречит аксиоме || прямых.
• 1 = 2

P

M

a

1

2

b

N

Ч.т.д.

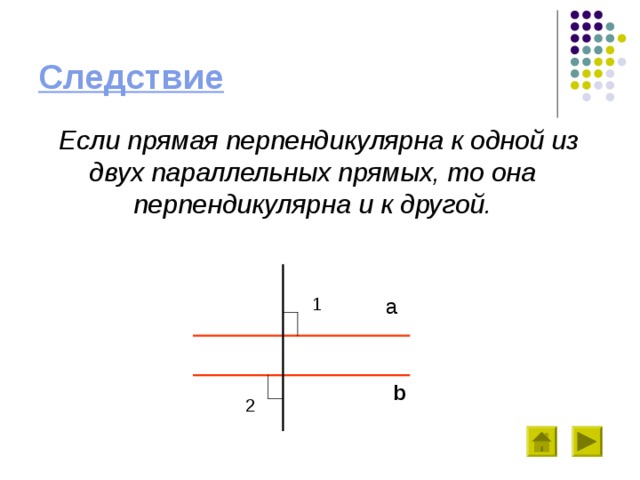
Следствие

Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

a

1

b

2

пересекает и b 1= 2 Т.к. 1=90 о и 2=90 о , т.е. с b ч.т.д. 1 a b 2 " width="640"

Дано: a || b , с a ( 1= 90 о )

Доказать: с b

Доказательство:

Т.к. с пересекает a = пересекает и b

1= 2

Т.к. 1=90 о и 2=90 о , т.е. с b

ч.т.д.

1

a

b

2

Теорема

Если две параллельные прямые пересечены секущей, то соответственные углы равны.

c

b

2

3 4

a

1

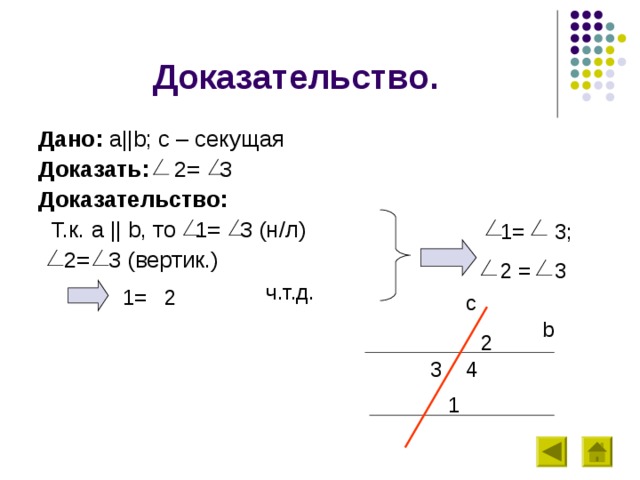
Дано: a||b ; c – секущая

Доказать: 2= 3

Доказательство:

Т.к. a || b , то 1= 3 (н/л)

2= 3 (вертик.)

c

b

2

3 4

1

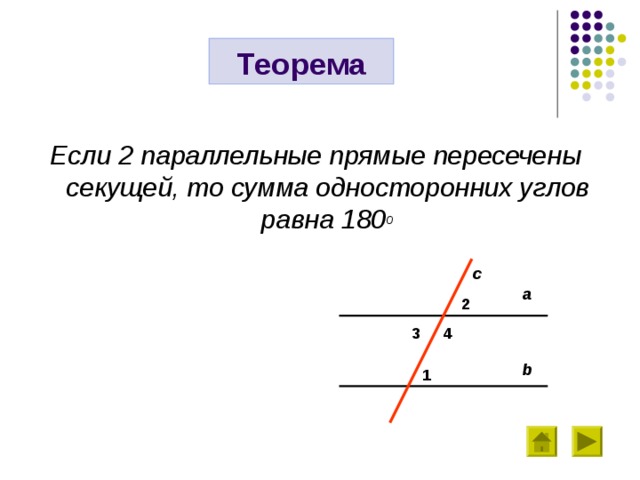
Теорема

Если 2 параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 о

c

a

2

3 4

b

1

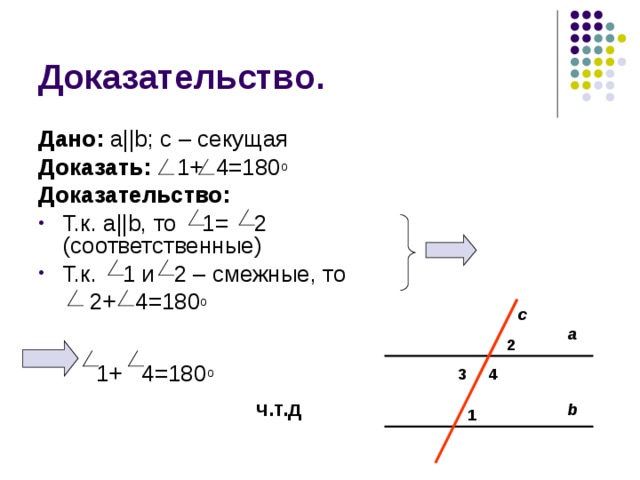
Дано: a||b ; c – секущая

Доказать: 1+ 4=180 о

Доказательство:

• Т.к. a||b , то 1= 2 (соответственные)
• Т.к. 1 и 2 – смежные, то

2+ 4=180 о

1+ 4=180 о

c

a

2

3 4

ч.т.д

b

1

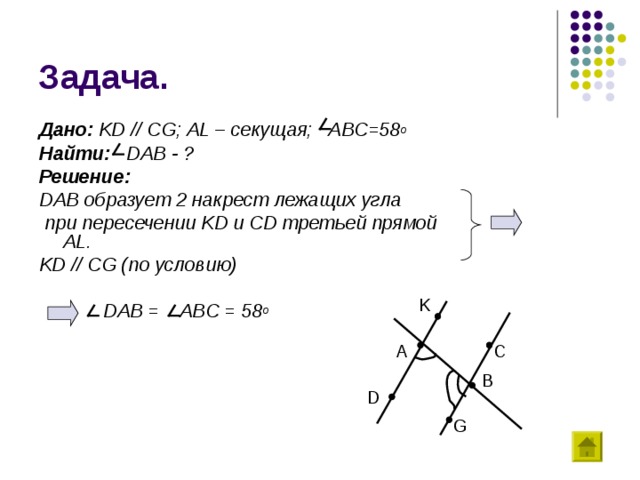
Дано: KD // CG ; AL – секущая; ABC=58 о

Найти: DAB - ?

Решение:

DAB образует 2 накрест лежащих угла

при пересечении KD и CD третьей прямой AL .

KD // CG (по условию)

DAB = ABC = 58 о

K

A

C

B

D

G

Конец