
Муниципальное бюджетное общеобразовательное учреждение
города Абакана «Средняя общеобразовательная школа № 26 с углубленным изучением отдельных предметов»
Секция математики
Паркеты
Авторы:
Галимов Роман Александрович,
ученик 5Д класса
Макаров Кирилл Максимович
ученик 5Д класса
Руководитель:
Власова Лариса Валентиновна,
учитель математики
Абакан, 2022
Оглавление
Введение 3
1 Теоретическая часть 4
1.1 Понятие паркета 4
1.2 Как знания о паркетах помогают делать открытия в физике и химии 7
1.3 Простейшие фигуры и движения для построения паркетов 8
1.4 Примеры построения паркетов 12
Практическая часть 14
Заключение 15
Список использованных источников 16
Введение
Геометрия – один из интереснейших разделов математики. Она знакомит школьников с разнообразием форм окружающего мира, способствует развитию пространственного воображения и логического мышления, приобретению необходимых навыков в изображении, моделировании и конструировании фигур, измерении геометрических величин. Геометрия имеет яркую многовековую историю, она связана с именами знаменитых ученых: Пифагора, Евклида, Архимеда, Лобачевского и многих других.
Геометрия очень емкая наука, включающая в себя множество разделов и тем. В представленной работе затрагивается лишь одна из них – «Паркеты». Тема интересна тем, что доступна для понимания даже тем, кто не приступил к изучению геометрии в школе, требует представления о небольшом количестве плоских многоугольников и видах движения, дает возможность наблюдать результаты работы во многих областях жизнедеятельности: в быту, строительстве, архитектуре, работах художников и дизайнеров, трудах физиков, химиков и т.д.
Актуальность выбранной темы заключается в возможности украшать площади и улицы, жилища и предметы быта с помощь составления разнообразных красочных бордюров, орнаментов и паркетов, а также, в изучении свойств кристаллов, создании новых материалов.
Целью учебного исследования является формирование представления о паркете, видах и способах его составления.
Для достижения поставленной цели сформулированы следующие задачи:
изучить и выбрать для написания работы информационные источники по теме «Паркеты»;
сформировать представление о паркете, его видах и способах построения;
изучить несложные плоские геометрические фигуры (правильный многоугольник, четырехугольник и его виды, некоторые виды преобразований плоскости);
научиться с помощью графической системы GeoGebra строить паркеты.
Объектом исследования являются паркеты, предметом – способы построения паркетов из несложных фигур с помощью графических средств.
Проблема исследования заключается в практическом применении графических средств для составления паркетов.
Гипотеза состоит в том, что с помощью треугольников, разных видов четырехугольников и некоторых правильных многоугольников возможно составление паркетов.
При написании работы были применены такие теоретические и практические методы исследования, как наблюдение, изучение, анализ и эксперимент.
Работа состоит из введения, теоретической и практической частей, заключения и списка использованных источников. Работа написана в текстовом редакторе Word на 22 страницах, содержит 29 рисунков, 13 информационных источников.
1 Теоретическая часть
1.1 Понятие паркета
С паркетами люди встречаются в повседневной жизни: на улицах, в оформлении зданий, в разных учреждениях, квартирах, в работах художников и т.д. В теме «паркеты» отражены основные понятия геометрии: разные виды многоугольников, разные виды движения.
Паркетом на плоскости называется такое заполнение плоскости многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек [1, с. 149].
Паркет называется правильным, если он состоит из правильных многоугольников, и вокруг каждой вершины правильные многоугольники расположены одним и тем же способом. Ниже на рисунке 1 приведены примеры правильных паркетов. На рисунке 2 приведены примеры правильных паркетов, составленных из правильных многоугольников с разным числом сторон.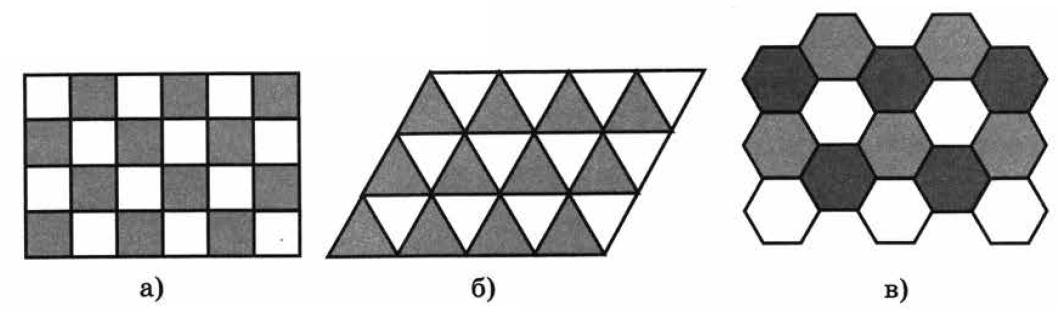
Рисунок 1 – Примеры правильных паркетов (заполнение плоскости а – квадратами; б – правильными треугольниками; в – правильными шестиугольниками)
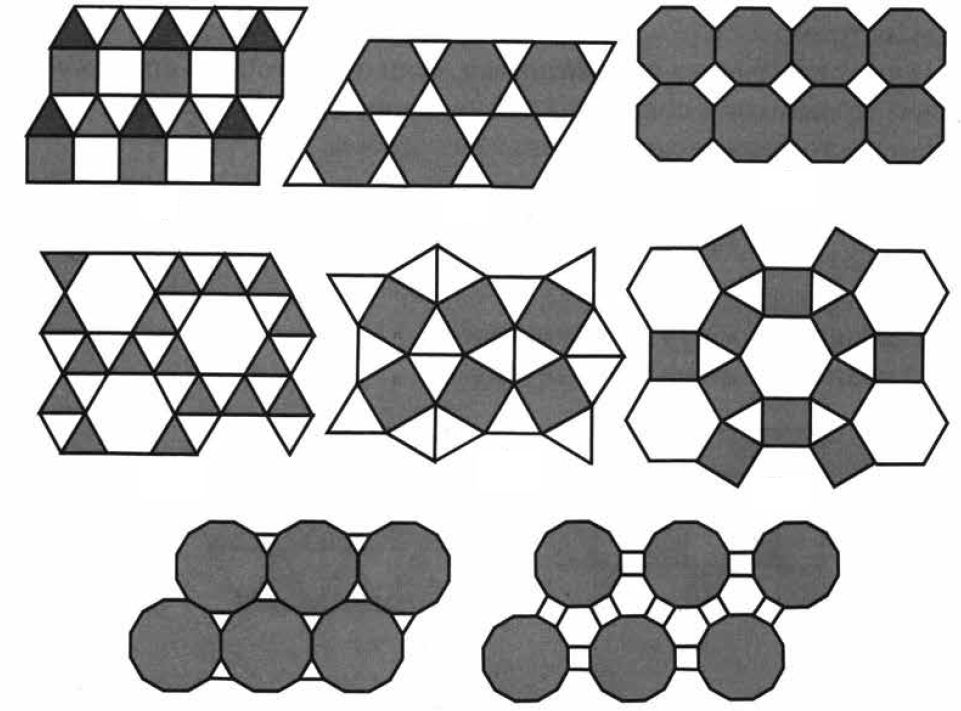
Рисунок 2 – Примеры паркетов из правильных многоугольников с разным числом сторон
И.Ф. Шарыгин описал паркет как плоские орнаменты, пополняющие лист бумаги (плоскость) без промежутков [2].
Некоторые определения паркета не ограничиваются многоугольниками. Так, например, определил паркет Мауриц Эшер – нидерландский художник, прославившийся благодаря своим орнаментальным гравюрам и работам с «невозможной архитектурой» [3].
Паркет – это орнамент, заполняющий лист бумаги (плоскость) без промежутков.
На рисунке 3 приведены паркеты М. Эшера, состоящие из фигур, заполняющих всю плоскость без наложений при параллельных переносах.




Рисунок 3 – Паркеты М. Эшера
Паркеты М. Эшера нашли свое воплощение в практической жизни людей. На рисунке 4 приведены интерьер, в котором полы выкладываются его паркетом, который называется «Ящерецы», и фрагмент напольной мозаики в аквапарке Севастополя «Черепашки». Это, конечно же, единичные примеры использования паркетов Эшера в интерьерах и экстерьерах. На самом деле, его работы довольно часто используются для украшения артобъектов, особенно в Европе.
У М. Эшера есть большое количество последователей. Работы некоторых из них приведены на рисунке 5.


Рисунок 4 – Паркеты М. Эшера в практической жизни

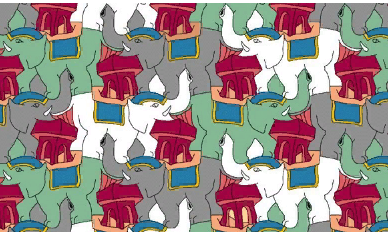



Рисунок 5 – Паркеты Yoshiaki Araki и Makoto Nakamura
Паркеты встречаются не только на плоскости. Примером паркета на сферической поверхности может являться обычный футбольный мяч (см. рисунок 6).



Рисунок 6 – Паркеты на поверхности сферы
1.2 Как знания о паркетах помогают делать открытия в физике и химии
Паркеты – это еще и двумерная кристаллография. До сих пор ученые открывают новые свойства паркетов и новые минералы, новые кристаллы, потому что строение кристаллов описывается структурой, которая составляет паркеты.
Так в 2010 году Нобелевская премия по физике присуждена Андрею Гейму и Константину Новоселову за открытие графена – двумерной формы углерода. Углерод – уникальных химический элемент, способный образовывать разнообразные химические структуры в виде одномерных цепочек, циклических образований и пространственных соединений. Благодаря этому многообразию обеспечивается функционирование генетических кодов всего живого на Земле [4]. На рисунке 7 размещено фото лауреатов Нобелевской премии 2010 года.

Рисунок 7. Лауреаты Нобелевской премии по физике за 2010 г. А. Гейм (слева), К. Новоселов (справа)
В 2011 году Нобелевскую премию в области химии присудили израильскому ученому Дэниэлю Шехтман за открытие квазикристаллов, формы которых в мозаике Пенроуса [5]. Роджер Пенроуз (британский физик и математик) решил задачу составления структуры паркета из нескольких видов многоугольников, покрывающую всю плоскость. При этом структура должна быть не совсем «правильной» или «почти» периодической. Р. Пенроуз использовал всего два вида ромбов. На рисунке 8 (слева) показан вариант квазипериодического (т.е. почти периодического) заполнения плоскости ромбами с острыми углами в 72 и 36°. Их еще называют «толстыми» и «худыми» ромбами. На этом же рисунке (справа) размещена фотография Д. Шахмана, обнаружившего первый квазикристалл – одну из форм организации структуры твердых тел.


Рисунок 8. Мозаика Пенроуса (слева). Д. Шахман – лауреат Нобелевской премии 2011 г.
1.3 Простейшие фигуры и движения для построения паркетов
Для построения паркетов авторы ограничились небольшим набором геометрических фигур и несколькими видами движений.
Самым простым элементом паркета является треугольник – геометрическая фигура, известная из курса начальной школы. Также в начальной школе изучены прямоугольник и квадрат.
Общее определение для используемых в паркетах фигур, построение которых выполнили авторы, – многоугольник.
Многоугольник – фигура, образованная замкнутой ломаной линией вместе с частью плоскости, ограниченной этой линией [7, с. 31].
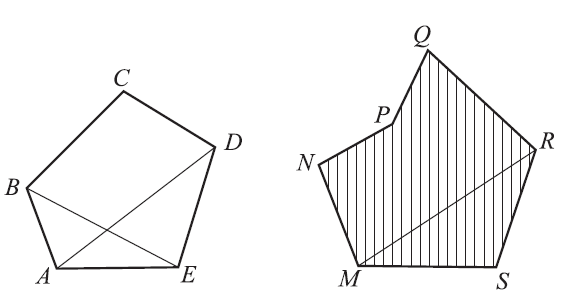
Рисунок 9 – Многоугольники
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны [7, с. 65]. Изображение параллелограмма помещено на рисунке 10.
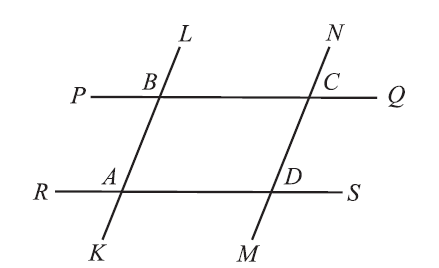
Рисунок 10 – Параллелограмм ABCD
Трапеция – четырехугольник, у которого две противоположные стороны параллельны, а две другие не параллельны [7, с. 71]. Изображение трапеции приведено на рисунке 11.
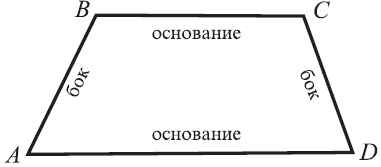
Рисунок 11 – Трапеция ABCD
Многоугольник называется правильным, если он ограничен правильной ломаной линией, т.е. если он имеет равные стороны и равные углы [7, с. 167]. На рисунке 12 приведены примеры правильных многоугольников: треугольник, четырехугольник, одиннадцатиугольник, шестиугольник, пятиугольник.
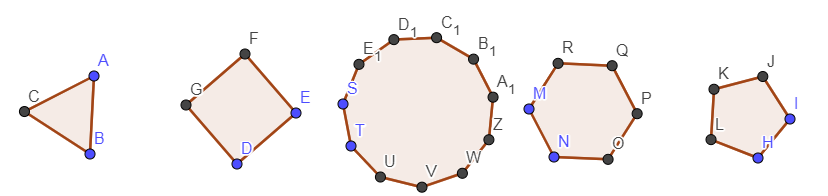
Рисунок 12 – Правильные многоугольники
Вектор (направленный отрезок) – отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом [8, с. 190]. На рисунке 13 изображен вектор 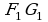 .
.
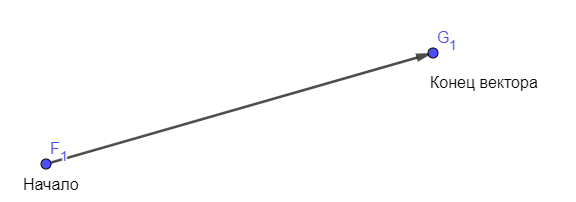
Рисунок 13 – Вектор 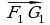
Движение (перемещение) – преобразование фигуры F, сохраняющее расстояние между точками [9, с. 160].
Гармонию и симметрию часто смешивают с красотой. Идею порядка и красоты воплощают два принципа: качественный принцип гармонии и количественный принцип симметрии. Уже древние греки отчетливо понимали основные функции гармонии как упорядочивающего начала. В древнегреческой философии гармония в противоположность хаосу означала организованность всей Вселенной. Гармония трактовалась как внутреннее единство, как единство противоположностей предела и беспредельного, частей и целого, мужского и женского, хорошего и дурного.
Понятия симметрии, пропорции и ритма играли важную роль в познании греками пространственно-временной структуры окружающего мира. Закономерность и красота мироздания раскрывались перед ними и в симметрии живых организмов, и в пропорциональном строении человека, и в ритмах чередования дня и ночи, смены времен года и т.д. [10, с. 88] На рисунке 14 приведено изображение Трона Людовизи (Рим, Около 460 года до н.э., Музей Терм. Рельеф передней стороны: рождение Афродиты. Это пример скульптуры, обладающей свойством симметрии.

Рисунок 14 – Рождение Афродиты
Греческое слово симметрия означает совместную меру, соразмерность [10, с. 95]. Симметрия пронизывает буквально все вокруг, захватывая, казалось бы, совершенно неожиданные области и объекты. Здесь уместно привести высказывание Дж. Ньюмена, который особенно удачно подчеркнул всеохватывающие и вездесущие проявления симметрии: «Симметрия устанавливает забавное и удивительное сродство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными: земным магнетизмом, женской вуалью, поляризованным светом, естественным отбором, теорией групп, инвариантами и преобразованиями, рабочими привычками пчел в улье, строением пространства, рисунками ваз, квантовой физикой, скарабеями, лепестками цветов, интерференционной картиной рентгеновских лучей, делением клеток морских ежей, равновесными конфигурациями кристаллов, романскими соборами, снежинками, музыкой, теорией относительности...» [11, с. 4].
Авторы уже имеют представление об осевой и центральной симметриях на плоскости. На рисунке 15 приведены примеры осевой и центральной симметрий в природе и рисунке.

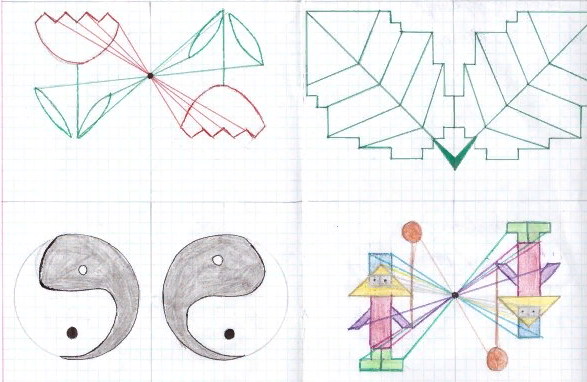
Рисунок 15 –Осевая и центральная симметрия
Симметрии бывают разными: от самых привычных и понятных до очень сложных. Симметрия трехмерного пространства представлена на рисунке 16 в виде кристалла алмаза (форма углерода) [12, с. 225], о котором говорили выше.
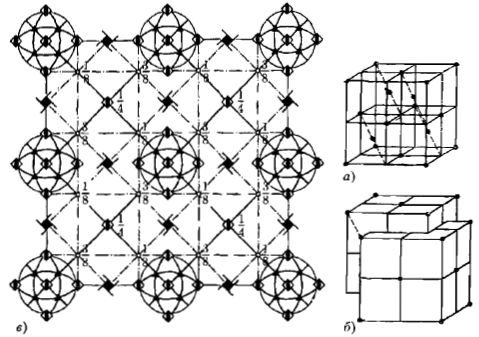
Рисунок 16 – Структура алмаза
Две фигуры называются симметричными относительно какой-либо точки O пространства, если каждой точке A одной фигуры соответствует в другой фигуре точка 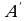 , расположенная на прямой OA по другую сторону от точки O, на расстоянии, равном расстоянию точки А от точки О. Точка О называется центром симметрии фигур (см. рисунок 17) [7, с. 279].
, расположенная на прямой OA по другую сторону от точки O, на расстоянии, равном расстоянию точки А от точки О. Точка О называется центром симметрии фигур (см. рисунок 17) [7, с. 279].
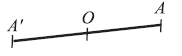
Рисунок 17 – Центральная симметрия
Симметрия осевая. Точки 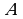 и
и 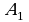 называют симметричными относительно прямой
называют симметричными относительно прямой 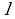 , если прямая
, если прямая 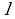 является серединным перпендикуляром отрезка
является серединным перпендикуляром отрезка 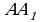 (см. рисунок 18). Если точка
(см. рисунок 18). Если точка 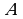 принадлежит прямой
принадлежит прямой 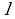 , то её считают симметричной самой себе относительно прямой
, то её считают симметричной самой себе относительно прямой 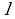 [9, с.168].
[9, с.168].
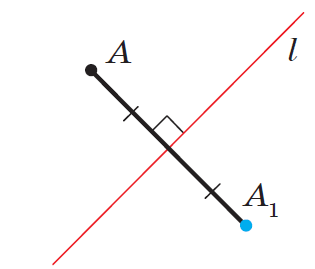
Рисунок 18 – Осевая симметрия
Параллельный перенос на вектор 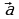 – отображение пространства на себя, при котором любая точка
– отображение пространства на себя, при котором любая точка 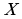 переходит в такую точку
переходит в такую точку 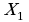 , что
, что 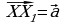 (см. рисунок 19) [9, с. 159].
(см. рисунок 19) [9, с. 159].
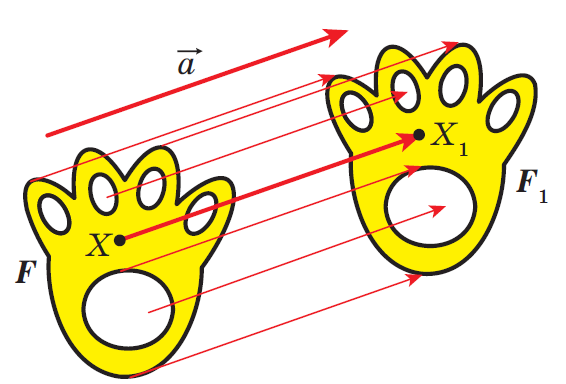
Рисунок 19 – Параллельный перенос фигуры F на вектор 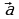
Поворот (радиальная симметрия) плоскости вокруг точки О на угол 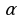 Точки
Точки 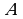 и
и 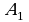 называют симметричными относительно точки О, если точка О является серединой отрезка
называют симметричными относительно точки О, если точка О является серединой отрезка 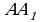 называется отображение плоскости на себя, при котором точка
называется отображение плоскости на себя, при котором точка 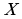 переходит в такую точку
переходит в такую точку 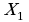 , что
, что 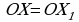 , и угол
, и угол 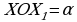 (см. рисунок 20) [8, с.294].
(см. рисунок 20) [8, с.294].
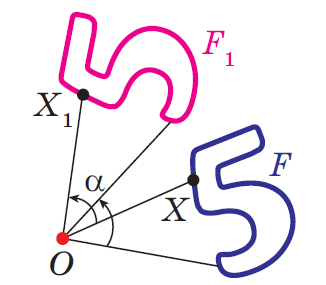
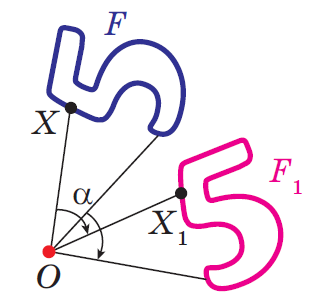
Рисунок 20 – Поворот вокруг точки О против часовой стрелке и по часовой стрелке
1.4 Примеры построения паркетов
На рисунках 21 и 22 показаны простые способы построения паркетов с помощью простых преобразований.
Так «Хор моряков» составил шестиклассник Б. Сторонкин. За основу он взял квадрат 3*3 клетки. Верхнюю часть квадрата изменил как на рис. а). Чтобы ячейки «вдвинулись» одна в другую, так же изменил и противоположную сторону. К левой стороне квадрата пририсовал треугольник. Такой же треугольник вырезан и с противоположной стороны. Получилась ячейка. Далее он разрисовал ее так, как показано на рисунке б). Составляя одинаковые ячейки одну за другой, получим соответственный паркет [2, c. 146].
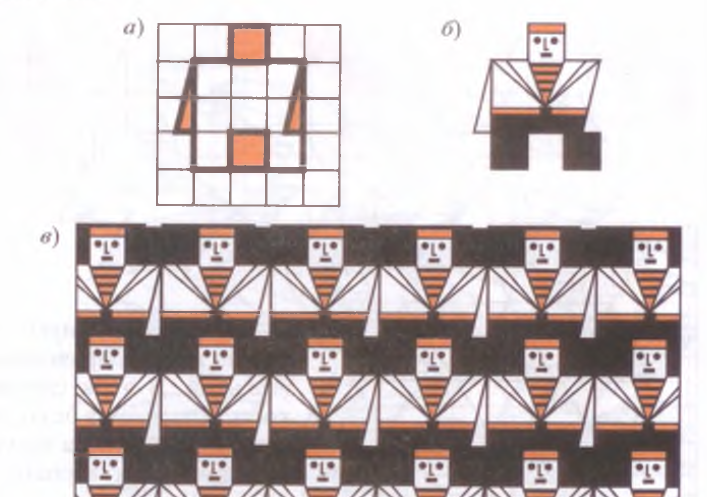
Рисунок 21 – Паркет «Хор моряков»
По тому же принципу построены более сложные паркеты «Ящерицы» и «Две птицы» М. Эшера (см. рисунок 22).
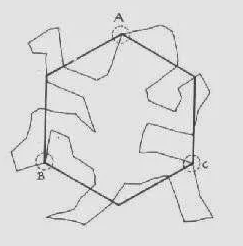
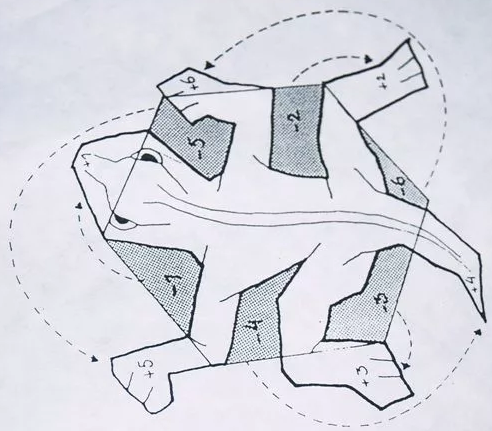
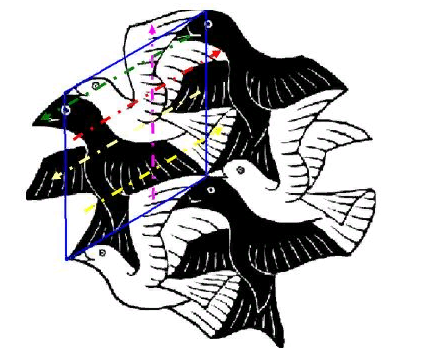
Рисунок 22 – Построение паркетов М. Эшера
Таким образом, заключаем, что построение паркетов основано на знаниях геометрии. Чаще всего для их построения используют простые геометрические формы и преобразования (движения). Школьнику вполне доступно составление авторских паркетов. Глубокое изучение паркетов позволяет ученым делать важные для современности открытия.
Практическая часть
2.1 Динамическая среда GeoGebra
Программа GeoGebra написана Маркусом Хохенвартером на языке Java и работает на большом числе операционных систем. Переведена на 39 языков и в на-стоящее время активно разрабатывается. Полностью поддерживает русский язык.
В июне 2013 года впервые в истории российских научно-методических журналов вышел специальный выпуск Европейского журнала современного образования, посвящённый использованию GeoGebra в учебном процессе.
Назначение и функционал программы GeoGebra
GeoGebra – это бесплатная математическая программа, которая включает в себя алгебру, геометрию, таблицы, статистику, арифметику и т.д. Все разделы синхронизируются между собой и связаны динамически в один пакет. Благодаря большому количеству вычислительных действий приложение поможет в проведении различных математических операций для решения практически любых примеров и задач. GeoGebra предназначена для всех уровней образования, удобна в использовании благодаря простому интерфейсу и наличию локализации на русском языке.
Примечательно, что все разделы взаимосвязаны между собой, что значительно облегчает работу c вычислениям. Программа отлично подойдет для решения разного уровня задач, включая сложные геометрические задачи и простые арифметические примеры.
Список возможностей GeoGebra – действительно обширный и к ним можно отнести следующие:
создание чертежей, содержащих геометрические фигуры (круги, многоугольники, точки, прямые),
вычерчивание графиков функций на основе уравнений или наборов данных,
настройка диаграмм (тип и размер линии, цвет, подписи осей, масштабирование),
измерение углов и расстояния между фигурами,
возможность применения преобразований и геометрических конструкций,
создание чертежей трехмерных тел в трех измерениях, в том числе расчет значений углов в пространстве, построение сечений и сеток,
работать в векторах,
решение систем уравнений и неравенств,
расчет производных функции,
три режима представления: графический, алгебраический, таблицы,
поддержка пользовательских типов инструментов,
условные операторы и динамическое создание цветов,
поддержка нескольких слоев,
экспорт результатов работы в графический формат (PNG, HTML, PDF, SVG) [13].
2.2 Построение паркетов в GeoGebra
Паркет из треугольников
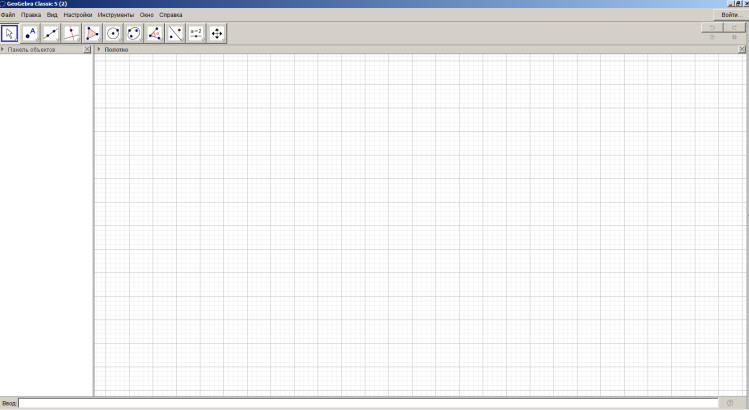
Рисунок 23 – Подготовка поля для построения паркета
В динамической среде GeoGebra строим с помощью инструмента «Многоугольник» произвольный треугольник.
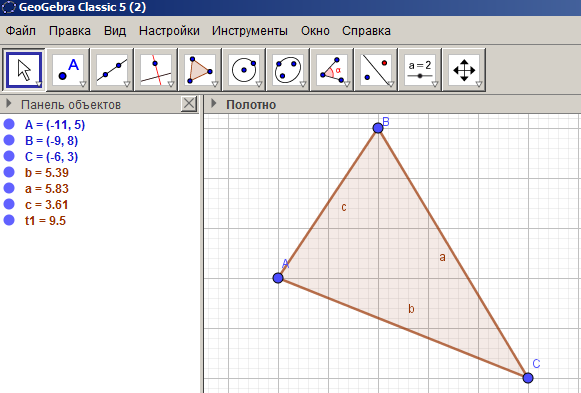
Рисунок 24 – Элемент для построения паркета
Найдем середину отрезка BC с помощью инструмента Середина или центр. Достроим треугольник до параллелограмма путем центральной симметрии относительно середины отрезка BC с помощью инструмента «Отражение относительно точки» (см. рисунок 25). Последовательно треугольник ABC многократно отобразим с помощью параллельного переноса на вектор AC, а треугольник 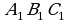 на вектор
на вектор 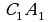 . Получаем фрагмент, состоящий из двух параллелограммов (см. рисунок 25). Продолжая подобные перемещения двух первоначально построенных треугольников на векторы AB и
. Получаем фрагмент, состоящий из двух параллелограммов (см. рисунок 25). Продолжая подобные перемещения двух первоначально построенных треугольников на векторы AB и 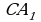 получаем следующий фрагмент, состоящий из трех параллелограммов.
получаем следующий фрагмент, состоящий из трех параллелограммов.
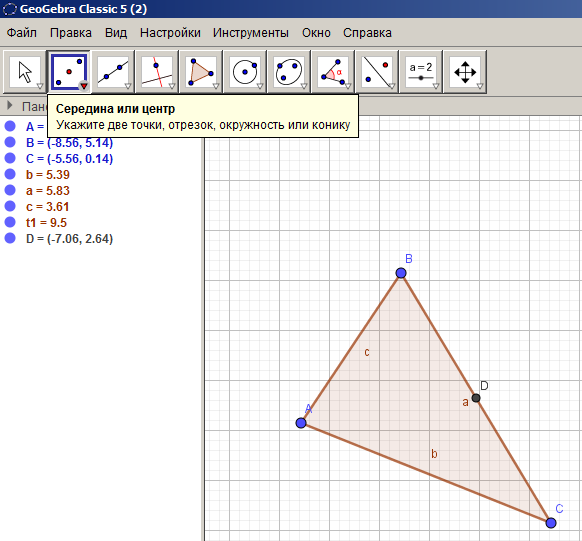
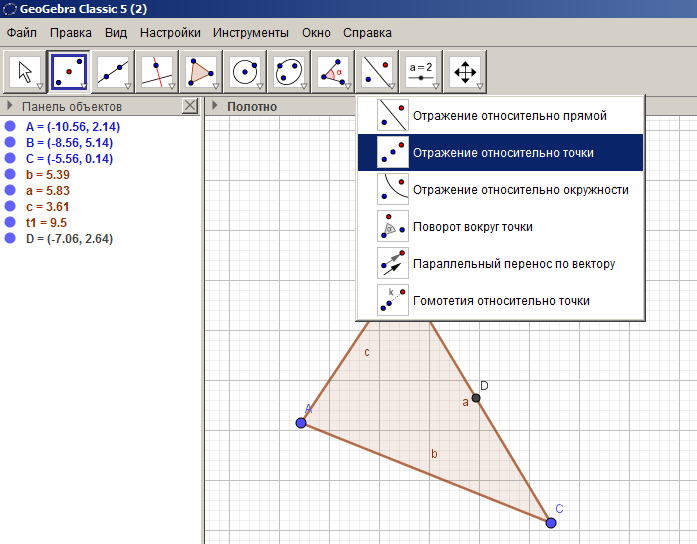
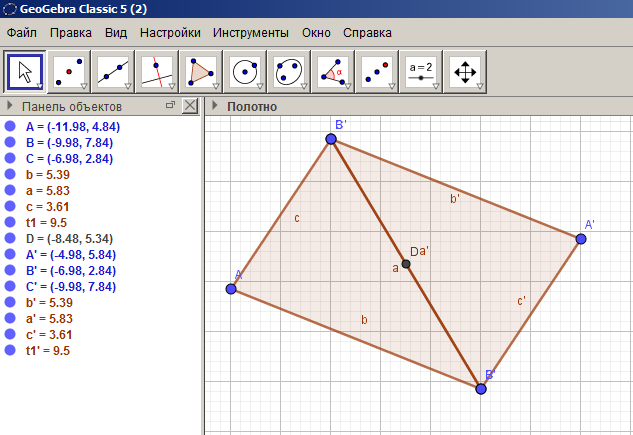
Рисунок 25 – Нахождение середины отрезка и симметрия относительно точки D
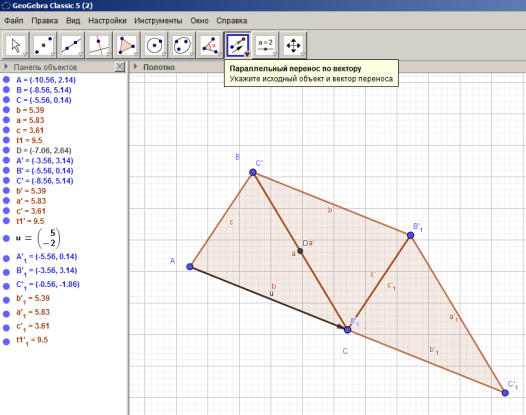
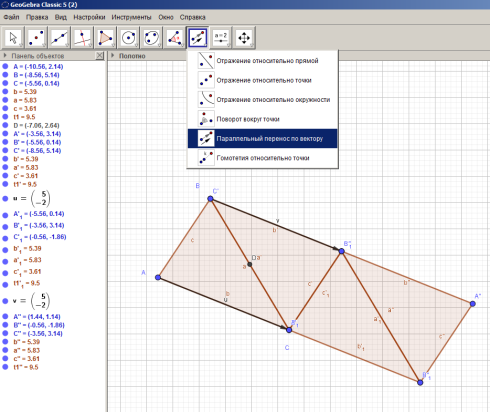
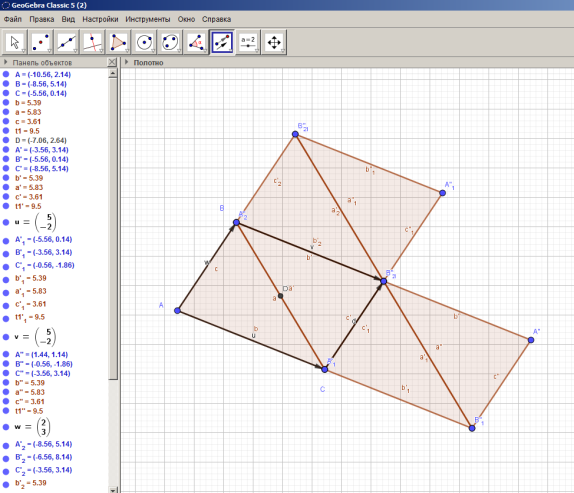
Рисунок 26 – Построение паркета из треугольников
Аналогично выполняется построение паркетов из параллелограммов, трапеций, шестиугольников. Результаты построений приведены на рисунках 27-29.
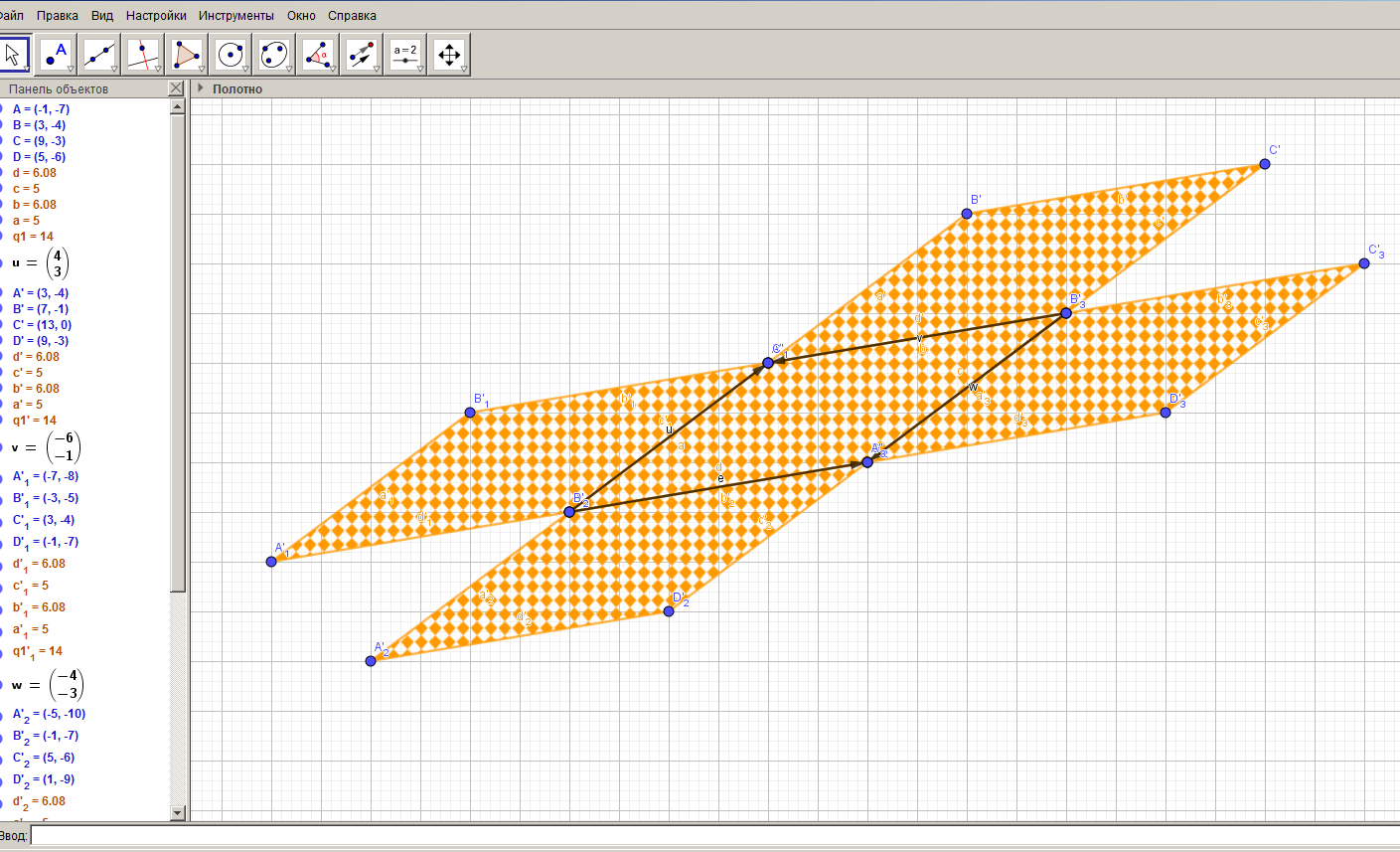
Рисунок 27 – Паркет, составленный из параллелограммов
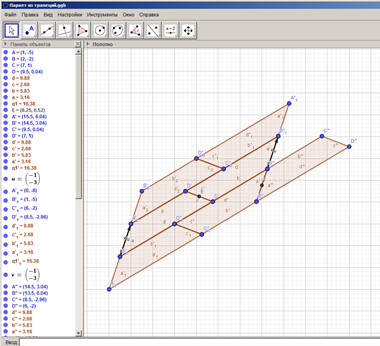
Рисунок 28 – Паркет, составленный из трапеций
Для построения паркета из правильных шестиугольников потребовалось умение выполнять поворот шестиугольника относительно его вершин на угол 120 градусов.
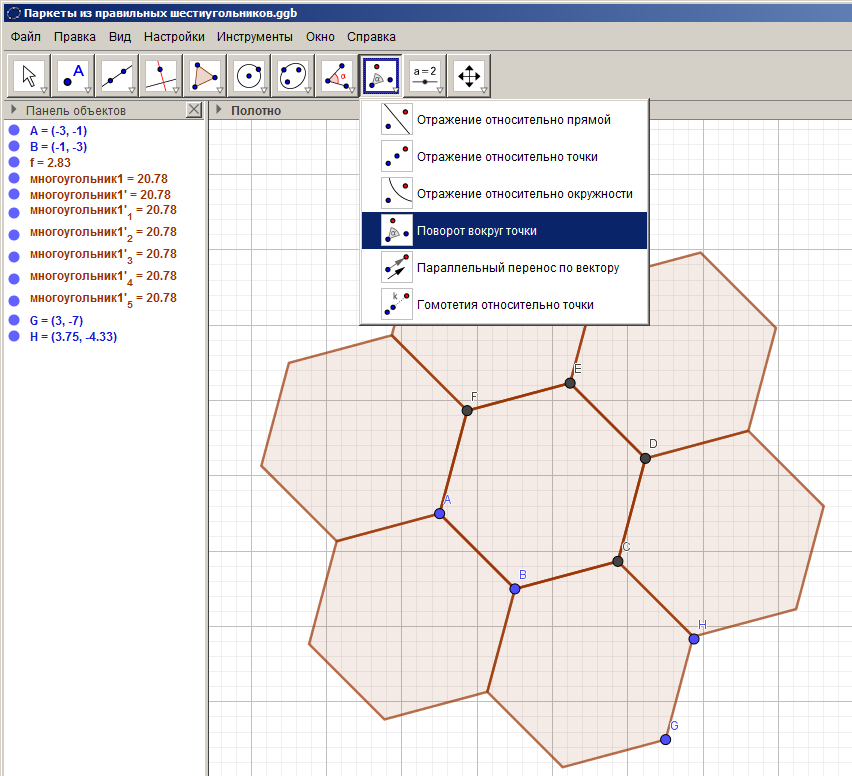
Рисунок 29 – Паркет, составленный из правильных шестиугольников
В процессе работы над этими паркетами убедились, что с помощью GeoGebra возможно строить разнообразные по форме, цвету, стилю паркеты.
Заключение
Целью проведения учебного исследования было формирование представлений о том, что такое паркеты, какими они бывают, как они составляются и где применяются.
Для достижения цели были поставлены ряд задач: изучить и выбрать для написания работы информационные источники по теме «Паркеты»; сформировать представление о паркете, его видах и способах построения; изучить несложные плоские геометрические фигуры (правильный многоугольник, четырехугольник и его виды, некоторые виды преобразований плоскости); научиться с помощью графической системы GeoGebra строить паркеты.
Нехватка знаний по геометрии перед началом работы заставила самостоятельно изучить некоторые темы, такие как «Многоугольники», «Движение», «Векторы». Также для решения последней поставленной задачи пришлось изучать руководство по работе с программой GeoGebra. Пришлось много экспериментировать для получения фрагментов паркетов, составленных из простых плоских фигур (треугольников, параллелограммов, трапеций, шестиугольников). В ходе экспериментов был сделан вывод о том, что не из любых правильных многоугольников можно составить паркет. Это можно сделать, сочетая несколько видов многоугольников. Работа над составлением паркетов оказалась нелегкой, но увлекательной. Принято решение о продолжении исследования данной темы, построении более сложных и разнообразных паркетов на бумаге и в GeoGebra.
Работая над темой, стало интересно выяснить, какими паркетами украшены улицы и площади нашего города. Оказалось, что в оформлении города нет большого разнообразия. В основном, площади, тротуары и дворы выложены образцами, которые можете видеть в приложении.
В итоге, все поставленные задачи последовательно решены, цель достигнута.
Список использованных источников
Смирнов В.А., Смирнова И.М., Ященко И.В. Наглядная геометрия. – М.: МЦНМО, 2013. –272 с.
Шарыгин И.Ф. Математика: наглядная геометрия. 5-6 кл.: учебник/ И.Ф. Шарыгин, Л.Н. Ерганжиева. – 2-е изд., стереотип. –М.: Дрофа, 2015. –189 с.
Мауриц Корнелис Эшер: произведения и биография. [Электронный ресурс]. Режим доступа: https://artchive.ru/escher (дата обращения 11.03.2022)
Ерин Ю. Нобелевская премия по физике – 2010. [Электронный ресурс]. Сайт Новости науки на «Элементах». Режим доступа: https://elementy.ru/novosti_nauki/431427/Nobelevskaya_premiya_po_fizike_2010 (дата обращения 06.03.2022)
Агамбердиев Ш. Мозаика Пенроуза, или как среднеазиатские зодчие на пять веков предвосхитили открытие европейских учёных –/ [Электронный ресурс]. Сайт Письма о Ташкенте. Режим доступа: https://mytashkent.uz/2018/12/29/mozaika-penrouza/ (дата обращения 08.03.2022)
Израильская премия за кристаллы. [Электронный ресурс]. Сайт Газета.ру. Режим доступа: https://www.gazeta.ru/science/2011/10/05_a_3790714.shtml (дата обращения 07.03.2022)
Киселев А.П. Геометрия / под ред. Н.А Глаголева. –М.: ФИЗМАТЛИТ, 2013. –328 С.
Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 2-е изд. – М.: Просвещение, 2014. – 383 с.
Мерзляк А. Г. Геометрия : учеб. для 9 кл. общеобразоват. учеб. заведений с обуч. на рус. яз. : пер. с укр. / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. – Х. : Гимназия, 2017. – 240 с.
Волошинов А.В. Математика и искусство: Кн. Для тех, кто не только любит математику и искусство, но и желает задуматься о природе прекрасного и красоте науки. – 2-е изд., дораб и доп. –М.: Просвещение, 2000. –399 с.
Вернер Гильде. Зеркальный мир. Перевод с немецкого канд. геол.-мин. наук Т. Б. Здорик и канд. геол.-мин. наук Л. Г. Фельдмана под редакцией д-ра геол.-мин. наук проф. И. И. Шафрановского, МОСКВА, «МИР», 1982.
Шубников А.В., Копцик В.А. Симметрия в науке и искусстве. –Москва-Ижевск: Институт компьютерных исследований, 2004. – 560 с.
Руководство — GeoGebra Руководство. [Электронный ресурс]. Сайт WikipediA. Режим доступа: https://wiki.geogebra.org/ru/Руководство (дата обращения 08.03.2022)
Приложение
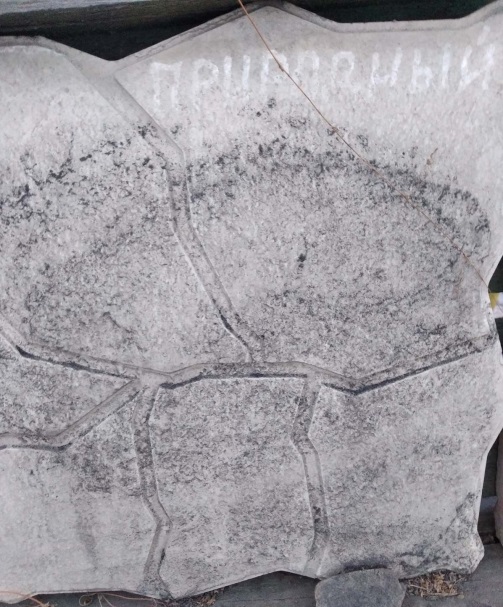
Паркеты Абакана
В основном, площади, тротуары и дворы города Абакана выложены образцами паркетов, которые можете видеть ниже. Их изготавливают местные предприниматели. Они не отличаются особым многообразием, но при этом, удобны в эксплуатации.






Продолжение приложения

































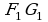 .
.
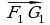




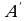 , расположенная на прямой OA по другую сторону от точки O, на расстоянии, равном расстоянию точки А от точки О. Точка О называется центром симметрии фигур (см. рисунок 17) [7, с. 279].
, расположенная на прямой OA по другую сторону от точки O, на расстоянии, равном расстоянию точки А от точки О. Точка О называется центром симметрии фигур (см. рисунок 17) [7, с. 279]. 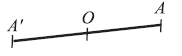
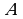 и
и 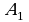 называют симметричными относительно прямой
называют симметричными относительно прямой 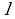 , если прямая
, если прямая 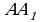 (см. рисунок 18). Если точка
(см. рисунок 18). Если точка 
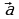 – отображение пространства на себя, при котором любая точка
– отображение пространства на себя, при котором любая точка 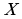 переходит в такую точку
переходит в такую точку 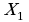 , что
, что 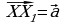 (см. рисунок 19) [9, с. 159].
(см. рисунок 19) [9, с. 159].
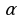 Точки
Точки 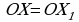 , и угол
, и угол 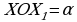 (см. рисунок 20) [8, с.294].
(см. рисунок 20) [8, с.294]. 







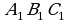 на вектор
на вектор 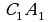 . Получаем фрагмент, состоящий из двух параллелограммов (см. рисунок 25). Продолжая подобные перемещения двух первоначально построенных треугольников на векторы AB и
. Получаем фрагмент, состоящий из двух параллелограммов (см. рисунок 25). Продолжая подобные перемещения двух первоначально построенных треугольников на векторы AB и 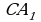 получаем следующий фрагмент, состоящий из трех параллелограммов.
получаем следующий фрагмент, состоящий из трех параллелограммов. 





























