Перемещения при изгибе

Перемещения при изгибе

Перемещение центра тяжести сечения по направлению перпендикулярному к оси балки, называется прогибом . Прогиб обозначается буквой w

Наибольший прогиб в пролете или на консоли балки, называется стрелой прогиба и обозначается буквой f .

Угол,  , на который каждое сечение поворачивается по отношению к своему первоначальному положению и есть угол поворота .

Угол поворота сечения равен значению производной от прогиба по координате Z в этом же сечении, то есть:

Уравнение упругой линии балки

Метод непосредственного интегрирования

Значения постоянных интегрирования С и D определяют из начальных условий на опорах балки

Уравнение упругой линии балки

Метод Клебша

Для составления уравнений необходимо выполнить следующие основные условия:

• начало координат, для всех участков, необходимо расположить в крайнем левом конце балки;
• интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
• при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на ( Z - a ) 0 где а - координата сечения, в котором приложен момент;
• в случае обрыва распределенной нагрузки ее продлевают до конца балки, а для восстановления действительных условий нагружения вводят «компенсирующую» нагрузку обратного направления

Уравнение упругой линии балки

Метод начальных параметров

Где  —угол поворота сечения, w —прогиб,  0 - угол поворота в начале координат, w 0 — прогиб в начале координат , d i — расстояние от начало координат до i -той опоры балки, a i — расстояние от начало координат до точки приложения сосредоточенного момента M i , b i — расстояние от начало координат до точки приложения сосредоточенной силы Fi , с i— расстояние от начало координат до начала участка распределенной нагрузки q i , R i и М р i — реакция и реактивный момент в опорах балки.

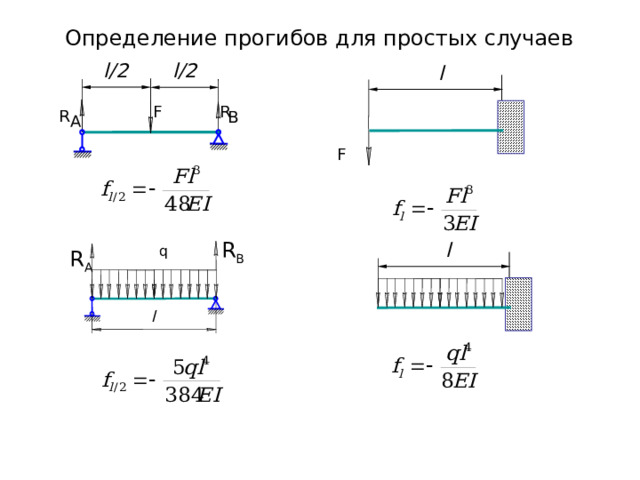
Определение прогибов для простых случаев

l/2

l/2

l

F

R

R

B

A

F

R В

l

q

R A

l