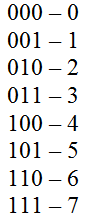Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и наоборот

Тема: "Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и наоборот".

Цель работы: 

Получение практических навыков преобразования чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и наоборот.

Количество часов на выполнение работы

Продолжительность выполнения данной практической работы составляет 2 академических часа.

Оборудование

• тетрадь;

• ручка (карандаш);

• калькулятор.

Краткие теоретические сведения

Система счисления – совокупность приемов и правил для обозначения и наименования чисел. Системы счисления подразделяются на позиционные (десятичная, двоичная, восьмеричная, шестнадцатеричная) и непозиционные (римская система счисления).

Алфавит системы счисления – множество всех символов (знаков), используемых для записи чисел в данной системе счисления.

Система счисления называется непозиционной, если количественный эквивалент значения любого символа не зависит от его положения (позиции) в коде числа.

Пример: Римская система счисления (2,5тыс. лет до н.э.) 1 -I, 10 - Х, 100 -C, 1000 -M, 5 -V, 50 -L, 500 -D

Для записи числа его раскладывают на сумму цифр 1000, 500, 100, 50, 10, 5, 1.

Система счисления называется позиционной, если количественный эквивалент (значение символа) зависит от его положения в записи числа.

Базисом позиционной системы счисления называется последовательность чисел, каждое из которых определяет количественный эквивалент (вес) символа в зависимости от его места в коде числа.

Основанием позиционной системы счисления называется целое число, которое возводится в степень для получения базиса. Основание в позиционной системе счисления показывает, во сколько раз изменяется вес цифры при перемещении ее на соседнюю позицию. За основание системы счисления можно принять любое натуральное число n (n=1 - недопустимо, т.к. получим унарную систему счисления).

Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводить числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

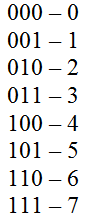
Рисунок 1 – Восьмеричная система счисления

Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями.

Например: 1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

Это значит, что число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 1011101₂ = 135₈.

Обратный перевод. Допустим, требуется перевести число 100₈ (100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.

100₈ = 1 0 0 = 001 000 000 = 001000000 = 1000000₂

Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме: 672₈ = 6 * 8² + 7 * 8¹ + 2 * 8⁰ = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 442₁₀.

Перевод десятичного числа в восьмеричное происходит делением этого числа на основание системы счисления 8.

Шестнадцатеричная система счисления – позиционная система счисления по основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F , то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

Рисунок 2 – Шестнадцатеричная система счисления

Это значит, что число 10101110110111 в двоичной системе счисления равно числу 2ВВ7 в шестнадцатеричной системе счисления. Или 10101110110111₂ = 2ВВ7₁₆.

Обратный перевод и перевод в десятичную систему происходит по тем же правилам, что и в восьмеричной системе счисления.

Задания по практической работе

1. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1101011₂, 10001011110₂, 461₈, 2644₈, 510₁₀, 1975₁₀, 3DF₁₆, 1A0A₁₆.

2. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1001110₂, 11000111011₂, 317₈, 3710₈, 252₁₀, 3999₁₀, 80C₁₆, 2FF2₁₆.

3. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1101100₂, 11001100110₂, 363₈, 4114₈, 515₁₀, 2345₁₀, 5АЕ₁₆, 3ВВС₁₆.

4. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1000111₂, 11100011011₂, 415₈, 3111₈, 260₁₀, 2901₁₀, A07₁₆, 9AA4₁₆.

5. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1101010₂, 10000011110₂, 333₈, 2077₈, 131₁₀, 3222₁₀, 77F₁₆, 5D74₁₆.

Контрольные вопросы

1. Что такое система счисления?

2. Какие системы счисления называются непозиционными?

3. Что такое основание, алфавит и базис системы счисления?

4. По какому правилу осуществляется перевод чисел из двоичной системы в восьмеричную, десятичную и шестнадцатеричную и наоборот?