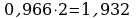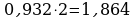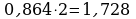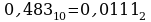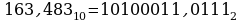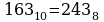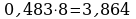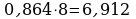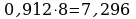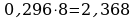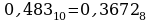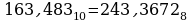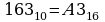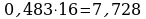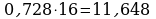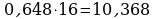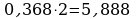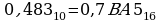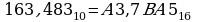Практическая работа
Перевод чисел из одной позиционной системы счисления в другую
Цель: научится переводить из одной позиционной системы счисления в другую.
Оборудование, программное обеспечение: ПК, ОС Windows.
Теоретические сведения
Система счисления или нумерация – это способ записи (обозначения) чисел.
Различают непозиционные и позиционные системы счисления.
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения этой цифры в числе.
Примером непозиционной системы, которая сохранилась до наших дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежали знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две скрещённые ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 стали применять первые буквы соответствующих латинских слов (centum — сто, demimille — половина тысячи, mille — тысяча).
Чтобы записать число, римляне разлагали его на сумму тысяч (М), полутысяч (D), сотен (С), полусотен (L), десятков (X), пятёрок (V), единиц (I). Например, десятичное число 128 представляется следующим образом:
CXXVIII = 100 + 10 + 10 + 5 + 1 + 1 + 1
(одна сотня, два десятка, пять, три единицы).
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (места, позиции) в записи числа.
Существует бесконечно много позиционных систем счисления. Каждая из них определяется целым числом q 1, называемым основанием системы счисления. Основание определяет (даёт) название системы счисления: двоичная, троичная, восьмеричная, шестнадцатеричная, q -ичная и т. д. Можно говорить «система счисления с основанием q» (табл. 1).
Основное достоинство любой позиционной системы счисления — возможность записи произвольного числа ограниченным количеством символов. Для записи чисел в позиционной системе счисления с основанием q нужен алфавит из q цифр: 0, 1, 2, ..., q - 1.
Представления чисел в системах счисления
Таблица 1
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | А |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Для перевода целого десятичного числа в систему счисления с основанием q следует:
1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.
Для перевода конечной десятичной дроби в систему счисления с основанием q следует:
1) последовательно умножать данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа;
2) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Пример. Рассмотрим примеры перевода десятичного числа 163,483 в 2-ичную, 8-ричную и 16-ричную системы счисления.
Решение
Переведем целую часть числа 163,483 в 2-ичную систему счисления
| _163 | 2 |
|
|
|
|
|
|
|
| 162 | _81 | 2 |
|
|
|
|
|
|
| 1 | 80 | _40 | 2 |
|
|
|
|
|
| 
| 1 | 40 | _20 | 2 |
|
|
|
|
|
|
| 0 | 20 | _10 | 2 |
|
|
|
|
|
|
| 0 | 10 | _5 | 2 |
|
|
|
|
|
|
| 0 | 4 | _2 | 2 |
|
|
|
|
|
|
| 1 | 2 | _1 | 2 |
|
|
|
|
|
|
| 0 | 0 | 0 |
|
|
|
|
|
|
|
| 1 |
|
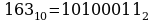
Переведем десятичную дробь 0,483 в 2-ичную систему счисления
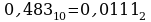
Ответ: 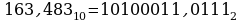
Переведем целую часть числа 163,483 в 8-ичную систему счисления
| _163 | 8 |
|
|
| 160 | _20 | 8 |
|
| 3 | 16 | _2 | 8 |
|
| 4 | 0 | 0 |
|
|
| 2 |
|
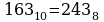
Переведем десятичную дробь 0,483 в 8-ичную систему счисления
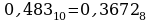
Ответ: 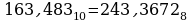
Переведем целую часть числа 163,483 в 16-ичную систему счисления
| _163 | 16 |
|
| 160 | _10 | 16 |
| 3 | 0 | 0 |
| 
| 10 (А)
| |
|
|
|
|
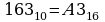
Переведем десятичную дробь 0,483 в 16-ичную систему счисления
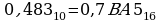
Ответ: 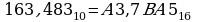
Содержание работы
ЗАДАНИЕ 1. Переведите числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления. Решение и ответ записать в тетрадь. Вариант спросите у преподавателя.
Вариант 1
а) 948;
б) 994,125;
в) 203,82.
Вариант 2
а) 563;
б) 234,25;
в) 286,16.
ЗАДАНИЕ 2. Сделать вывод о проделанной практической работе.







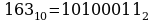

 (0)
(0)