Перпендикуляр и наклонная. Теорема о трех перпендикулярах.

19.12.2018 Расстояние от точки до плоскости. Теорема о трех перпендикулярах.

Урок геометрии в 10 классе

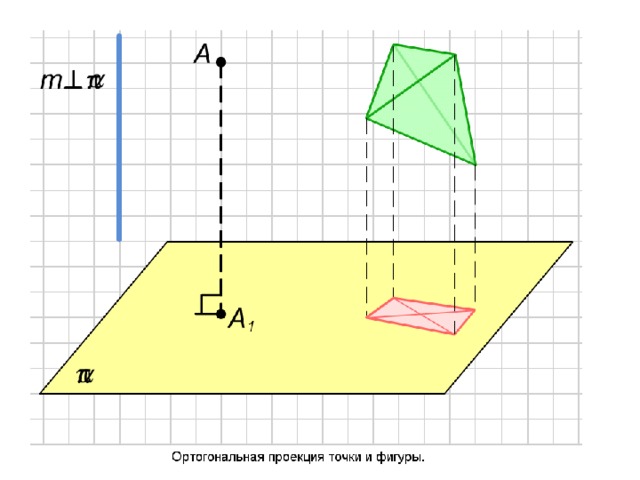
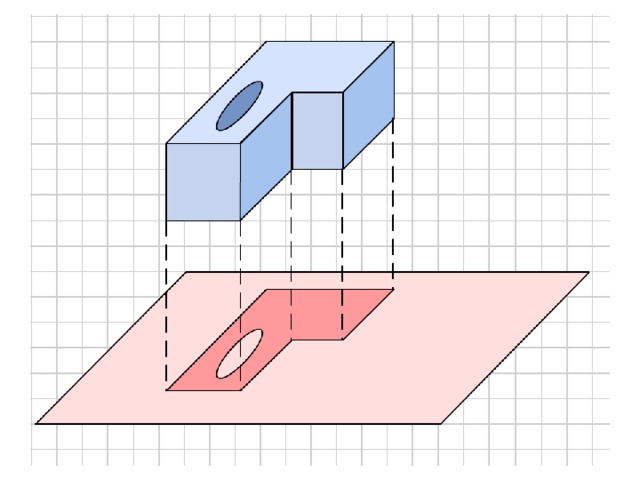
Перпендикуляр и наклонная

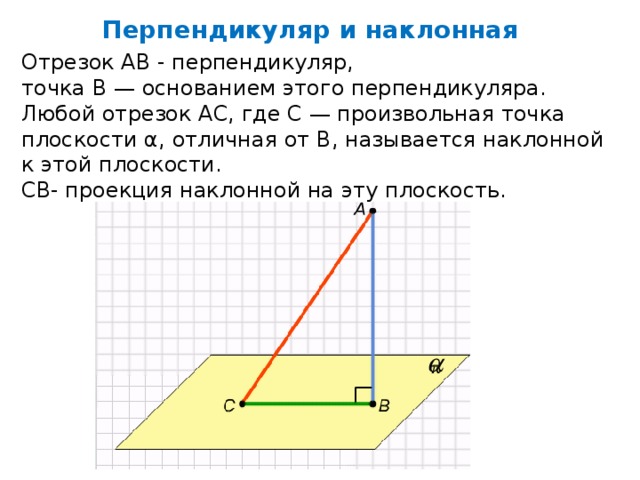
Отрезок АВ - перпендикуляр,

точка В — основанием этого перпендикуляра.

Любой отрезок АС, где С — произвольная точка плоскости α, отличная от В, называется наклонной к этой плоскости.

CB- проекция наклонной на эту плоскость.

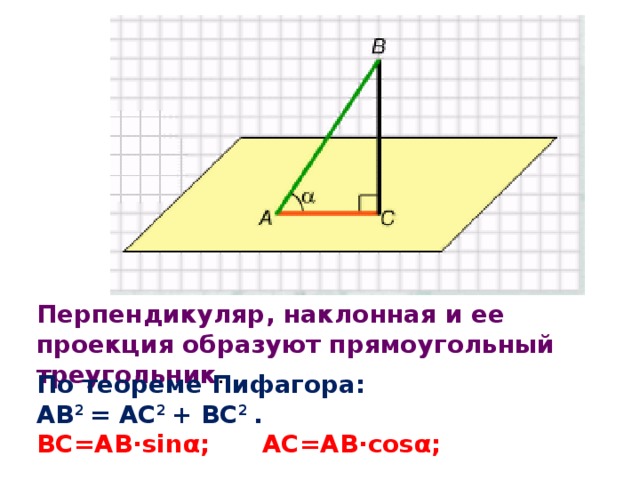
Перпендикуляр, наклонная и ее проекция образуют прямоугольный треугольник .

По теореме Пифагора:

АВ 2 = АС 2 + ВС 2 .

ВС=АВ∙sin α; AС=АВ∙cos α;

Свойства проекции

1. Перпендикуляр , проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.

2. Если наклонные равны, то равны и их проекции;

3. Если проекции наклонных равны, то равны и наклонные;

4. Если наклонные не равны, то большая наклонная имеет и большую проекцию.

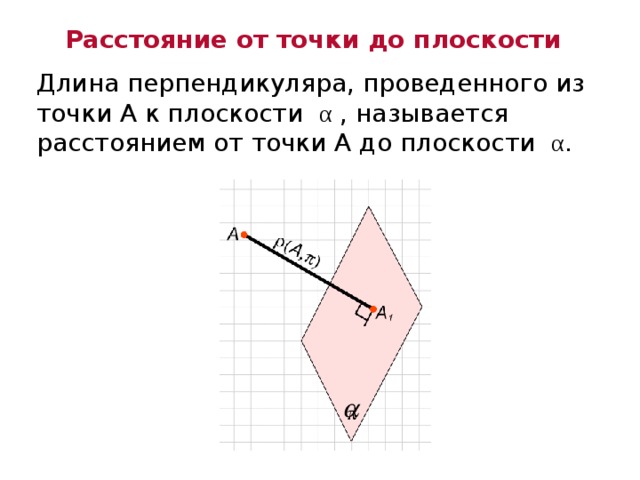
Расстояние от точки до плоскости

Длина перпендикуляра, проведенного из точки А к плоскости α , называется расстоянием от точки А до плоскости α .

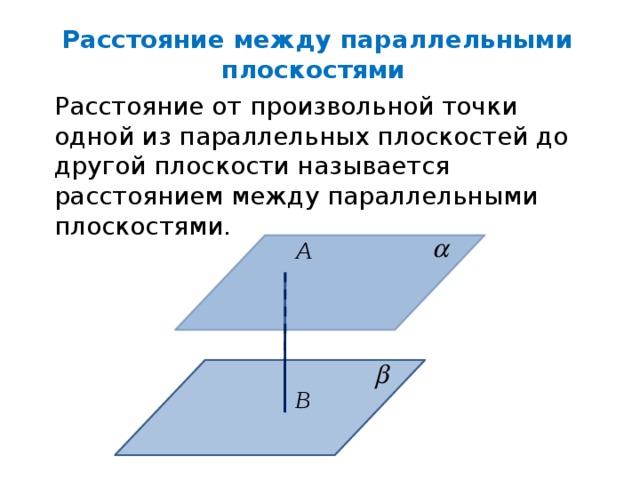
Расстояние между параллельными плоскостями

Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.

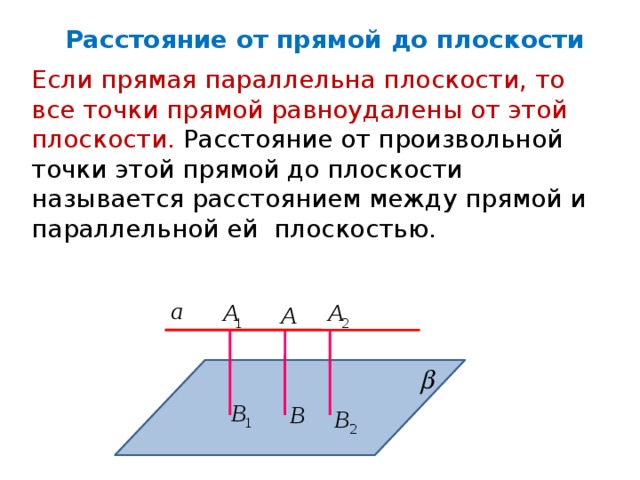
Расстояние от прямой до плоскости

Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. Расстояние от произвольной точки этой прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.

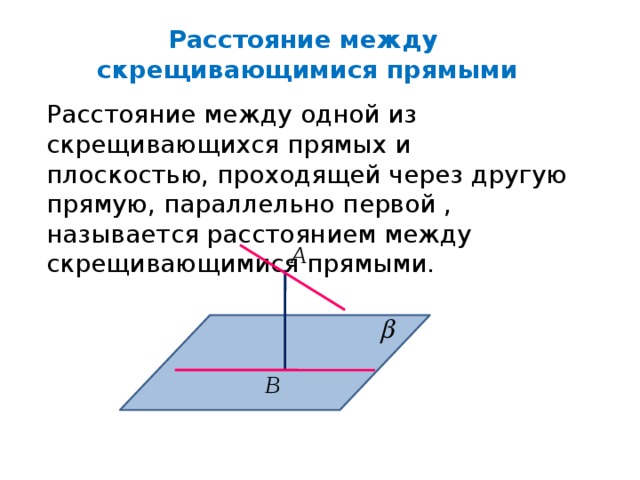
Расстояние между

скрещивающимися прямыми

Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую, параллельно первой , называется расстоянием между скрещивающимися прямыми.

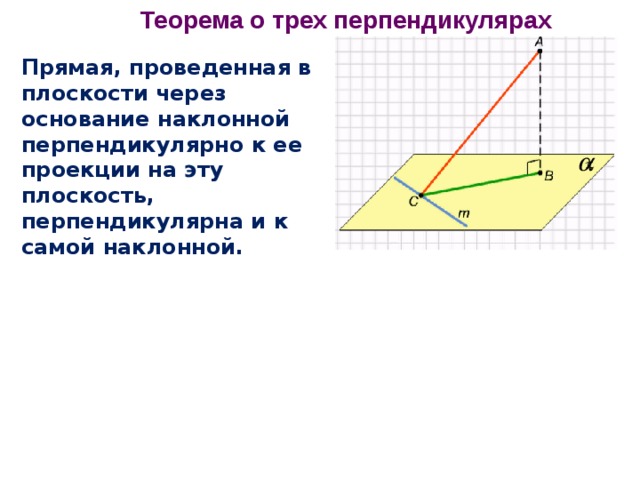
Теорема о трех перпендикулярах

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

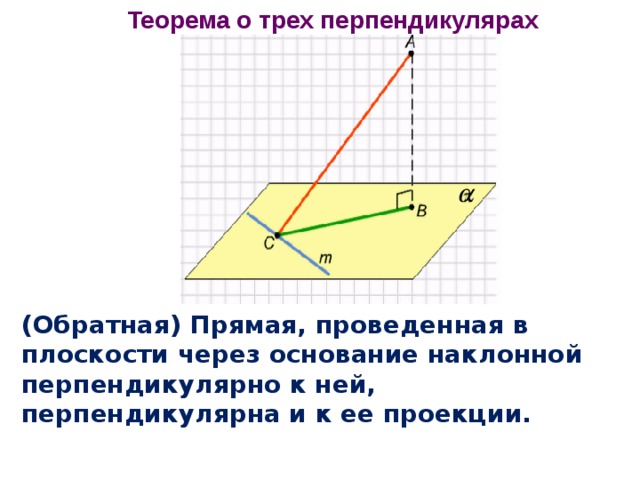
Теорема о трех перпендикулярах

(Обратная) Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

Домашнее задание:

№ 153, 144. пункты: 19-20.