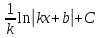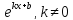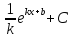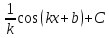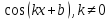Просмотр содержимого документа
«"Первообразная и интеграл"»
М-11
Тема урока
Неопределенный интеграл
Основные цели:
Образовательные цели:
знать
Определение неопределенного интеграла
Основное свойство неопределенного интеграла
уметь
Находить первообразные основных функций
Находить неопределенный интеграл
Развивающие цели:
1. Развитие вычислительного навыка.
2. Привитие навыка самостоятельной работы.
Воспитательные цели:
Развитие ответственного отношения к учебе.
Задачи урока
- ввести понятие неопределенного интеграла
- отработать навыки использования свойств неопределенного интеграла их
при решении заданий
Ход урока
Организационный момент
Мотивация учебной деятельности.
Тема сегодняшнего занятия «Неопределенный интеграл и его свойства». Знания по данной теме нами будет использоваться на следующих уроках при нахождении определенных интегралов, площадей плоских фигур. Большое внимание уделяется интегральному исчислению в разделах высшей математики в высших учебных заведениях при решении прикладных задач.
Презентация – слайды 1-11
Актуализация знаний
- повторить понятие первообразой (слайд 12)
- теорему о множестве первообразных (слайд 13 - 14)
- таблицу первообразных (слайды 15-16)
Изучение нового материала
Операция интегрирования обратная операции дифференцирования, т.е. для того, чтобы проверить правильность нахождения интеграла необходимо продифференцировать ответ и получить подынтегральную функцию. Другими словами интегральное исчисление решает задачу: по заданной производной или дифференциалу неизвестной функции требуется определить эту функцию. Отсюда можно сделать вывод, который мы запишем в виде определения (слайд 17)
Определение: совокупность всех первообразных функции f(x), определенных на некотором промежутке, называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается
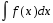
Из определения имеем:
 (1)
(1)
Неопределенный интеграл функции f(x), таким образом, представляет собой множество всех первообразных функций для f(x).
В равенстве (1)
-функцию f(x) называется подынтегральной функцией,
- выражение f(x)dx – подынтегральным выражением,
- переменную x – переменной интегрирования,
- слагаемое C - постоянной интегрирования.
Свойства неопределенного интеграла (слайды 18-19)
Опираясь на определение первообразной, легко доказать следующие свойства неопределенного интеграла
Производная от неопределенного интеграла равна подынтегральной функции, то есть если  = f(x), то
= f(x), то 
Дифференциал от неопределенного интеграла равен подынтегральному выражению
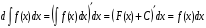
Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
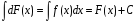
Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов
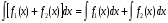
Постоянный множитель можно выносить за знак интеграла, то есть если a=const, то
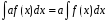
3. Таблица простейших интегралов (слайд 20)
1. 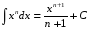 ,(n
,(n  -1)
-1)
2. 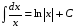
3. 
4. 
5. 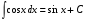
6. 
Интегралы, содержащиеся в этой таблице, принято называть табличными
Закрепление изученного материала
Рассмотреть примеры (слайды 21-22)
6.13(б, д), 6.14(в), 6.15(г), 6.16(д)
Домашнее задание: п. 6.1, № 6.13(е). 6.15(б)
Подведение итогов
Приложение:
- таблица первообразных
– основные свойства неопределенного интеграла
- основные формулы интегрирования
Таблица первообразных
| Функция | Первообразная |
| 
 | 
|
|  , k≠0 , k≠0
| 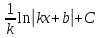
|
| 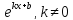
| 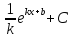
|
| sin(kx + b), k≠0 | |
| 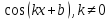
| 
|
| Функция | Первообразная |
| 
| 
|
|  , x 0, x , x 0, x
| 
|
| 
| 
|
| sin x | -cos x + C |
| 
| 
|
Основные свойства неопределенного интеграла:
Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:
.
Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
, .
Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:
;
Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:
.
Если и  – любая известная функция, имеющая непрерывную производную, то
– любая известная функция, имеющая непрерывную производную, то
.
Основные формулы интегрирования (таблица интегралов):
 ;
;
, (n );
);
 ;
;
 ;
;
 ;
;






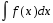
 (1)
(1) = f(x), то
= f(x), то 
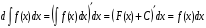
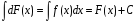
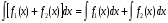
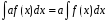
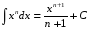 ,(n
,(n  -1)
-1) 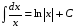


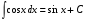




 , k≠0
, k≠0