Урок № 43 (19.12.2022) Геометрия, 10 класс
Тема урока: Решение задач по теме «Перпендикулярность прямых и плоскостей».
Цели:
закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
вырабатывать навыки применения теоретических знаний к решению типовых задач на перпендикулярность прямой и плоскости.
Тип урока: комбинированный
Ход урока
I.Организационный момент.
II. Сообщение темы и целей урока.
III. Актуализация опорных знаний и умений.
Теоретический опрос
1. Закончить предложение:
а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)
2. Дан параллелепипед
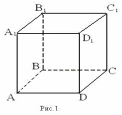
а) Назовите:
1) рёбра, перпендикулярные к плоскости (DCC1) (ответ: AD; A1D1; B1C1; BC)
2) плоскости, перпендикулярные ребру BB1 (ответ: (АВС); (A1B1C1))
б) Определите взаимное расположение:
1) прямой CC1 и плоскости (DСВ) (ответ: они перпендикулярны)
2) прямой D1C1 и плоскости (DCB) (ответ: они параллельны)
VI. Решение задач.
1. Решение задач по готовым чертежам (Устно)
№1
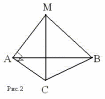
Дано: ∆ ABC - прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости. Ч.т.д.
№2
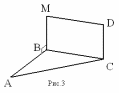
Дано: ВМDC - прямоугольник, M ∉ (ABC), MB ⊥ AB
доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВлежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВпо свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.
№3
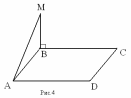
Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ иАВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.
№4
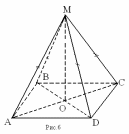
Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD - равнобедренный, т. к. ВМ = МD по условию, значит МО - медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.
(Устные ответы к каждой задаче требуется обосновывать, проговаривая всякий раз формулировки применяемых теорем)
2. Решение письменных задач №1.2
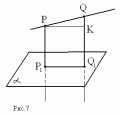
Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P1 и Q1. Найдите P1Q1, если PQ = 15 cм; PP1 = 21,5 cм; QQ1 = 33,5 cм.
Решение:
1) PP1 ⊥ α и QQ1 ⊥ α по условию ⇒ PP1 ∥ QQ1 (обосновать);
2) PP1 и QQ1 определяют некоторую плоскость β, α ⋂ β = P1Q1;
3) PP1Q1Q - трапеция с основаниями PP1 и QQ1, проведём PK ∥ P1Q1;
4) QK = 33,5 - 21,5 = 12 (см)
| P1Q1 = PK = | 
| = 9 см. |
Ответ: P1Q1 = 9 см.
№2.2
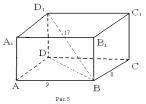
В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ = 9 см; ВС = 8 см; ВD = 17 см. Найдите площадь BDD1B1.
Решение:
1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;
| ВD = | 
| см; |
2) ∆ DD1B: ∠D1DB = 90°;
| DD1 = | 
| = 12 см; |
| 3) SBB1D1D = BD ∙ DD1 = | 
| см2. |
| Ответ: | 
| см2. |
№3.2
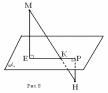
Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:
1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;
| 3) ∆ HPK: KP = | 
| = 3 см; |
4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),
| тогда ∆ MEK ∆ HPK по двум углам и | 
| ; т.е. | 
| ⇒ EK = | 
| = 9 см, |
РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.
Ответ: РЕ = 12 см.
3. Самостоятельная работа (направлена на проверку усвоения материала по данной теме)
| Вариант I | Вариант II |
| Через вершины А и В прямоугольника АВСD проведены параллельные прямые AA1 и BB1, не лежащие в плоскости прямоугольника. Известно, что AA1 ⊥ AB, AA1 ⊥ AD. Найдите B1B, если B1D = 25 см, AB = 12 см, AD = 16 см. | Через вершины А и В ромба АВСD проведены параллельные прямые AA1 и BB1, не лежащие в плоскости ромба. Известно, что BB1 ⊥ BC,BB1 ⊥ AB. Найдите A1A, если A1C = 13 см, BD = 16 см, AB = 10 см. |
| Решение: 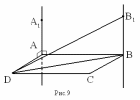
1) AA1 ⊥ AB, AA1 ⊥ AD, а AB ⋂ AD = A ⇒ AA1 ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. AA1 ∥ BB1, то BB1 ⊥ (ABC) ⇒ BB1 ⊥BD;
2) ∆ ABD: ∠BAD = 90°. По теореме Пифагора: | BD = | 
| = 20 см; | 3) ∆ B1BD – прямоугольный. По теореме Пифагора: | B1B = | 
| = 15 см. | Ответ: 15 см. | Решение: 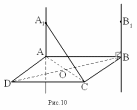 1) BB1 ⊥ AB, BB1 ⊥ BC, а AB ⋂ BC = B ⇒ BB1 ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB1 ∥ AA1, то AA1 ⊥ (ABC) ⇒AA1 ⊥ AC;
2) Используя свойство диагоналей ромба, имеем в ∆ AOB: ∠AOB = 90°, BO = ½ BD = 8 см. По теореме Пифагора: | AO = | 
| = 6 см, | AO = ½ AC ⇒ AC = 12 см;
3) ∆ A1AC – прямоугольный. По теореме Пифагора: | AA1 = | 
| = 5 см. | Ответ: 5 см. |
V. Подводятся итоги урока. Задание на дом: повторить теоретический материал по изученной теме, глава II, № 216 (подг.к к.р.)
Индивидуальное задание для более сильных учеников. (Вариант III)
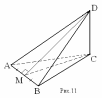
Дано: ∆ ABC; AB = AC = BC; CD ⊥ (ABC); AM = MB; DM = 15 дм; CD = 12 дм.
Найти: S∆ ADB
Решение:
1) Т.к. CD ⊥ (FDC) ⇒ CD ⊥ AC и CD ⊥ BC, т.е. ∆ ADC, ∆ BDC – прямоугольные;
2) ∆ ADC = ∆ BDC (по двум катетам) ⇒ AD = BD, т.е. ∆ ADB – равнобедренный и DM – медиана, а значит и высота; 3) DC ⊥ MC ⇒ MCD – прямоугольный,
| тогда MC = | 
| = 9; |
4) ∆ ABC – равносторонний, поэтому СМ – медиана и высота, т.е. ∆ MCB – прямоугольный, ∠B = 60°,
| sin ∠B = | 
| , тогда | 
| , |
а АВ = ВС (по условию).
5) S∆ ADB = ½ DM ∙ AB;
| S∆ ADB = ½ ∙ 15 ∙ | 
| . |
| Ответ: | 
|













































