Немченко Марина Германовна,
учитель математики МАОУ лицея №6 г. Тамбова
Система работы по подготовке старшеклассников к ЕГЭ по математике
Вместо предисловия
Экзамен по ЕГЭ по математике при правильной подготовке хорошо может сдать каждый. Формула успеха проста – высокая степень восприимчивости, мотивация и компетентный педагог. В любом случае натаскивание на варианты ЕГЭ необходимо, но его нужно сочетать с фундаментальной подготовкой, формируя системные знания и навыки.
Современный старшеклассник относится к ЕГЭ как к серьезному жизненному испытанию и связывает с его результатами свою возможность поступления в вуз. Поэтому на учителя выпускных классов ложится особая ответственность: с одной стороны, необходимо организовать качественную подготовку к предстоящему экзамену, а с другой стороны, не утратить личностного, творческого, мировоззренческого смысла преподаваемого предмета.
Трудности подготовки к ЕГЭ по математике обусловлены следующими объективно существующими противоречиями:
между осуществлением обязательного всеобщего среднего образования и реализацией принципа индивидуализации усвоения знаний;
между отсутствием у части школьников мотивации к изучению математики и необходимостью сдачи экзамена в формате ЕГЭ;
между возрастающей сложностью и насыщенностью школьной программы и неспособностью ученика освоить весь объем предлагаемых ему сведений.
Для разрешения сложившихся противоречий и эффективной подготовки учащихся к ЕГЭ необходимо решить следующие задачи.
Педагогические:
изучение индивидуальных особенностей каждого учащегося;
развитие его логического мышления;
формирование творческого, интеллектуального потенциала старшеклассника;
совершенствование у учащихся навыков самостоятельной работы.
Учебные:
ликвидация пробелов по основным темам курса математики;
отработка математических навыков в соответствии с требованием стандартов образования;
формирование навыка оформления экзаменационных работ;
выработка у школьников умения концентрироваться и продуктивно работать в условиях экзамена.
И тут более чем важна организация повторения при подготовке школьников к ЕГЭ как условие повышения качества образования.
Условия возникновения проблемы, становление опыта.
Осмысление проблемы качества образования в рамках модернизации Российского образования, становление системы подготовки школьников к ЕГЭ, необходимость развития личностных достижений учащихся привели к необходимости изучения и разработки данной проблемы.
Актуальность и перспективность опыта, его практическая значимость для повышения качества учебно-воспитательного процесса.
Актуальность обосновывается задачами модернизации образования и дальнейшим становлением системы подготовки школьников к ЕГЭ, направленной на повышение эффективности математического образования.
Теоретическая база опыта.
В основу решения проблемы повышения качества математического образования положены: теория Н.Я. Гальперина об управлении познавательной деятельностью ученика, психологический принцип Л.В. Выготского о ведущей роли обучения в развитии.
И здесь уместно вспомнить известных дидактов Выготского и Гальперина, говоривших о том, что:
знания усваиваются только в ходе собственной работы с этими знаниями;
нужно организовывать собственную самостоятельную работу каждого ученика с подлежащим усвоению этим конкретным учеником материалом;
нужно так организовать обучение, чтобы ученик понял, какой материал подлежит усвоению и каким образом с ним работать;
нужно так организовать собственную самостоятельную работу, чтобы каждый шаг ученика был подконтрольным учителю;
нужно перейти постепенно от пошагового контроля к самоконтролю.
Новизна опыта.
Разработка технологий, позволяющих целенаправленно организовать повторение учебного материала на всех этапах учебного процесса.
Разработка системы задач, направленных на углубление и расширение знаний учащихся по основным вопросам школьного курса математики.
Использование личностно-ориентированного подхода при организации повторения.
Технология опыта.
Обеспечение положительной мотивации учащихся на повторение ранее изученного материала;
выделение узловых вопросов программы, предназначенных для повторения;
использование различных видов повторения (вводное, текущее, поддерживающее, итоговое, систематизирующее, обобщающее);
использование схем, моделей, опорных конспектов, справочников.
Адресная направленность опыта.
Используя данный опыт, можно получить устойчивые положительные результаты, если:
будет обеспечена положительная мотивация учащихся на повторение ранее изученного материала;
в учебном процессе будет реализован личностно-ориентированный подход при обучении математике;
будет применяться система задач, которая способствует расширению, углублению, систематизации знаний учащихся;
содержание повторяемого материала и способы его подачи будут способствовать активизации мыслительной деятельности учащихся на уроках и в процессе самостоятельного приобретения знаний;
в процесс деятельности учащихся в арсенал приемов и методов мышления будут включены индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация.
Цели и задачи:
Подготовить всех учащихся к успешной сдаче ЕГЭ с хорошим качеством.
Для этого необходимо:
учителю обладать необходимыми компетенциями;
совершенствовать структуру и содержание учебного материала в ходе подготовки к ЕГЭ;
систематизировать повторение программного материала;
отработать тестовые технологии в ходе работы с контрольно-измерительными материалами через личностно-ориентированный подход.
Моя цель заключается в том, чтобы:
адаптировать содержания образования к современным требованиям ЕГЭ;
развивать творческие способности и самостоятельную активность учащихся;
сочетать лекции, самостоятельную работу, поиск информации в сети, практикумы с широкой организацией диалогического общения, консультаций;
вести систематический контроль обученности учащихся;
вести мониторинг выполнения типовых заданий.
Ориентируясь на данные компоненты, актуальными вопросами в подготовке к ЕГЭ являются следующие:
Подготовка к сдаче ЕГЭ по математике должна идти через приобретение и освоение конкретных математических знаний. Только это обеспечит выпускнику успешную сдачу экзамена.
В своей работе применяю следующие принципы подготовки к ЕГЭ.
Первый принцип – тематический. Эффективнее выстраивать такую подготовку, соблюдая принцип от простых типовых заданий к сложным.
Второй принцип – логический. На этапе освоения знаний необходимо подбирать материал в виде логически взаимосвязанной системы, где из одного следует другое. На следующих занятиях полученные знания способствуют пониманию нового материала.
Третий принцип – тренировочный. На консультациях учащимся предлагаются тренировочные тесты, выполняя которые дети могут оценить степень подготовленности к экзаменам.
Четвёртый принцип – индивидуальный. На консультациях ученик может не только выполнить тест, но и получить ответы на вопросы, которые вызвали затруднение.
Пятый принцип – временной. Все тренировочные тесты следует проводить с ограничением времени, чтобы учащиеся могли контролировать себя - за какое время сколько заданий они успевают решить.
Шестой принцип – контролирующий. Максимализация нагрузки по содержанию и по времени для всех учащихся одинакова. Это необходимо, поскольку тест по своему назначению ставит всех в равные условия и предполагает объективный контроль результатов.
Следуя этим принципам, формирую у учеников навыки самообразования, критического мышления, самостоятельной работы, самоорганизации и самоконтроля.
Моя цель состоит в том, чтобы помочь каждому школьнику научиться быстро решать задачи, оформлять их чётко и компактно. Развиваю способность мыслить свободно, без страха, творчески. Стараюсь давать возможность каждому школьнику расти настолько, насколько он способен.
Устный счет – один из важных приемов при подготовке учащихся к ЕГЭ по математике
Устные упражнения как этап урока имеют свои задачи:
воспроизводство и корректировка знаний, умений и навыков учащихся, необходимых для их самостоятельной деятельности на уроке или осознанного восприятия объяснения учителя;
контроль состояния знаний учащихся;
автоматизация навыков простейших вычислений и преобразований.
В связи с введением обязательного ЕГЭ и ГИА по математике возникает необходимость научить учащихся старших классов решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных вычислений и вычислений вообще, так как на экзамене не разрешается использовать калькулятор и таблицы. Заметим, что многие вычислительные операции, которые мы имеем обыкновение записывать в ходе подробного решения задачи, в рамках теста совершенно не требуют этого. Можно научить учащихся выполнять простейшие (и не очень) преобразования устно. Конечно, для этого потребуется организовать отработку такого навыка до автоматизма.

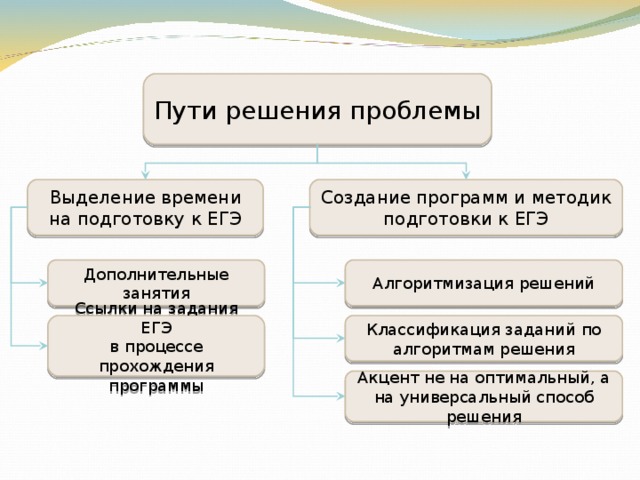
Классификация заданий по алгоритмам решения (слайды 18, 19).

Универсальный способ решения - способ, с помощью которого можно решить как можно большее количество задач.
Метод координат
Преимущества метода:
80% заданий данной группы можно решить с помощью этого метода;
у учащихся появляется возможность избежать ошибки, связанной с построением;
метод имеет очень отлаженный алгоритм решения: решение всех задач сводится к одной формуле.
Литература для подготовки к ЕГЭ 2012, ЕГЭ и ГИА 2013 (Слайды 23, 24).
Применение ИКТ на уроках математики при подготовке к ЕГЭ
программы – тренажеры для отработки теоретических знаний и развития практических умений и навыков (тренажер по математике издательства «Кирилл и Мефодий» для 11 классов, тренажеры можно найти у своих коллег на сайте «Первое сентября»);
ресурсы сети: http://alexlarin.net/ege.html, http://www1.ege.edu.ru/gia, http://www.school-tests.ru/online-ege-math.html;
открытый банк заданий ЕГЭ по математике http://mathege.ru;
тесты сайта «РЕШУЕГЭ» http://reshuege.ru;
http://statgrad.mioo.ru/sg11_12/grafik.htm , Статград;
http://ucheba.pro/ , задания ЕГЭ- 2013 по математике – подробные решения заданий С.
Результаты фиксируются в журнале в системе NetSchool.
Комплексный подход к деятельности по подготовке учащихся к ЕГЭ
Администрация нашего лицея пришла к выводу о том, что только комплексный подход к деятельности по подготовке учащихся к ЕГЭ и ГИА способствует повышению эффективности и качества результатов экзамена в тестовой форме. Под комплексным подходом мы понимаем целенаправленное сотрудничество администрации, учителей-предметников, учащихся и их родителей.
В информационной деятельности нашего образовательного учреждения по подготовке к ЕГЭ и ГИА мы выделяем три направления: информационная работа с педагогами, с учащимися, с родителями.
Мониторинг качества образования.
Мониторинг качества должен быть системным и комплексным. Он должен включать следующие параметры: контроль текущих оценок по предметам, выбираемыми учащимися в форме ЕГЭ и ГИА, оценок по контрольным работам, оценок по самостоятельным работам, результаты пробного внутрилицейского ЕГЭ и ГИА. Учитель анализирует их, выносит на обсуждение на административные и производственные совещания, доводит до сведения родителей. Мониторинг обеспечивает возможность прогнозирования оценок на выпускном ЕГЭ и ГИА.
Психологическая подготовка к ЕГЭ.
Психологическая подготовка учащихся может заключается в следующем: отработка стратегии и тактики поведения в период подготовки к экзамену; обучение навыкам саморегуляции, самоконтроля, повышение уверенности в себе, в своих силах.
Методы проведения занятий по психологической подготовке учащихся разнообразны: групповая дискуссия, игровые методы, медитативные техники, анкетирование, мини-лекции, творческая работа, устные или письменные размышления по предложенной тематике. Содержание занятий должно ориентироваться на следующие вопросы: как подготовиться к экзаменам, поведение на экзамене, способы снятия нервно-психического напряжения, как противостоять стрессу.
Работа с учащимися проводится по желанию учащихся – со всем классом или выборочно.
СЛОЖИВШАЯСЯ СИСТЕМА ПОДГОТОВКИ К ЕГЭ ДАЕТ СТАБИЛЬНЫЕ РЕЗУЛЬТАТЫ.
Результаты ЕГЭ моих выпускников.
Все годы: обученность – 100%, качество – 100%
| Год | Средний балл по Тамбову | Средний балл моих выпускников | Самый высокий результат |
|
|
| 2009 | 50,9 | 75,6 | 86 |
| 2011 | 53,6 | 76,4 | 89 |
| 2012 | 46,2 | 67,7 | 90 |
Результаты моих учеников.
| Год | Городские олимпиады | Областные олимпиады |
|
|
| 2009-2010 | Призеры: Федосеева Любовь (10А), Малыкова Наталья (10А), Горелкина Анастасия (10А), Танвель Михаил (10А), Ольшевская Кристина (10А) | Призеры: Горелкина Анастасия (10А) |
| 2010-2011 | Призеры: Горелкина Анастасия (11А), Федосеева Любовь (11А) | Призеры: Горелкина Анастасия (11А), Федосеева Любовь (11А) |
| 2011-2012 | Победитель: Моисеева Вера (7А) Призеры: Круглова Ксения (7А), Миронова Татьяна (7А), Косогоров Никита (7А), Панафидина Софья (11А) | Призеры: Панафидина Софья (11А) |