Урок № 57-58 10-а (19.12.2017)
Тема: Перпендикулярність прямих у просторі.
Мета: сформувати в учнів поняття про перпендикулярні прямі у просторі; взаємозв’язок між перпендикулярністю та паралельністю прямих у просторі; сформувати вміння застосовувати теоретичні знання при розв’язуванні задач.
Тип: засвоєння нових знань та вмінь.
Хід уроку І. Організаційний етап. ІІ.Аналіз контрольної роботи. IIІ. Перевірка домашнього завдання.
В кінці уроку збираються учнівські зошити для перевірки їх ведення та виконання домашнього завдання.
4.Актуалізація.
Запитання до класу.
1.Які прямі називаються перпендикулярними на площині?
2.скільки існує в площині прямих, перпендикулярних до даної, таких, що проходять через дану точку.
3.Сформулюйте ознаку паралельності прямих.
4.Що називають паралелограмом?
5.Сформулюйте властивість сторін паралелограма?
6.Сфолрмулюйте ознаки рівності трикутників.
5.Формулювання мети та завдань уроку.
6.Формування знань.
План.
1.Означення перпендикулярних прямих.
2.Теорема про властивості прямих, відповідно паралельних перпендикулярним прямим.
3.Розвязування задач.
Означення перпендикулярних прямих у просторі
Поряд із відношенням паралельності в геометрії важливе значення має відношення перпендикулярності. У планіметрії ми говорили про перпендикулярність прямих. Перпендикулярними прямими на площині називаються прямі, які перетинаються під прямим кутом.
У стереометрії розглядають три випадки перпендикулярності: перпендикулярність прямих, перпендикулярність прямої і площини, перпендикулярність площин. На наступних уроках ми займемося послідовним вивченням цих трьох відношень. Почнемо з випадку перпендикулярності прямих у просторі.
Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Розв'язування задач
1. Назвіть в оточенні моделі прямих, які перпендикулярні між собою.
2. Дано зображення куба АBСDA1B1C1D1. Укажіть ребра куба, які перпендикулярні до прямої АА1.
Теорема про прямі, що перетинаються і паралельні двом перпендикулярним прямим
Питання до класу: що можна стверджувати про взаємне розташування прямих а1 і b1, які перетинаються і а1 || а, b1 || b, а  b? Учні висувають гіпотезу, що a1
b? Учні висувають гіпотезу, що a1  b1. Для ілюстрації цього твердження використовується каркасна модель куба або прямокутного паралелепіпеда.
b1. Для ілюстрації цього твердження використовується каркасна модель куба або прямокутного паралелепіпеда.
Далі формулюємо теорему:
Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони теж перпендикулярні.
Доведення цієї теореми проводить учитель. Подаємо запис доведення теореми, який рекомендується зробити на дошці і в зошитах учнів.
Дано: a b, а
b, а α, b
α, b α; а1||а, b1||b, а1
α; а1||а, b1||b, а1 α1, b1
α1, b1 α1, а1 і b, перетинаються (рис. 131).
α1, а1 і b, перетинаються (рис. 131).
Довести: а1  b1
b1
Доведення
| Номер п/п
| Твердження
| Аргумент
|
| 1
| а і b лежать в α , а1 і b1 лежать в α1
| Сз
|
| 2
| а || а1
| Теорема 2.4
|
| 3
| Нехай точка С — точка перетину а і b, точка С1 — точка перетину а1 і b1 | Означення
|
| 4
| AA1 || СС1, ВВ1 || CC1
| Теорема 2.1
|
| 5
| A1A2 || BB1
| Теорема 2.2
|
| 6
| CAA1C1 і CBB1C1 — паралелограми, отже, AC = А1С1, BC = B1C1
| AC||A1C1;AA1 || CC1, СВ || С1В1, ВВ1 || СС1 |
| 7
| АВB1А1 — паралелограм, отже, АВ = А1B1,
| АВ||А1B1, AA1 || ВВ1
|
| 8
| ΔАВС =ΔА1В1С1, отже, A1C1B1= ACB = 90°, тоді а1  b1 b1
| Третя ознака рівності трикутників |


Розв'язування задач
1. SABC — тетраедр; ABC = 90°; точки К, L, М — середини ребер SB, SA, SC відповідно (рис. 132). Знайти MKL.
2. Дано зображення куба ABCDA1B1C1D1 (рис. 133). Точки М, N, Р, К — точки перетину діагоналей граней АВВ1А1, CDD1C1, А1B1С1D1 і ABCD відповідно. Довести, що MN  РК .
РК .
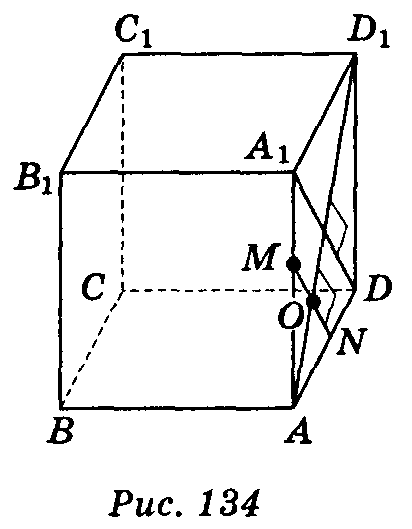
3. Дано куб ABCDA1B1C1D1. Через точку М, що належить ребру АА1 в грані AA1DD1, проведіть пряму MN так, щоб MOD1 = 90° , де точка О — точка перетину прямих MN і AD1.
Розв'язання
Проведемо в квадраті A1ADD1 діагоналі AD1 і A1D (AD1 A1D) (рис. 134). Через точку М ребра АА1 в грані АDD1А1 проведемо пряму MN || А1D . За теоремою 3.1 MN
A1D) (рис. 134). Через точку М ребра АА1 в грані АDD1А1 проведемо пряму MN || А1D . За теоремою 3.1 MN  AD1, оскільки A1OD1 = 90° .
AD1, оскільки A1OD1 = 90° .
4. Дано куб ABCDA1B1C1D1. Через точку О грані А1АDD1 проведіть прямі ОМ і ON так, щоб ОМ || ВС , ON || СС1. Доведіть, що MON = 90° .
5. Через точку О перетину діагоналей куба ABCDA1B1C1D1 проведіть площину α, паралельну основі А1B1С1D1 куба. Доведіть, що 1 і BВ1 з площиною α.
6.Промені ОА, 0В, ОС попарно перпендикулярні. Знайдіть периметр і площу трикутника АВС, якщо ОА = 0В = ОС = а .
(Відповідь. 3 ,
, 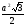 .)
.)
7. А, В, С — точки на попарно перпендикулярних променях ОА, ОВ, ОС. Знайдіть кути трикутника АВС, якщо ОА = 0В = ОС .
(Відповідь. = = = 60° .)
8.Математичний диктант.
У прямокутному паралелепіпеді:
варіант 1 — АВ = 1 см, AD = 2 см, ВС = 3 см;
варіант 2 — АВ = 1 см, AD = 3 см, ВС = 2 см (рис. 136).
Знайдіть:
а) діагональ BD грані прямокутного паралелепіпеда; (2 бали)
б) довжину ребра АС; (2 бали)
в) діагональ DC грані куба; (2 бали)
г) прямі, які перпендикулярні до прямої АС; (2 бали)
д) величину кута BDA; (2 бали)
е) величину кута СВА. (2 бали)
Відповідь. Варіант 1. а)  см; б) 2
см; б) 2 см; в) 2
см; в) 2 см; г) AD, AB, CF, CM; д) arctg
см; г) AD, AB, CF, CM; д) arctg  ; e) arccos
; e) arccos  .
.
Варіант 2.а) см; б)
см; б) см; в) 2
см; в) 2 см; г) AD, AB, CF, CM; д) arctg
см; г) AD, AB, CF, CM; д) arctg ; е) arccos
; е) arccos .
.
9.Дано пряму а і точку А, яка не належить прямій а. Провести пряму, яка проходить через точку А і перпендикулярна до прямої а. Скільки прямих, перпендикулярних до прямої а, можна провести через точку А, яка не лежить на прямій?
10. Дано зображення куба ABCDA1B1C1D1. Укажіть пряму, яка перпендикулярна до прямої АА1 і проходить через точку С. (Відповідь. АС.)
11. Дано пряму а і точку А, яка лежить на прямій а. Провести пряму, яка проходить через точку А і перпендикулярна до прямої а. Скільки прямих, перпендикулярних до прямої а, можна провести через точку А, яка лежить на прямій а?
12. Дано зображення куба ABCDA1B1C1D1. Укажіть прямі, які перпендикулярні до прямої АА1 і проходять через точку А. (Відповідь. AB, AC, AD.)
7.Підведення підсумків.
8. Домашнє завдання. Параграф 12, № 430,434.







 b? Учні висувають гіпотезу, що a1
b? Учні висувають гіпотезу, що a1 
 α, b
α, b


 ,
, 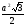 .)
.)
 см; б) 2
см; б) 2 см; г) AD, AB, CF, CM; д) arctg
см; г) AD, AB, CF, CM; д) arctg  ; e) arccos
; e) arccos  .
.  см; б)
см; б)









