ОГАПОУ «Белгородский индустриальный колледж»
Лекция № 5
Учебные группы: 21 ПКС, 22 ПКС
Тема занятия: Тавтология и противоречие. Классификация формул алгебры логики. Законы логики.
Вид занятия: комбинированное
Цель занятия (дидактическая): изучить тавтологию и противоречие. Классификация формул алгебры логики. Законы логики.
Определение. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Обозначение. A≡B.
Пример.
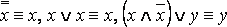 .
.
Определение. Формула A называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных (напр., 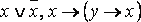 ).
).
Определение. Формула A называется тождественно ложной (противоречием), если она принимает значение 0 при всех значениях входящих в нее переменных (напр., 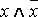 ).
).
Утверждение. Отношение равносильности рефлексивно, симметрично, транзитивно.
Связь между понятиями равносильности и эквивалентности: если формулы A и B равносильны, то формула A↔B тавтология, и обратно, если формула A↔B тавтология, то формулы A и B равносильны.
Равносильности алгебры логики можно разбить на 3 группы:
1. Основные равносильности.
· 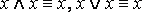 – законы идемпотентности;
– законы идемпотентности;
· 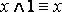 ;
;
· 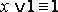 ;
;
· 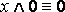 ;
;
· 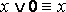 ;
;
· 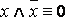 – закон противоречия;
– закон противоречия;
· 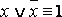 – закон исключенного третьего;
– закон исключенного третьего;
· 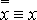 – закон снятия двойного отрицания;
– закон снятия двойного отрицания;
· 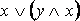
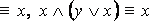 – законы поглощения.
– законы поглощения.
2. Равносильности, выражающие одни логические операции через другие:
· 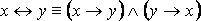 ;
;
· 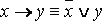 ;
;
· 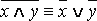 ;
;
· 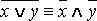 ;
;
· 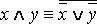 ;
;
· 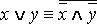 .
.
Замечание. Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание, или дизъюнкцию и отрицание. Дальнейшее исключение операций невозможно. Например, если использовать только конъюнкцию, то уже такая простая формула, как 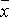 не может быть выражена с помощью операции конъюнкции.
не может быть выражена с помощью операции конъюнкции.
Существуют операции, с помощью которых может быть выражена любая из 5 логических операций:
1) Связка Шеффера – дизъюнкция отрицаний.
Обозначение. x|y≡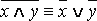 («x не совместно с y»).
(«x не совместно с y»).
Логические значения связки Шеффера описываются следующей таблицей истинности:
| x | y | x|y |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Имеют место следующие равносильности: а) 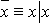 ; б)
; б) 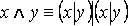 .
.
2) Стрелка Пирса – конъюнкция отрицаний.
Обозначение. x↓y≡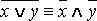 («ни x, ни y»).
(«ни x, ни y»).
Логические значения стрелки Пирса описываются следующей таблицей истинности:
| x | y | x↓y |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
3. Равносильности, выражающие основные законы алгебры логики:
· 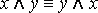 – коммутативность конъюнкции;
– коммутативность конъюнкции;
·  – коммутативность дизъюнкции;
– коммутативность дизъюнкции;
·  – ассоциативность конъюнкции;
– ассоциативность конъюнкции;
·  – ассоциативность дизъюнкции;
– ассоциативность дизъюнкции;
·  – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции;
·  – дистрибутивность дизъюнкции относительно конъюнкции.
– дистрибутивность дизъюнкции относительно конъюнкции.
Замечание. Равносильности группы 3 показывают, что над формулами алгебры логики можно проводить те же преобразования, что и в алгебре чисел.
3. Законы логики и правила преобразования логических выражений
Закон двойного отрицания (двойное отрицание исключает отрицание):
А =  .
.
Переместительный (коммутативный) закон:
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
Сочетательный (ассоциативный) закон:
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
Распределительный (дистрибутивный) закон:
Закон определяет правило выноса общего высказывания за скобку.
Закон общей инверсии (законы де Моргана):
Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):
Закон означает отсутствие показателей степени.
Законы исключения констант:
для логического сложения: А 1 = 1, А 0 = A;
для логического умножения: A ˄ 1 = A, A ˄ 0 = 0.
Закон противоречия:
A ˄  = 0.
= 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
Закон исключения третьего:
A  = 1.
= 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
Закон поглощения:
Формулы склеивания:
Формулы с импликацией и эквивалентностью:
Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие - основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.
Упрощение формул.
Пример 1. Упростить формулу (А В) ˄ (А С).
Решение:
Раскроем скобки: (А В) ˄ (А С) = A ˄ A A ˄ C B ˄ A B ˄ C;
По закону идемпотентности A ˄ A =A, следовательно,
A ˄ A A ˄ C B ˄ A B ˄ C = A A ˄ C B ˄ A B ˄ C;
В высказываниях А и А ˄ C вынесем за скобки А и используя свойство А + 1= 1, получим
A A ˄ C B ˄ A B ˄ C = A ˄ (1 C) B ˄ A B ˄ C = A B ˄ A B ˄ C;
Аналогично предыдущему пункту вынесем за скобки высказывание А.
A B ˄ A B ˄ C = A ˄ (1 B) B ˄ C = A B ˄ C.
Таким образом, мы доказали закон дистрибутивности.
Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.
Пример 2. Упростить выражения так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.
Решение:
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) 
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);
2) 
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);
3) 
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания);
4)
(вводится вспомогательный логический сомножитель ( ); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
5) 
(сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
6) 
(выносятся за скобки общие множители; применяется правило операций с константами);
7)
(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания);
8)
(общий множитель x выносится за скобки, комбинируются слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции  применяется правило операции переменной с её инверсией);
применяется правило операции переменной с её инверсией);
9)
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);
10)
(используются правило де Моргана, закон двойного отрицания и закон поглощения).
4
















