Перспектива здания

Перспектива здания

Выполнила:

Ученица 10 класса «А»

Масякина Анастасия Романовна

Научный руководитель:

Сухненко Ирина Александровна

учитель математики

Введение

Одними из самых актуальных сфер деятельности в настоящее время являются строительство и архитектура. Огромное количество школьников стараются стать студентами в этих сферах. И это не случайно, ведь развивается наука, строятся здания, образуется все большее количество компаний и требуется больше квалифицированных специалистов. Архитекторы , инструкторы, инженеры работают в команде, в результате получая практичные решения многих объектов.

Актуальность исследования

Огромную важность приобретает вопрос проектирования зданий, строений, сооружений. Эти проекты чрезвычайно многообразны: различные многоквартирные дома, детские сады, школы, семейные коттеджи, стадионы, скверы и пр. Не менее важной проблемой является изображение проектируемого объекта в перспективе для его наглядности.

Цели и задачи исследования

Данная работа имеет целью рассмотреть способы проецирования и виды перспектив в архитектуре, исследовать способы их построения, раскрыть данную тему, построить перспективу выбранного здания после изучения и разбора основных понятий и способа построения.

Центральное проецирование

Пример 2. Задается плоскость проекций П 1 , центр проецирования S и точки А , В и С , где С , А и S лежат на одной прямой и все точки не лежат в плоскости П 1 .(Рис.2)

Пример 1. Задается плоскость проекций П о   , центр проецирования S и точка А , не лежащая в плоскости.(Рис.1)

Рисунок 1.

Рисунок 2.

Проведя из S через А прямую до пересечения с плоскостью П о   , получим А о – центральную проекцию   точки А .

Проведя из S через А, В и С прямые до пересечения с плоскостью П 1   , получим А 1 =С 1 и В 1 – центральные проекции   точек, где.

При заданных плоскости проекций и центре проецирования одна точка в пространстве имеет одну центральную проекцию, но если есть проекция точки, S и плоскость, то точку в пространстве найти нельзя.

Каждая точка на плоскости проекций может быть проекцией бесконечного множества точек.

Перспектива

Перспекти́ва (фр.  perspective  от лат.   perspicere – смотреть сквозь ) – это изображение, полученное центральным проецированием предмета на какую-либо поверхность. Виды перспективы в архитектуре:

• Прямая линейная перспектива.
• Обратная линейная перспектива.
• Фронтальная перспектива.
• Угловая перспектива.
• Аксонометрия (делится на изометрию, диметрию и триметрию).
• Билатеральная (или параллельная) перспектива.

Существуют так же: панорамная, сферическая, воздушная(или тональная), перцептивная, плафонная, наблюдательная перспективы и аспектива.

Перспективный масштаб

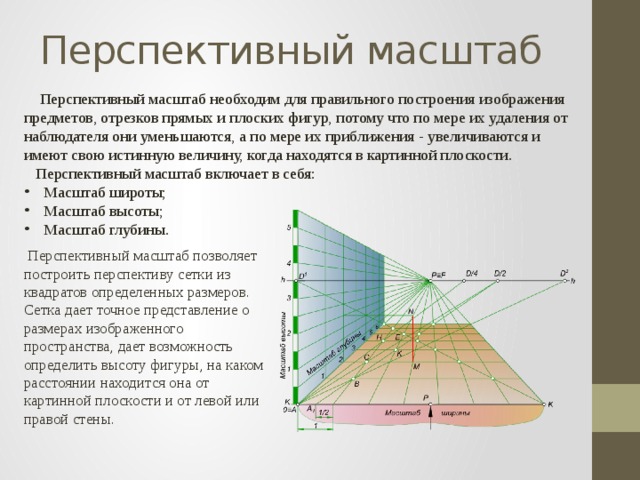
Перспективный масштаб необходим для правильного построения изображения предметов, отрезков прямых и плоских фигур, потому что по мере их удаления от наблюдателя они уменьшаются, а по мере их приближения - увеличиваются и имеют свою истинную величину, когда находятся в картинной плоскости.

Перспективный масштаб включает в себя:

• Масштаб широты;
• Масштаб высоты;
• Масштаб глубины.

Перспективный масштаб позволяет построить перспективу сетки из квадратов определенных размеров. Сетка дает точное представление о размерах изображенного пространства, дает возможность определить высоту фигуры, на каком расстоянии находится она от картинной плоскости и от левой или правой стены.

Точка зрения перспективы

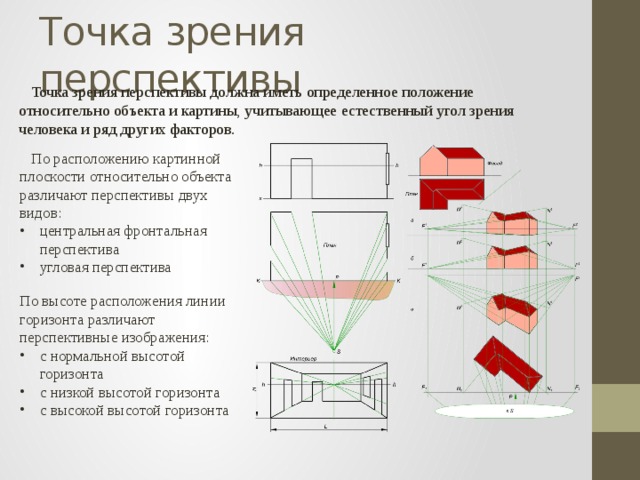
Точка зрения перспективы должна иметь определенное положение относительно объекта и картины, учитывающее естественный угол зрения человека и ряд других факторов.

По расположению картинной плоскости относительно объекта различают перспективы двух видов:

• центральная фронтальная перспектива
• угловая перспектива

По высоте расположения линии горизонта различают перспективные изображения:

• с нормальной высотой горизонта
• с низкой высотой горизонта
• с высокой высотой горизонта

Метод построения перспективы многоугольника в предметной плоскости

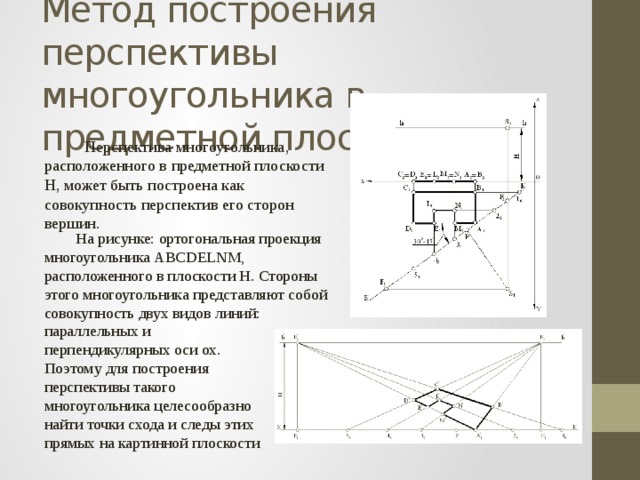
Перспектива многоугольника, расположенного в предметной плоскости H, может быть построена как совокупность перспектив его сторон вершин.

На рисунке: ортогональная проекция многоугольника АВСDELNM, расположенного в плоскости Н. Стороны этого многоугольника представляют собой совокупность двух видов линий:

параллельных и перпендикулярных оси ох. Поэтому для построения перспективы такого многоугольника целесообразно найти точки схода и следы этих прямых на картинной плоскости

Метод построения перспективы здания

Перспектива здания (сооружения) складывается из перспективы множества точек, каждая из которых строится как след луча зрения на картинной плоскости. Существует несколько способов построения перспективы, но для построения перспективы здания чаще используют способ архитекторов.

Впервые этот способ был предложен в 1693 году итальянским художником и архитектором Андреа дель Поццо. Позднее данный способ был назван «метод Андреа Поццо». В настоящее время построение перспективного изображения объектов по плану и фасаду, основанное на этом методе, называют способом архитекторов.

Построение в перспективе архитектурного объекта состоит из нескольких этапов и выполняется в определенной последовательности.

Построение перспективного изображения здания

Заключение

Подводя итог моей работы, с уверенностью могу заявить, что, работая над проектом, я успешно справилась с реализацией поставленных целей. Для их достижения я изучила литературу по данному вопросу, в которой разобрала различные виды проецирования и перспектив, рассмотрела понятия перспективного масштаба и точки зрения перспективы, алгоритм построения перспективы многоугольника, лежащего в предметной плоскости, и только после этого перешла непосредственно к перспективе здания. Подробно изучив и изложив в моей работе все основные необходимые моменты, требующиеся для построения перспективы здания, я также попробовала сделать ее самостоятельно, что вышло довольно успешно.

Знания, полученные в ходе проекта, позволили мне сильнее развить мои творческие способности и расширить программу, получаемую на уроках математики.

Спасибо за внимание!!!