
Первообразная и интеграл
Преподаватель ГБПОУ СО «Свердловский областной педагогический колледж»
Перминова Е.В.

Первообразная

Определение первообразной
y = F(x) называют первообразной для y = f(x) на промежутке X, если при x ∈ X
F'(x) = f(x)
функция y = F(х) (первообразная)
y = f(х)
производная
Операция
интегри-
рования
Операция
дифферен-цирования

Доказать, что функция
является первообразной для функции
Решение:

Доказать, что функция
является первообразной для функции
Решение:

Запомните:
Первообразная – это родитель производной:
F'(x) = f(x)

Первообразная
Первообразная
Элементарные функции
Элементарные функции
f(x)
f(x)
F(x)
Сложные функции
Сложные функции
F(x)
f(kx+b)
f(kx+b)
F'(x) = f(x)

Три правила нахождения первообразных
Если функции у=f(x) и у=g(x) имеют на промежутке
первообразные соответственно у=F(x) и у=G(x) , то
Функция
Первообразная
у = f(x) + g(x)
у = F(x) + G(x)
у =k f(x)
у =k F(x)

Задача.
Для функции y=f(x) найдите первообразные:
а)
б)
а)
а)
в)
б)
г)
б)
+C
в)
д)
е)
г)
в )
д)
е)
г)
д)
е)

Самостоятельно
Для функции y=f(x) найдите первообразные:
а)
а)
а)
б)
б)
б)
+C
в)
в)
в)
г)
г)
г)
д)
д)
д)
е)
е)
е)

Основное свойство первообразных
Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также является первообразной функции f(x).
Геометрическая интерпретация
y
- Графики всех первообразных данной функции f(x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси y.
x

Неопределенный интеграл.
Способы вычисления
11

Интегральное исчисление появилось во времена античного периода развития математической науки и началось с метода исчерпывания, который разработан математиками Древней Греции, и представлял собой набор правил, разработанных Евдоксом Книдским . По этим правилам вычисляли площади и объёмы
Евдокс Книдский
ок. 408 — ок. 355 год до н. э.

Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa).
Лейбниц Готфрид Вильгельм (1646-1716)

Ньютон и Лейбниц
открыли независимо друг от друга факт,
известный под
названием формулы
Ньютона – Лейбница.
Готфрид Вильгельм Лейбниц (1646—1716)
Исаак Ньютон
(1643 – 1727)

Работы Коши и Вейерштрасса
подвели итог многовековому развитию интегрального исчисления.
Огюстен Луи Коши (1789 – 1857)
Карл Теодор Вильгельм Вейерштрасс (1815 1897 )

В развитии интегрального исчисления приняли участие русские математики :
В.Я. Буняковский
(1804 – 1889)
П.Л. Чебышев
(1821 – 1894)
М.В. Остроградский
(1801 – 1862)

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b) называют любую ее первообразную функцию.
Где С – произвольная постоянная (const).

Установить соответствие. Найти такой общий вид первообразной, которая соответствует заданной функции.
1. F(x) =Сх+С
2. F(x) =
3. F(x) =
4. F(x) = sin x+С
5. F(x) = сtg x+С
6. F(x) = - cos x+С
1.f(x) = х n
2.f(x) = C
3.f(x)=sinx
tg x+С
4. f(x) =
5.f(x) =cosx
6.f(x)=

Свойства интеграла

Свойства интеграла

Основные методы интегрирования
2.Сведение к табличному преобразованием подынтегрального выражения в сумму или разность.
3.Интегрирование с помощью замены переменной (подстановкой).
4.Интегрирование по частям .

Верно ли что:
а) в)
б)
г)
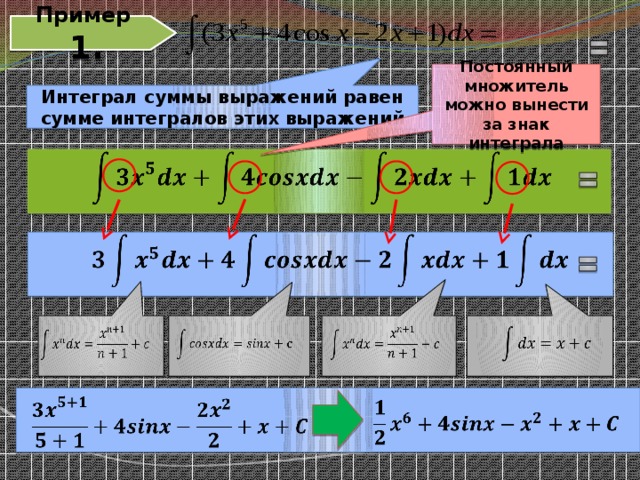
Пример 1.
Постоянный множитель можно вынести за знак интеграла
Интеграл суммы выражений равен сумме интегралов этих выражений
11

Пример 2.
Проверить
решение
Записать решение:

Пример 3.
Проверить решение
Записать решение:
11

Пример 4 .
Проверить решение
Записать решение:
Введем новую переменную и
выразим дифференциалы:

Проверить решение
Пример 5.
Записать решение:

проинтегрируйте функций :
1) =
2) =
3)
4)
5)
6)
5 х ² + C
х³ + C
-cos х +5х+ C
5sin x + C
2 х³ + C
3 x - х²+ C

Cамостоятельная работа
Найти неопределенный интеграл
Проверить решение
Уровень «В» (на «4»)
Уровень «А» (на «3»)
Уровень «С» (на «5»)

Задание Установить соответствие. Найти такой общий вид первообразной, которая соответствует заданной функции.

.

Определенный интеграл
![Определенный интеграл (Формула Ньютона - Лейбница) Для непрерывной функции на отрезке [a;b] где F(x) – первообразная функции f(x).](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img33.jpg)
Определенный интеграл (Формула Ньютона - Лейбница)
- Для непрерывной функции на отрезке [a;b]
где F(x) – первообразная функции f(x).

Основные свойства определенного интеграла

Основные свойства определенного интеграла

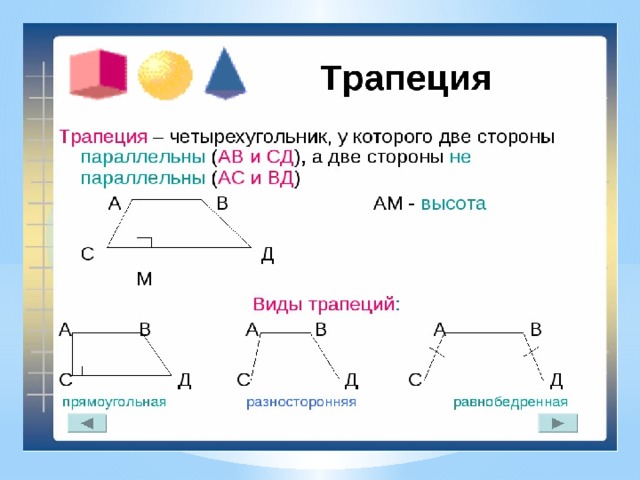
Площадь криволинейной трапеции

1. На клетчатой бумаге с клетками размером 1 см × 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
Ответ:26

2. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.
Ответ:9

3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.
Ответ:14

4. На клетчатой бумаге с клетками размером 1 см × 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Ответ:12,5

5. На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите .
Ответ:8

6. Найдите площадь трапеции, изображенной на рисунке.
Ответ:10

7. Найдите площадь закрашенной фигуры на координатной плоскости.
Ответ:32

7.Как найти площадь рыбки?

![Площадь криволинейной трапеции В декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a и графиком непрерывной неотрицательной на отрезке [a;b] функции y=f(x) , называется криволинейной трапецией](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img47.jpg)
Площадь криволинейной трапеции
В декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a и графиком непрерывной неотрицательной на отрезке [a;b] функции y=f(x) , называется криволинейной трапецией
У=0,5х+1
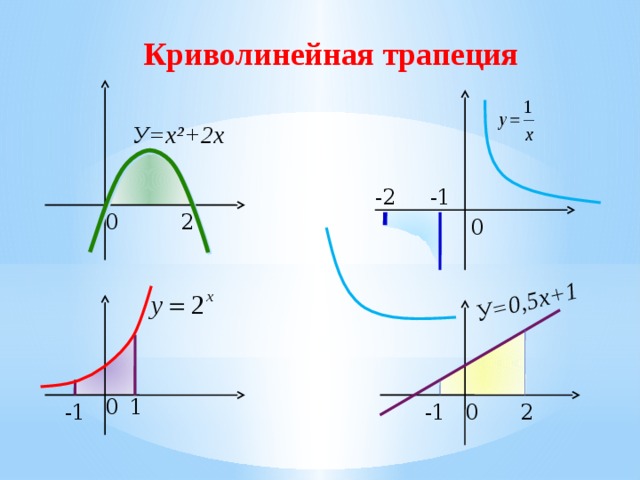
Криволинейная трапеция
У=х²+2х
-1
-2
0
2
0
1
0
2
-1
-1
0

Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет?
Заполнить таблицу
№ 1
№ 2
Да/нет
№ 3
№ 4
№ 5
№ 6
Задание для заполнения таблицы на следующем слайде

2
3
1
Не верно
верно
верно
у
у
у
y = f(x)
y = f(x)
3
y = f(x)
У=1
0
х
0
х
0
х
6
4
5
y = f(x)
у
у
у
y = f(x)
y = f(x)
У=3
Для проверки триггер – нажать на кнопку с № ответа (верно/неверно)
0
х
0
х
0
х
Не верно
верно
Не верно
51

Примеры
y
y
Y=f(x)
Y=f(x)
0
a
b
0
a
b
x
x
y
y
Y=f(x)
b
a
0
x
b
a
0
x
Y=f(x)
52

Вычислите площадь криволинейной трапеции 2-мя способами
1) Используя формулу площади
трапеции из геометрии, получим:
у
5
3
2) Найдите F(x) и вычислите
S по формуле S=F(b)-F(a)
1
х
3
О
1

x = 2
№ 999(1). Изобразить криволинейную трапецию, ограниченную графиком функции y = (x- 1 ) 2 , осью Ox и прямой x =2.
Анимация по щелчкам –построение графика – сдвиг оси ОУ на 1 влево
53
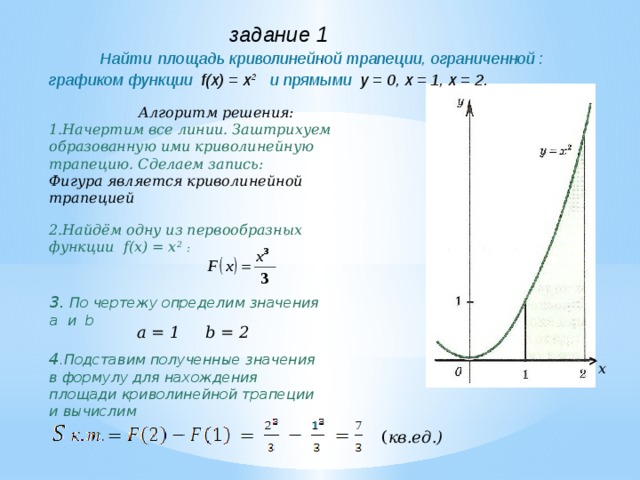
задание 1
Найти площадь криволинейной трапеции, ограниченной :
графиком функции f(x) = х 2 и прямыми у = 0, х = 1, х = 2.
,
Алгоритм решения:
1.Начертим все линии. Заштрихуем образованную ими криволинейную трапецию. Сделаем запись:
Фигура является криволинейной трапецией
2.Найдём одну из первообразных функции f(x) = х 2 :
3. По чертежу определим значения
a и b
a = 1 b = 2
4 .Подставим полученные значения в формулу для нахождения площади криволинейной трапеции и вычислим
х
( кв.ед.)

Площадь криволинейной трапеции.
Анимация по щелчку
где F(x) – любая первообразная функции f(x) .
53
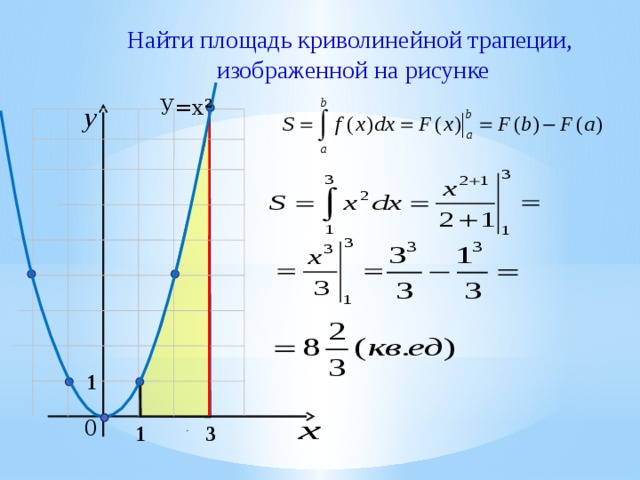
Найти площадь криволинейной трапеции,
изображенной на рисунке
У=х²
Решение – анимация по щелчку
1
0
3
1
53
I
I
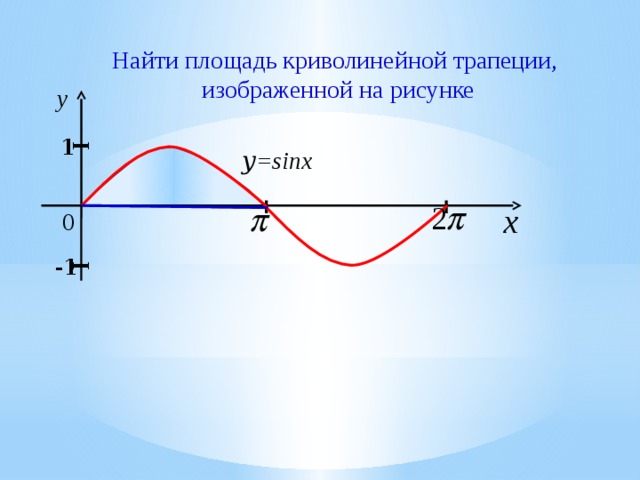
Найти площадь криволинейной трапеции,
изображенной на рисунке
1
y =sinx
0
-1
![Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b: Геометрический смысл определенного интеграла](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img58.jpg)
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:
Геометрический смысл определенного интеграла
![Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b: Геометрический смысл определенного интеграла](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img59.jpg)
- Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:
Геометрический смысл определенного интеграла
![Замечание : Если функция изменяет знак на промежутке [a;b] , то Геометрический смысл определенного интеграла](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img60.jpg)
Замечание : Если функция изменяет знак на промежутке [a;b] , то
Геометрический смысл определенного интеграла

Вычислить площадь фигуры, ограниченной линиями
Вариант 1
Вариант 2
f(x) = 2x – 3
f(x) = – 2x – 3
y = 0, x = 3, x = 5
y = 0, x = – 5, x = – 3
Сделать проверку, используя любой другой известный способ.
Вычислить площадь криволинейной трапеции, используя формулу Ньютона-Лейбница (ход решения на следующем слайде)

f(x) = 2x – 3
f(x) = – 2x – 3
Проверка
Вариант 1
Вариант 2
у
у
0 3 5 х
- 5 - 3 0 х

Используя формулу площади трапеции (геометрия)
Вариант 1
Вариант 2
f(x) = – 2x – 3
f(x) = 2x – 3
у
у
0 3 5 х
- 5 - 3 0 х
Вычисление площади трапеции с использованием формул из раздела «Геометрия»



Вычисление площадей фигур с помощью интегралов

Постановка проблемы (обобщение )
Проблема: Как с помощью интеграла вычислить площадь фигуры, не являющейся криволинейной трапецией?
Задачи на вычисление площадей фигур с помощью интеграла можно классифицировать по виду геометрических фигур, площади которых необходимо вычислить
Решение проблемы
![Классификация задач Фигура, полученная отсечением от криволинейной трапеции прямоугольника Фигура, ограниченная графиком непрерывной функции f(x)≤0 на [a;b] Фигура, ограниченная графиками непрерывных функций y=f(x), y=g(x), f(x)≥g(x) ≥0 и прямыми x=a, x=b Фигура, ограниченная графиками непрерывных функций, заданных различными формулами на различных промежутках](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img68.jpg)
Классификация задач
- Фигура, полученная отсечением от криволинейной трапеции прямоугольника
- Фигура, ограниченная графиком непрерывной функции f(x)≤0 на [a;b]
- Фигура, ограниченная графиками непрерывных функций y=f(x), y=g(x), f(x)≥g(x) ≥0 и прямыми x=a, x=b
- Фигура, ограниченная графиками непрерывных функций, заданных различными формулами на различных промежутках

Y=f(x)
Y=g(x)
Алгоритм нахождения площади фигуры
Задача : Вычислить площадь фигуры ограниченной линиями y=f(x) и y=g(x).
1. Строим (точно) график данных функций.
2. Найдём абсциссы точек их пересечения (границы интегрирования) из уравнения: f(x)=g(x).
Решаем его, находим x 1 =a, x 2 =b .
3. Выделяем свою фигуру. Выясняем, является ли данная фигура криволинейной трапецией.
4. Ищем площадь данной фигуры:
Площадь криволинейной трапеции находим по формуле Ньютона-Лейбница:
где F(x) – первообразная для f(x).
y
B
n
A
C
x
a
b

Задача №1.

Задача 1:

Задача №2.

Задача 3:

Задача 3:

Задача
Найти площадь фигуры, ограниченной линиями
y
x

1. Найдём пределы интегрирования:
2. Данная фигура не является криволинейной трапецией, следовательно, искомую площадь можно получить как разность площадей прямоугольника АBCO и криволинейной трапеции АОCBD.


Самостоятельная работа
Вариант №1 Вариант №2
Вычислите:
Вычислите площадь фигуры, ограниченной линиями

Вычисление объемов тел вращения с помощью определенного интеграла

Футбол
Устный счёт
Вычислите

Гол!!!

Вычислите

Гол!!!

Определите площадь фигуры, ограниченной линиями

Гол!!!

Молодцы!

1612 год был для жителей австрийского города Линц, где жил тогда известный астроном Иоганн Кеплер очень урожайным, особенно на виноград. Люди заготовляли винные бочки и хотели знать, как практически определить их объёмы.

Таким образом, рассмотренные работы Кеплера положили начало целому потоку исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И. Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика переменных величии заняла с этого времени ведущее место в системе математических знаний.

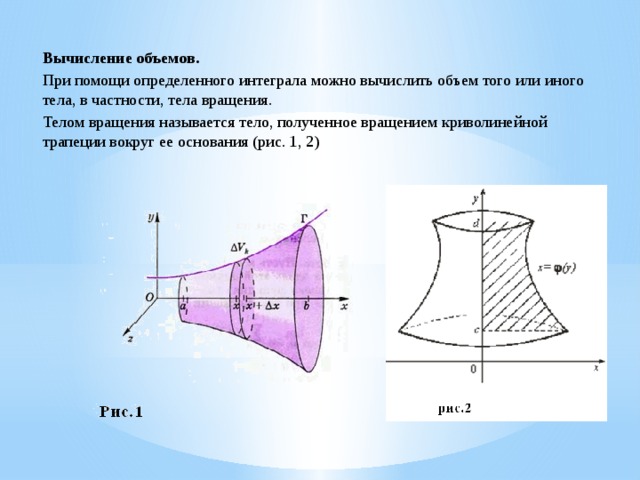
Вычисление объемов.
При помощи определенного интеграла можно вычислить объем того или иного тела, в частности, тела вращения.
Телом вращения называется тело, полученное вращением криволинейной трапеции вокруг ее основания (рис. 1, 2)

Объем тела вращения вычисляется по одной из формул :
1. , если вращение криволинейной трапеции вокруг оси ОХ ( рис. 1) .
2. , если вращение криволинейной трапеции вокруг оси ОУ ( рис. 2) .
![Объём тела, полученного в результате вращения вокруг оси x криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции y=f(x) на отрезке [a;b]:](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img92.jpg)
Объём тела, полученного в результате вращения вокруг оси x криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции y=f(x) на отрезке [a;b]:






































![Определенный интеграл (Формула Ньютона - Лейбница) Для непрерывной функции на отрезке [a;b] где F(x) – первообразная функции f(x).](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img33.jpg)













![Площадь криволинейной трапеции В декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a и графиком непрерывной неотрицательной на отрезке [a;b] функции y=f(x) , называется криволинейной трапецией](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img47.jpg)










![Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b: Геометрический смысл определенного интеграла](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img58.jpg)
![Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b: Геометрический смысл определенного интеграла](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img59.jpg)
![Замечание : Если функция изменяет знак на промежутке [a;b] , то Геометрический смысл определенного интеграла](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img60.jpg)







![Классификация задач Фигура, полученная отсечением от криволинейной трапеции прямоугольника Фигура, ограниченная графиком непрерывной функции f(x)≤0 на [a;b] Фигура, ограниченная графиками непрерывных функций y=f(x), y=g(x), f(x)≥g(x) ≥0 и прямыми x=a, x=b Фигура, ограниченная графиками непрерывных функций, заданных различными формулами на различных промежутках](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img68.jpg)























![Объём тела, полученного в результате вращения вокруг оси x криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции y=f(x) на отрезке [a;b]:](https://fsd.multiurok.ru/html/2018/03/11/s_5aa4f81a426a8/img92.jpg)










