Пирамида и конус

Пирамида, конус, их поверхность и объем.

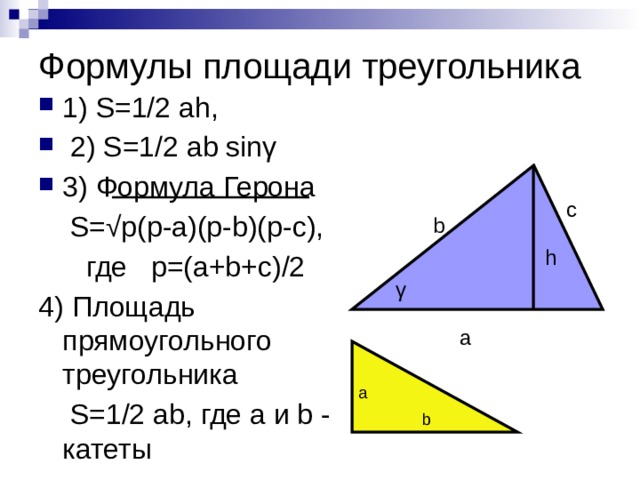
Формулы площади треугольника

• 1) S=1/2 ah,
• 2) S=1/2 ab sinγ
• 3) Формула Герона

S=√p(p-a)(p-b)(p-c),

где p=(a+b+c)/2

4) Площадь прямоугольного треугольника

S=1/2 ab, где a и b - катеты

c

b

h

γ

a

a

b

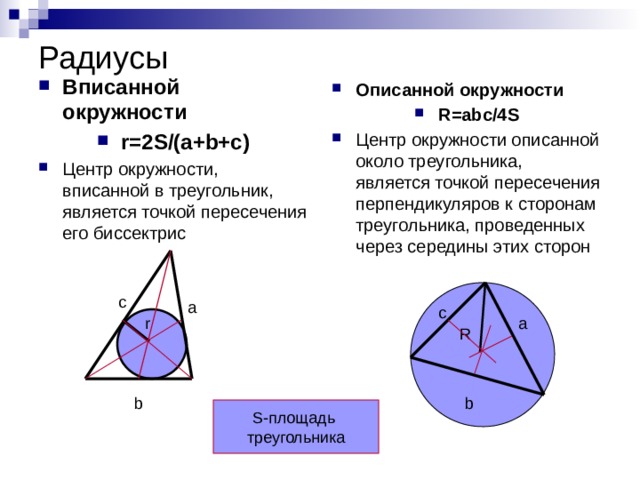
Радиусы

• Вписанной окружности
• r=2S/(a+b+c)
• Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис

• Описанной окружности
• R=abc/4S
• Центр окружности описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон

c

a

c

r

a

R

b

b

S-площадь

треугольника

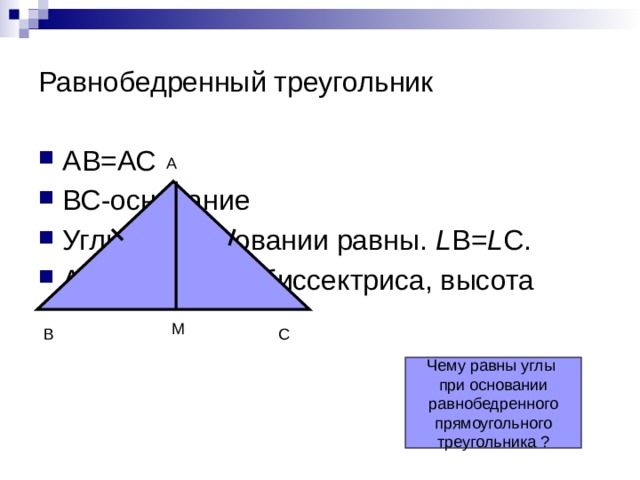
Равнобедренный треугольник

• АВ=АС
• ВС-основание
• Углы при основании равны. L В= L С.
• АМ - медиана, биссектриса, высота

А

М

В

С

Чему равны углы

при основании

равнобедренного

прямоугольного

треугольника ?

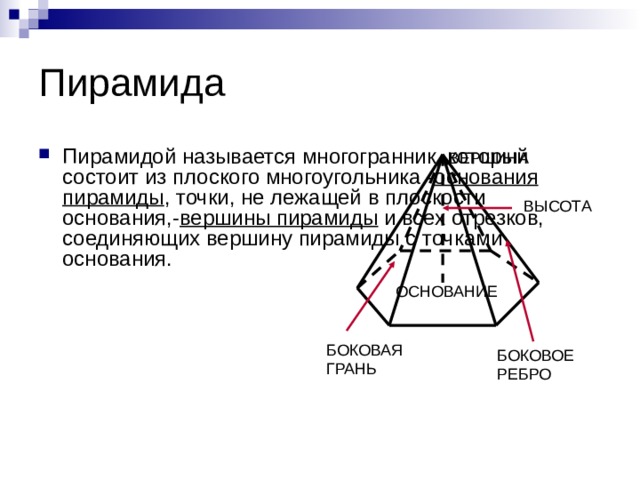
Пирамида

• Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды , точки, не лежащей в плоскости основания,- вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.

ВЕРШИНА

ВЫСОТА

ОСНОВАНИЕ

БОКОВАЯ ГРАНЬ

БОКОВОЕ РЕБРО

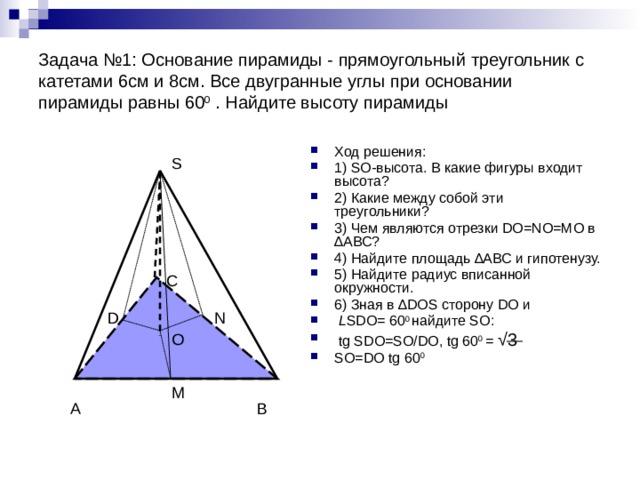
Задача №1: Основание пирамиды - прямоугольный треугольник с катетами 6см и 8см. Все двугранные углы при основании пирамиды равны 60 0 . Найдите высоту пирамиды

• Ход решения:
• 1) SO-высота. В какие фигуры входит высота?
• 2) Какие между собой эти треугольники?
• 3) Чем являются отрезки DO=NO=MO в ∆АВС?
• 4) Найдите площадь ∆АВС и гипотенузу.
• 5) Найдите радиус вписанной окружности.
• 6) Зная в ∆DOS сторону DO и
• L SDO= 60 0 найдите SO:
• tg SDO=SO/DO, tg 60 0 = √3
• SO=DO tg 60 0

S

С

N

D

O

M

В

А

Площадь поверхности и объем пирамиды

• Боковой поверхностью пирамиды называется сумма площадей ее боковых граней
• Полной поверхностью пирамиды называется сумма площадей основания пирамиды и боковой поверхности пирамиды.
• S полн =S осн +S бок
• Объем пирамиды
• V=1/3S осн h

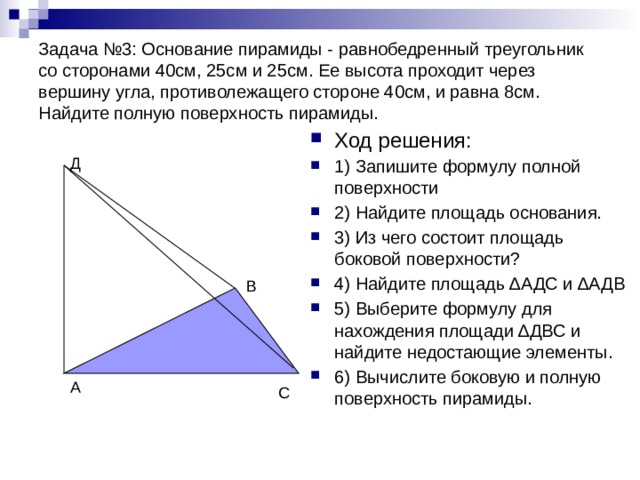
Задача №3: Основание пирамиды - равнобедренный треугольник со сторонами 40см, 25см и 25см. Ее высота проходит через вершину угла, противолежащего стороне 40см, и равна 8см. Найдите полную поверхность пирамиды.

• Ход решения:
• 1) Запишите формулу полной поверхности
• 2) Найдите площадь основания.
• 3) Из чего состоит площадь боковой поверхности?
• 4) Найдите площадь ∆АДС и ∆АДВ
• 5) Выберите формулу для нахождения площади ∆ДВС и найдите недостающие элементы.
• 6) Вычислите боковую и полную поверхность пирамиды.

Д

В

А

С

Конус

• Конусом (круговым) называется тело, которое состоит из круга -основания конуса, точки , не лежащей в плоскости этого круга, вершины конуса и всех отрезков , соединяющих вершину конуса с точками основания

Конусы вокруг нас

• Карликовое дерево

• Конусообраз-ные дома - трулли

Мороженное

Оградительные конусы

Туфовые дома (высечены в скале)

Кусты в королевском саду

Конусы - ракушки

Крыша-конус

Надувные конусы

Конус – тело вращения

• Круговой конус получается при вращении прямоугольного треугольника вокруг катета

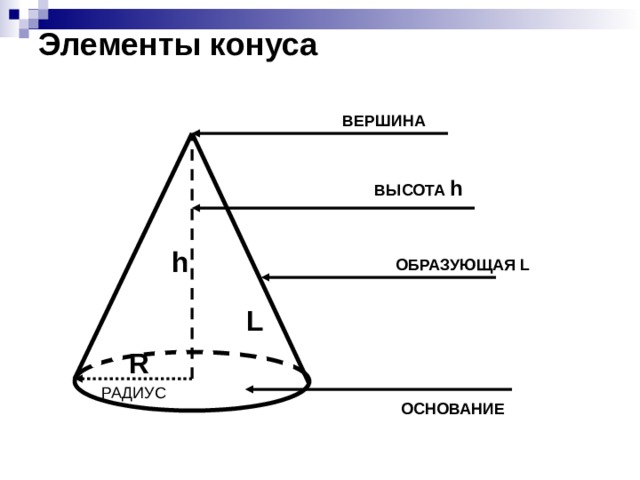
Элементы конуса

ВЕРШИНА

ВЫСОТА h

h

ОБРАЗУЮЩАЯ L

L

R

РАДИУС

ОСНОВАНИЕ

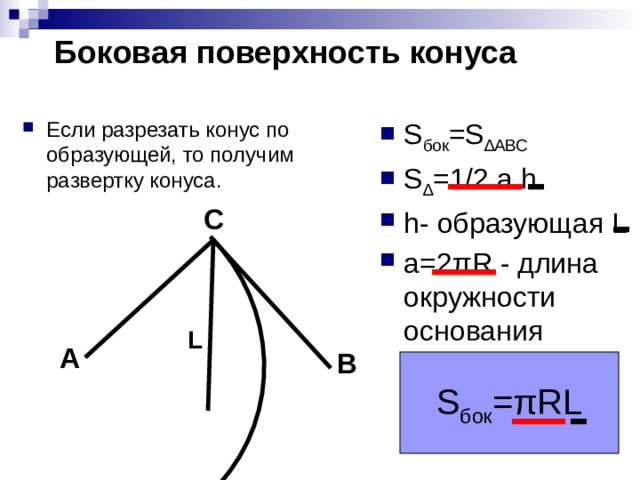
Боковая поверхность конуса

• S бок =S ∆АВС
• S ∆ =1/2 a h
• h- образующая L
• a=2πR - длина окружности основания

• Если разрезать конус по образующей, то получим развертку конуса.

C

L

A

B

S бок =πRL

Полная поверхность конуса

• Зная формулу боковой поверхности конуса выведите формулу нахождения полной поверхности конуса

R

S полн =S бок +S осн

S бок =πRL

S осн =πR 2

S полн =πRL+πR 2

S полн =πR(L+R)

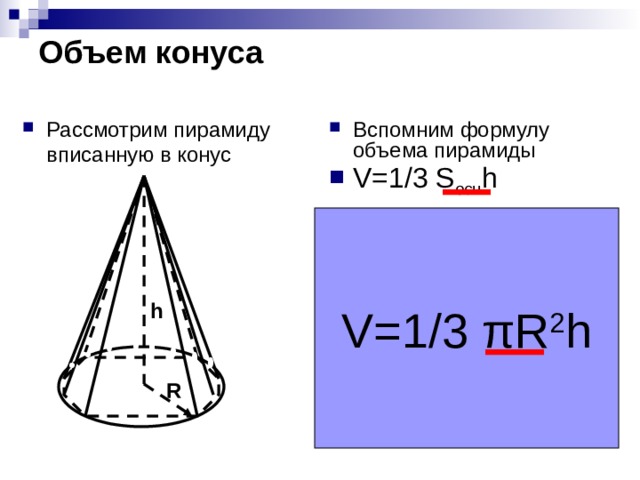
Объем конуса

• Вспомним формулу объема пирамиды
• V=1/3 S осн h

• Рассмотрим пирамиду вписанную в конус

• Чем больше сторон у основания пирамиды тем больше пирамида стремится к конусу, а площадь основания к площади круга.
• Выведите самостоятельно формулу объема конуса

V=1/3 πR 2 h

h

R

Задача №1: Конусообразная палатка высотой 3,5м с диаметром основания 4м покрыта парусиной. Сколько квадратных метров парусины пошло на палатку?

Задача №2: Стог сена имеет форму цилиндра с коническим верхом. Радиус его основания равен 2,5м, высота 4м, причем цилиндрическая часть стога имеет высоту 2,2м. Плотность сена 0,03г/см 3 . Определите массу стога сена.

• 1 . Ромб со стороной 10см и острым углом 60° вращается около большей диагонали. Найдите площадь поверхности полученного тела вращения.
• 2. Прямоугольник со сторонами 4см и 3см вращается около меньшей стороны. Найдите площадь поверхности и объем полученного тела вращения

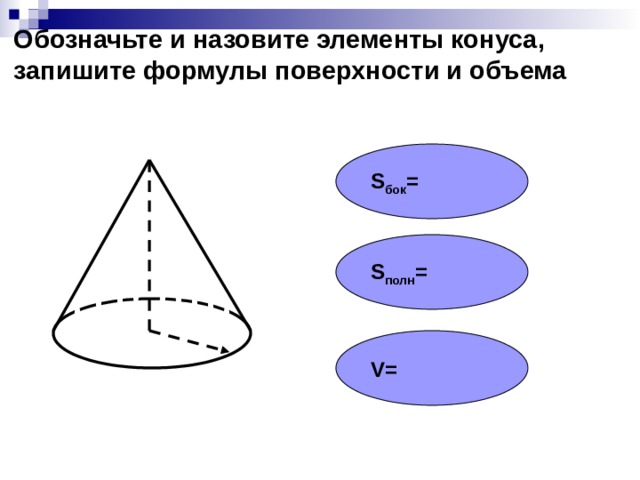
Обозначьте и назовите элементы конуса, запишите формулы поверхности и объема

S бок =

S полн =

V=

Отметьте элементы конуса на данных иллюстрациях

Образующая L

Высота h

Радиус R

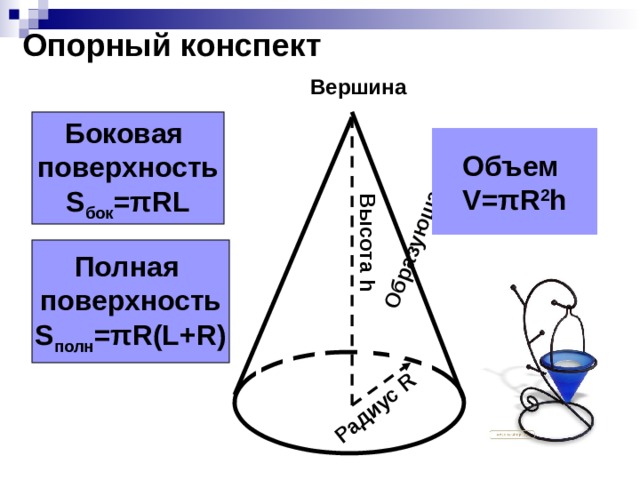
Опорный конспект

Вершина

Боковая

поверхность

S бок =πRL

Объем

V=πR 2 h

Полная

поверхность

S полн =πR(L+R)

Домашнее задание

• 1. Прямоугольный треугольник с катетом 3 см и гипотенузой 6 см вращается вокруг меньшего катета. Найдите площадь поверхности полученного тела вращения.
• 2. Прямоугольный треугольник с катетом___ см и гипотенузой ____см вращается вокруг большего катета. Найдите площадь поверхности полученного тела вращения.