Пирамида. Тетраэдр. Правильная пирамида

Тема занятия: «Пирамида. Тетраэдр. Правильная пирамида»

Перейдите по ссылке: https://egemaximum.ru/piramida/

Составьте конспект по предложенному материалу.

Ответьте на контрольные вопросы:

1. Что такое пирамида (основание пирамиды, боковые грани, ребра, высота)?

2. Что такое диагональное сечение пирамиды?

3. Какая пирамида называется правильной?

4. Что такое апофема правильной пирамиды?

5. Что такое тетраэдр?

6. Перечислите свойства пирамиды.

7. Докажите, что боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

Рассмотрите и запишите решение задачи.

Дано: SABCD - пирамида;

ABCD — прямоугольник;

SO = 12 (см); АВ = 6 (см);

ВС = 8 (см)

Найти: SD.

Решение:

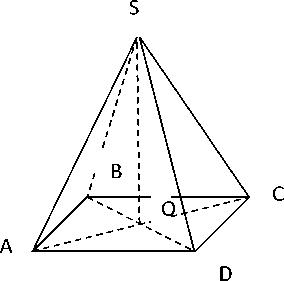
1. SO  ABCD.

2. АС и BD- диагонали прямоугольника пересекаются в точке О и делятся пополам.

1. ∆ABD - прямоугольный. По теореме Пифагора получим: BD=√АB²+AD²=√36+64=√100=10(cm)

2. ВО = OD = BD /2=10/2=5 (cm);

3. SD = SA= SB= SO боковые ребра пирамиды, т.к. ВО=OD=АО=ОС радиусы описанной окружности.

4. ∆SOD - прямоугольный треугольник. По теореме Пифагора получим: SD=√S0²+ОD²=√12²+5²=√144+25=13(cm)

Ответ: SD = 13 см.

Решите задачи самостоятельно.

Задача№1. Основание пирамиды - прямоугольный треугольник с катетами 6см и 8см. Все двугранные углы при основании пирамиды равны 60°. Найдите высоту пирамиды.

Задача №2. Высота правильной четырёхугольной пирамиды равна 7 см, а сторона основания 8 см. Найдите боковое ребро.

Задача №3. По стороне основания 6см и высоте, равной 1см, найдите апофему правильной треугольной пирамиды.

Подсказка для решения задач. При решении задач используйте свойства пирамиды и формулы для нахождения радиусов вписанной или описанной окружностей.

Сделайте рисунки правильной: а) треугольной пирамиды;

б) четырехугольной пирамиды;

в) шестиугольной пирамиды.

Погорелов А.В. Геометрия. 10-11 классы. Учебник § 5, п.47, п.50.