Тема 6.3 Основные тригонометрические тождества
Там, где заканчиваются границы привычной и давно знакомой алгебры, начинаются владения тригонометрии. Давайте вооружимся всеми необходимыми формулами, чтобы в полном обмундировании преодолеть любые тригонометрические испытания.
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin2α + cos2α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Основное тригонометрическое тождество
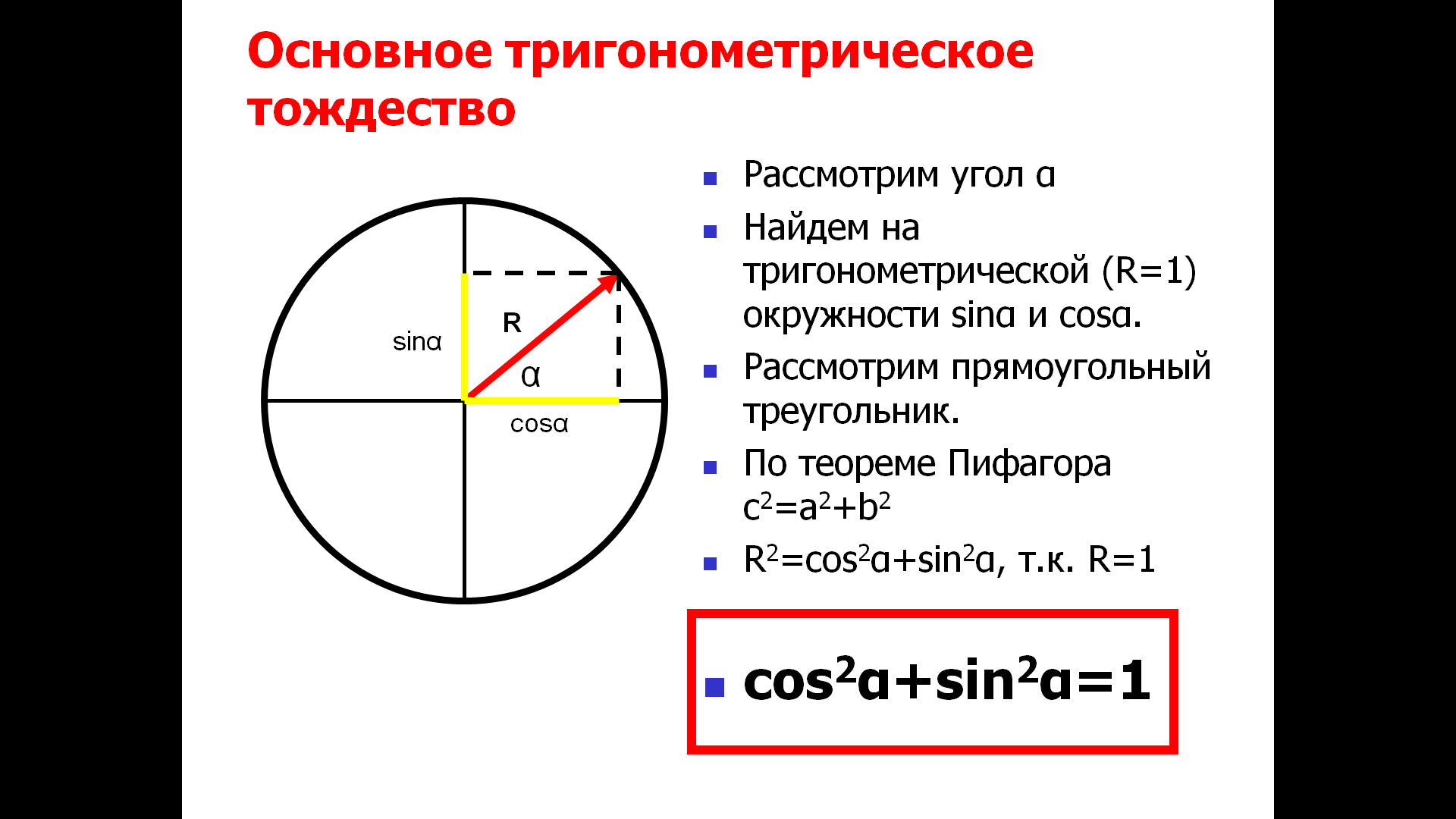
1. Построим и рассмотри единичную окружность*
2. Найдем на тригонометрической (R=1) окружности sinα и cosα.
3. Рассмотрим прямоугольный треугольник.
4. По теореме Пифагора с2=a2+b2
5. R2=cos2α+sin2α, т.к. R=1

cos2α+sin2α=1
*Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Найдите cosx, если sinx=-15/17, ππ/2
Решение:
c os2х+sin2х=1
os2х+sin2х=1
cos2х=1-sin2х
cosх=±√1-sin2х
Т. к. по условию sinx= - 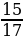
cosх=±√1-(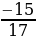 )2=
)2=
= ±√1-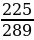 =
=
= ± √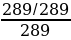 -
- 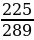 =
=
= ±√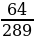 = ±
= ±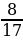
Т.к по условию . ππ/2, х-угол 3 четверти:
В 3 четверти косинус отрицателен, следовательно cosх= - 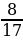 .
.
Ответ: cosх=- 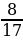 .
.
Так как найти cosx, tgx и ctgx, если sinx=-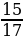 ?
?
Тангенс и котангенс через синус и косинус
Н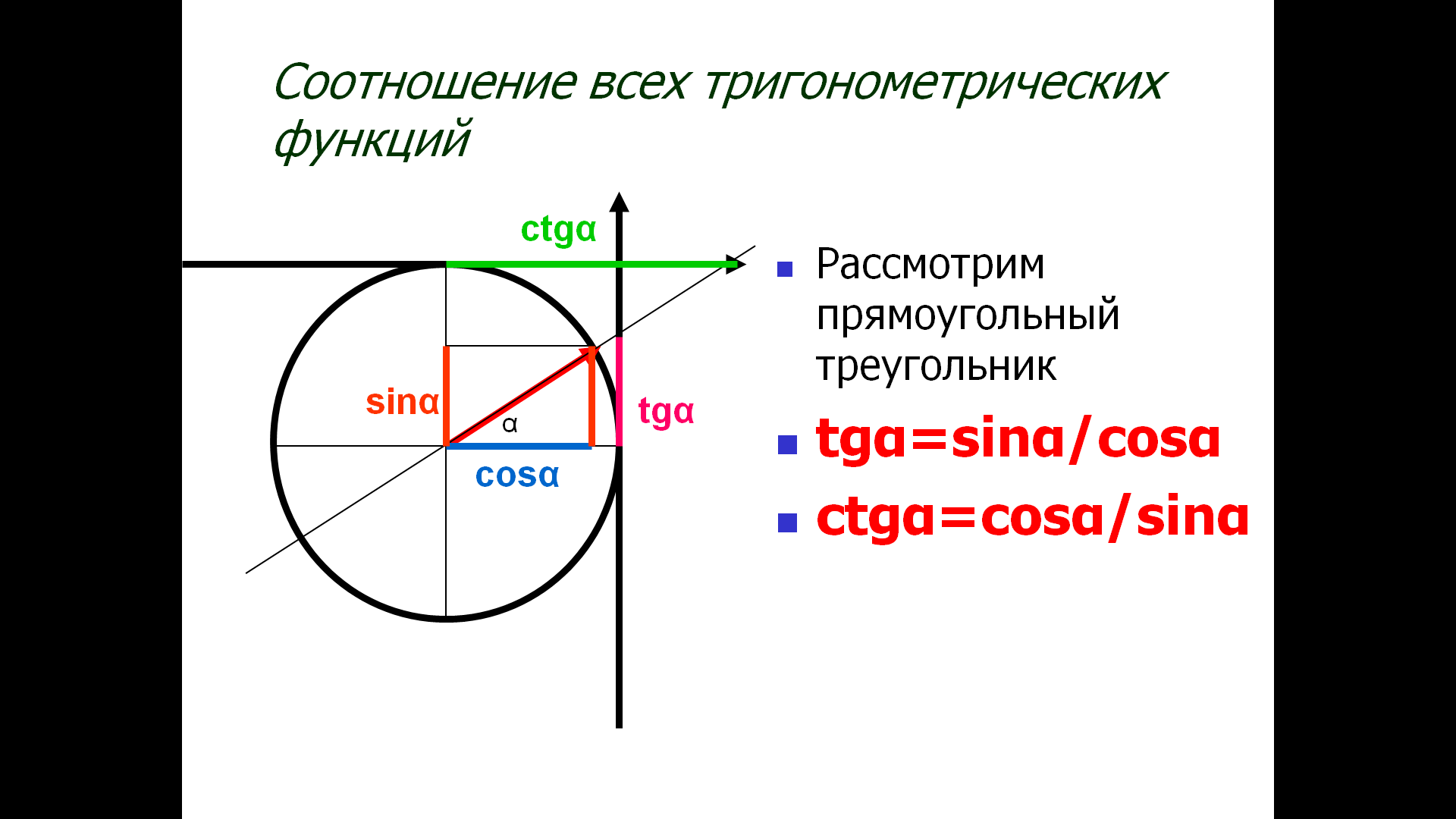 емного вводных:
емного вводных:
Синус угла — это ордината y.
Косинус угла — это абсцисса x.
Тангенс угла — это отношение ординаты к абсциссе.
Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.

tg α=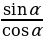
ctg α=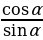
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Тождество записывается в следующем виде:
tg α * ctg α = 1
Докажете тождество: tg²x+1=1/cos²x
Доказательство: tg²x+1=1/cos²x
воспользуемся тождеством tg α=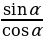
sin²x/cos²x+1=1/ cos²x
sin²x/cos²x+ cos²x /cos²x =1/ cos²x
(sin²x+ cos²x )/cos²x =1/ cos²x
вспомним основное тождество sin²x+ cos²x=1
1/cos²x =1/ cos²x
тождество доказано!
Докажите тождество самостоятельно:
ctg²x+1=1/sin²x
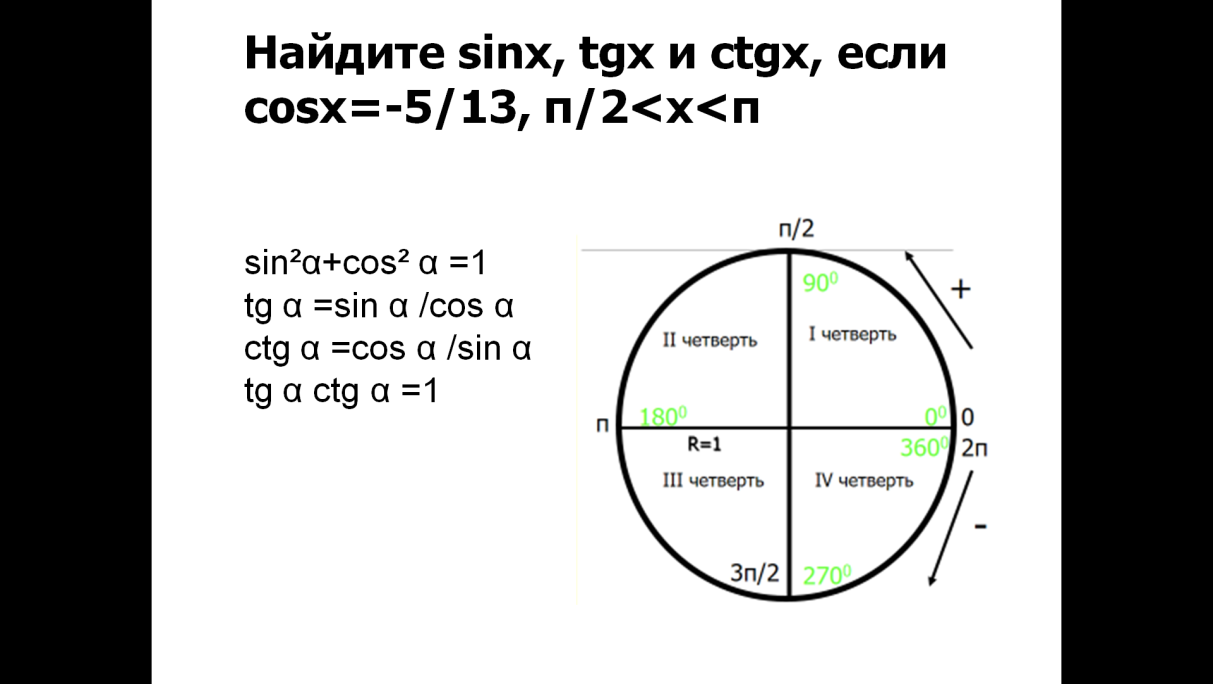
!Основные тригонометрические тождества:
sin²α+cos² α =1
tg α =sin α /cos α
ctg α =cos α /sin α
tg α ctg α =1
tg² α +1=1/cos² α
c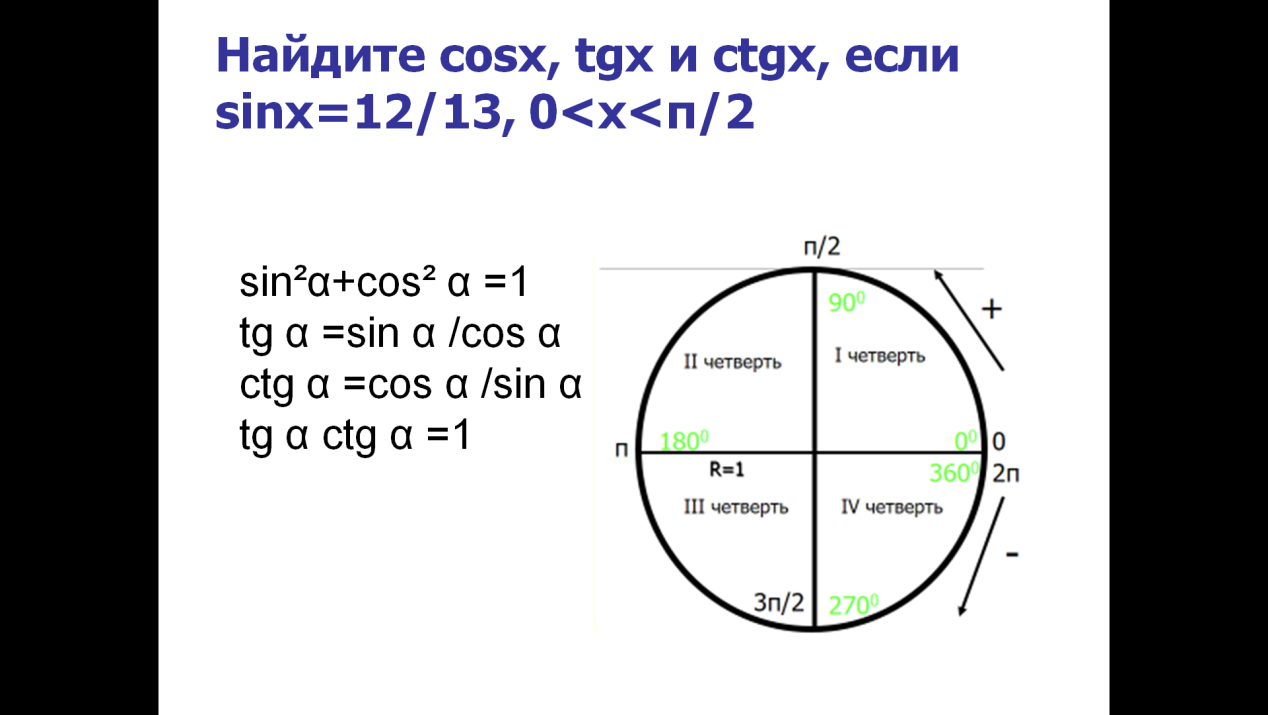 tg² α +1=1/sin² α
tg² α +1=1/sin² α
Домашнее задание: Выучить тождества. Найдите sinα, tgα и ctgα, если cosα=24/25, 3π/2π. (1) стр.53-55,стр. 66 №5










 os2х+sin2х=1
os2х+sin2х=1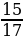
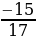 )2=
)2= 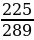 =
= 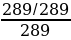 -
- 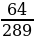 = ±
= ±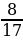
 емного вводных:
емного вводных:
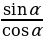
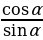
 tg² α +1=1/sin² α
tg² α +1=1/sin² α 










