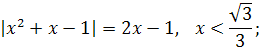План- конспект открытого урока по математике в 11 классе «Решение сложных комбинированных уравнений»

План- конспект открытого урока

по математике в 11 классе

«Решение сложных комбинированных уравнений»

Тип урока: семинарское занятие.

Цель урока:

закрепить навыки решения сложных уравнений различными методами.

Ход урока:

I Организационный момент:

а) готовность класса к уроку;

б) сообщение цели и задач урока.

ІI Актуализация опорных знаний со слабыми и средними учащимися, работа наиболее подготовленных учащихся по индивидуальным карточкам.

1. Дать определение уравнения и его корня, равносильности двух уравнений.

Ответ:

Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.

1. Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.

Ответ:

Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.

Равносильными преобразованиями уравнения являются:

• перенос члена уравнения с противоположным знаком из одной части уравнения в другую;

• умножение (деление) обеих частей уравнения на отличную от нуля число;

• возведение уравнения в нечетную степень;

• извлечение корня нечетной степени с обеих частей уравнения:

• логарифмирование показательного уравнения;

• применение тождеств, т. е равенств, справедливых для любого числа.

1. Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения:

;

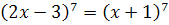1. Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.

Ответ:

Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.

Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.

При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.

Преобразованиями, приводящими к уравнению- следствия является:

• возведение уравнения в четную степень;

• потенцирование логарифмического уравнения;

• освобождение уравнения от знаменателя;

• приведение подобных членов;

• применение формул (тригонометрических, логарифмических и других).

1. Расскажите, каким способом приводится следующие уравнения к уравнению - следствия:

;

;

.

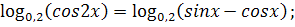
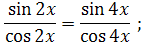
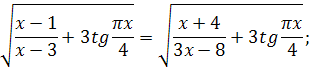
1. Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:

1.

2.

3.

4.

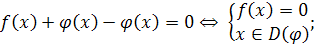
5.

6.

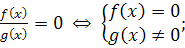
7.

М-область существования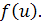 

8.

9.

10.

11. 

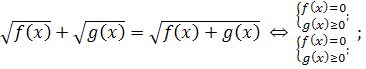
Запишите системы, равносильные уравнениям:

1.

2.

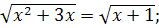
3.

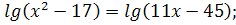
4.

5.

6.

7.

8.

9.

10.

11.

1. Решение уравнений с применением формул.

Каким способом можно решить данное уравнение:

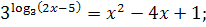
1. Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:

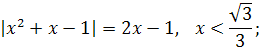
Как можно упростить решение такого типа уравнения?

Ответ:

Учитывая, что левая часть уравнения неотрицательное число получаем   значит, множество решений данного уравнения есть . Левая часть уравнения для любого   есть отрицательное число, значит, рассматривается только одно уравнение  . Решается квадратное уравнение, находим 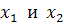 и выбираем те, которые принадлежат множеству М.

1. Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:

а)

 имеет ровно три корня.

Ответ:

Для каждого значения a рассмотрим функцию

Она определена на множестве R, четная, поэтому, если   - корень уравнения, то   - тоже является корнем уравнения.

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет   и еще два отличных от нуля корня, отличающихся знаками.

получаем: 

При   уравнение примет вид   у уравнения только один корень.

При   уравнение имеет вид 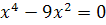 . Это уравнение имеет три корня   Ответ:3

б) Найти все значения параметра а, при которых уравнение

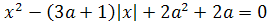. (2)

имеет ровно четыре корня.

Ответ:

Для каждого значения a рассмотрим функцию

Она определена на множестве R, четная.

Уравнение (2) имеет четыре корня, если уравнение имеет ровно два положительных корня, т.к. корнями уравнения (2) будут   . Значит дискриминант уравнения (3) должны быть положительными:

в) Для каждого значения параметра a решите уравнение:

Ответ:

При   уравнение не имеет решений, т.к.  .

При 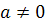  имеем:

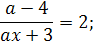
Проверяем ОДЗ:

Ответ: при  уравнение имеет одно решение

г) При каком значении параметра a уравнение не имеет корней:

Ответ:

корень уравнения.

Уравнение не имеет решений, если не выполняется ОДЗ, поэтому

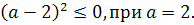
III Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.

1. 

2. ;

3. 

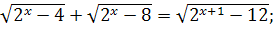
ІV Повторение. Решение заданий типа В1- В12 в интерактивном режиме с сайта www.ege.edu.ru Банк заданий типа В.

V Разбор заданий типа С с индивидуальных карточек на доске.

Карточка №1

С1.(В13)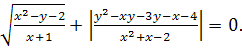 

Карточка №2

C1.(B1) 

Карточка №3

C1.(B12)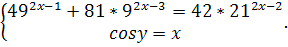 

Карточка №4

C1.(B19) 

Карточка №5

С5. Найти все значения a, такие, что уравнение имеет единственное решение:

Карточка №6

С5. Найти все значения a, такие, что уравнение имеет единственное решение:

Карточка № 7

Найти наибольший корень уравнения:

.

Карточка № 8

Найти значение р, при которых уравнение

не имеет решений.

Карточка №9

Решить уравнение

VI Домашнее задание:

1. Решить уравнения с параметром (б, г)

2. Решить № 4, 6, 9 с карточек.

3. Вариант 9 со сборника ФИПИ - разобрать В1-В12.

4. Повторить теорию по темам:

• §8 Уравнения-следствия.

• §9 Равносильность уравнений системам.

• §10 Равносильность уравнений на множествах.

VII Подведение итогов урока.

Отзыв об уроке
по алгебре и началам анализа в 11 -А классе учителя математики высшей квалификационной категории МОУ «Школа №2» города Алушта по теме «Уравнения». Дата проведения 22.11.16 года. Весна Лилия Анатольевна продемонстрировала дидактически и методически грамотный урок с высоким развивающим потенциалом. Тип урока – урок систематизации знаний и закрепления нового материала. В начале урока учитель сообщила тему и цель урока, создала благоприятный психологический микроклимат, настрой на четкую и организованную работу.
Цели и задачи урока достигнуты благодаря мастерству педагога, продуманной смене деятельности учащихся и тщательному отбору материала.
Для активации знаний учащихся (повторение видов уравнений и методов их решения) использовались принципы доступности, наглядности, научности.
Учитель мастерски вёл учащихся к цели через создание проблемных ситуаций и способы их разрешения, постоянно предлагая ученикам право выбора или несколько способов решения уравнений.
Повторение материала выстроено логично, оптимально по содержанию, разнообразно по средствам, приемам, методам обучения, способам организации учебной деятельности.
В ходе урока учитель развивает логическое мышление, интеллектуальные способности учащихся, познавательный интерес, применяя элементы современных образовательных технологий: проблемного, поисково-исследовательского, личностно-ориентированного.
Учитель умело направляет самостоятельную работу учащихся по закреплению умений решать простейшие уравнения, используя групповую форму работы, где сильный ученик помогает слабым.
Доступность материала, хороший темп урока, активность учащихся позволили учителю охватить большой объём материала: от линейных уравнений до уравнений с параметрами.
В конце занятия для отработки полученных знаний учащиеся использовали Интернет-ресурсы для подготовки к ЕГЭ: http://inf.reshuege.ru/manual - образовательный портал для подготовки к экзаменам. Выполнение тестовых заданий позволило ученикам закрепить полученные знания.
Хочется отметить партнёрский стиль общения учителя и учеников, что создаёт комфортную обстановку на уроке, позволяет учащимся свободно участвовать в обсуждении проблем, задавать вопросы, предлагать свои способы решения, проводить рефлексию своей деятельности. Урок получился интересным и методически насыщенным.
Руководитель городского МО учителей математики: Ярошко Л.Н.