План-конспект по алгебре на тему "Биквадратные уравнения"

ФИО (полностью)

Лагунова Наталья Юрьевна

Предмет

Алгебра.

Класс

9.

Тема и номер урока в теме

Уравнения приводимые к квадратным. Биквадратные уравнения.

Деятельность учителя

Деятельность учеников

I. Организационный этап

Учитель приветствует учащихся, проверяет их готовность к уроку.

Проводит инструктаж по работе с технологической картой.

Учащиеся готовы к началу работы, имеют представление о работе с технологической картой.

II Вводная беседа. Актуализация знаний.

1. Устный фронтальный опрос: (слайды №1-2).

- Чем занимались мы на предыдущих уроках?

- Что значит решить уравнение?

-Какие уравнения мы решали?

- Какие уравнения называются целыми?

2. Устная работа: (слайд 3)

1) Из предложенных уравнений выберите те, которые являются целыми

2)Каким способом можно решить каждое из предложенных уравнений.

8) (х + 4)²- 5(х + 4) = 24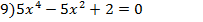

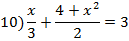
Давайте еще раз проговорим, в чем заключается способ замены переменной и разберем решение уравнения 7 на доске…

3. Решение уравнения на доске методом замены переменной:

(х + 4)²- 5(х + 4) = 24

1 Обучающиеся отвечают на вопросы устно.

2. Отвечают на вопросы:

2.1 1,2,3,5,6,7,8,9,10, уравнение 4 – не целое.

2.2 1 -метод разложения на множители

2 - метод разложения на множители

3- решение квадратного уравнения

5 - графический метод

6 - метод разложения на множители

7 – метод замены переменной

8,9,10 --------------------------

Один обучающийся решает уравнение с полным комментированием на доске, остальные в тетради.

Уравнения № 8, 9,10 не можем решить, т.к. не знаем способа решений таких уравнений, у нас недостаточно знаний…

Давайте разберем уравнение № 8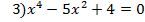

На какое уравнение похоже?

но у нас 4 степень…

давайте выделим квадрат

(х²)² – 5(х²) + 4 = 0

получили двойной квадрат… Недавно мы изучали на информатике двоичную систему счисления, и там очень часто встречалась нам какая «приставка»?

т. е. приставка БИ( от латинского bi – дву(х); bis – дважды) – часть сложных слов, указывающих на два признака, две части.

Вспомним некоторые слова с приставкой БИ

Например: Бинокль-два окуляра, два глаза.

Тогда наше «похожее» на квадратное уравнение как можно назвать?

- Давайте рассмотрим эти уравнения. Каков их общий вид?

- Что представляет собой левая часть уравнения?

- Чему могут быть равны коэффициенты? Может ли коэффициент перед х⁴ быть равен нулю? Почему?

- Чему равна правая часть уравнения?

- Какие уравнения они вам напоминают?

- В чём отличие?

- Давайте попробуем вывести определение биквадратного уравнения.

Как вы могли бы сформулировать цели урока,

тему урока?

Это и будут наши цели на урок. Запишите в тетрадь тему урока.

квадратное

можно представить 4 как 2*2

БИ, бинарные, «bin»

Возможные примеры обучающихся: Бицепс - двуглавая мыщца на руке;

Бис – повторное исполнение номера;

Биатлон –спортивное состязание, включающее 2 вида: бег на лыжах и стрельба.

БИКВАДРАТНЫМ

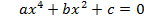
а не должно быть равно нулю.

0

квадратные

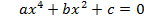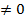Уравнение вида , где a,b,c – некоторые числа, причём а ; х – переменная называются биквадратными.

Научиться решать биквадратные уравнения.

Выработать навык решения биквадратных уравнений……

Решение биквадратных уравнений.

III. Изучение нового материала

1. Работа над выработкой алгоритма решения биквадратного уравнения (слайд).

Попробуем решить уравнение № 3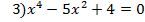

как мы с вами уже разобрали, что это уравнение можно записать (х²)² – 5(х²) + 4 = 0

Давайте попробуем его решить и составить алгоритм решения такого вида уравнений. Лист тетради разделите на 2 части – в первой будет решение уравнения, во второй части алгоритм.

Кто попробует решить уравнение и составить алгоритм?

заменим х²

Один обучающийся решает у доски с комментированием, на каждом этапе делая вывод (составляет алгоритм). Остальные – в тетради.

В итоге:

Учащиеся выполняют в технологических картах Задание №1.

Записывают план решения задания №1. Происходит обсуждение этого плана, его корректировка.

2. Первичное закрепление нового материала.

Решение уравнений на доске

Пользуясь алгоритмом решите уравнение № 9 и № 10 из устной работы, вызвавшие затруднения .

(2 человека по очереди на доске с полным комментированием)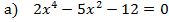

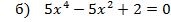
- Проведем анализ решённых уравнений. Биквадратное уравнение – это уравнение 4 степени. Сколько корней может оно иметь?

- Примеры, что уравнение имеет 4 корня, 2 корня и не имеет корней нам встретились. Как вы думаете, может ли биквадратное уравнение иметь 1 корень? 3 корня?

- Верно, если эти уравнения неполные. Приведите пример биквадратного уравнения, имеющего 1 корень.(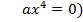

- Приведите пример биквадратного уравнения, имеющего 3 корня.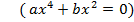

- Вернёмся к полному биквадратному уравнению. Решив предложенные уравнения выясните, от чего зависит количество корней биквадратного уравнения.

Решение каждого уравнения частично выносится на доску, а именно значение дискриминанта, значение введённой переменной и количество корней, т е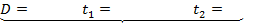

Количество корней уравнения

2 человека по очереди на доске с полным комментированием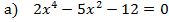

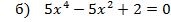
Ответы об-ся

Работа в парах.

1 ряд: Решите уравнения: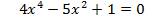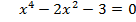

2 ряд: Решите уравнение: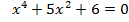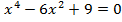

3 ряд: Решите уравнение: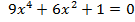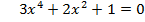

IV.Самоконтроль с самопроверкой по эталону.

Задания для самостоятельной работы:

Решите уравнение:

1 вариант: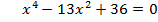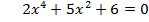

2 вариант: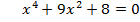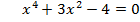

3 вариант: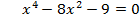

6 вариант: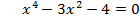

Выполните самопроверку(взаимопроверку) по готовому решению.

- Поднимите руки те, кто справился с заданием. Молодцы!

- Не огорчайтесь те, кто допустил ошибки. Помните, что не ошибается лишь тот, кто ничего не делает!

Обучающиеся решают по вариантам в тетрадях и проверяют по эталону, оценивают свою работу.

V. Этап оценивания знаний учащихся. Рефлексия.

Наш урок подходит к концу. В течение урока вы работали в картах. Оцените себя. Сосчитайте количество правильных ответов («+»). Поставьте себе оценку в соответствие с критериями):

Поднимите руку, кто получил «5», «4», «3».

Учитель выставляет оценки за работу на уроке самым активным учащимся, комментирует отметки.

Обучающиеся самостоятельно выставляют себе отметки с учетом предоставленных критериев.

Обучающиеся поднимают руки с учетом полученных оценок.

VI. Подведение итогов урока

- С каким видом уравнений мы познакомились?

- Какой общий вид они имеют?

- Каким методом решаются? Перечислите основные этапы этого метода.

- Сколько корней может иметь полное биквадратное уравнение? От чего это зависит?

Обучающиеся отвечают на вопросы учителя.

VII . Информирования учащихся о домашнем задании

Задание1:Решите уравнение:

1)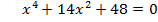

2)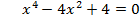

3)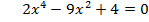

4)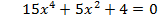

Задание 2: Подумайте, как можно решить следующие уравнения. Решите их.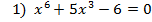

Обучающиеся записывают д\з.

Задания, которые нужно выполнить на уроке письменно.

Рекомендации учителя

Ученик ставит в эту колонку знак «+» напротив того задания, которое он выполнял вместе с классом или вместе с соседом по парте.

Ученик ставит в эту колонку «+» напротив того задания, которое он выполнял самостоятельно(быстрее, чем на доске).

Вопросы, которые возникли при выполнении задания или после выполнения задания и которые не удалось выяснить на уроке.

1.Решить уравнение

х⁴– 5х² + 4 = 0

Составить алгоритм решения уравнения.

Вспомнить алгоритм решения уравнения методом замены переменной.

2.Решить уравнение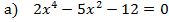

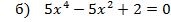
Применить алгоритм решения уравнения

№ 1.

4. Работа в парах.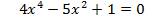

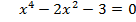
Применить алгоритм решения уравнения

№ 1.

5. Решить уравнение и сравнить с эталоном: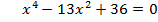

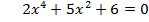
Применить алгоритм решения уравнения

№ 1.