Просмотр содержимого документа
«План конспект урока 8 класс "Понятие дробно-рационального уравнения"»
Понятие дробного рационального уравнения
Цели: Образовательные:
Активизировать знания учащихся по теме. «Понятие дробно-рационального уравнения» Использовать их при решении задач.
Развивающие:
Содействовать развитию у учащихся мыслительных операций, анализировать, сравнивать.
Воспитательная:
Вырабатывать внимание, самостоятельность при работе на уроке. Способствовать формированию активности, максимальной работоспособности
Ход урока
I Организационный момент.
Проверка домашнего задания
II Устная работа.
Решите уравнение
а)-3х²+15=0. б) 4х²+3=0.
-3х²=-15, 4х²=-3,
х²=5, х²=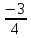 ,
,
х=±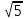 . Ответ: нет корней.
. Ответ: нет корней.
Ответ: ±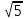 .
.
III Актуализация опорных знаний и умений учащихся:
Что такое уравнение?
Что означает решить уравнение?
Что такое уравнение?
Назовите основное свойство пропорции
IV. Объяснение нового материала.
Рациональное уравнение в котором левая и правая части являются целыми выражениями называют целым. рациональное уравнение, в котором левая и правая части являются дробными называют дробным.
Пример дробно-рационального уравнения
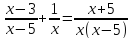 .
.
В левой части приведём к общему знаменателю, найдём область допустимых значений, данной дроби, избавимся от знаменателя дроби, получим целое уравнение: х(х-3)+х-5=х+5, после преобразования получим квадратное уравнение: х²-3х-10=0, корнями данного уравнения являются числа -2 и 5, но -5 обращает знаменатель дроби в ноль, следовательно корнем будет число -2. Выработаем алгоритм решения дробно-рациональных уравнений
| 1) Найти общий знаменатель дробей, входящих в уравнение; 2) умножить обе части уравнения на общий знаменатель; 3) решить полученное целое уравнение; 4) исключить из его корней те, которые обращают в нуль общий знаменатель. 5)существуют три способа чтобы избавится от знаменателя дроби: а) умножить левую и правую часть уравнения на знаменатель, б) приравнять знаменатели, тогда будут равными и числители, в) воспользоваться основным свойством пропорции |
V. Формирование умений и навыков.
На этом уроке отрабатывается применение алгоритма решения дробных рациональных уравнений.
1. № 600 (а, в, д, и).
Р е ш е н и е
а).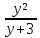 =
=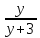 Общий знаменатель (у + 3).
Общий знаменатель (у + 3).
Умножим обе части на общий знаменатель дробей.
у2 = у;
у2 – у = 0;
у (у – 1) = 0;
у = 0 или у – 1 = 0;
у = 1.
Ответ: 0;1.
2. № 601 (а, в, г).
Можно предложить учащимся другой способ исключения посторонних корней. Как уже говорилось, при домножении обеих частей уравнения на общий знаменатель дробей, мы изменяем область допустимых значений выражений, входящих в запись уравнения. Можно тогда сперва определить ОДЗ (любые числа, кроме тех, которые обращают знаменатель в нуль), а в конце проверить, входят ли полученные корни в ОДЗ или нет.
Р е ш е н и е
№ 601.
а) 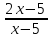 – 4 = 0; ОДЗ: х + 5 ≠ 0,
– 4 = 0; ОДЗ: х + 5 ≠ 0,
х ≠ –5.
2х – 5 – 4 (х + 5) = 0;
2х – 5 – 4х – 20 = 0;
–2х – 25 = 0;
–2х = 25;
х = –12,5.
Ответ: -12,5.
в) 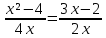 ; ОДЗ: х # 0.
; ОДЗ: х # 0.
х2 – 4 = 2 (3х – 2);
х2 – 4 = 6х – 4;
х2 – 6х = 0;
х (х – 6) = 0;
х = 0 или х – 6 = 0;
х = 6.
Ответ: 0;6.
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какое уравнение называется дробно-рациональным?
– Приведите примеры целого и дробного уравнения.
– Сформулируйте алгоритм решения дробного рационального уравнения.
– Какими способами можно исключить «посторонние» корни дробного рационального уравнения?
VII. Домашнее задание: № 600 (б, г, е), № 601 (б, е, з).






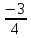 ,
,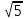 . Ответ: нет корней.
. Ответ: нет корней.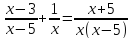 .
.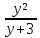 =
=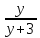 Общий знаменатель (у + 3).
Общий знаменатель (у + 3).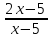 – 4 = 0; ОДЗ: х + 5 ≠ 0,
– 4 = 0; ОДЗ: х + 5 ≠ 0,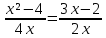 ; ОДЗ: х # 0.
; ОДЗ: х # 0.









