МЕТОДИЧЕСКАЯ РАЗРАБОТКА
План-конспект урока математики в 7-м классе по теме:
«Линейная функция и ее график»
Урок изучения нового материала
Цель урока: ознакомить учащихся с понятиями «функция», «аргумент», «линейная функция», «график линейной функции»; с построением графика линейной функции
Задачи:
образовательные:
изучить теоретический материал по теме урока;
сформировать знания учащихся по теме;
научить их строить и исследовать график линейной функции;
воспитательные:
воспитать умения и навыки групповой и самостоятельной работы;
выработать умение слушать учителя и одноклассников;
воспитывать эстетику в выполнении чертежей.
развивающие:
развивать умения анализировать учебный материал;
развивать любознательность, внимание, наблюдательность;
развивать интерес учащихся к математике, при анализе жизненных ситуаций;
формировать умение применять знания на практике.
Формы организации познавательной деятельности учащихся:
фронтальная, самостоятельная работа, работа в группах.
Оборудование урока: компьютер, колонки, интерактивная доска.
Этапы урока:
I. Организационный момент (2 мин).
II. Подготовка к основному этапу занятия (6 мин).
III. Изучение нового материала (7 мин).
IV. Закрепление темы. (7 мин.)
V. Самостоятельная работа (8 мин).
VI. Физкультминутка (1 мин).
VII. Работа в группах (5 мин).
VIII. Итоги урока (1 мин).
IX. Информация о домашнем задании (1 мин).
X. Выставление оценок и их комментирование (1 мин).
XI. Рефлексия (1 мин).
Ход урока:
Организационный момент.
Приветствие, проверка присутствующих. Объявление целей и задач урока.
На уроке изучаем новый материал по теме «Линейная функция и ее график». Учащиеся задают вопросы по домашней работе. Обсуждение наиболее проблемных заданий. Дежурные собирают тетради с домашней работой и раздают тетради с оценками. Заранее на доске записана тема урока и домашнее задание.
Подготовка к основному этапу занятия.
Девиз урока: « Подобно тому, как дар слова обогащает нас мнением других, так язык математических законов служит средством еще более совершенным, более точным и ясным…»
Н. И. Лобачевский.
Используя формулу пути S=vt, найдите устно неизвестную величину:
| V = 0,5км/ч T = 6 ч. S = ? | S = 12 км V = 3км/ч t = ? | V = 97км/ч t = 8 ч. S =? | S= 100 м t = 11 мин. V= ? |
Вычислите:  ,
,  ,
,  ,
,  .
.
Дано линейное уравнение с двумя переменными. Используя его, выразите каждую переменную через другую:
а) x + y = 23; в) 5a + b = 70;
б) m – n = 46; г) 4s – 8t – 32 = 0.
III. Изучение нового материала (9 мин).
Историческая справка. ( Краткая информация на интерактивной доске)
| 
| Николай Иванович Лобачевский (1792-7856) расширил понятие функции, используя способы задания функции: формулой, графиком или словесным испытанием.
|
| 
| Рене Декарт впервые в математике стал рассматривать буквы как переменные. Идея функции возникла вместе с понятием переменной и была тесно связана с геометрическими и физическими представлениями.
|
| 
| Впервые термин «функция» использовал Готфрид Лейбниц (1646-1716), который первым ввёл термин «абсцисса» - в 1695г., «ордината» - в 1684г., «координаты» - в 1692г. |
| 
| Исаак Ньютон (1643-1727) рассматривал изменения физических величин в зависимости от времени. Рене Декарт (1596-1650) – изменение ординаты точки от изменения ординаты абсциссы, т.е. y от х
|
| 
| В XVI - XVII вв. французский математик Франсуа Виет ввел буквенное обозначение для чисел.
|
Учитель обобщает материал по теме, используя таблицы, спроецированные на доску.
Что необходимо знать о линейной функции?
Вспомним алгоритм построения графика линейного уравнения ах + bу + c = 0.
Придать переменной х конкретное значение х₁; найти из уравнения
ах + bу + c = 0 соответствующее значение у₁. Получим (х₁;у₁).
Придать переменной х конкретное значение х2; найти из уравнения
ах + bу + c = 0 соответствующее значение у2. Получим (х2;у2).
Построим на координатной плоскости точки (х₁; у₁), (х₂; у₂) и соединим прямой.
Прямая – есть график уравнения.
Внимание! Этот способ не удобен!
Выполним преобразования: ах + bу + c = 0.
bу = – ах – c,
y =  ,
,
y = –  x–
x–  ,
,
Обозначим: –  = k, –
= k, –  = m.
= m.
Получим: y = kx + m – частный вид линейного уравнения с двумя
переменными называемый линейной функцией.
х – аргумент (независимая переменная)
у – функция (зависимая переменная)
k, m – числа (коэффициенты), к  0
0
Функция задаётся:
1) формулой: у = kx + m
2) парами: (х1; у1), (х2; у2)
3) таблицей:
4) графиком:

График функции y = kx + m , при к0
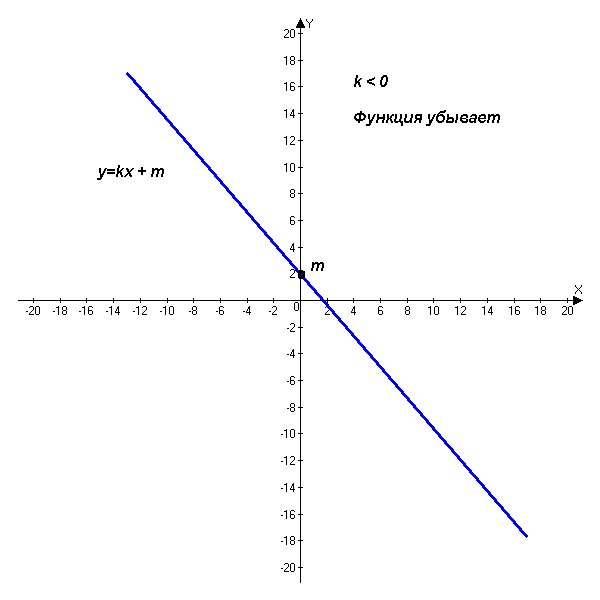
График функции y = kx + m , при к0
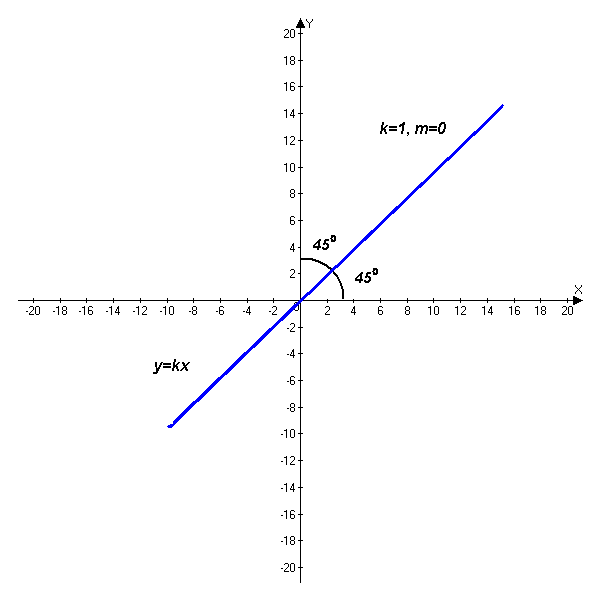
График функции y = kx
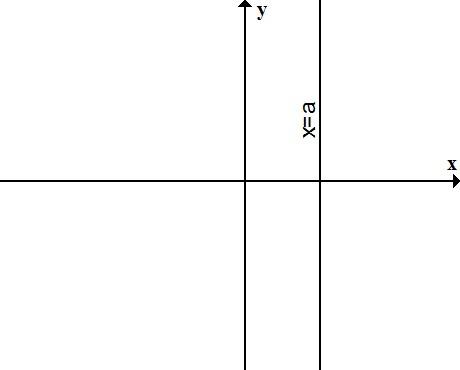
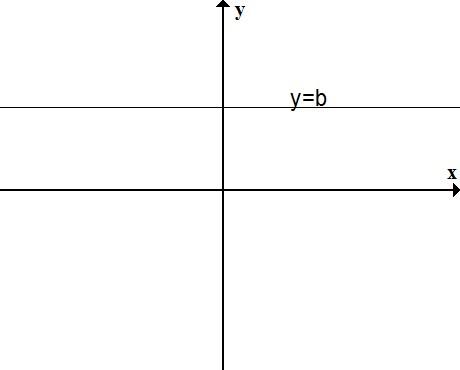
График функции х=а График функции у=b
ось ординат ось абсцисс
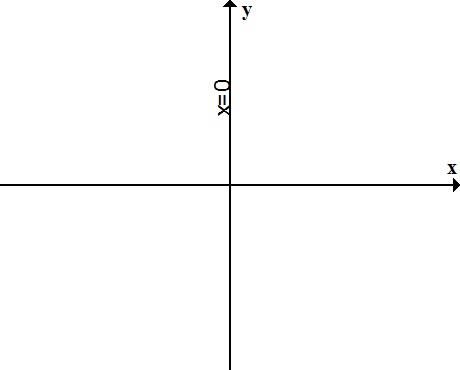
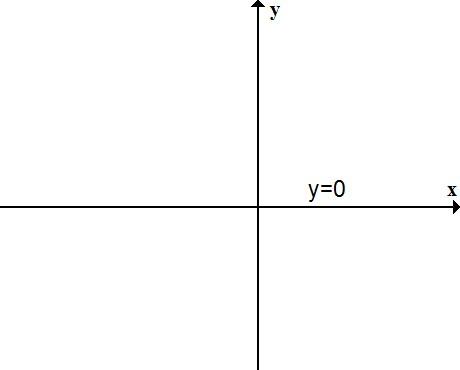
График функции х=0 График функции у=0
IV. Закрепление темы.
(Пять учащихся выходят к доске и выполняют задание. Оценки за работу
можно выставить по желанию).
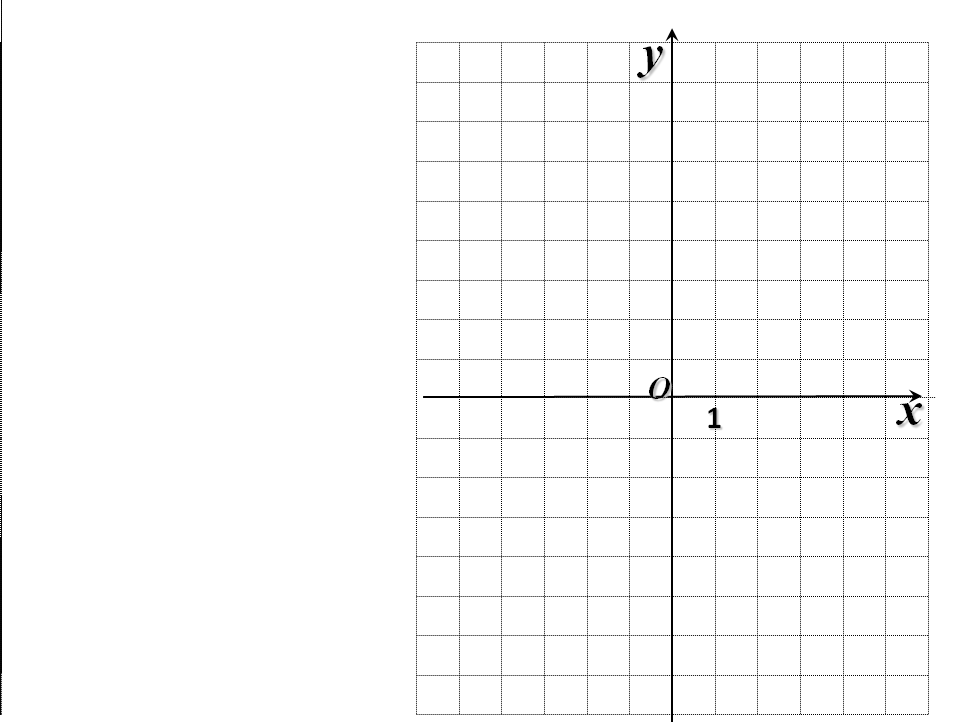
Построить график функции у = 2х + 3, найти точку пересечения с осью оу.
Решение.
а) составим таблицу значений
y(0) = 2  0 + 3 = 3,
0 + 3 = 3,
y(1) = 2  1 + 3 = 5.
1 + 3 = 5.
б) получим точки: (0;3), (1;5);
в) построим эти точки и через них проведем прямую;
г) если k = 2 0, то линейная функция у = kx + b, возрастает;
д) точка пересечения с осью оу: (0; 3) т. е. при m = 3.

Построить график функции у = - 2х + 1, х -3; 2
Решение.
а) составим таблицу значений
y(0) = - 2

(- 3) + 1= 7 ,
y(1) = - 2  2 + 1 = - 3.
2 + 1 = - 3.
б) получим точки: (-3;7), (2;-3),
в) построим эти точки и через них проведем прямую,
г) выделим отрезок х -3; 2,
д) если k = - 2  0, то линейная функция у = kx + b, убывает,
0, то линейная функция у = kx + b, убывает,
е) точка пересечения с осью оу: (0; 1) т. е. при m = 1.


Построить график функции у = - 2х + 1, х (-3; 2)
Решение.
а) составим таблицу значений
y(0) = - 2

(- 3) + 1= 7 ,
y(1) = - 2  2 + 1 = - 3.
2 + 1 = - 3.
б) получим точки: (-3;7), (2;-3),
в) построим эти точки и через них проведем прямую,
г) выделим интервал х (-3; 2),
д) если k = - 2  0, то линейная функция у = kx + b, убывает,
0, то линейная функция у = kx + b, убывает,
е) точка пересечения с осью оу: (0; 1) т. е. при m = 1.





Найти наибольшее и наименьшее значение функции y =  + 4 на отрезке 0; 6.
+ 4 на отрезке 0; 6.
Решение.
а) составим таблицу значений
y(0) =  + 4 = 4 ,
+ 4 = 4 ,
y(6) =  + 4 = 7.
+ 4 = 7.
б) получим точки: (0;4), (6;7),
в) построим эти точки и через них проведем прямую,
г) выделим отрезок х 0; 6,
д) если k = 0,5 0, то линейная функция у = kx + b, возрастает;
е) точка пересечения с осью оу: (0; 4) т. е. при m = 4.



ж) найдем наибольшее и наименьшее значение функции на отрезке
0; 6: yнаиб = 7, yнаим = 4.
Построить график функции у =  3.
3.
Решение.
а) при любом значении аргумента значение функции равно одной и той
же величине у =  3.
3.
б) точки: (-1; -3), (2; -3) принадлежат графику функции у =  3,
3,
в) построим эти точки и через них проведем прямую.

y =  3
3

V. Самостоятельная работа (разноуровневая)
|
I вариант |
|
| 1. Выберите функцию, которая является линейной: | |
1. у = х3- 5 |
2. у =  |
3. у = - 6х + 5 | 4. у =  х2+3 х2+3
| |
|
|
|
| | 2. Дана функция: у = -11х + 4,3, укажите коэффициент k.
| | 1. – 4,3 | 2. 4,3 | 3. 10 | 4. - 11
| |
|
|
|
| | 3. Дана функция: у = 7х – 8,1, укажите значение m .
| | 1. 1 | 2. 8,1 | 3. 7 | 4. - 8,1 | |
| | 4. Укажите формулу, задающую линейную функцию при k = 4; m = -5.
| | 1. у = 4х - 5 | 2. у = -5х + 4 | 3. у = 5х – 4 | 4. у = х.
| |
| | 5. Дана функция: у = 2х – 6, найдите значение функции при х = 2.
| | 1. 10 | 2. - 6 | 3. - 2 | 4. 0 | | 6. Дана функция: у = 4х + 3, найдите значение аргумента, если значение функции равно 7.
| | 1. 28 | 2. - 28 | 3. -1 | 4. 1
|
|
| II вариант
| 1. Выберите функцию, которая является линейной: | |
1. у = 3 + х3 |
2. у = 3х+8
|
3. у =  |
4. у = х2 | | 2. Дана функция: у = - 8х + 5, укажите коэффициент k
| | 1. 5 | 2. 8 | 3. - 8 | 4. - 5
| | 3. Дана функция: у = 9х - 12, укажите значение m.
| | 1. 12 | 2. - 12 | 3. 9 | 4. - 9
| | 4. Укажите формулу, задающую линейную функцию при k = 1; m = -6.
| | 1. у = - х | 2. у = х - 6 | 3. у = - 6х + 1 | 4. у = - 6х + 5.
| | 5. Дана функция: у = 4х – 13, найдите значение функции при х = 3.
| | 1. 1 | 2. 26 | 3. - 1 | 4. 0
| | 6. Дана функция: у = 3х + 15, найдите значение аргумента, если значение функции равно 3
| | 1. 24 | 2. 0 | 3. 4 | 4. - 4 |
|
| III вариант Найдите наибольшее и наименьшее значение линейной функции на заданном промежутке: а) у = - 2x + 5, 0; 4, б) у = 3x – 5, - 1; 1. 2. Постройте график линейной функции у = 3x – 6 и сего помощью решите уравнение 3x – 6 = 0.
|
У читель объявляет, что оценки по самостоятельной работе будут выставлены на следующем уроке.
VI. Физкультминутка.
Гимнастика для глаз
Ах, как долго мы писали.
Ах, как долго мы писали, Глазки у ребят устали.
(Поморгать глазами.) Посмотрите все в окно,
(Посмотреть влево - вправо.) Ах, как солнце высоко.
(Посмотреть вверх.) Мы глаза сейчас закроем,
(Закрыть глаза ладошками.) В классе радугу построим, Вверх по радуге пойдем,
(Посмотреть по дуге вверх- вправо и вверх - влево.) Вправо, влево повернем, А потом скатимся вниз,
(Посмотреть вниз.) Жмурься сильно, но держись. (Зажмурить глаза, открыть и поморгать им.)
VII. Работа в группах.
Возвращаясь к ходу урока, учитель делит класс на три группы: 1) учащиеся с высокой мотивацией к учебе; 2) учащиеся со средним уровнем знаний; 3) учащиеся с низким уровнем знаний. Вторая и третья группы получают задания (задача №1, задача №2). Задания дифференцированные, соответствуют уровню знаний учащихся, каждой группы. Первая группа учащихся является экспертами, они выполнили решение задач заранее, как домашнее задание к этому уроку. Они ассистируют и консультируют. В конце выполнения заданий они оценивают работу учащихся из каждой группы.
Задача №1. Постройте график функции у = x + 4. Найдите координаты точек пересечения графика с осями координат.
Задача №2. Постройте график функции у = - 4x + 8.
а) Найдите значение функции, соответствующее значению аргумента, равного 0.
б) Найдите значение аргумента, соответствующее значению функции, равной 4.
Итоги урока.
1. Учащиеся из первой группы опрашивают учеников из второй и третьей
групп по теме урока «Линейная функция и ее график».
Что такое линейное уравнение?
Что такое линейная функция?
Как построить график линейной функции?
Итог урока – игра. Составьте математическую модель ситуации: «Турист проехал на автобусе 20 км от пункта А до пункта В, а затем продолжил движение из пункта В в том же направлении, но уже пешком, со скоростью 3 км/ч. На каком расстоянии от пункта А будет находиться турист через 1 ч, 3 ч, 5 часов ходьбы?»
Информация о домашнем задании. Задание на доске.
1. Решить № 8.33, 8.35. Учебник по алгебре. 7 класс. Авторы учебника
Мордкович А.Г., Александрова Л.А., Мишустина Т.Н.
2. Подготовить сообщение на слюбую из следующих тем:
Понятие функции в математике до XVII в.
Функция вокруг нас.
Значение функции в жизни человека.
Функция в жизни физики и геометрии.
Выставление оценок и их комментирование.
Первая группа оценивает работу учащихся второй и третьей группы, аргументируя свои решения. Затем учитель дает свои комментарии по поводу оценок, в том числе оценивая работу сильных учащихся.
Рефлексия.
Учитель предлагает учащимся выбрать смайлик из предложенных трех вариантов которые лежат на парте.
Рис. №1 – тема несложная. Я легко справлюсь с домашним заданием.
Рис. №2 – тема сложная, но мне достаточно ещё раз самому сесть и прочитать параграф учебника. Почитать конспекты. Выполнить вдумчиво домашнее задание.
Рис. №3 – тема очень сложная, и мне нужна дополнительная работа с учителем по этой теме.
Поднимите тот, который ближе всего отражает ваше настроение в конце урока.

Рис. №1. Рис. №2. Рис. №3.
13






 ,
,  ,
,  ,
,  .
.




 ,
, x–
x–  ,
, 0
0

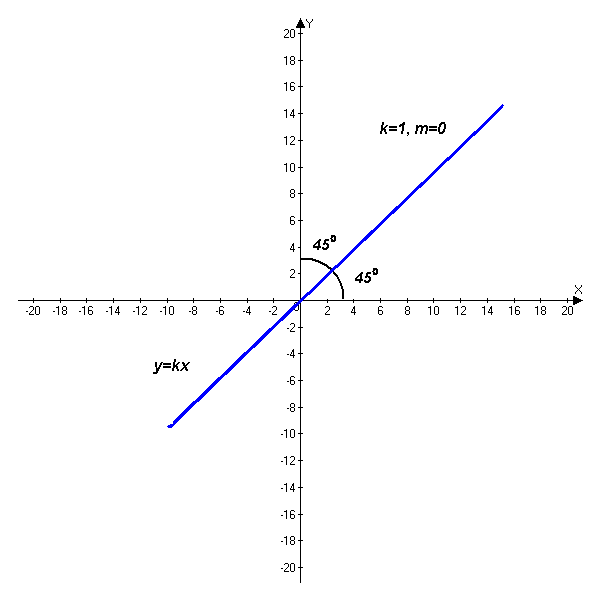




 0 + 3 = 3,
0 + 3 = 3,










