План - конспект урока по физике в 11 классе по теме "Энергия связи атомных ядер"

Подготовила и провела: учитель физики Сосновской сош №2 Тепикина Л.Ф.

В ядре существуют силы особой природы — ядерные силы, которые действуют между нуклонами на расстояниях, сравнимыми с размерами самих ядер, и препятствуют взаимному электростатическому отталкиванию между протонами в ядре. Следовательно, чтобы расщепить ядро на отдельные нуклоны, не взаимодействующие между собой, необходимо совершить работу по преодолению ядерных сил. Другими словами, сообщить ядру определённую энергию.

Так вот, минимальная энергия, необходимая для расщепления ядра на отдельные нуклоны, называется энергией связи. Чем она больше, тем стабильнее ядро. Из закона сохранения энергии следует, что энергия связи равна той энергии, которая выделяется при образовании ядра из отдельных частиц.

Самый простой способ определения энергии связи основан на одном замечательном законе природы, устанавливающим соотношение между массой тел и их энергией. Из этого закона следует, что изменение массы тела влечёт за собой изменение энергии этого тела. При этом даже ничтожному изменению массы тела соответствует значительное изменение энергии.

Энергию связи любого ядра можно определить с помощью точного измерения его массы. С изобретением масс-спектрографов физики получили возможность измерять массы микрочастиц с очень высокой точностью. Эти измерения показывают, что масса любого ядра всегда меньше суммы масс входящих в его состав протонов и нейтронов:

М_я Zm_р + Nm_n.

Разность между суммарной массой всех нуклонов ядра в свободном состоянии и массой ядра, называют дефектом массы:

ΔM = Zm_р + Nm_n – М_я.

В качестве примера рассмотрим ядро атома гелия-4. Это химический элемент 18-й группы первого периода системы химических элементов Менделеева, с атомным номером два.

В соответствии с соотношением Эйнштейна между массой и энергией, дефект массы характеризует энергию связи атомного ядра:

E_св = ΔMс² = (Zm_р + Nm_n – М_я)с².

Обращаем ваше внимание на то, что при использовании данной формулы, массу входящих в неё частиц следует выражать в килограммах. Тогда значение полученной энергии связи будет выражено в джоулях. Здесь же обратим ваше внимание на то, что энергия связи ядра намного порядков превышает энергию связи электронов с атомом (энергию ионизации). Поэтому при расчётах энергию связи электронов с атомом обычно не учитывают.

4 этап: Закрепление нового материала

Давайте теперь для примера рассчитаем энергию связи ядра изотопа гелия-4.

5 этап: Обобщение нового материала

Как видим, энергии микромира крайне малы и работать с такими числами представляется крайне неудобным. Гораздо проще рассчитывать энергию связи в электронвольтах и мегаэлектронвольтах.

Давайте вспомним, что 1эВ равен энергии, необходимой для переноса элементарного заряда в электростатическом поле между точками с разницей потенциалов 1 В. Проще говоря, величина одного электронвольта равна значению элементарного заряда в джоулях. Но энергии связи таковы, что для их вычисления удобно использовать миллионы электронвольт, то есть мегаэлектронвольты.

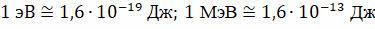
В этом случае массу частиц лучше всего выражать в энергетических единицах. Связь между различными единицами массы:

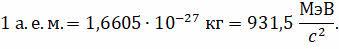
В этом случае формула для определения энергии связи примет вид:

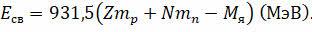
Обратите внимание на тот факт, что обычно в таблицах приводятся массы атомов, а не массы ядер. Поскольку при таком подходе учитываются и массы электронов, то для вычисления энергии связи ядра в этом случае целесообразно преобразовать формулу так, чтобы в неё входила не масса ядра, а масса соответствующего атома. Для этого вспомним, что масса ядра есть разность между массой атома и массой всех его электронов. Преобразуем формулу для дефекта масс с учётом последнего уравнения.

В полученном выражении первым слагаемым у нас стоит произведение зарядового числа на сумму масс протона и электрона. В природе существует единственный элемент, в ядре которого находится один протон, а вокруг ядра вращается один электрон — это атом водорода. Поэтому формула для дефекта масс примет вид, показанный на экране:

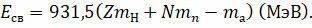
Ещё одной важной характеристикой в ядерной физике является удельная энергия связи. Так называют энергию связи, приходящуюся на один нуклон. Она равна отношению энергии связи к массовому числу:

приходящуюся на один нуклон. Она равна отношению энергии связи к массовому числу:

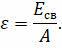
Соответственно, чем больше значение удельной энергии связи, тем сильнее связан каждый нуклон в ядре, и тем прочнее ядро.

Энергию, выделяющуюся или поглощающуюся в процессе таких ядерных реакций, можно определить, если известны массы взаимодействующих и образующихся в результате этого взаимодействия ядер и частиц. Эту энергию называют энергетическим выходом ядерной реакции. При этом, если в процессе ядерной реакции энергия выделяется, то реакцию называют экзотермической, если же энергия поглощается — то эндотермической:

∆𝐸 = 𝐸₀ – 𝐸.

6 этап : Домашнее задание

п. 55, ответить на вопросы после параграфа

7 этап: Итог урока