ПЛАН-КОНСПЕКТ УРОКА
Тип урока: Закрепление изученного материала
Тема: "Треугольник"
Цели:
образовательные: закрепить понятие о треугольниках и их элементах, показать практическое решение задачи;
развивающие развивать логическое мышление, умение высказывать свои мысли, пространственное представление;
воспитательные: воспитание навыков самоконтроля и взаимоконтроля, правильной самооценки, умения работать в паре; воспитание самостоятельности учащихся через организацию индивидуальной деятельности;
Оборудование: Оборудование: учебник Геометрия 7-9 классы Л.С. Анатасян, В.Ф. Бутузов, С.Б. Кадомцев и др., плакат с заданиями для письменной работы, треугольники из бумаги.
Структура урока
1. Организационный момент (2 мин).
2. Проверка домашнего задания (5мин).
3. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний (4 мин).
4. Ознакомление с новым материалом (10 мин).
5. Отработка действий, входящих в состав овладения понятием (5 мин).
6. Упражнения на закрепления понятия равнобедренных треугольников (11 мин).
7. Подведение итогов урока (2 мин).
8. Рефлексия (4 мин).
9. Постановка домашнего задания (2 мин).
ХОД УРОКА
Организационный момент
Учитель: Здравствуйте ребята. Сегодня на уроке мы посетим удивительную страну Геометрия.
Звучит высказывание Галилео Галилея:
«Геометрия является самым могущественным средством для изощерения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать». А теперь проверьте все ли готово у вас к путешествию: дневник, учебник, тетрадь, ручка, линейка, чертежный треугольник, цветные карандаши.
Ученики: Да!
Учитель: Тогда в путь!
Проверка домашнего задания
Тема прошлого урока: решение задач.
Формулировка домашнего задания:
1. Прочитать §2, выучить п.16,17. На стр. 49-50 ответьте на вопросы с 1-9.
2. Решить задачи из учебника Стр. 33- 34, № 101, 102, 106
№101
Начертите треугольник. С помощью масштабной линейки отметьте середины сторон и проведите медианы треугольника.

Рис.21
В ∆ABC – AM, BD,CE – высоты.
№102
Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.

Рис.21
В ∆ABC – BK, AL,CN – биссектрисы.
№103
Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол М тупой. С помощью чертёжного угольника проведите высоты каждого треугольника.
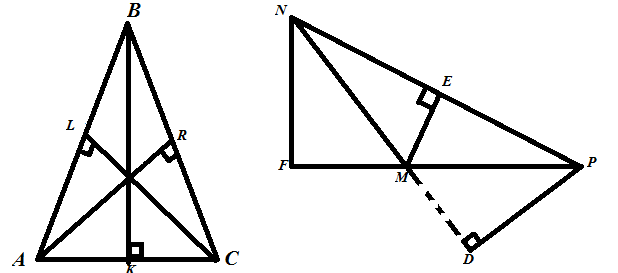
Рис.22
В ∆ABC – BK, AR,CL – высоты
В ∆MNP – ME,NF,PD – высоты.
Форма проверки: ученики меняются тетрадями и для примера учитель берёт одну и сверяют ответы. Останавливаются на тех задачах, которые большая часть класса не сделала.
Актуализация знаний, необходимых для решения задачи
Один из методов её решения требует от учащихся владения следующими видами деятельности: Можно предложить выполнить следующие задания (или тест)
Тест
Какой из предложенных треугольников равносторонний.



А) Б) С)
2. Какие из свойств принадлежат равностороннему треугольнику?
А) Все углы равны, любая медиана этого треугольника является биссектрисой и высотой.
Б) Медиана, проведённая к основанию, является биссектрисой и высотой.
В) Сумма острых углов равна 90°.
3.Определите углы ∠KML и ∠KMN на рис.1, если луч ML является биссектрисой угла ∠KMN.
Известно, что ∠NML=11°

рис.1
А) 11 и 22
Б) 10 и 21
В) 11 и 20
4. Выберите из предложенных правильное утверждение для рис.2
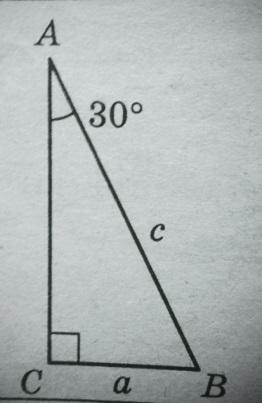
рис.2
А) Все углы равны
Б) Острые углы равны острым углам треугольника
В) Против угла 30° лежит катет, равный половине гипотенузе
5. Определите чему равен ∠B на рис.3.

Рис.3
А) 60°
Б) 30°
В) 90°
6. Выберите правильное утверждение, для рис.4
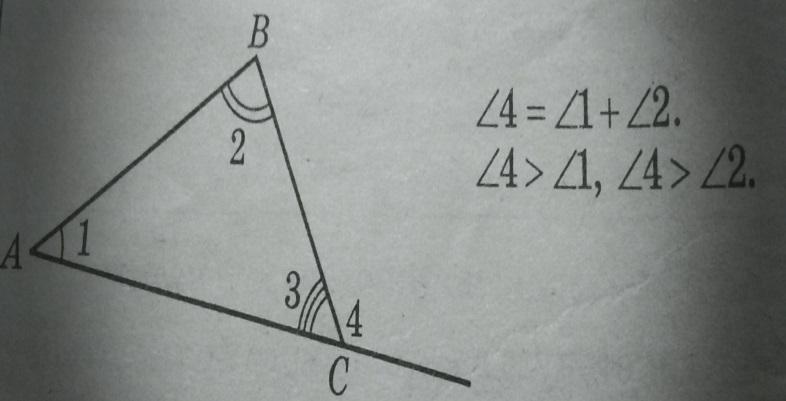
Рис.4
А) Соответственные углы равны
Б) Сумма углов треугольника равна180°
В) Внешний угол равен сумме двух внутренних углов, не смежных с ним.
4. Изучение содержания задачи. Интерпретация задачи

5. Поиск метода решения задачи
Поиск метода решения задачи можно осуществить, например, путём организации следующего диалога:
Учитель: Итак, давайте с вами посмотрим на наш равносторонний треугольник, давайте найдём чему равны углы в нашем треугольнике?
Ученики: 60°.
Учитель: Да, а как вы это нашли?
Ученики: Сумма углов треугольника равна 180°, а в равностороннем треугольнике углы равны, поэтому 180°:3=60°.
Учитель: А теперь давайте посмотрим на наши биссектрисы, что они образовали при пересечении?
Ученики: Треугольники.
Учитель: Давайте, теперь посмотрим на биссектрису CD, чем она ещё является для треугольника ABC?
Ученики: Медианой и высотой.
Учитель: Правильно, а высота CD падающая на сторону BA образовывает угол в …?
Ученики: 90°.
Учитель: Да и это мы с вами нашли ∠ODA. Давайте посмотрим на треугольник ADO, какой он?
Ученики: Прямоугольный.
Учитель: Давайте с вами найдём ∠OAD, давайте посмотрим, что у нас для этого есть?
Ученики: углы, которые равны по 60°.
Учитель: Правильно, мы уже знаем градусную меру угла А.
Какое свойство нам может помочь найти угол?
Ученики: Свойство биссектрис делящих угол пополам.
Учитель: И это так, ∠OAD равен половине угла А. Так чему будет равен наш угол?
Ученики: 30°.
Учитель: Правильно, мы уже знаем два угла в ∆ADO, и теперь мы можем найти угол ∠DOA. Как мы можем это сделать?
Ученики: По теореме о сумме углов в треугольнике 180°-(90°+30°)=60°.
Учитель: Вот мы и нашли ∠DOA.
Давайте теперь давайте запишем наше решение пошагово.
5-6. Составление плана решения задачи. Реализация плана решения задачи (диалог с учениками)
| № п/п | План решения задачи | Реализация плана решения задачи |
| 1. | Найти углы равностороннего треугольника | 180°:3=60° |
| 2. | Применили свойство равностороннего треугольника.
Нашли ∠ODA | Любая биссектриса равностороннего треугольника является биссектрисой и высотой. А значит CD падающая на сторону BA образовывает угол в 90°. Это ∠ODA. |
| 3. | Применим свойство биссектрис Находим ∠OAD | Биссектриса делит углы пополам, значит ∠OAD= ∠А =30°. ∠А =30°. |
| 4. | Находим ∠DOA по свойству углов в треугольнике. | По теореме о сумме углов в треугольнике 180°-(90°+30°)=60°. |
Учащимся предлагается граф-схема решения задачи.

7. Проверка решения задачи
По теореме о сумме углов в треугольнике сложим полученные углы
90°+30°+60°=180°.
8. Поиск других способов решения задачи
Учитель: Итак давайте с вами обратим внимание на треугольник AOC, образованный с помощью биссектрис АK и CD, и посмотрим на ∠DOA. Каким углом является DOA для AOC?
Ученики: Внешним.
Учитель: А что мы знаем про внешний угол?
Ученики: Внешний угол равен сумме двух внутренних углов, не смежных с ним.
Учитель: А значит сумме каких двух углов равен ∠DOA?
Ученики: ∠DOA=∠OAC+∠OCA
Учитель: А мы знаем, что биссектриса делит углы пополам, значит ∠OAC и ∠OCA равны?
Ученики:30°.
Учитель: А ∠DOA равен?
Ученики: 60°.
9. Обобщение (или конкретизация) задачи
Биссектрисы AK и СD равностороннего треугольника АВС пересекаются в точке O. Найти:∠OСA.
10. Применение задачи
В жизни такая задача прежде всего может быть полезна для определения
местонахождения объектов в море, океане…
А также можно встретить в определении расстояния разных пунктов.
7. Рефлексия
Ученики становятся по кругу и учитель предлагает сыграть в игру воображаемый мячик, чьё имя называет, к тому и летит мячик. К кому прилетает мячик, тот высказывается одним предложением
1. Я научился…
2. Было трудно…
3. Сегодня я узнал…
4. У меня получилось…
5. Теперь я могу…
8. Подведение итогов.
Учитель: Мы с вами сегодня были в чудесной стране Геометрии и что же мы там узнали?
Учитель: Молодцы! А теперь выставим оценки ( учитель выставляет оценки ученикам, аргументируя за что).
9. Постановка домашнего задания.
1. Изучить п.18 с доказательством теорем, ответить на вопросы 10-12 на стр.48.
2. Решить задачи №104, 107
В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр равен 50 см. Найдите стороны треугольника.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Геометрия 7-9 классы: учеб. для общеобразоват. организаций /
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. – М.: Просвещение, 2016.
Геометрия. 7 – 9 кл. : учеб. для общеобразоват. учреждений / И.Ф. Шарыгин. – М.: Дрофа, 2012. – 452, [2] c.: ил.
Самостоятельные и контрольные работы по алгебре и геометрии, 7 класс, Ершова А.П., Ершова А.С., Голобородько В.В., 2013.















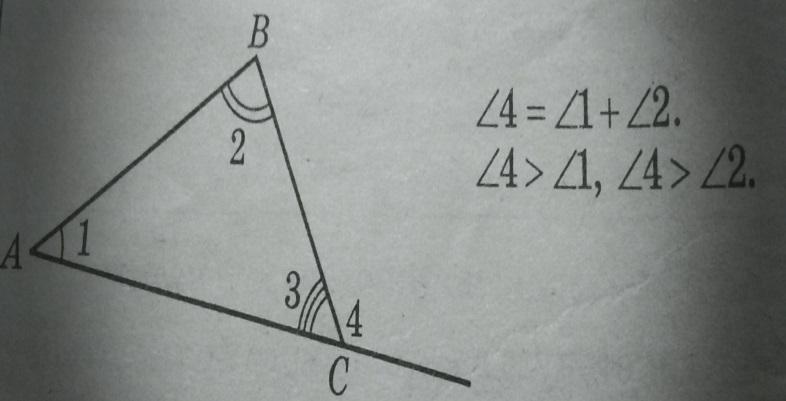

 ∠А =30°.
∠А =30°.










