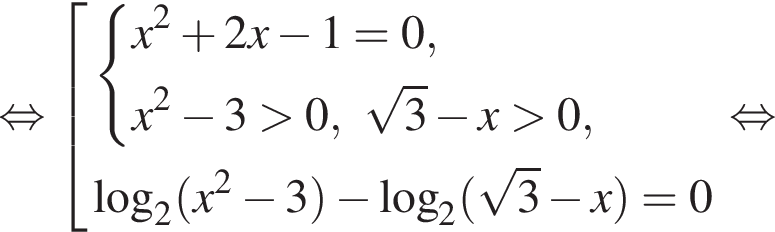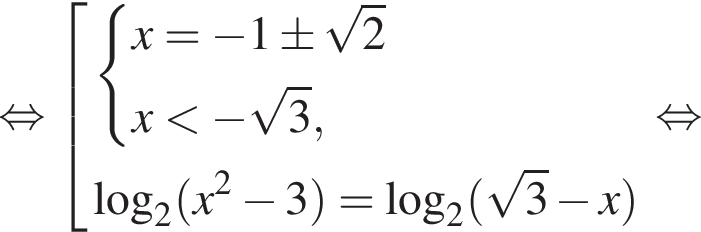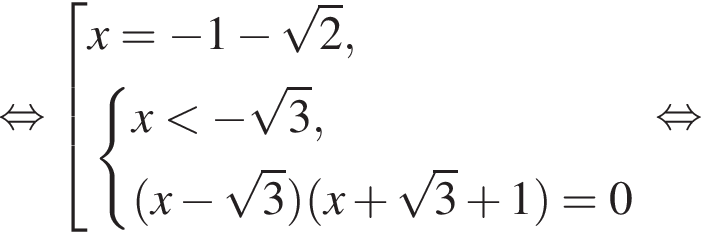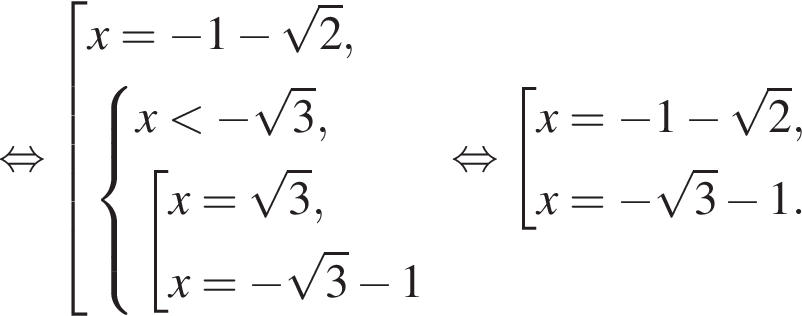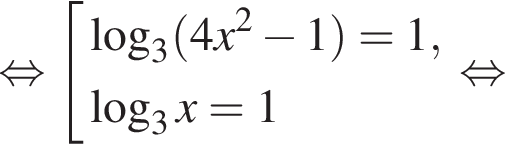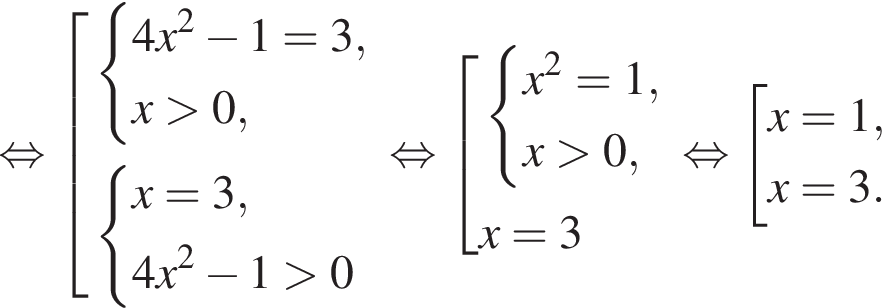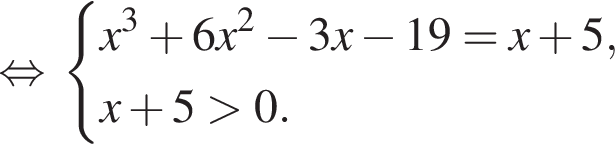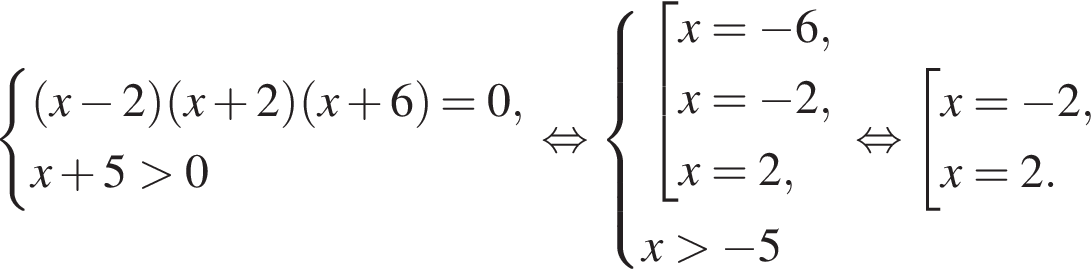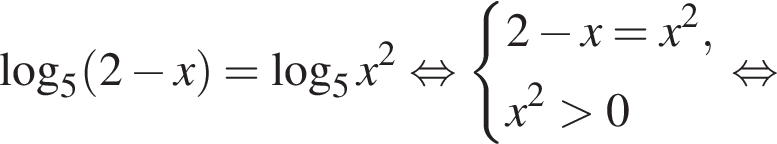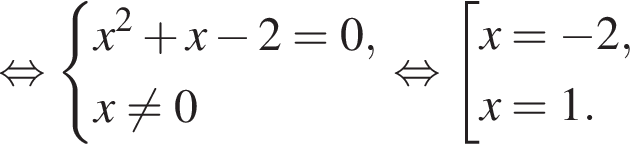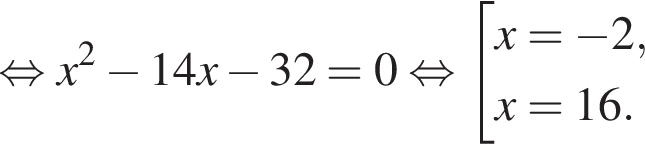Конспект урока-консультации по теме: «Логарифмы. Логарифмические уравнения»
Цели урока:
Образовательная цель: обеспечить в ходе урока сознательное повторение определения логарифма и его свойств. Умение применять эти свойства при решении различных типов логарифмических уравнений. Показать необходимость глубоких знаний по данной теме на более сложных уравнениях.
Воспитательная цель: воспитывать сознательное отношение к учебе, повышение интереса к математике, к исследовательской работе.
Развивающая цель: развивать логическое мышление, математическую речь, умение сравнивать и делать выводы; совершенствовать навыки работы со свойствами логарифмов и применять их при решении уравнений.
Ход урока
I. Организационная часть
приветствие
подготовка учащихся к уроку
получение сведений об отсутствующих.
П. Повторение материала
logab
а = b, а 0, а≠1 , b 0. Как называется это равенство?
Дописать свойства логарифмов на доске пока остальные отвечают устно
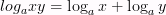
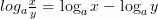
loga xn = n · loga x 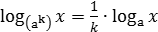
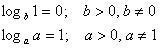
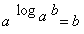
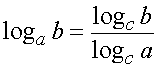
3) Какие логарифмы называются десятичными, натуральными?
4) Дайте определение логарифмической функции.
5) Какие область определения и область значения функции у = logax?
6) В каком случае функция у = logax является возрастающей, в каком убывающей?
7) Дайте определение логарифмического уравнения.
2.Историческая справка.
Джону Неперу принадлежит сам термин «логарифм», который он перевел как «искусственное число». Джон Непер – шотландец. В 16 лет отправился на континент, где в течение пяти лет в различных университетах Европы изучал математику и другие науки. Затем он серьезно занимался астрономией и математикой. К идее логарифмических вычислений Непер пришел еще в 80-х годах XVI века, однако опубликовал свои таблицы только в 1614 году, после 25-летних вычислений. Они вышли под названием «Описание чудесных логарифмических таблиц».
Вычислить устно
1.1. Тип 7 № 4491 
Найдите значение выражения 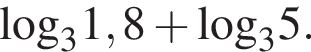
Ответ: 2
2.2. Тип 7 № 26843 
Найдите значение выражения 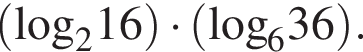
Ответ: 8
3.5. Тип 7 № 26846 
Найдите значение выражения 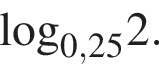
Ответ: -0,5
4.6. Тип 7 № 26847 
Найдите значение выражения 
Ответ: 1,5
5.7. Тип 7 № 26848 
Найдите значение выражения 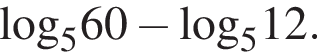
Ответ: 1
Найдите значение выражения 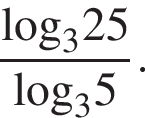
Ответ: 2
6.11. Тип 7 № 26852 
Найдите значение выражения 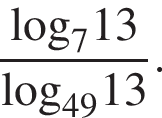
Ответ: 2
7.15. Тип 7 № 26856 
Найдите значение выражения 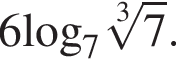
Ответ: 2
8.16. Тип 7 № 26857 
Найдите значение выражения 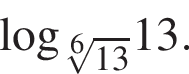
Ответ: 6
9.20. Тип 7 № 26861 
Найдите значение выражения 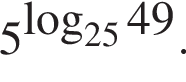
Ответ: 7
10. 22. Тип 7 № 26882 
Найдите значение выражения 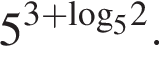
Ответ: 250
Решение уравнений 1 часть
1.5. Тип 6 № 26657 
Найдите корень уравнения 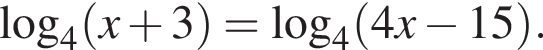
Ответ: 6
2.6. Тип 6 № 26658 
Найдите корень уравнения 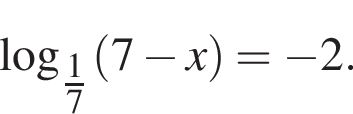
Ответ: -42
3.7. Тип 6 № 26659 
Найдите корень уравнения 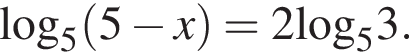
Ответ: -4
8. Тип 6 № 77380 
Решите уравнение 
Ответ: 5
4.9. Тип 6 № 77381 
Решите уравнение 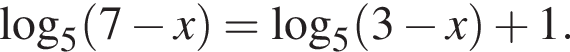
Ответ: 2
5.10. Тип 6 № 77382 
Решите уравнение 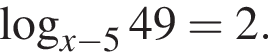 Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Ответ: 12
6.11. Тип 6 № 315120 
Найдите корень уравнения 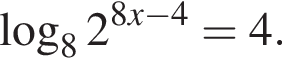
Ответ: 2
7.12. Тип 6 № 315535 
Найдите корень уравнения 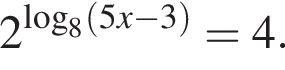
Ответ: 13,4
2 часть
1.3. Тип 13 № 514623 
а) Решите уравнение 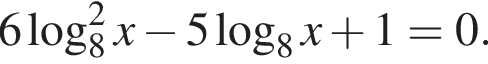
б) Найдите все корни этого уравнения, принадлежащие отрезку 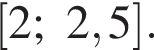
Решение. а) Запишем исходное уравнение в виде:
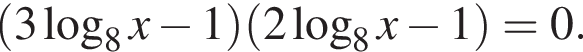
Значит, 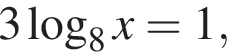 откуда
откуда  или
или 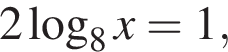 откуда
откуда 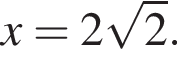
б) Заметим, что 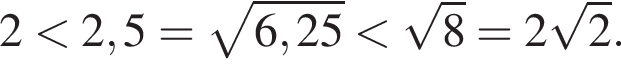
Значит, указанному отрезку принадлежит корень 2.
Ответ: а) 2 и  б) 2.
б) 2.
Пока про запас
4. Тип 13 № 502053 
а) Решите уравнение 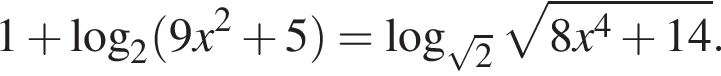
б) Найдите все корни этого уравнения, принадлежащие отрезку 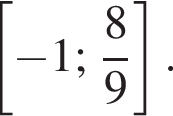
Решение. а) Заметим, что уравнение определено при любом 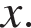 Запишем исходное уравнение в виде:
Запишем исходное уравнение в виде:
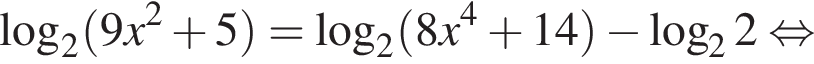


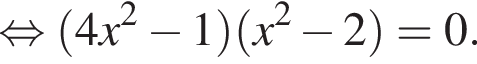
Значит, либо 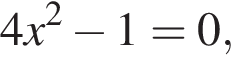 откуда
откуда 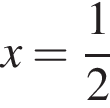 или
или 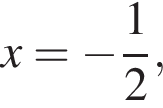 либо
либо 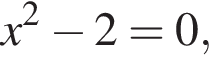 откуда
откуда  или
или 
б) Поскольку 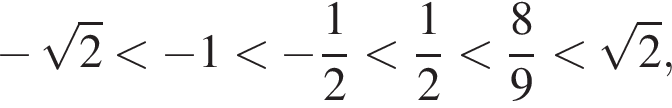 отрезку
отрезку 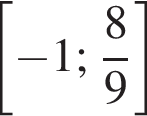 принадлежат корни
принадлежат корни 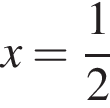 и
и 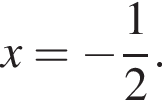
Ответ: а) 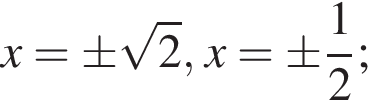 б)
б) 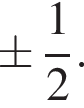
5. Тип 13 № 525377 
а) Решите уравнение 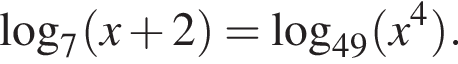
б) Найдите все корни этого уравнения, принадлежащие отрезку 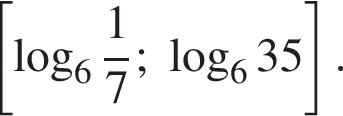
Решение. а) Поскольку  получаем:
получаем:
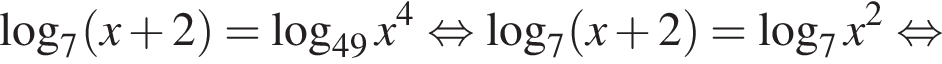
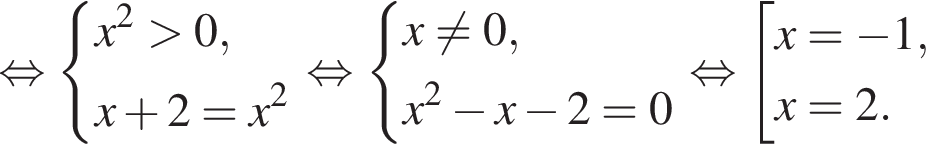
б) В силу цепочки соотношений 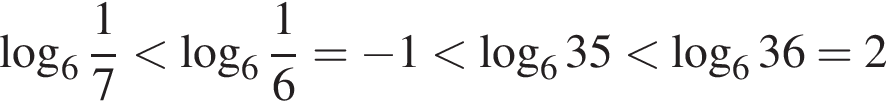 заданному отрезку принадлежит только число −1.
заданному отрезку принадлежит только число −1.
Ответ: а) {−1, 2}, б) −1.
6. Тип 13 № 550261 
а) Решите уравнение 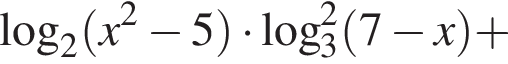
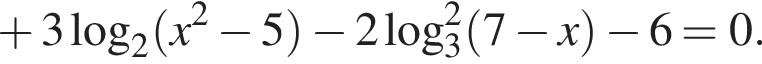
б) Укажите корни этого уравнения, принадлежащие промежутку 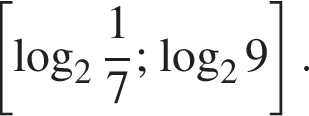
Решение. а) Преобразуем уравнение:
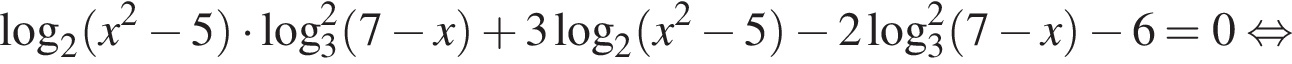
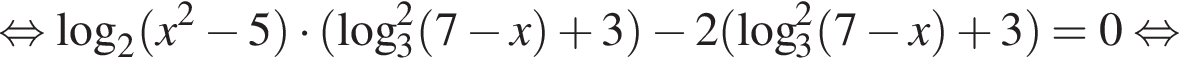
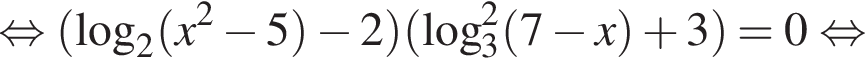
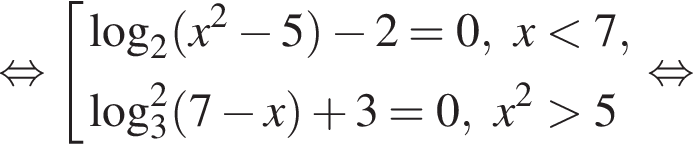
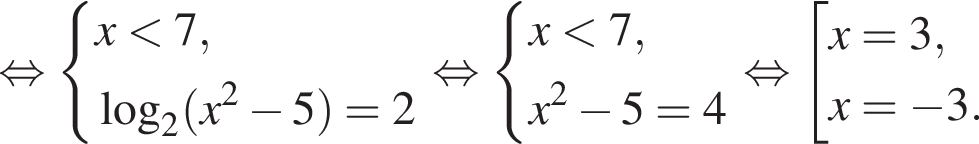
б) Заметим, что
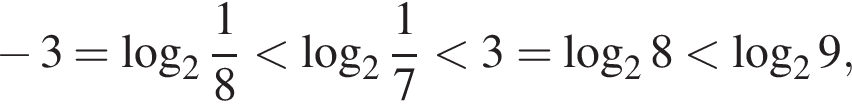
поэтому в указанный промежуток попадает только корень 
Ответ: а) {−3; 3} б) 3.
7. Тип 13 № 555265 
а) Решите уравнение 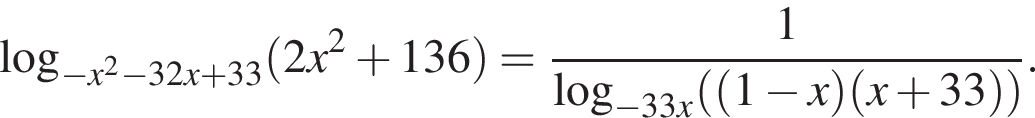
б) Укажите корни этого уравнения, принадлежащие отрезку 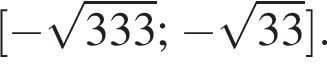
Решение. а) Заметим, что уравнение имеет смысл при 
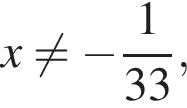
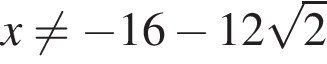 (⁎). Преобразуем его при этих условиях:
(⁎). Преобразуем его при этих условиях:
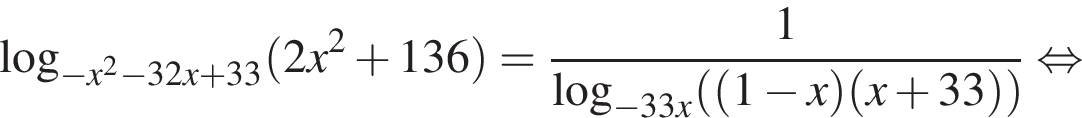
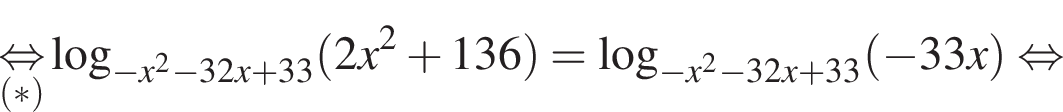
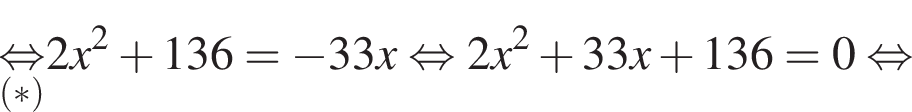
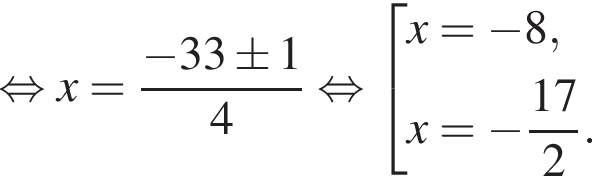
б) Заметим, что 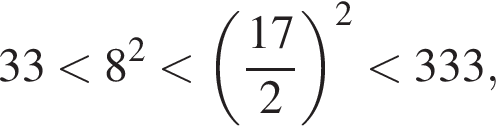 поэтому подходят оба корня.
поэтому подходят оба корня.
Ответ: а) 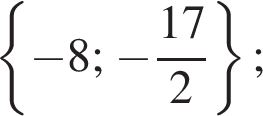 б)
б) 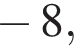
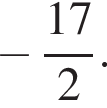
8. Тип 13 № 561853 
а) Решите уравнение 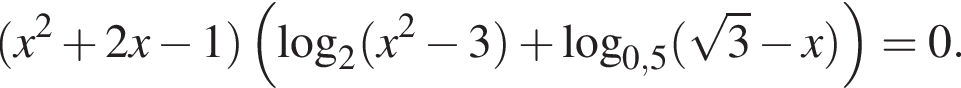
б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
Решение. а) Запишем исходное уравнение в виде:
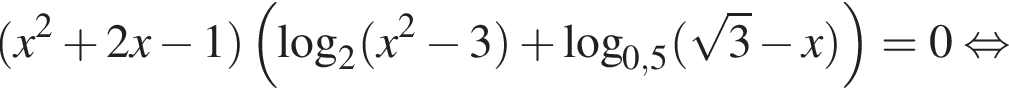
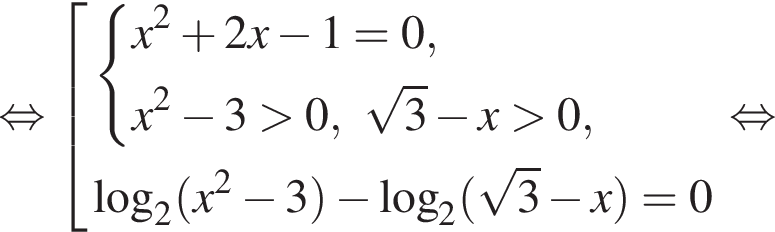
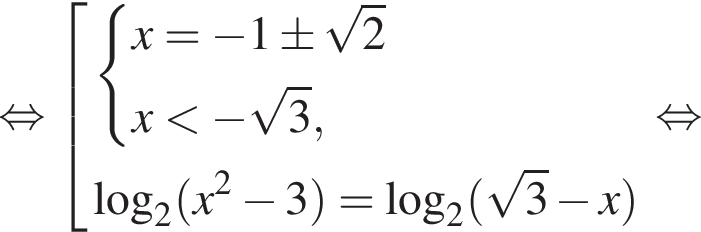
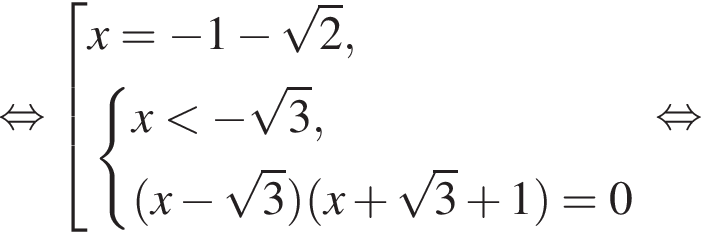
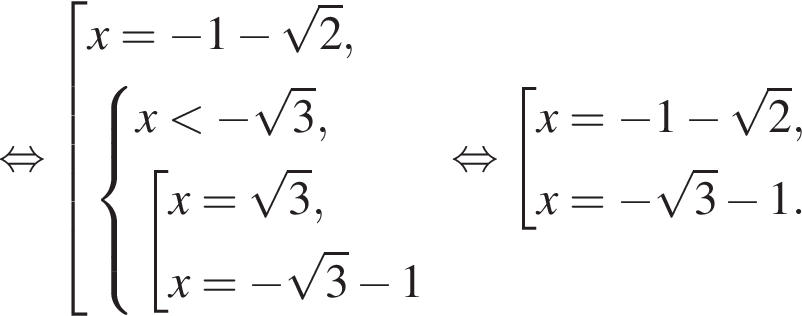
б) Проверим корни на отрезке 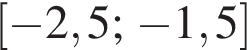 :
:
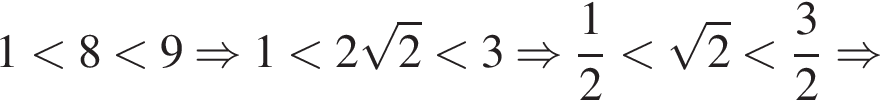

Таким образом, значение 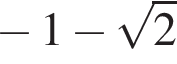 подходит и войдет в ответ.
подходит и войдет в ответ.
Проверим следующее значение x:
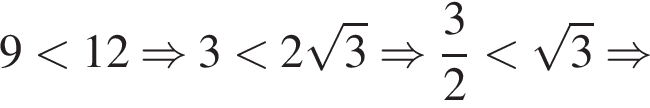
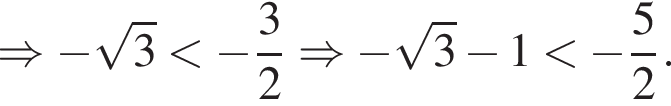
Значит, значение 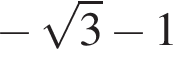 не войдет в ответ.
не войдет в ответ.
Ответ: а) 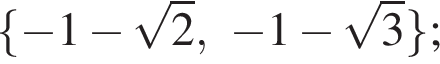 б)
б) 
9. Тип 13 № 643200 
a) Решите уравнение 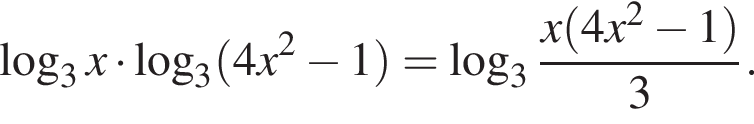
б) Найдите все корни этого уравнения, принадлежащие отрезку 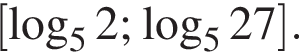
Решение. а) Уравнение имеет вид
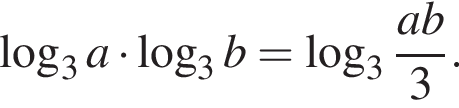
Преобразуем его:
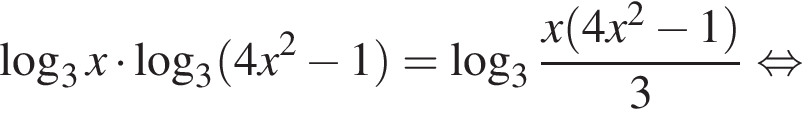
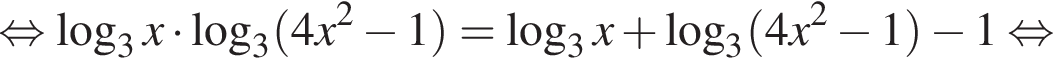
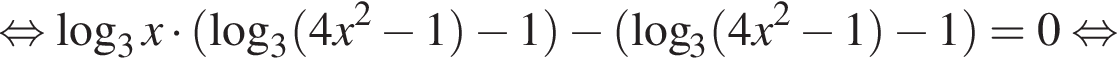
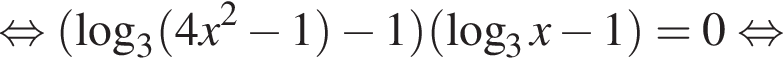
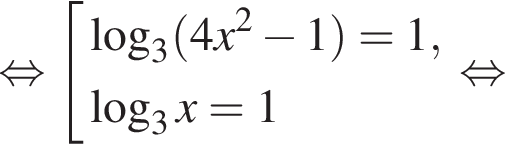
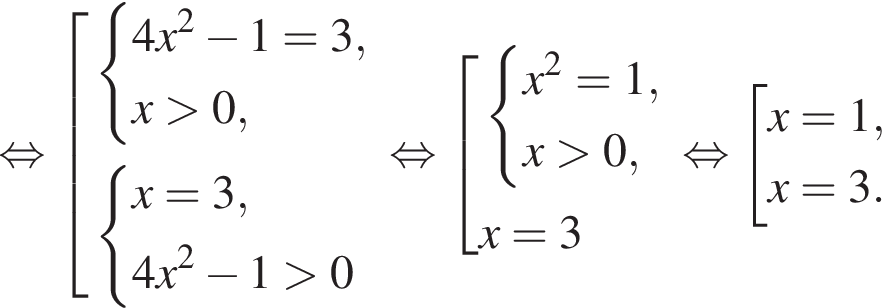
б) Отберём корни этого уравнения, принадлежащие отрезку 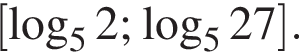 Заметим, что
Заметим, что 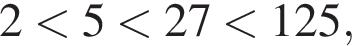 тогда
тогда
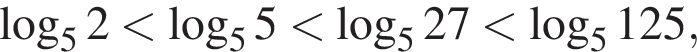
следовательно, 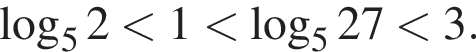 Значит, отрезку
Значит, отрезку 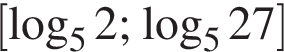 принадлежит только корень
принадлежит только корень 
Ответ: a) 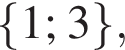 б)
б) 
10. Тип 13 № 643677 
a) Решите уравнение 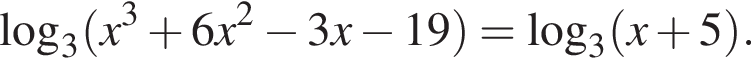
б) Укажите корни этого уравнения, принадлежащие отрезку 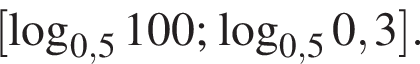
Решение. а) Преобразуем уравнение
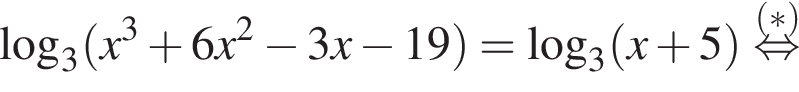
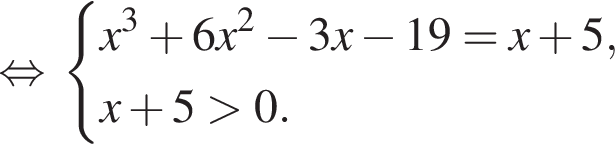
Решим отдельно уравнение полученной системы:


Значит, возвращаясь к системе, получаем
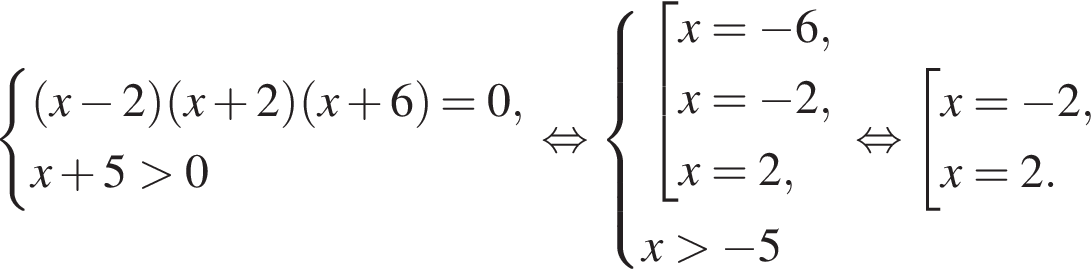
б) Заметим, что
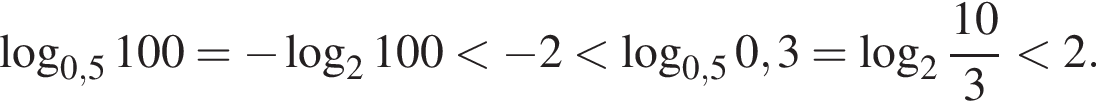
Значит, отрезку 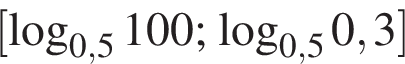 принадлежит корень −2.
принадлежит корень −2.
Ответ: а) {−2; 2}; б) –2.
Самостоятельная работа
Фамилия, Имя______________________________________
1 варант
| Задания | Ответ |
| 1. Найдите значение выражения 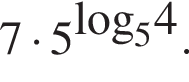
| 28 |
| 2. Найдите корень уравнения 
| -124 |
| 3. Найдите корень уравнения 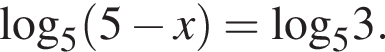
| 2 |
| 4. а) Решите уравнение 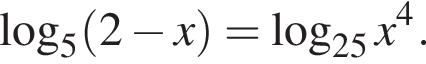 Решение. а) Запишем исходное уравнение в виде: 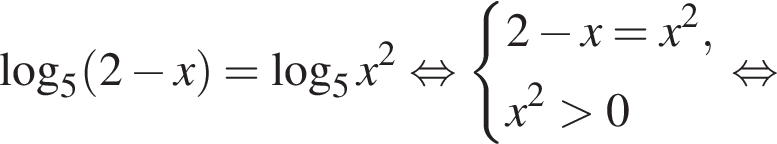 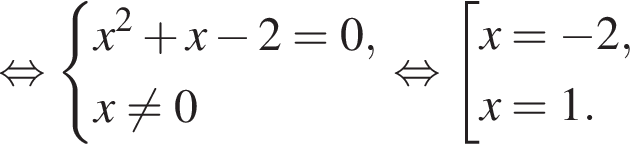 б) Поскольку 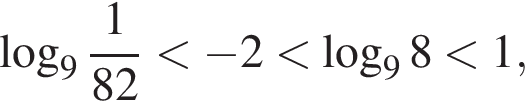 отрезку отрезку 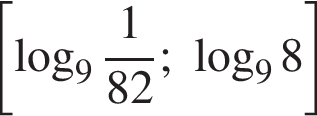 принадлежит единственный корень −2. принадлежит единственный корень −2. б) Укажите корни этого уравнения, принадлежащие отрезку 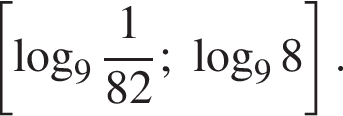
| а) −2; 1, б) −2.
|
Фамилия, Имя______________________________________
2 варант
| Задания | Ответ |
Найдите значение выражения 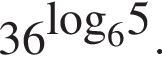
| 25 |
Найдите корень уравнения 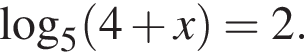
| 21 |
Найдите корень уравнения 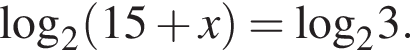
| -12 |
| а) Решите уравнение 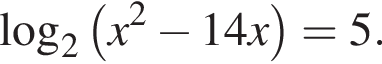 Решение. а) Из уравнения получаем: 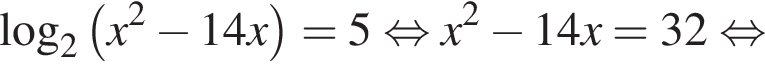 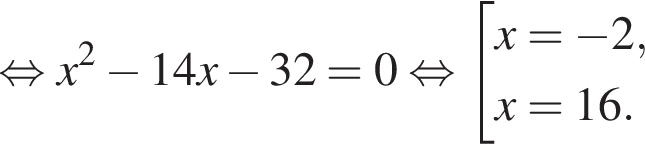 б) Заметим, что 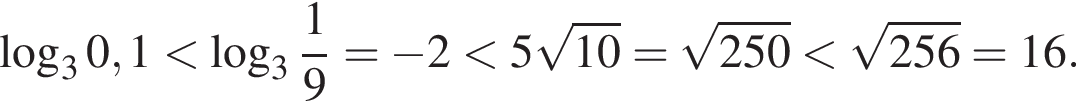 Значит, указанному отрезку принадлежит только корень −2. Значит, указанному отрезку принадлежит только корень −2. б) Укажите корни этого уравнения, принадлежащие отрезку 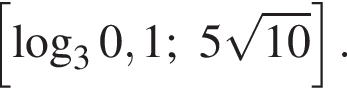
| а) −2 и 16; б) −2. |
Объявить оценки за работу на уроке.
Рефлексия
Задайте формулой любую логарифмическую функцию и запишите на листочке одним из следующих цветов, которые на ваш взгляд соответствуют вашему настроению от проделанной вами работы
Красный – отличное
Зеленый – хорошее
Синий – удовлетворительное.
1. Вычислить устно
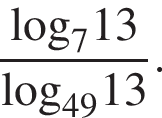
Решение уравнений 1 часть
1.Найдите корень уравнения 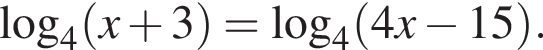
2.Найдите корень уравнения 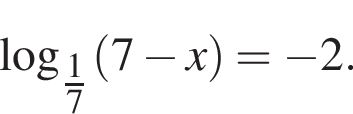
3.Найдите корень уравнения 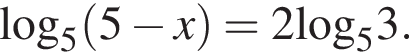
4.Решите уравнение 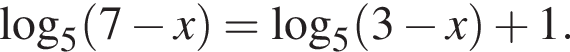
5.Решите уравнение 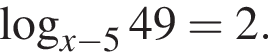 Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
6.Найдите корень уравнения 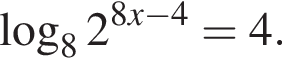
7.Найдите корень уравнения 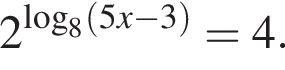
2 часть
1.а) Решите уравнение 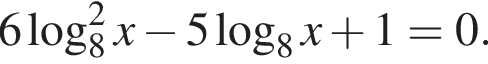
б) Найдите все корни этого уравнения, принадлежащие отрезку 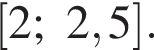







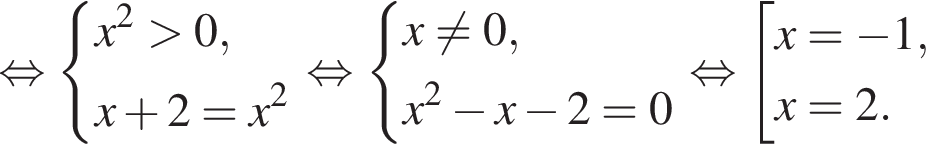
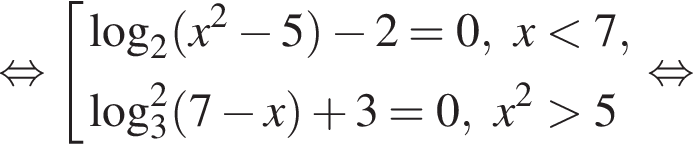
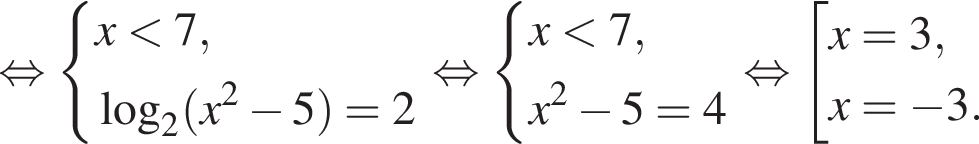
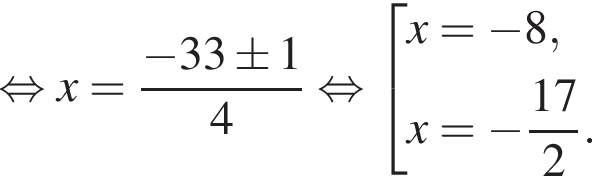
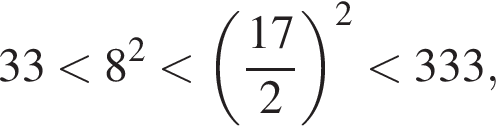 поэтому подходят оба корня.
поэтому подходят оба корня.