Планиметрия в заданиях ОГЭ и ЕГЭ

Планиметрия в заданиях ОГЭ и ЕГЭ

Пропорциональные отрезки в прямоугольном треугольнике

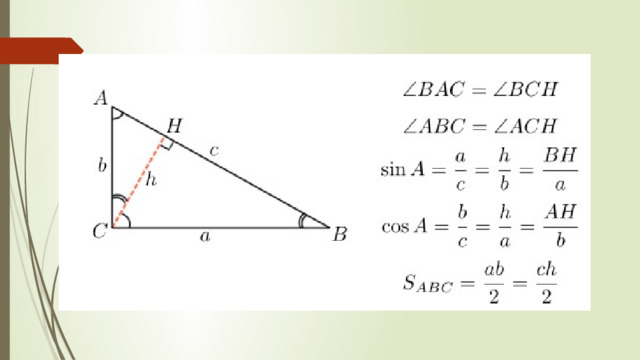
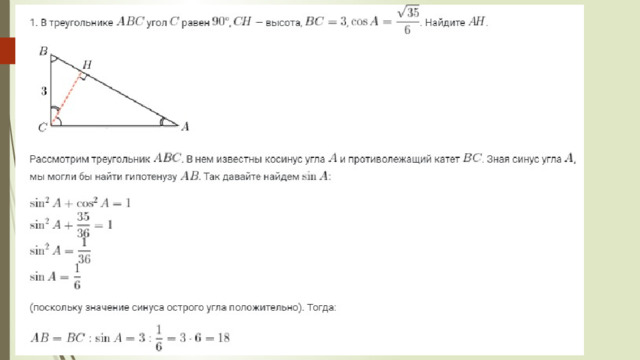
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника , каждый из которых подобен данному треугольнику.

В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

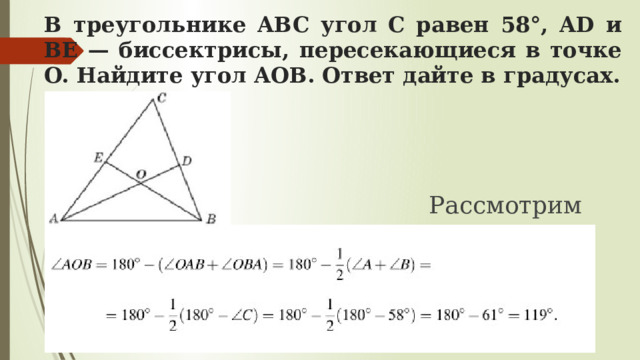
В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.

Решение:

Рассмотрим угол  AOB  

в треугольнике  AOB :

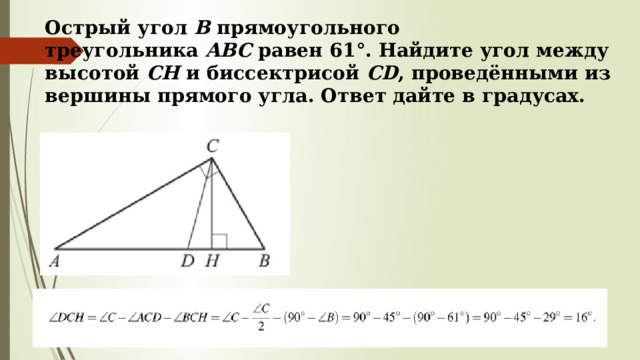
Острый угол  B  прямоугольного треугольника  ABC  равен 61°. Найдите угол между высотой  CH  и биссектрисой  CD , проведёнными из вершины прямого угла. Ответ дайте в градусах.

Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Так как  CM  — медиана, то  AM = MC   (свойство

медианы в прямоугольном треугольнике),

а значит, углы  A  и  ACM  равны как углы при

сновании равнобедренного треугольника.

Заметим, что основание высоты ближе к

вершине большего острого угла.

Имеем:

Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Так как  CM  — медиана, то  AM = MC  (свойство

медианы в прямоугольном треугольнике),

а значит, углы  A  и  ACM  равны как углы при

основании равнобедренного треугольника.

Площадь треугольника.

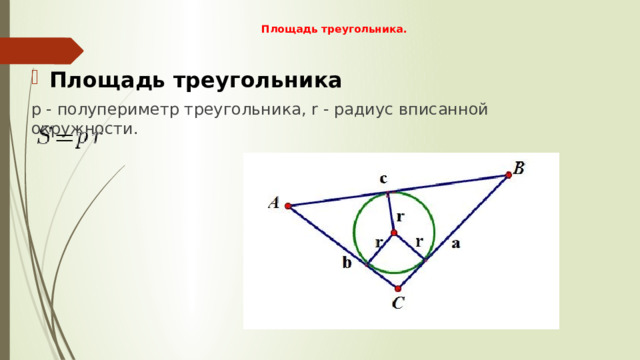
• Площадь треугольника

p - полупериметр треугольника, r - радиус вписанной окружности.

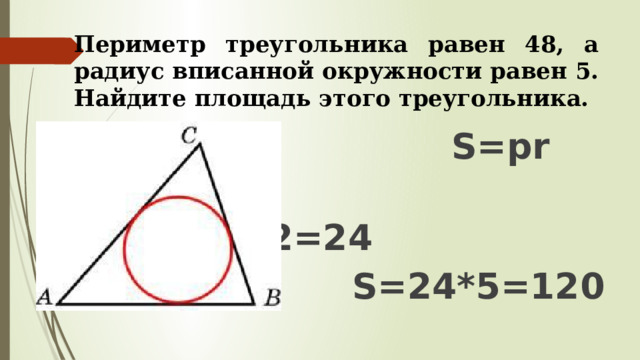
Периметр треугольника равен 48, а радиус вписанной окружности равен 5. Найдите площадь этого треугольника.

S=pr

p=P:2=48:2=24

S=24*5=120

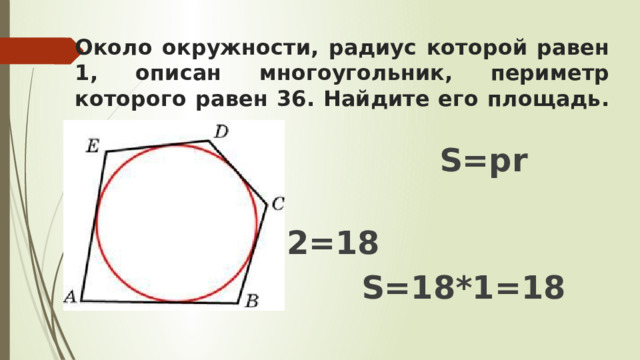
Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 36. Найдите его площадь.

S=pr

p=P:2=36:2=18

S=18*1=18

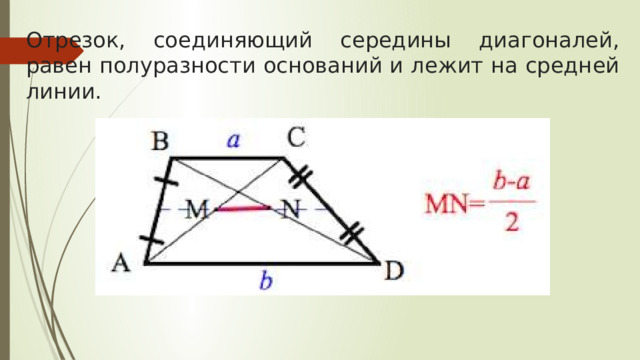
Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

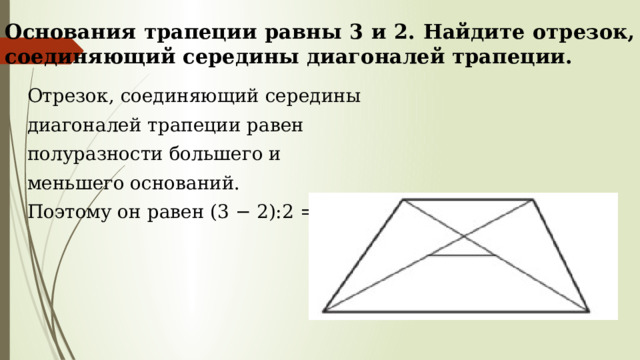
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Отрезок, соединяющий середины

диагоналей трапеции равен

полуразности большего и

меньшего оснований.

Поэтому он равен (3 − 2):2 = 0,5 .

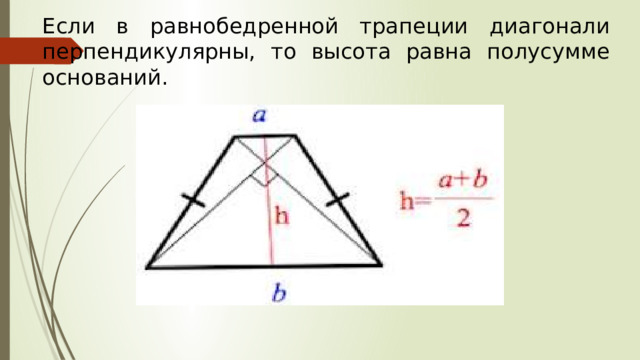
Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

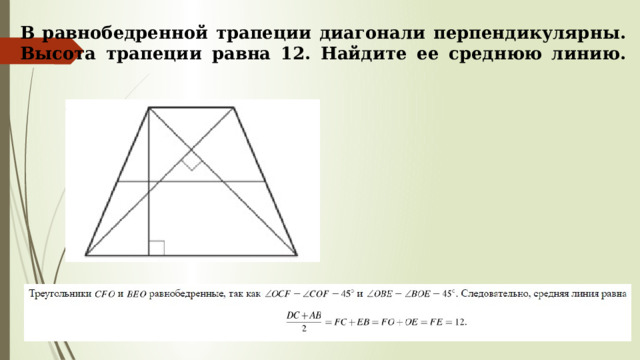
В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

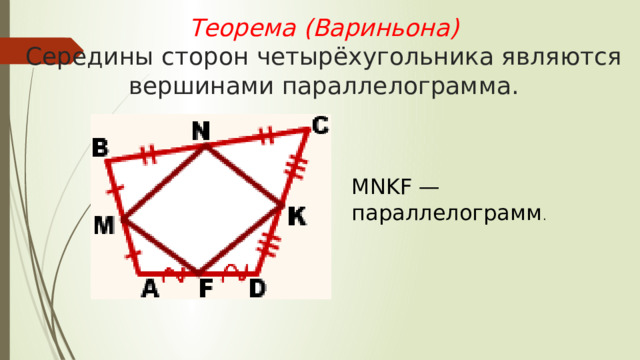
Теорема (Вариньона) Середины сторон четырёхугольника являются вершинами параллелограмма.

MNKF — параллелограмм .

Следствия из теоремы Вариньона

• Периметр параллелограмма Вариньона равен сумме диагоналей исходного параллелограмма

• Площадь параллелограмма Вариньона равна половине площади исходного параллелограмма

Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Стороны искомого четырехугольника равны

средним линиям треугольников,

образуемых диагоналями и сторонами

данного четырехугольника.

Таким образом, стороны искомого

четырехугольника равны половинам диагоналей.

Соответственно,

Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A'B'C'D', вершинами которого являются середины сторон данного параллелограмма.

Четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом, площадь которого равна половине площади исходного четырехугольника (см.  параллелограмм Вариньона ).

Поэтому его площадь равна 76,5.

Ответ:76,5.

• Медиана, проведенная из вершины прямого угла, равна половине гипотенузы. Ее основание является центром описанной около прямоугольного треугольника окружности. Радиус описанной окружности равен этой медиане и равен половине гипотенузы:

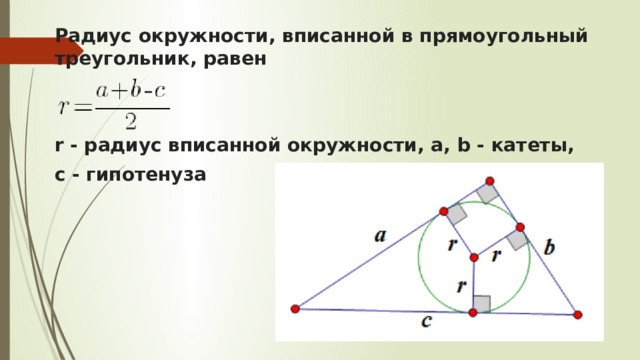
Радиус окружности, вписанной в прямоугольный треугольник, равен

r - радиус вписанной окружности, a, b - катеты,

c - гипотенуза

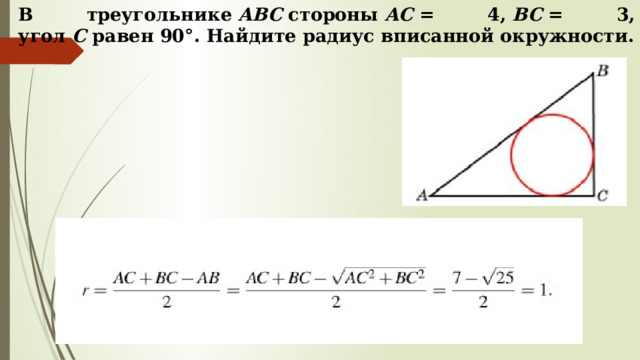
В треугольнике  ABC  стороны  AC  = 4,  BC  = 3, угол  C  равен 90°. Найдите радиус вписанной окружности.