Тема: Площади поверхности многогранников.
Прочитать в предыдущих работах определение прямой призмы, правильной призмы, правильной пирамиды, определения полной и боковой поверхности многогранников.
1). Записать в тетради теоретическую часть:
1. Прямая призма. Начертить треугольную прямую призму .
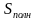 =
= 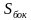 +2•
+2• ,
, 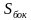 =р• Н = (a +b + .....+c) •Н ,
=р• Н = (a +b + .....+c) •Н ,
где , р - периметр основания призмы, a,b, ... , c - рёбра основания призмы, Н - высота прямой призмы (для прямой призмы высота и боковое ребро совпадают).
(На чертеже подписать a,b, c , Н)
 (площадь основания - то, на чём призма стоит) находится как площадь геометрической фигуры, находящейся в основании (треугольник, прямоугольник, квадрат, трапеция, параллелограмм, ромб, пятиугольник. шестиугольник и т.д.).
(площадь основания - то, на чём призма стоит) находится как площадь геометрической фигуры, находящейся в основании (треугольник, прямоугольник, квадрат, трапеция, параллелограмм, ромб, пятиугольник. шестиугольник и т.д.).
2. Пирамида. Начертить любую пирамиду.
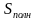 =
= 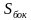 +
+ ,
,
 (то, на чём пирамида стоит) находится как площадь геометрической фигуры, находящейся в основании (треугольник, прямоугольник, квадрат, трапеция, параллелограмм, ромб, пятиугольник, шестиугольник и т.д.)
(то, на чём пирамида стоит) находится как площадь геометрической фигуры, находящейся в основании (треугольник, прямоугольник, квадрат, трапеция, параллелограмм, ромб, пятиугольник, шестиугольник и т.д.)
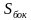 находится как сумма площадей боковых граней(треугольников).
находится как сумма площадей боковых граней(треугольников).
3. Правильная пирамида.
Записать определение апофемы: см чертёж (не путать с высотой самой пирамиды).
Выполнить чертёж.
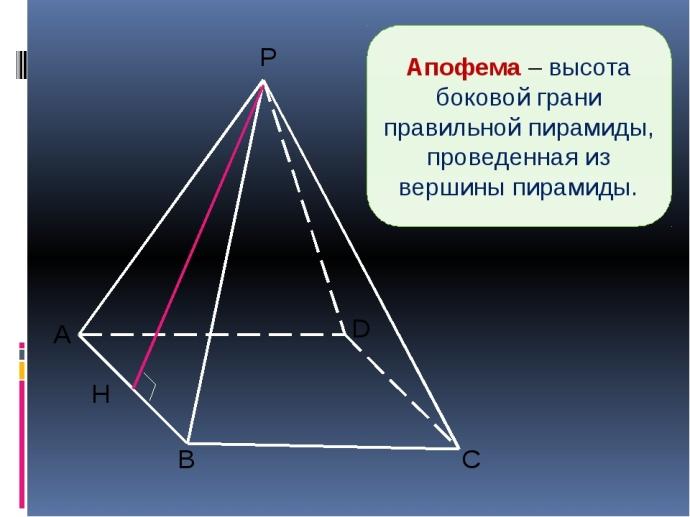
выписать: РН - апофема правильной пирамиды.
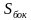 =
= 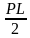 , где P периметр основания, L - апофема.
, где P периметр основания, L - апофема.
(Р= АВ+ВС+CD+AD , L=РН)
4. Формулы площади многоугольников (для нахождения площади основания призмы и пирамиды  )
)
 , где а - сторона треугольника.
, где а - сторона треугольника.
Площадь квадрата:
S=a², где а - сторона квадрата.
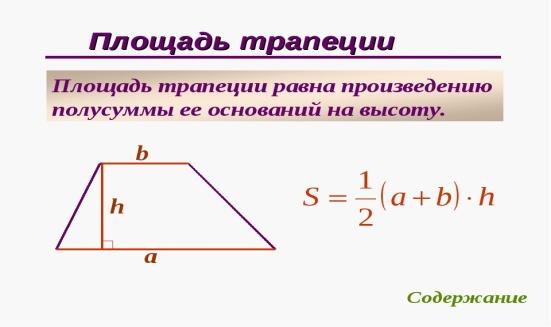
(высоту трапеции не путать с высотой призмы или апофемой пирамиды).
2). Решить задачи (задачи общие, данные взять для своего варианта)
Чертежи обязательно. На чертёж нанести данные. Формулы использовать из конспекта. Формулы в решении записывать.
1. Найти полную поверхность правильной треугольной призмы, если ребро основания призмы равно а см, а боковое ребро равно в см. (ответ будет содержать корень, слагаемые с корнем и без корня не складывать).
2. Найти полную поверхность правильной четырёхугольной пирамиды, если ребро основания равно а м, а апофема равна в м.
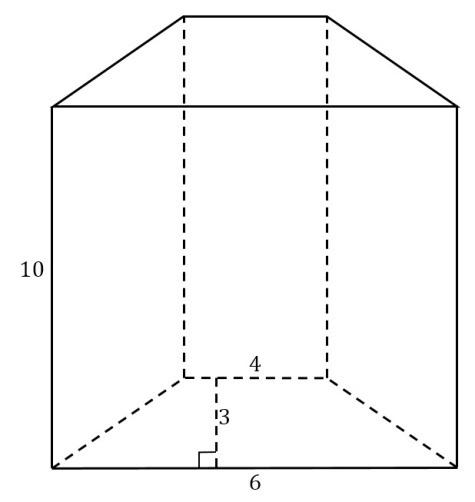
3.Подарочная коробка имеет вид прямой призмы, в основании которой находиться равнобокая трапеция. Сколько упаковочной бумаги потребуется, чтобы оклеить данную коробку? (см. чертёж, размеры даны для примера: H - боковое ребро (высота) призмы равно 10 см, h -высота трапеции (не путать с высотой призмы) равна 3 см, основания трапеции а=4 см и в=6 см).(кроме формул боковой и полной поверхности применить теорему Пифагора для нахождения длин боковых сторон трапеции)
|
| Задача 1 | Задача 2 | Задача 3 |
| 1 | а=4 в=10 | а=3 в=7 | H=50 h=15 а=16 в=24 |
| 2 | а=8 в=10 | а=5 в=9 | H=80 h=30 а=18 в=32 |
| 3 | а=6 в=12 | а=4 в=11 | H=56 h=18 а=17 в=25 |
| 4 | а=2 в=9 | а=6 в=13 | H=90 h=40 а=25 в=35 |
| 5 | а=2 в=8 | а=5 в=8 | H=64 h=32 а=20 в=24 |
| 6 | а=4 в=6 | а=3 в=6 | H=56 h=20 а=18 в=30 |
| 7 | а=6 в=10 | а=5 в=11 | H=70 h=30 а=20 в=34 |
| 8 | а=8 в=11 | а=3 в=8 | H=64 h=30 а=30 в=40 |
| 9 | а=4 в=9 | а=5 в=10 | H=58 h=24 а=22 в=36 |
| 10 | а=6 в=10 | а=4 в=8 | H=78 h=32 а=30 в=44 |







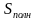 =
= 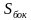 +2•
+2• ,
, 
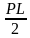 , где P периметр основания, L - апофема.
, где P периметр основания, L - апофема. , где а - сторона треугольника.
, где а - сторона треугольника.





















