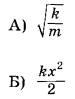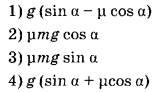Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФОРМУЛЫ 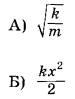
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) амплитуда колебаний скорости 2) циклическая частота колебаний 3) максимальная кинетическая энергия груза 4) период колебаний |
Решение.
А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле 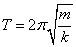 , а частота как
, а частота как 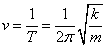 . Циклическая частота
. Циклическая частота 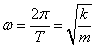 , следовательно, для буквы А имеем ответ под номером 2.
, следовательно, для буквы А имеем ответ под номером 2.
Б) Для пружинного маятника известны формулы кинетической энергии 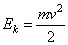 и потенциальной энергии
и потенциальной энергии 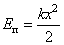 . Учитывая, что начальная скорость тела равна 0, то вся потенциальная энергия переходит в кинетическую, то есть
. Учитывая, что начальная скорость тела равна 0, то вся потенциальная энергия переходит в кинетическую, то есть 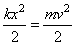 . Ответ под номером 3.
. Ответ под номером 3.
Ответ: 23.
Задание 7. После удара шайба массой m начала скользить с начальной скоростью v0 вверх по плоскости, установленной под углом а к горизонту (см. рисунок). Переместившись вдоль оси Ох на расстояние s, шайба соскользнула в исходное положение. Коэффициент трения шайбы о плоскость равен µ. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих движение шайбы.
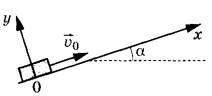
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
| ФОРМУЛЫ 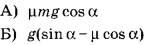
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) модуль ускорения шайбы при её движении вверх 2) модуль проекции силы тяжести на ось Ох 3) модуль силы трения 4) модуль ускорения шайбы при её движении вниз |
Решение.
На рисунке ниже показаны силы, действующие на тело, при его движении по наклонной плоскости.
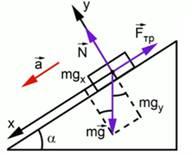
Сила, действующая на тело, складывается из трех сил: силы тяжести, силы реакции опоры и силы трения. Проекция этих трех сил на ось Ox дает:
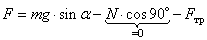 ,
,
Сила трения равна проекции силы тяжести на ось Oy, умноженная на коэффициент трения µ:
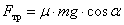 ,
,
и для равнодействующей силы можно записать
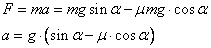
А) Модуль силы трения – ответ 3.
Б) Модуль ускорения шайбы – ответ 4.
Ответ: 34.
Задание 7. После удара шайба массой m начала скользить со скоростью v0 вверх по плоскости, установленной под углом а к горизонту (см. рисунок). Переместившись вдоль оси Ох на некоторое расстояние, шайба соскользнула в исходное положение. Коэффициент трения шайбы о плоскость равен µ.
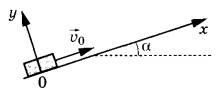
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) модуль ускорения шайбы при её движении вверх Б) модуль силы трения | ФОРМУЛЫ 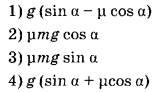
|
Решение.
На рисунке ниже показаны силы, действующие на тело, при его движении по наклонной плоскости.
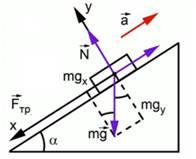
Равнодействующая сила, действующая на тело, движущееся вверх по наклонной плоскости, складывается из трех сил: силы тяжести, силы реакции опоры и силы трения. Проекция этих трех сил на ось Ox дает:
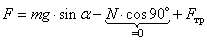 ,
,
Сила трения равна проекции силы тяжести на ось Oy, умноженная на коэффициент трения µ:
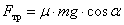 ,
,
и для равнодействующей силы можно записать
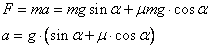
А) Из приведенных ранее выкладок видно, что ускорение равно 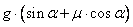 - ответ под номером 4.
- ответ под номером 4.
Б) Модуль силы трения – это 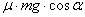 , что соответствует формуле под номером 2.
, что соответствует формуле под номером 2.
Ответ: 42.
Задание 7. Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью v, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен µ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) модуль силы трения, действующей на грузовик Б) тормозной путь грузовика | ФОРМУЛЫ 
|
Решение.
А) Сила трения при торможении грузовика равна 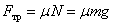 . Это соответствует варианту ответа 1.
. Это соответствует варианту ответа 1.
Б) Грузовик тормозит за счет силы трения, то есть с ускорением
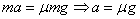
Время торможения до полной остановки можно найти как
 .
.
Тогда тормозной путь будет равен

и подставляя вместо t и a найденные выражения, получаем:
.
Имеем вариант ответа под номером 4.
Ответ: 14.
Задание 7. Груз, привязанный к нити, отклонили от положения равновесия и в момент t=0 отпустили из состояния покоя (см. рисунок). На графиках А и Б показано изменение физических величин, характеризующих движение груза после этого. (Т — период колебаний груза.) Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
| ГРАФИКИ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) координата х 2) проекция скорости vx 3) кинетическая энергия Ек 4) потенциальная энергия Еп |
Решение.
1) Координата x, как видно из рисунка, сначала принимает отрицательное значение, затем проходит через 0, становится положительной, а затем, вновь возвращается в исходную точку и становится отрицательной. Это один период колебания T маятника. Данное описание подходит к рисунку Б.
2) Изначально скорость маятника равна 0. Это не соответствует ни одному из графиков.
3) Кинетическая энергия маятника при t=0 равна 0, так как скорость маятника равна 0. Также не подходит ни для одного графика.
4) Потенциальная энергия при t=0 максимальна, затем, в точке 0 становится равной 0, после этого вновь достигает максимального значения, и все повторяется при обратном ходе маятника. Это соответствует рисунку под буквой А.
Ответ: 41.
Задание 7. В момент t = 0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок). Сопротивлением воздуха пренебречь. Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
| ГРАФИКИ 
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) координата х мячика 2) проекция скорости мячика на ось х 3) проекция ускорения мячика на ось у 4) координата y мячика |
Решение.
1) Проекция координаты x тела, брошенного под углом к горизонту, линейно возрастает со временем. Этому не соответствует ни один из графиков.
2) При движении тела под углом к горизонту его горизонтальная проекция скорости  . Этому соответствует график под буквой Б.
. Этому соответствует график под буквой Б.
3) Ускорение мячика на ось y равно ускорению свободного падения g, сначала с отрицательным знаком, а затем, с положительным.
4) Координата y мячика сначала плавно возрастает, а затем, убывает со все возрастающей скоростью. Этому соответствует график под буквой А.
Ответ: 42.
Задание 7. Тело, брошенное с горизонтальной поверхности Земли со скоростью v под углом α к горизонту, в течение времени t поднимается на максимальную высоту h над горизонтом. Сопротивление воздуха пренебрежимо мало.
Установите соответствие между физическими величинами и формулами, по которым их можно определить.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) время подъёма t на максимальную высоту Б) максимальная высота h над горизонтом | ФОРМУЛЫ |
Решение.
А) На максимальной высоте h начальная вертикальная скорость тела, равная  (ее проекция на ось Oy), полностью компенсируется ускорением свободного падения g, то есть скорость становится равной нулю:
(ее проекция на ось Oy), полностью компенсируется ускорением свободного падения g, то есть скорость становится равной нулю:
 ,
,
откуда время подъема равно
 .
.
Б) Максимальную высоту h можно найти из формулы
 ,
,
где  - начальный уровень по высоте. Подставляя вместо времени его выражение, получаем:
- начальный уровень по высоте. Подставляя вместо времени его выражение, получаем:
.
Ответ: 41.
Задание 7. Установите соответствие между зависимостью проекции скорости тела от времени и зависимостью проекции перемещения этого тела от времени для одного и того же движения (все величины выражены в СИ).
| ПРОЕКЦИЯ СКОРОСТИ | ПРОЕКЦИЯ ПЕРЕМЕЩЕНИЯ |
Решение.
Зная закон изменения скорости, закон изменения перемещения тела находится как первообразная от скорости.
А) Первообразная для скорости будет равна  , что соответствует закону перемещения под номером 4.
, что соответствует закону перемещения под номером 4.
Б) Первообразная от скорости равна  - вариант ответа под номером 1.
- вариант ответа под номером 1.
Ответ: 41.
Задание 7. Два пластилиновых шарика массами 2m и m находятся на горизонтальном гладком столе. Первый из них движется ко второму со скоростью v, а второй покоится относительно стола. Укажите формулы, по которым можно рассчитать модули изменения скоростей шариков в результате их абсолютно неупругого удара. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) модуль изменения скорости первого шарика Б) модуль изменения скорости второго шарика | ФОРМУЛЫ |
Решение.
По закону сохранения импульсов можно записать, что суммарный импульс шариков до удара и после удара равны, то есть
 ,
,
где  - импульс первого шарика до удара;
- импульс первого шарика до удара;  - импульс второго шарика до удара;
- импульс второго шарика до удара;  - импульс обоих шаров после удара. Отсюда находим скорость шариков после удара:
- импульс обоих шаров после удара. Отсюда находим скорость шариков после удара:
 .
.
А) Начальная скорость первого шарика была равна v, следовательно, она изменилась на величину  .
.
Б) Начальная скорость второго шарика была равна 0, поэтому ее изменение равно  .
.
Ответ: 42.
Задание 7. С высоты h по наклонной плоскости из состояния покоя соскальзывает брусок массой m. Длина наклонной плоскости равна S, а коэффициент трения между бруском и плоскостью равен µ. Установите соответствие между физическими величинами и формулами, по которым их можно определить.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) сила трения, действующая на брусок Б) время движения бруска | ФОРМУЛЫ |
Решение.
А) Сила трения, действующая на брусок равна  , где
, где  - сила реакции опоры; α – угол наклона. Косинус угла наклона – это отношение прилежащего катета (длины основания) на гипотенузу (длины S наклонной плоскости ):
- сила реакции опоры; α – угол наклона. Косинус угла наклона – это отношение прилежащего катета (длины основания) на гипотенузу (длины S наклонной плоскости ):
 ,
,
где  по теореме Пифагора. Таким образом, сила трения равна
по теореме Пифагора. Таким образом, сила трения равна
.
Б) Равнодействующая сил, действующая на брусок, равна
 .
.
Синус угла – это отношение противолежащего катета (высоты h) на гипотенузу (длину S), получаем:
.
С этим ускорение тело пройдет путь S за время t:
 ,
,
откуда
.
Ответ: 43.
Задание 7. В момент t = 0 шарик бросили вертикально вверх с начальной скоростью v (см. рисунок). Сопротивление воздуха пренебрежимо мало. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять (t0 — время полёта).

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ 
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) проекция скорости шарика vy 2) проекция ускорения шарика ay 3) координата y шарика 4) модуль силы тяжести, действующей на шарик |
Решение.
1) Скорость vy тела в начальный момент была v0 и постепенно уменьшалась, достигая максимальной высоты. Ни один из графиков не подходит.
2) Проекция ускорения ay шарика сначала была отрицательной (скорость шарика замедлялась), а затем, стала положительной (скорость шарика при падении увеличивалась). Не подходит ни один из графиков.
3) Координата y сначала была равна 0, затем, равнозамедленно увеличилась до максимальной величины, а потом, равноускоренно вновь уменьшилась до нуля. Подходит график А.
4) Модуль силы тяжести равна F=mg – величина постоянная и положительная. Подходит график Б.
Ответ: 34.
Задание 7. Груз, привязанный к нити, в момент t = 0 вышел с начальной скоростью из состояния равновесия (см. рисунок). На графиках А и Б показано изменение физических величин, характеризующих движение груза после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
| ГРАФИКИ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) координата груза х 2) проекция скорости груза vx 3) кинетическая энергия груза Ек 4) потенциальная энергия груза Еп |
Решение.
1) В момент t=0 координата груза x=0, затем, она отклоняется в сторону отрицательных значений с замедлением скорости, достигается своего крайнего правого отклонения, затем вновь возвращается в точку x=0 с возрастающей скоростью. После этого идет отклонение груза влево с теми же скоростями. Этому описанию соответствует график Б.
2) В момент времени t=0 скорость груза максимальна. Ни один из графиков не подходит (оба графика начинаются с нуля).
3) Кинетическая энергия груза в момент времени t=0 принимает максимальное значение. Не подходит ни один из графиков.
4) Потенциальная энергия груза при t=0 равна нулю, затем, постепенно возрастает и в крайнем правом отклонении груза принимает максимальное значение, затем, вновь постепенно уменьшается до нуля (когда x=0), после этого снова увеличивается и при отклонении груза в крайнее левое положение принимает максимальное значение. Этому соответствует график А.
Ответ: 41.
Задание 7. В инерциальной системе отсчёта (ИСО) за время ∆t под действием постоянной силы импульс тела массой m изменился на ∆p.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) сила, действующая на тело Б) ускорение тела в ИСО | ФОРМУЛЫ |
Решение.
А)-Б) Изменение импульса происходит вследствие изменение скорости, то есть  . В свою очередь изменение скорости за время ∆t равно
. В свою очередь изменение скорости за время ∆t равно  , где a – ускорение тела. Ускорение телу придает сила F=ma. Выразим ускорение через изменение импульса, получим:
, где a – ускорение тела. Ускорение телу придает сила F=ma. Выразим ускорение через изменение импульса, получим:

и сила F равна
 .
.
Ответ: 23.
Задание 7. Шайба массой m съезжает с горки без трения из состояния покоя. Ускорение свободного падения равно g. У подножия горки кинетическая энергия шайбы равна Ек. Чему равны высота горки и модуль импульса шайбы у подножия горки? Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
| ФИЗИЧЕСКАЯ ВЕЛИЧИНА А) высота горки Б) модуль импульса шайбы у подножия горки | ФОРМУЛА |
Решение.
А) Так как шайба движется без трения, то вся начальная потенциальная энергия шайбы в начале движения E=mgh (где h – высота горки) переходит в кинетическую энергию Eк:
 ,
,
откуда
 .
.
Б) Импульс шайбы у подножия горки равен p=mv, где v – скорость шайбы у подножия. Скорость шайбы можно найти из выражения кинетической энергии
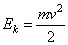 ,
,
откуда скорость

и модуль импульса шайбы равен
.
Ответ: 42.
Задание 7. Материальная точка движется по оси х. Её координата меняется по закону: x(t)=Asin(wt+φ0).
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) амплитуда скорости точки Б) амплитуда ускорения точки | ФОРМУЛЫ |
Решение.
А) Закон скорости точки можно получить путем вычисления производной x(t) по времени t, получим:
 ,
,
откуда амплитуда скорости равна  .
.
Б) Закон ускорения точки – это производная скорости v(t) по времени t:
и амплитуда ускорения равна  .
.
Ответ: 34.