Подготовка к базовой форме ЕГЭ. Задание 20.

Базовая форма ЕГЭ

Задание №20.

ПРИМЕР ЗАДАЧИ 1: На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 50 км, между А и В — 40 км, между В и Г — 25 км, между Г и А — 35 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.

РЕШЕНИЕ: Данную задачу проще всего решать графически. Рассмотрим всевозможные варианты расположения бензоколонок по кольцевой дороге, но перед этим посчитаем количество различных вариантов (начиная с точки А по часовой стрелке): АВГБ и АБГВ АГБВ и АВБГ АБВГ и АГВБ.

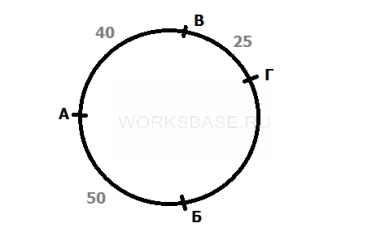
Всего разных вариантов получается 3, рассмотрим каждый из них.

В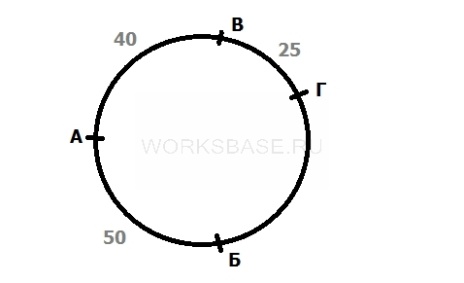 ариант 1. Отмечаем местоположение бензоколонки А. Бензоколонку Б расположим на расстоянии 50 км против часовой стрелки относительно А. Бензоколонку В – на расстоянии 40 км по часовой стрелке относительно А. Бензоколонку Г – на расстоянии 25 км по часовой стрелке относительно В. Тогда расстояние от А до Г равно 65 км (40 + 25 через В) или более 50 км (через Б), а оно должно быть равно 35. Значит, данный вариант не подходит.

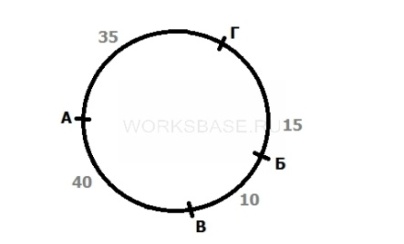Вариант 2. Отмечаем местоположение бензоколонки А. Бензоколонку Б расположим на расстоянии 50 км против часовой стрелки относительно А. Бензоколонку В – на расстоянии 40 км против часовой стрелки относительно А. Бензоколонку Г – на расстоянии 25 км против часовой стрелки относительно В. Тогда расстояние от А до Г через В и Б равно 65 км, а по часовой стрелке оно вполне может быть равно 35 км. В этом случае расстояние между Б и В равно 10 км.

Вариант 3. Отмечаем местоположение бензоколонки А. Бензоколонку Б расположим на расстоянии 50 км против часовой стрелки относительно А. Бензоколонку В – на расстоянии 40 км против часовой стрелки относительно А. Бензоколонку Г – на расстоянии 25 км по часовой стрелке относительно В. Тогда расстояние от А до Г по кратчайшей дуге равно 15 км, а оно должно быть равно 35 км. Значит, данный вариант не подходит. Все остальные варианты будут совпадать с предыдущими.

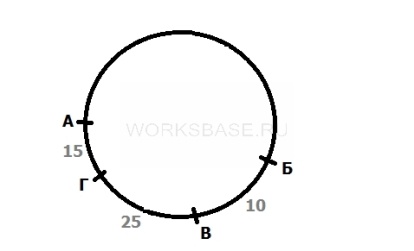
Получается, что расстояние между бензоколонками Б и В равно 10 км.

ОТВЕТ: 10 

ПРИМЕР ЗАДАЧИ 2: Саша пригласил Петю в гости, сказав, что живёт в десятом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)

РЕШЕНИЕ: Для удобства обозначим буквой A количество квартир на этаже. Тогда в любом подъезде количество квартир равно: A ⋅ 9

Теперь вычислим номер первой и последней квартиры в десятом подъезде, чтобы получить диапазон, в котором находится квартира Саши: A ⋅ 9 ⋅ 9 + 1 — номер первой квартиры в десятом подъезде.

A ⋅ 9 ⋅ 10 — номер последней квартиры в десятом подъезде.

A ⋅ 9 ⋅ 9 + 1 ≤ 333 ≤ A ⋅ 9 ⋅ 10.

Из этого неравенства можно вычислить количество квартир на этаже: 81 ⋅ A + 1 ≤ 333 90 ⋅ A ≥ 333 81 ⋅ A ≤ 332 90 ⋅ A ≥ 333 A ≤ 4,1 A ≥ 3,7.

Единственное целое число из диапазона равно 4. Значит, на каждом этаже находится ровно 4 квартиры.

Теперь можно вычислить номер первой квартиры в 10 подъезде: 4 ⋅ 9 ⋅ 9 + 1 = 325 Первая квартира в 10 подъезде находится на первом этаже.

Вычислим, на каком этаже живет Саша: 1 этаж: 325, 326, 327, 328 2 этаж: 329, 330, 331, 332 3 этаж: 333, ... Таким образом, квартира Саши находится на 3 этаже.

ОТВЕТ: 3

ПРИМЕР ЗАДАЧИ 3: Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.

РЕШЕНИЕ: Для удобства дадим название каждой стороне прямоугольника (см. рисунок).

И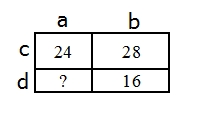 распишем, чему равен периметр каждого маленького прямоугольника по часовой стрелке: P1 = 2a + 2c = 24, P2 = 2b + 2c = 28, P3 = 2b + 2d = 16, P4 = 2a + 2d = ?

Выразим стороны a и d из первого и третьего периметра и подставим их в периметр четвертого прямоугольника: 2a = 24 – 2c 2d = 16 – 2b P4 = 24 – 2c + 16 – 2b

Мы также можем выразить сторону b через второй периметр, чтобы периметр четвертого прямоугольника был выражен только через одну сторону: 2b = 28 – 2c P4 = 24 – 2c + 16 – (28 – 2c) = 24 – 2c + 16 – 28 + 2c = 24 + 16 – 28 = 12

В результате все неизвестные сократились и был найден периметр четверного прямоугольника, равный 12.

ОТВЕТ: 12

В общем виде решение данной задачи на смекалку выглядит следующим образом: ПЕРИМЕТР ПРЯМОУГОЛЬНИКА = A + C – B где A , B и C – периметры трех других прямоугольников, начиная с левого верхнего и далее по часовой стрелке. Осталось лишь подставить все значения и получить ответ.

ПРИМЕР ЗАДАЧИ 4: Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 12, 18 и 30. Найдите площадь четвёртого прямоугольника.

РЕШЕНИЕ: Для удобства дадим название каждой стороне прямоугольника (см. рисунок).

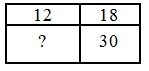
И распишем, чему равна площадь каждого маленького прямоугольника по часовой стрелке: S1 = a ⋅ c = 12 S2 = b ⋅ c = 18 S3 = b ⋅ d = 30 S4 = a ⋅ d = ?

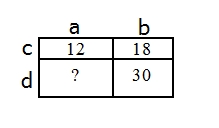
Выразим стороны a и d из первой и третьей площади и подставим их в площадь четвертого прямоугольника: a = 12 / c d = 30 / b S4 = 12 / c ⋅ 30 / b

Мы также можем выразить сторону b через вторую площадь, чтобы площадь четвертого прямоугольника была выражена только через одну сторону: b = 18 / c S4 = 12 / c ⋅ 30 / 18 ⋅ c = 12 ⋅ 30 / 18 = 20

В результате все неизвестные сократились и была найдена площадь четверного прямоугольника, равная 20.

ОТВЕТ: 20

ПРИМЕР ЗАДАЧИ 5. Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?

РЕШЕНИЕ: Пусть x – это количество верных ответов ученика, а y – количество неверных ответов ученика.

Тогда количество отсутствующих ответов равно: 33 – x – y

Запишем все известные условия в виде системы: 7x – 12y = 70 x + y ≤ 33 y ≥ 1

Ученик набрал 70 очков за викторину, значит он дал больше правильных ответов, чем неправильных.

Поэтому попробуем подобрать такое целое y (так как оно меньше x), чтобы число x также было целым: y = 1: 7x – 12 = 70; 7x = 82; x ≈ 11,7 – не целое

y = 2: 7x – 24 = 70; 7x = 94; x ≈ 13,4 – не целое

y = 3: 7x – 36 = 70; 7x = 106; x ≈ 15,1 – не целое

y = 4: 7x – 48 = 70; 7x = 118; x ≈ 16,8 – не целое

y = 5: 7x – 60 = 70; 7x = 130; x ≈ 18,6 – не целое

y = 6: 7x – 72 = 70; 7x = 142; x ≈ 20,3 – не целое

y = 7: 7x – 84 = 70; 7x = 154; x = 22

Получается, что количество правильных ответов равно 22. В сумме с 7 получается 29 (

ОТВЕТ: 22

ПРИМЕР ЗАДАЧИ 6: В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором — 97, в третьем — 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице?

РЕШЕНИЕ: Вычислим сумму натуральных чисел во всей таблице, для этого нужно сложить суммы чисел во всех столбцах: 103 + 97 + 93 = 293

Теперь найдем диапазон, в котором лежит число строк таблицы. Для этого разделим сумму чисел в таблице на сумму чисел в строке. Поскольку сумма чисел в строке больше 21, но меньше 24, она может быть равна 22 или 23.

Если сумма в строке равна 22, то: 293 / 22 ≈ 13,3 Если сумма чисел в строке равна 23, то: 293 / 23 ≈ 12,7 Получается, что число строк в таблице лежит в диапазоне от 12,7 и 13,3.

Единственное целое число, лежащее в данном диапазоне, равно 13.

ОТВЕТ: 13

В общем виде решение данной задачи на смекалку выглядит следующим образом: (A + B + C) / N

ПРИМЕР ЗАДАЧИ 7. В классе учится 25 учащихся. Несколько из них ходили в кино, 18 человек ходили в театр, причём и в кино, и в театр ходили 12 человек. Известно, что трое не ходили ни в кино, ни в театр. Сколько человек из класса ходили в кино?

РЕШЕНИЕ: Для удобства изобразим решение с помощью кругов Эйлера.

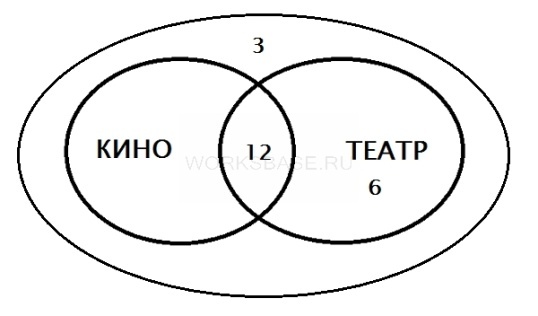
Один круг содержит всех учащихся, которые ходили в кино. Другой круг – всех учащихся, которые ходили в театр. Они пересекаются, так как есть учащиеся, которые были и в кино и в театре. Также есть общий круг, содержащий всех учащихся класса. Распределим известные данные по картинке. И в кино и в театр ходили 12 человек, поэтому 12 вписываем на пересечении кругов. 3 человека не ходили ни в кино, ни в театр, поэтому вписываем их за пределами кругов кино и театра. В театр ходили 18 человек. 12 из них уже указаны, поэтому осталось 6 человек, которые были только в театре. Чтобы узнать, сколько человек были только в кино, нужно из общего числа человек вычесть всех остальных: 25 – 3 – 12 – 6 = 4.

Добавим это число на картинку:

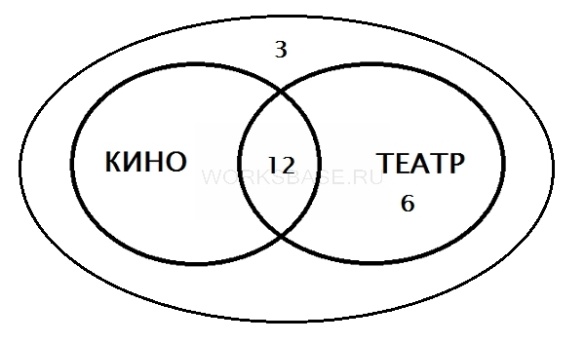
Осталось лишь посчитать, сколько человек были в кино. Для этого нужно сложить учащихся, которые были только в кино, и тех, кто были и в кино и в театре: 4 + 12 = 16 Таким образом, в кино было всего 16 учащихся.

ОТВЕТ: 16

Источник: http://worksbase.ru/matematika/kak-reshat/114-spisok-zadanii-viktoriny.html

Задачи для самостоятельного решения. (ОБЗ)

1. На кольцевой дороге расположено 4 бензоколонки А, Б, В, Г. Расстояние между А и Б равно 55 км, между А и В равно 50 км, между В и Г равно 40 км, между Г и А равно 20 км. Найдите расстояние между Б и В. 2. На кольцевой дороге расположены четыре бензоколонки А и Б - 75км, между А и В - 50 км, между В и Г - 40км, между Г и А - 60км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние в километрах между Б и В. 3. Саша пригласил Петю в гости сказав что живет в седьмом подъезде в квартире №462 а этаж сказать забыл. Подойдя к дому Петя обнаружил что дом семиэтажный. На каком этаже живет Саша?

4.  Саша пригласил Петю в гости, сказав, что живёт в восьмом подъезде в квартире № 468, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом двенадцатиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)

5. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника. 6. Прямоугольник разбит на четыре маленьких прямо- угольника двумя прямолинейными разрезами. Площади трёх из них начиная с левого верхнего и далее по часовой стрелке равны 12, 15 и 30. Найдите площадь четвёртого прямоугольника. 7. Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трех из них, начиная с левого верхнего и далее по часовой
стрелке, равны 18, 15, 20. Найдите площадь четвертого прямоугольника. 8. Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них начиная с левого верхнего и далее по часовой стрелке равны 18, 12 и 20. Найдите площадь четвёртого прямоугольника. 9. Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 84 очка, если известно, что по крайней мере один раз он ошибся? 10. Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный у него списывали 9 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 56 очков, если известно, что по крайней мере один раз он ошибался? 11. В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 119, во втором - 125, в третьем - 133, а сумма чисел в каждой строке больше 15, но меньше 18. Сколько всего строк в столбце? 
12. В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 85, во втором — 77, в третьем — 71, а сумма чисел в каждой строке больше 12, но меньше 15. Сколько всего строк в таблице?

13. В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, в кино и в музей - 6 человек, а 2 человека не ходили ни в кино, ни в музей. Сколько человек нашего класса ходили в кино?

14. В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, в кино 21 человек,5 человек не ходили ни на экскурсию ни в кино. Сколько человек ходили и на экскурсию и в кино?

Ответы:1)5; 2)25; 3)5; 4)10; 5) 12; 6) 24; 7) 24; 8) 30; 9) 23; 10) 17; 11) 23; 12) 17; 13) 11; 14) 19.

Источник: http://mathege.ru/

5