Подготовка к ЕГЭ

11 класс

Площадь боковой и полной поверхностей конуса

Площадь полной поверхности конуса равна 35. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 3:2, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

  Отсеченный и исходный конус подобны с коэффициентом подобия 3/5. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия. Поэтому площади поверхностей отсеченного конуса и исходного конуса относятся как 9/25. Тогда площадь поверхности отсеченного конуса составляет 9/25 площади поверхности исходного.

12,6

Площадь полной поверхности конуса равна 32,5. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 4:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса .

20,8

Площадь полной поверхности конуса равна 15. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 2:3, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.  

2,4

Диаметр основания конуса равен 40, а длина образующей – 25. Найдите высоту конуса.

R = D/2. R = 20. В прямоугольном треугольнике АОВ АО 2 + ОВ 2 = АВ 2 . АО 2 + 20 2 = 25 2 . АО = . А0 = 15

15

Высота конуса равна 21, а длина образующей равна 29. Найдите диаметр основания конуса.

В прямоугольном треугольнике АОВ АО 2 + ОВ 2 = АВ 2 . 21 2 + ОВ 2 = 29 2 . ОВ = . ОВ = 20. D = 2ОВ. D = 40

40

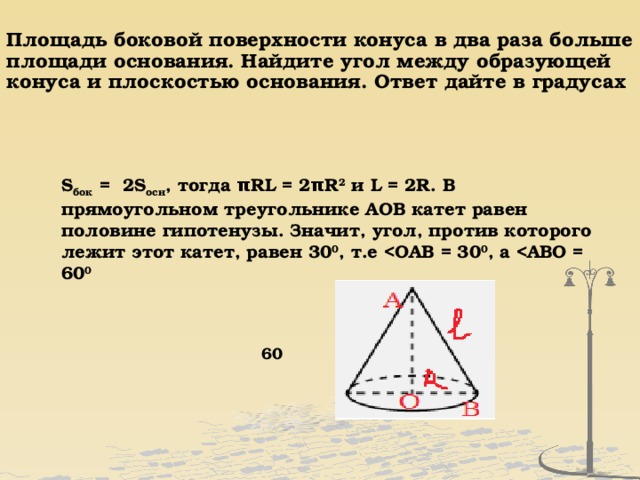
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах

S бок = 2S осн , тогда πRL = 2πR 2 и L = 2R. В прямоугольном треугольнике АОВ катет равен половине гипотенузы. Значит, угол, против которого лежит этот катет, равен 30 0 , т.е 0 , а 0

60

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?

S 1 = πRL , S 2 = πR•3L,

3

Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 2,5 раза, а образующая останется прежней?

• S 1 = πRL , S 2 = •L

2,5