

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 28.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Подготовка к ЕГЭ (профильный уровень)
Категория:
Математика
23.01.2017 17:46
Просмотр содержимого документа
«1912001»
Просмотр содержимого документа
«1912002»
Просмотр содержимого документа
«1912003»
Просмотр содержимого документа
«1912004»
Просмотр содержимого документа
«1912005»
Просмотр содержимого документа
«1912006»
Просмотр содержимого документа
«1912007»
Просмотр содержимого документа
«1912008»
Просмотр содержимого документа
«1912009»
Просмотр содержимого документа
«1912010»
© 2017, Козловская Наталья Александровна 3820 11





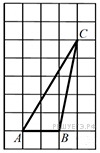
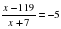
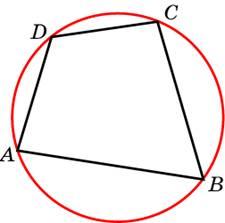
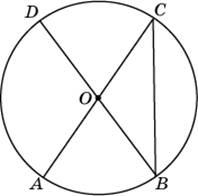
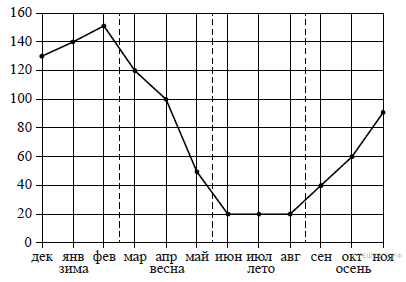
 . Найдите AB.
. Найдите AB.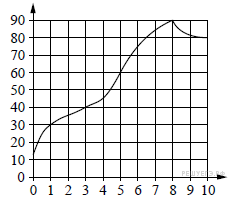
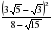 .
.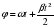 , где t — время в минутах,
, где t — время в минутах, 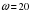 /мин — начальная угловая скорость вращения катушки, а
/мин — начальная угловая скорость вращения катушки, а 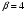 /мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки достигнет 1200. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
/мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки достигнет 1200. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.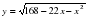 .
.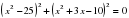
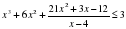
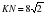 и
и 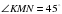

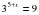
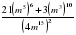 .
.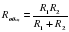 (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в омах.
(Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в омах.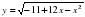
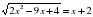
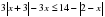
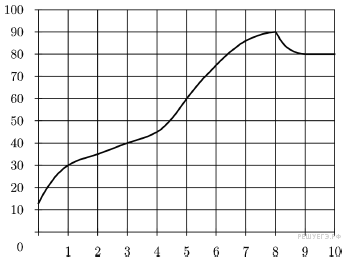
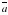 и
и 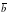 . Ответ дайте в градусах.
. Ответ дайте в градусах.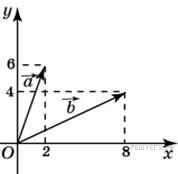
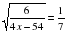 .
.
 , если
, если 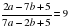 .
.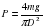 где m = 7500 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая, что ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.
где m = 7500 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая, что ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.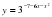
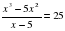
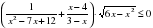
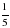 длины катета АС
длины катета АС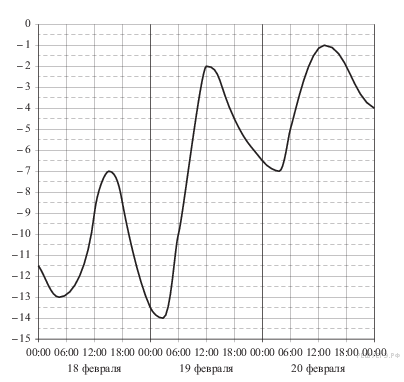
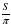 .
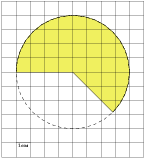
.
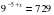 .
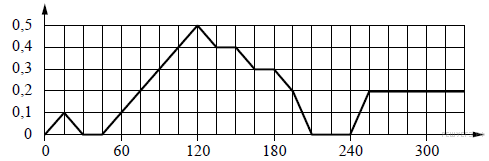
.
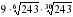 .
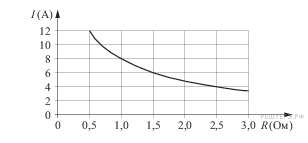
.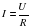 , где U – напряжение в вольтах, R – сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
, где U – напряжение в вольтах, R – сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах. .
.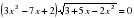
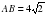 , AD = 12, AA1 = 14.
, AD = 12, AA1 = 14.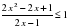
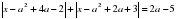
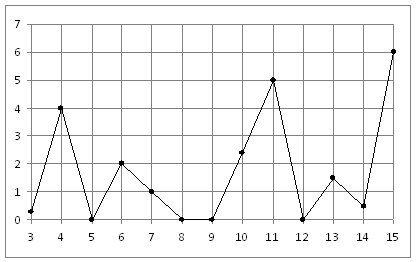
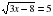 .
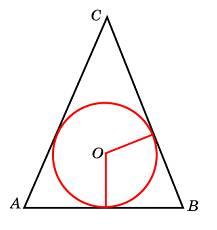
.
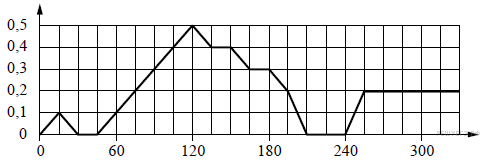
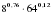 .
.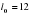 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону
м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону  , где
, где  (С)-1 - коэффициент теплового расширения, t — температура (в градусах Цельсия). При какой температуре рельс удлинится на 9 мм? Ответ выразите в градусах Цельсия.
(С)-1 - коэффициент теплового расширения, t — температура (в градусах Цельсия). При какой температуре рельс удлинится на 9 мм? Ответ выразите в градусах Цельсия.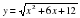
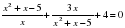

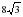 и ∠BAC = 60°.
и ∠BAC = 60°.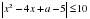 выполняется для всех
выполняется для всех 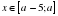
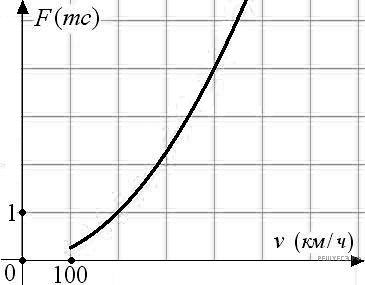
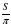 .
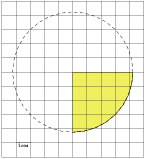
.
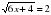 .
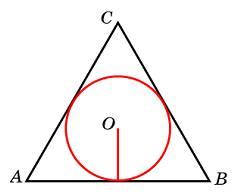
.
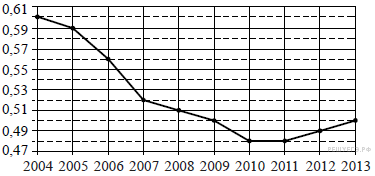
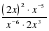 .
.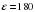 В и внутренним сопротивлением
В и внутренним сопротивлением 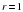 Ом, хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, задается формулой
Ом, хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, задается формулой 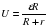 . При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 170 В? Ответ выразите в омах.
. При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 170 В? Ответ выразите в омах.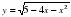 .
.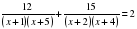
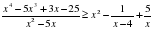
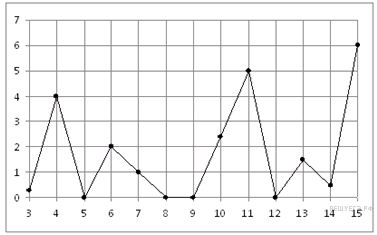

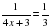 .
.
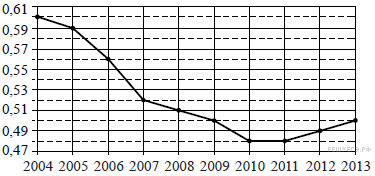
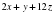 , если
, если 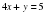 , а
, а 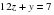 .
.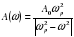 , где — частота вынуждающей силы (в с-1), А0 — постоянный параметр, р = 300 с-1 — резонансная частота. Найдите максимальную частоту , меньшую резонансной, для которой амплитуда колебаний превосходит величину А0 не более чем на 80%. Ответ выразите в с-1.
, где — частота вынуждающей силы (в с-1), А0 — постоянный параметр, р = 300 с-1 — резонансная частота. Найдите максимальную частоту , меньшую резонансной, для которой амплитуда колебаний превосходит величину А0 не более чем на 80%. Ответ выразите в с-1.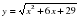 .
.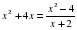
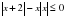
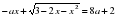 имеет единственный корень
имеет единственный корень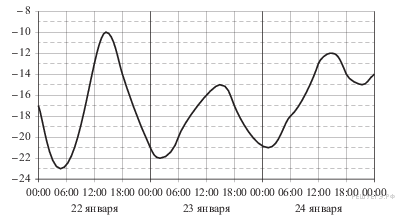
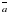 и
и 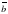 .
.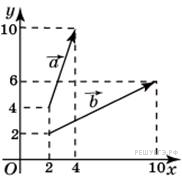
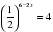 .
.
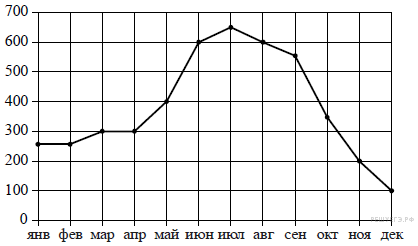
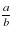 , если
, если 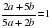
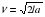 , где l — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость 110 км/ч. Ответ выразите в км/ч2 .
, где l — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость 110 км/ч. Ответ выразите в км/ч2 .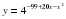 .
.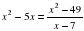
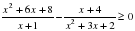
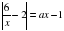 на промежутке
на промежутке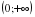 имеет более двух корней.
имеет более двух корней.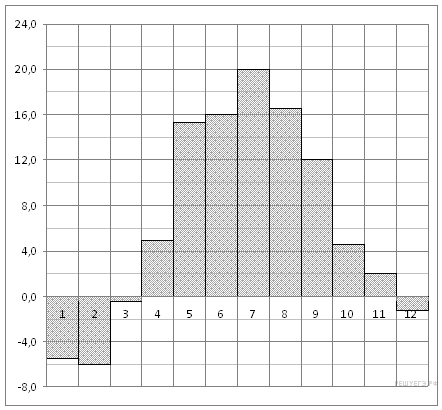
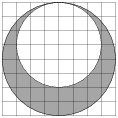
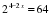 .
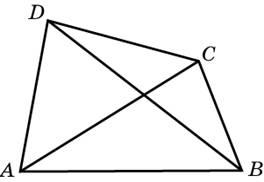
.
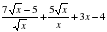 при х = 3.
при х = 3.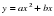 , где
, где 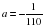 м-1,
м-1, 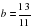 — постоянные параметры, х (м) — смещение камня по горизонтали, у (м) — высота камня над землей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 19 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
— постоянные параметры, х (м) — смещение камня по горизонтали, у (м) — высота камня над землей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 19 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?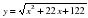 .
.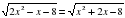
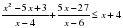
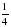 длины катета АС
длины катета АС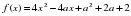 на множестве
на множестве 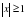 не меньше 6
не меньше 6
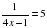 .
.
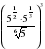 .
.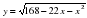 .
.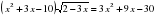
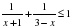
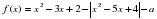 пересекает ось абсцисс менее чем в трех различных точках.
пересекает ось абсцисс менее чем в трех различных точках.




















