Доклад на тему :
«Подготовка к ОГЭ по математике»
Выполнила: учитель математики
(МКОУ «Чермошнянская ООШ»
Солнцевского района Курской области
Фролова Г.И.
Чермошное-2017
В задания по математике ОГЭ включаются задачи, которые либо изучались давно, либо на их изучение отводилось малое количество времени (проценты, стандартный вид числа, свойства числовых неравенств, задачи по статистике, чтение графиков функций), а также задачи, требующие знаний по другим предметам, поэтому важно организовать повторение материала на каждом уроке математики .
Я знакомлю учащихся со структурой теста, временными рамками, нормами оценивания экзаменационной работы, условиями проведения экзамена и начинаю обучать правилам ,которые необходимо соблюдать:
- строгий самоконтроль времени;
- определение трудности заданий;
- проверка результата на правдоподобность.
Обязательно необходимо учитывать индивидуальные особенности детей,использовать дифференцированные задания
Учитывая уровень знаний, в классе определяю три группы.
В первую группу отношу учащихся, знающих программный материал. Они на уроках активны, хорошо владеют приёмами учебного труда, решают почти любые задачи и примеры.
Ко второй группе относятся ребята, имеющие положительные отношения к учению, но слабо владеют приёмами учебного труда. У них есть желание хорошо учиться, однако – многое не получается из-за минимального уровня знаний и умений.
К третьей группе относятся ребята, имеющие слабые знания по материалу, и не владеющие приёмами учебного труда.
На уроках уделяю внимание работе с учебником. Сначала это трудно. Дети не могут выделить главное, уловить смысл прочитанного. Но если работу с учебником проводить систематически, то появляется результат – ребята особенно сильные, внимательно читают и быстро находят ответы на вопросы.
Проводятся тренировочные работы, позволяющие проверить уровень усвоения материала, заведены папки, в которых находятся КИМы, их решения, мониторинг, который позволяет проводить отслеживание результативности каждого учащегося.
Индивидуальные консультации по запросу учащихся провожу ежедневно. Неотъемлемым элементом подготовки к ОГЭ является обучение заполнению бланков ,психологические упражнение ,ведь часто учащиеся не могут сконцентрировать внимание и выполнить упражнение, хотя прекрасно знают весь теоретический материал по данной теме.
Родителей учащихся знакомлю с процедурой подготовки и проведения экзаменов, с результатами их детей в решении тестов.
Наиболее чаще я использую в работе сайт https://sdamgia.ru/ «РЕШУ ОГЭ»: математика. Обучающая система Дмитрия Гущина ,который содержит задания по всем темам, которые необходимо повторить к окончанию уровня основного общего образования . Например , следующие разделы содержат подразделы
| 1.Числа и вычисления 2.Числовые неравенства, координатная прямая | 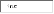  Неравенства Неравенства
| | |   Сравнение чисел Сравнение чисел
| | |   Числа на прямой Числа на прямой
| | |   Выбор верного или неверного утверждения Выбор верного или неверного утверждения
|
|
|
Во второй части у ребят вызывают затруднения следующие задания:
Задания 21 (C1). Алгебраические выражения, уравнения, неравенства и их системы
Алгебраические выражения
1.Сократите дробь , если . 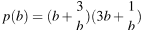
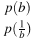
Решение.
Имеем:
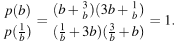
Ответ: 1.
2. Найдите значение выражения ![]()
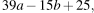 если
если 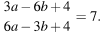
Преобразуем равенство 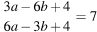 так, чтобы оно содержало выражение
так, чтобы оно содержало выражение 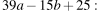
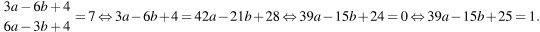
Ответ: 1.
Тема: Неравенства
Решите неравенство
Задание 21 № 311237
Решение.
Определим знак разности  . Так как
. Так как  и
и  , то
, то  .
.
( Без таких пояснений учащиеся теряли баллы)
2) Получаем неравенство  . Отсюда
. Отсюда  .
.
Ответ:  . Другая возможная форма ответа:
. Другая возможная форма ответа:
Тема :уравнения.
Решите уравнение .
Задание 21 № 311618
Решение.
Квадрат любого числа неотрицателен. Сумма двух неотрицательных чисел равна нулю, только если они оба равны нулю. Получаем систему уравнений:
Из первого уравнения 
![]() или
или 
![]() .
.
Из второго уравнения  или
или  .
.
Системе удовлетворяет единственное значение  .
.
Ответ: −5.
Решите уравнение
Задание 21 № 338079
Решение.
Преобразуем уравнение:
Ответ: 4; 5.
Задачи на смеси и сплавы удобно решать ,используя метод Пирсона
При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?




 45 5
45 5
55%
![]() 60 10
60 10
10/5=2/1
Также этот портал удобен и для самостоятельной работы ,он содержит функцию проверки результата, показа подробного решения, возможности прорешивать весь тест, или выбрать определенные темы, вызывающие затруднения
Только совместная кропотливая работа учителя и учащихся при поддержке родителей при изучении всего курса математики ,начиная с первого класса ,может привести к успеху.








 Действия с обыкновенными дробями
Действия с обыкновенными дробями  Действия с десятичными дробями
Действия с десятичными дробями 



















