Подготовка к ОГЭ по математике

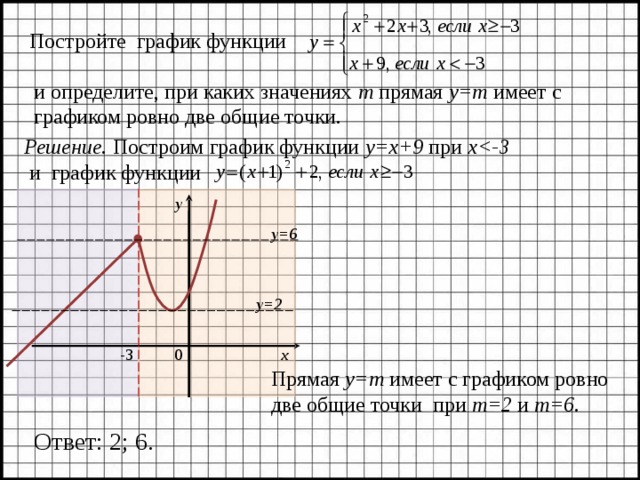
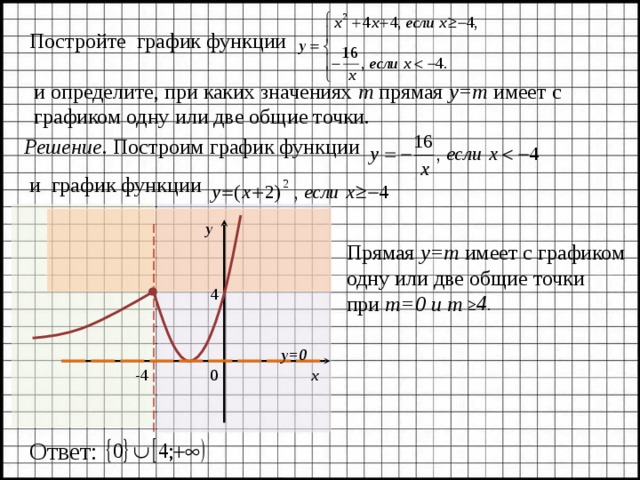
Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.

Решение. Построим график функции

и график функции

y

Прямая y=m имеет с графиком

одну или две общие точки

при m =0 и m

4

≥ 4 .

y= 0

-4

0

x

Ответ:

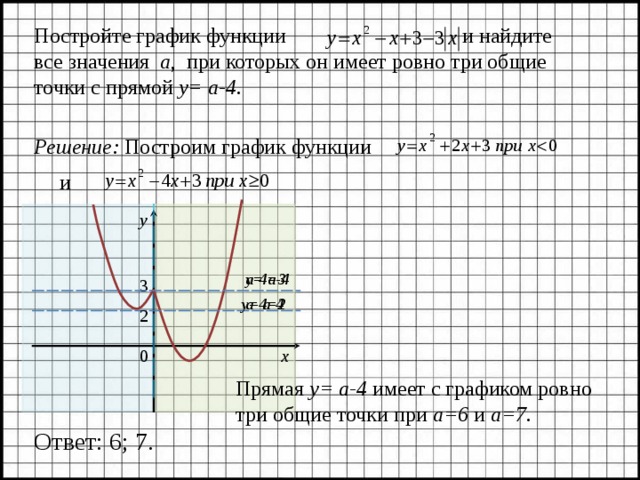
Постройте график функции и найдите все значения а , при которых он имеет ровно три общие точки с прямой y= а-4 .

Решение: Построим график функции

и

у

а-4=3

y= а-4

3

а-4=2

y= а-4

2

х

0

Прямая y= а-4 имеет с графиком ровно три общие точки при а=6 и а=7 .

Ответ: 6; 7.

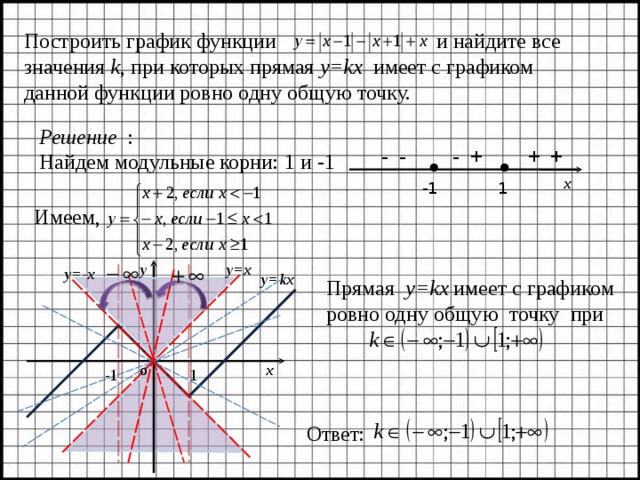
Построить график функции и найдите все значения k , при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.

Решение :

Найдем модульные корни: 1 и -1

- -

- +

+ +

х

-1

1

Имеем,

у=х

у

у=-х

у= k х

Прямая у= k х имеет с графиком

ровно одну общую точку при

о

х

1

-1

Ответ:

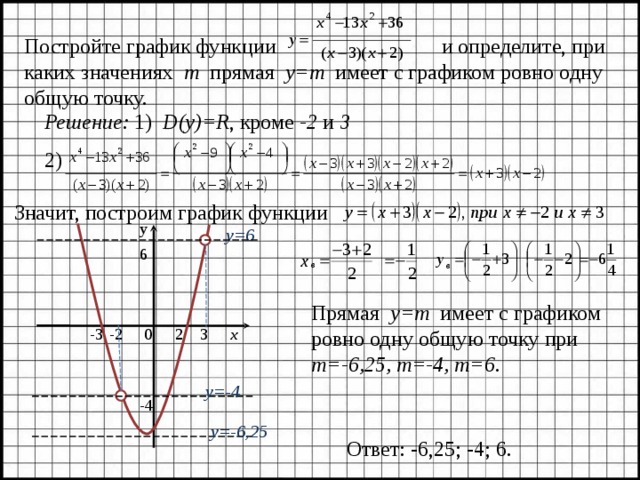
Постройте график функции и определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.

Решение: 1) D(y)=R , кроме -2 и 3

2)

Значит, построим график функции

у

у=6

6

Прямая y = m имеет с графиком ровно одну общую точку при m =-6,25, m =-4, m =6.

х

2

-3

-2

3

0

у=-4

-4

у=-6,25

Ответ: -6,25; -4; 6.

Постройте график функции    . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Решение:

График данной функции — это график параболы   ,

отрицательная часть которого отражена относительно оси   Ох

Прямая, параллельная оси абсцисс задаётся формулой  у=с  , где  с  — постоянная.

у

у=с

Из графика видно, что прямая  у=с  может иметь с графиком функции не более четырёх общих точек.

х

0

-1

2

Ответ: 4

Спасибо за внимание.