| 1 | | На окружности отмечены точки A и B так, что меньшая дуга AB равна 168°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах. |
| 2 | | Сторона равностороннего треугольника равна 4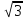 . Найдите радиус окружности, описанной около этого треугольника. . Найдите радиус окружности, описанной около этого треугольника. |
| 3 | | Сторона равностороннего треугольника равна 14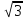 . Найдите радиус окружности, вписанной в этот треугольник. . Найдите радиус окружности, вписанной в этот треугольник. |
| 4 | | Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника. |
| 5 | | Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника. |
| 6 | | Радиус окружности, вписанной в равносторонний треугольник, равен 5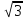 . Найдите длину стороны этого треугольника. . Найдите длину стороны этого треугольника. |
| 7 | | Радиус окружности, описанной около равностороннего треугольника, равен. 8 Найдите длину стороны этого треугольника. Найдите длину стороны этого треугольника. |
| 8 | | Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, AC=8. Найдите AK |
| 9 | | Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, BC=12. Найдите AK |
| 10 | | Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP. |
| 11 | | Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD. |
| 12 | | Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=10, DK=6, BC=15. Найдите AD. |
| 13 | | В треугольнике ABC угол C равен 60°, AB=12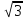 . Найдите радиус окружности, описанной около этого треугольника. . Найдите радиус окружности, описанной около этого треугольника. |
| 14 |
| Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=12, а расстояния от центра окружности до хорд AB и CD равны соответственно 8 и 6. |
|
|
| Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24. |
|
|
| Углы B и C треугольника ABC равны соответственно 62° и 88°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 12. |
|
| | Четырёхугольник ABCD вписан в окружность. Угол ABD равен 80°, угол CAD равен 34°. Найдите угол ABC. Ответ дайте в градусах. |
|
| | В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах. |
|
| | На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах. |
|
| | Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=56° и ∠OAB=15°. Найдите угол BCO. Ответ дайте в градусах. |
|
| | Касательные в точках A и B к окружности
с центром в точке O пересекаются под углом 52°. Найдите угол ABO. Ответ дайте в градусах. |
|
| | Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите угол BOC. Ответ дайте в градусах. |
|
| | Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=107°. Найдите угол BOC. Ответ дайте в градусах. |
|
| | Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах. |
|
| | Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 67°. Ответ дайте в градусах. |
|
| | В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 148°. Найдите угол ACB. Ответ дайте в градусах. |
|
| | Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD. Ответ дайте в градусах. |
|
| | На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=122°. Длина меньшей дуги AB равна 61. Найдите длину большей дуги AB. |
|
| | Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 9°. Ответ дайте в градусах. |
|
| | Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32. |







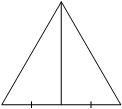
 . Найдите медиану этого треугольника.
. Найдите медиану этого треугольника.
 Найдите AC.
Найдите AC.