Подготовка к ЕГЭ: "Методы решения стереометрических задач"

Методы решения стереометрических задач

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ФАКТЫ

Аксиомы стереометрии

А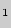. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

А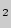. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

А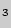. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия:

1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Параллельность в пространстве

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема: Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Теорема: Если две прямые параллельны третьей прямой, то они параллельны.

Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек.

Признак параллельности прямой и плоскости: если прямая, не лежащая в данной плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Признак скрещивающихся прямых: Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Определение: Плоскости называются параллельными, если они не пересекаются.

Признак параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Перпендикулярность в пространстве

Определение: Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен .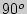

Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Если две прямые перпендикулярны к плоскости, то они параллельны.

Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

Определение: Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

Определение: Двугранный угол - это фигура, образованная прямой 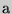и двумя полуплоскостями с общей границей 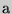, не принадлежащими одной плоскости.

Определение: Перпендикулярные плоскости - это пересекающиеся плоскости, угол между которыми равен .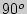

Признак перпендикулярности двух плоскостей: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Теорема Эйлера для многогранников: в любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2.

Существует 5 видов правильных многогранников: тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр.

ОСНОВНЫЕ ФОРМУЛЫ

1. Произвольная призма (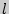 - боковое ребро; 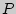- периметр основания; 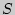- площадь основания; 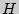- высота призмы; 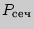- периметр перпендикулярного сечения; 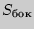- площадь боковой поверхности; 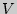- объем): ; .

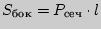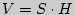2. Прямая призма: ; .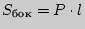

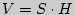3. Прямоугольный параллелепипед (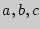 - его измерения; 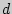- диагональ):

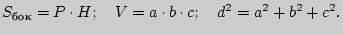
4. Куб (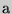 - ребро): ; ; ; .

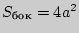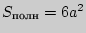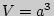5. Произвольная пирамида (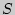 - площадь основания; 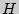- высота пирамиды;
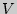- объем): .

6. Правильная пирамида (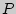 - периметр основания; 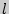- апофема; 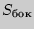- площадь боковой поверхности; 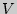- объем): ; .

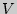7. Произвольная усеченная пирамида ( и - площади оснований; - высота пирамиды; - объем): .

8. Правильная усеченная пирамида ( и - периметры оснований; 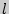- апофема; 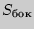- площадь боковой поверхности): .

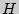9. Цилиндр ( - радиус основания; - высота; 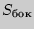- площадь боковой поверхности; 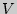- объем): ; .

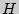10. Конус ( - радиус основания; - высота; 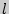- образующая; 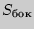- площадь боковой поверхности; 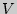- объем): ; .

11. Шар, сфера ( - радиус шара; - площадь сферической поверхности;
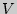- объем): ; .

12. Шаровой сегмент ( - радиус шара; - высота сегмента; - площадь сферической поверхности сегмента; 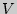- объем): ; .

13. Шаровой сектор ( - радиус шара; - высота сегмента; 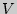- объем): .

ВЕКТОРЫ И КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ

Определение: Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется направленным отрезком или .

Определение: Длиной (модулем) ненулевого вектора называется длина отрезка ; обозначается .

Определение: Ненулевые векторы называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.

Нулевой вектор считается коллинеарным любому вектору.

Коллинеарные векторы могут быть сонаправленными и противоположно направленными.

Определение: Векторы называются равными, если они сонаправлены и их длины равны.

Правила сложения векторов:

Свойства операций над векторами:

1. .

2. .

3. .

4. .

5. .

6. .

Разложение вектора по координатным векторам и :

На плоскости: ; где координаты вектора .

В пространстве: ; где координаты вектора .

На плоскости: если , , то ; .

В пространстве: если и , то

Для отрезка на плоскости координаты его середины связаны с координатами его концов и , так что .

В пространстве: и , так что

Длина (модуль) вектора на плоскости задается формулой: .

В пространстве: если , то .

Расстояние между точками и на плоскости

В пространстве: если и , то

Уравнение окружности: , где - центр окружности, - радиус.

Уравнение прямой .

Скалярное произведение векторов: , где - угол между векторами и . Скалярное произведение в координатах:

На плоскости: ;

В пространстве: .

Свойства скалярного произведения векторов:

1. , если .

2. .

3. .

4. .

2