Подготовка к ЕГЭ по информатике №2

Преобразование логических выражений

ЕГЭ №2

Группа № 10

Греб Тамара Михайловна, ФМШ ГБОУ «Школа №2107»

Тема урока. ЕГЭ №15

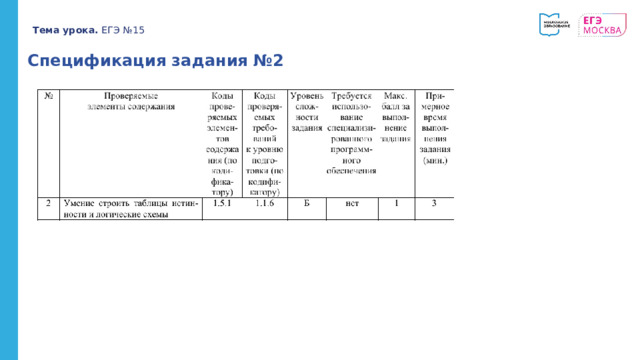
Спецификация задания №2

Тема урока. ЕГЭ №15

Типичные ошибки и рекомендации по их предотвращению:

"Важно понимать, что выражение должно быть тождественно истинно, т.е. истинно при любых допустимых значениях переменных x и у , а не только при некоторых наборах значений"

ФГБНУ "Федеральный институт педагогических измерений"

Тема урока. ЕГЭ №2

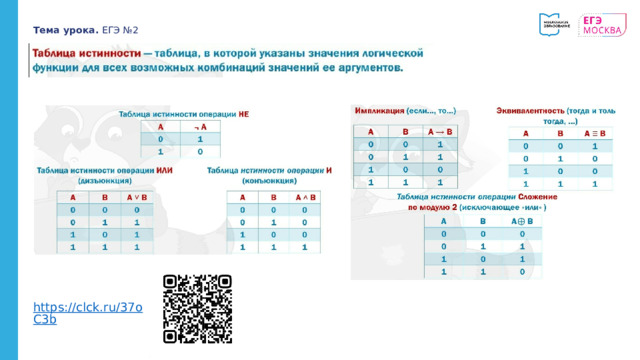
Тема урока. ЕГЭ №2

Правило составления таблицы истинности для логического выражения

Тема урока. ЕГЭ №2

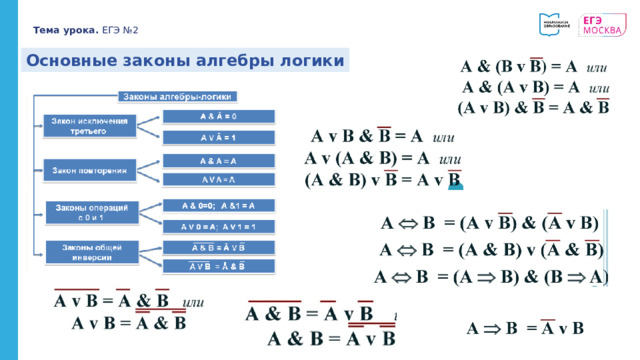
Основные законы алгебры логики

Тема урока. ЕГЭ №2

Пример построения таблицы истинности логической функции

• Вычислить количество строк и столбцов ( n - количество логических переменных Кол-во строк: Str = 2 n + заголовок Кол-во столбцов: Stb = кол-во переменных +кол-во операций

1

2

F(A,B,C)=( A V B)  C

• Str = 2 3 + 1=9
• Stb = 3 +2=5

таблица размером: 5Х9

A

0

B

0

C

0

0

0

0

A V B

1

0

1

F

0

0

1

0

1

1

1

1

1

0

1

1

0

1

0

0

1

1

1

1

1

0

1

1

1

1

1

1

0

1

1

Тема урока. ЕГЭ №2

Тема урока. ЕГЭ №2

Таблица истинности

Таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных. Если известна только часть таблицы истинности , соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных).

Количество разных логических функций , удовлетворяющих неполной таблице истинности, равно 2 k , где k — число отсутствующих строк.

Например, полная таблица истинности выражения с тремя переменными содержит 2 3 = 8 строчек; если заданы только 6 из них, то можно найти 2 8−6 = 2 2 = 4 разные логические функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся).

Тема урока. ЕГЭ №2

Таблица истинности. Задание №1.

Каждое логическое выражение A и B зависит от одного и того же набора из 6 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы . Каково минимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?

Решение: 4&4 = 4

https://youtu.be/-vk0fG-qpuI?t=476

Ответ: 4

Тема урока. ЕГЭ №2

Таблица истинности. Задание №2.

Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы . Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B ?

Решение: 4+4 = 8

https://youtu.be/-vk0fG-qpuI?t=476

Ответ: 8

Тема урока. ЕГЭ №2

Таблица истинности. Задание №3.

Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 5 единиц . Каково минимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B ?

Решение: 2 8 = 256 — 5 = 251

https://youtu.be/-vk0fG-qpuI?t=476

Ответ: 251

Тема урока. ЕГЭ №2

Таблица истинности. Задание №4.

Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц . Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B ?

Решение: 2 8 = 256

https://youtu.be/-vk0fG-qpuI?t=476

Ответ: 256

Тема урока. ЕГЭ №2

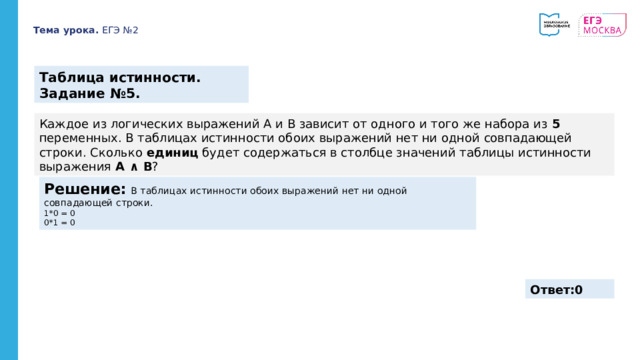
Таблица истинности. Задание №5.

Каждое из логических выражений A и B зависит от одного и того же набора из 5 переменных. В таблицах истинности обоих выражений нет ни одной совпадающей строки. Сколько единиц будет содержаться в столбце значений таблицы истинности выражения A ∧ B ?

Решение: В таблицах истинности обоих выражений нет ни одной совпадающей строки.

1*0 = 0

0*1 = 0

https://youtu.be/-vk0fG-qpuI?t=476

Ответ:0

Тема урока. ЕГЭ №2

Таблица истинности. Задание №6.

Каждое из логических выражений A и B зависит от одного и того же набора из 6 переменных. В таблицах истинности обоих выражений нет ни одной совпадающей строки. Сколько единиц будет содержаться в столбце значений таблицы истинности выражения A ∨ B ?

Решение: 2 6 = 64

https://youtu.be/-vk0fG-qpuI?t=476

Ответ: 64

¬0 ∨ 0 = 0 + 0 = 0 2 7 = 128 https://youtu.be/-vk0fG-qpuI?t=476 Ответ:128 " width="640"

Тема урока. ЕГЭ №2

Таблица истинности. Задание №7.

Каждое из логических выражений A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности обоих выражений нет ни одной совпадающей строки. Каково максимально возможное число нулей в столбце значений таблицы истинности выражения ¬A ∨ B ?

Решение: ¬A ∨ B

A=1,B=0 = ¬0 ∨ 0 = 0 + 0 = 0

2 7 = 128

https://youtu.be/-vk0fG-qpuI?t=476

Ответ:128

Тема урока. ЕГЭ №2

Таблица истинности. Задание №8.

Каждое из логических выражений A и B зависит от одного и того же набора из 6 переменных. В таблицах истинности обоих выражений нет ни одной совпадающей строки. Сколько единиц будет содержаться в столбце значений таблицы истинности выражения A ∨ B ?

Решение: 2 6 = 64

https://youtu.be/-vk0fG-qpuI?t=476

Ответ: 64

Тема урока. ЕГЭ №2

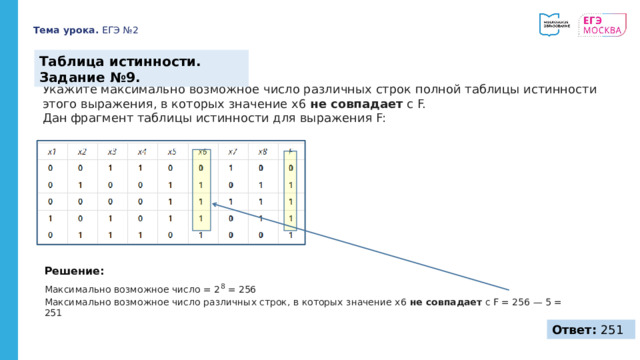
Таблица истинности. Задание №9.

Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x6 не совпадает с F.

Дан фрагмент таблицы истинности для выражения F:

Решение:

Максимально возможное число = 2 8 = 256

Максимально возможное число различных строк, в которых значение x6 не совпадает с F = 256 — 5 = 251

Ответ: 251

Тема урока. ЕГЭ №2

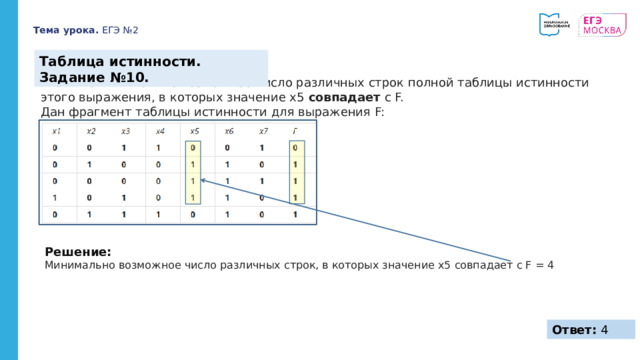
Таблица истинности. Задание №10.

Укажите минимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x5 совпадает с F.

Дан фрагмент таблицы истинности для выражения F:

Решение:

Минимально возможное число различных строк, в которых значение x5 совпадает с F = 4

Ответ: 4

Тема урока. ЕГЭ №2

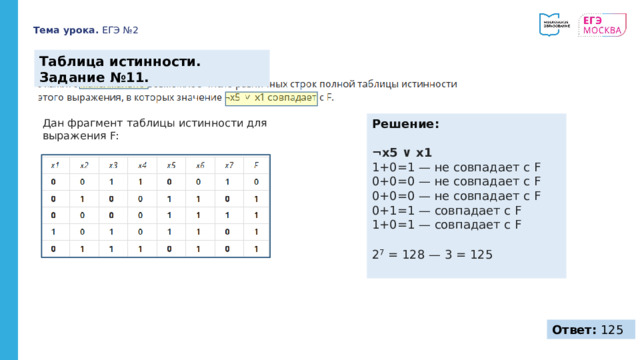
Таблица истинности. Задание №11.

Дан фрагмент таблицы истинности для выражения F:

Решение:

¬x5 ∨ x1

1+0=1 — не совпадает с F

0+0=0 — не совпадает с F

0+0=0 — не совпадает с F

0+1=1 — совпадает с F

1+0=1 — совпадает с F

2 7 = 128 — 3 = 125

Ответ: 125

Тема урока. ЕГЭ №2

Решение:

Таблица истинности. Задание №12.

• Поскольку в каждом из выражений присутствует 8 переменных, то эти 8 переменных порождают таблицу истинности из 256 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с 8 переменными будет 2 8 =256 т.е. 256 строки.
• Из этих 256 строк и для F и для G мы знаем наверняка только о 7 строках: 3 из них истинны (=1), а 4 -ложны (=0).

Каждое из логических выражений F и G содержит 8 переменных. В таблицах истинности

выражений F и G есть ровно 7 одинаковых строк, причем ровно в 3 из них в столбце значений стоит 1. Сколько строк таблицы истинности для выражения F∧G содержит 0 в столбце значений?

• Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G . Данная операция — коньюнкция, которая истина только в одном случае — если F = 1 и одновременно G = 1
• В исходных таблицах для F и G мы знаем о существовании только 3 единиц, т.е. в остальных строках может быть 0. Т.о., и для F и для G в 256 строке могут быть нули ( 256-3=253 ), а лишь в 3— единицы.

Ответ: 253

Тема урока. ЕГЭ №2

Решение:

Таблица истинности. Задание №13.

• Поскольку в каждом из выражений присутствует 7 переменных, то эти 7 переменных порождают таблицу истинности из 128 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с 7 переменными будет 2 7 =128 т.е. 128 строки.
• Из этих 128 строк и для F и для G мы знаем наверняка только о 8 строках: 5 из них истинны (=1), а 3 -ложны (=0).

Каждое из логических выражений F и G содержит 7 переменных. В таблицах истинности выражений F и G есть ровно 8 одинаковых строк, причем ровно в 5 из них в столбце значений стоит 1. Сколько строк таблицы истинности для выражения F V G содержит 1 в столбце значений?

• Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G . Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
• В исходных таблицах для F и G мы знаем о существовании только 3 нулей, т.е. в остальных строках может быть 1 . Т.о., и для F и для G в 125 строке могут быть единицы ( 128-3=125 ), а лишь в 3— ноль.

Ответ: 125

Тема урока. ЕГЭ №2

Решение:

Таблица истинности. Задание №14.

• Поскольку в каждом из выражений присутствует 6 переменных, то эти 6 переменных порождают таблицу истинности из 64 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с 6 переменными будет 2 6 =64 , т.е. 64 строки.
• Из этих 64 строк и для F и для G мы знаем наверняка только о 10 строках: 3 из них истинны (=1), а 7 -ложны (=0).

Каждое из логических выражений F и G содержит 6 переменных. В таблицах истинности выражений F и G есть ровно 10 одинаковых строк, причем ровно в 3 из них в столбце значений стоит 1. Сколько строк таблицы истинности для выражения F V G содержит 1 в столбце значений?

• Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G . Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
• В исходных таблицах для F и G мы знаем о существовании только 7 нулей, т.е. в остальных строках может быть 1 . Т.о., и для F и для G в 57 строке могут быть единицы ( 64-7=57 ), а лишь в семи — ноль.

Ответ: 57

Тема урока. ЕГЭ №2

Закрепление. Самостоятельный ответ. Таблица истинности. Задание №2.

Евгений Джобс, №83 в сборнике Полякова

https://youtu.be/Rq_8-iD1zc0?t=215

Ответ: 61

Тема урока. ЕГЭ №2

Экзамен ЕГЭ по информатике, МЭШ

Решение:

x3 x4

1*1=1 — совпадает с F

0*0=0 — не совпадает с F

1*0=0 — не совпадает с F

1*1=1 — не совпадает с F

2 6 = 64 — 1 = 63

Дан фрагмент таблицы истинности для выражения F:

Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в котором значение выражения x3 x4 не совпадает с F

Ответ: 63

Реальный ЕГЭ

Задание №2

Тема урока. ЕГЭ №2

Способы решения задания ЕГЭ №2:

• с помощью логического рассуждения;
• с помощью упрощения логического выражения
• с помощью электронных таблиц;
• с помощью языка программирования (Python).

Тема урока. ЕГЭ №2

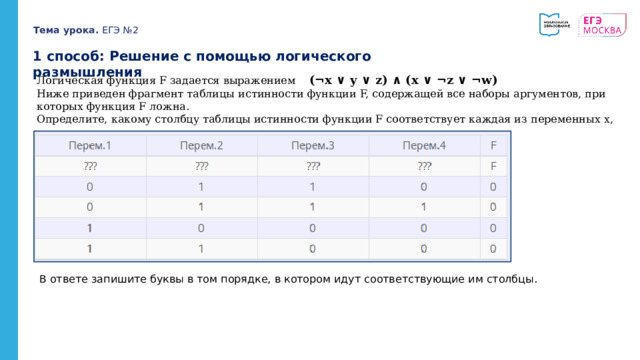
1 способ: Решение с помощью логического размышления

Логическая функция F задается выражением (¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

Тема урока. ЕГЭ №2

1 способ: Решение с помощью логического размышления

• Внешняя операция выражения — конъюнкция ( ∧ ). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна ( = 1 ) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:

Логическая функция F задается выражением (¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

2. Общая идея дальнейшего решения такова: поскольку внешняя операция — конъюнкция, и результат ее истинен, когда оба сомножителя в скобках будут истинны (=1), то нам необходимо сначала составить все наборы таблицы истинности для обоих сомножителей в скобках. Затем, так как конъюнкция подразумевает пересечение, необходимо сопоставить обе таблицы истинности и выбрать для каждого подходящего набора первого сомножителя подходящий (подходящие) набор (наборы) второго сомножителя. НО! т ак как у нас в задании известны только наборы для F = 0 , то мы сопоставлять будем наборы, которые возвращают ложь. Теперь подробно.

Разобьём исходное выражение на две части и составим таблицу истинности отдельно для двух частей.

Тема урока. ЕГЭ №2

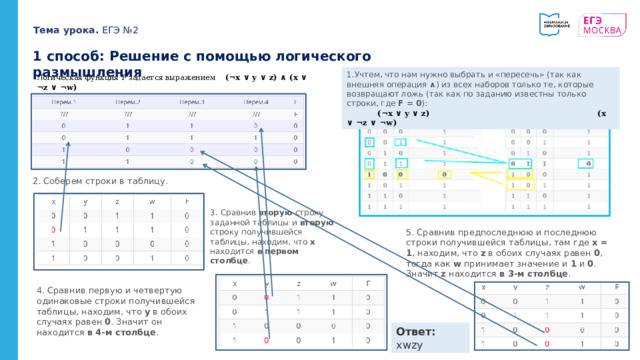
1 способ: Решение с помощью логического размышления

1.Учтем, что нам нужно выбрать и «пересечь» (так как внешняя операция ∧ ) из всех наборов только те, которые возвращают ложь (так как по заданию известны только строки, где F = 0 ):

(¬x ∨ y ∨ z) (x ∨ ¬z ∨ ¬w)

Логическая функция F задается выражением (¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

2. Соберем строки в таблицу.

3. Сравнив вторую строку заданной таблицы и вторую строку получившейся таблицы, находим, что x находится в первом столбце .

5. Сравнив предпоследнюю и последнюю строки получившейся таблицы, там где x = 1 , находим, что z в обоих случаях равен 0 , тогда как w принимает значение и 1 и 0 . Значит z находится в 3-м столбце .

4. Сравнив первую и четвертую одинаковые строки получившейся таблицы, находим, что y в обоих случаях равен 0 . Значит он находится в 4-м столбце .

Ответ: xwzy

Тема урока. ЕГЭ №2

2 способ: Решение с помощью электронных таблиц

• Сначала количество столбцов в электронной таблице равно количеству переменных логического выражения. Каждый столбец обозначается по именам переменных логического выражения.
• Затем добавляется количество строк электронной таблицы, равное , где k — количество переменных логического уравнения.
• После этого создается еще один столбец электронной таблицы, в первой строке которого (не заголовка) записывается формула, соответствующая логическому выражению. Растянув эту формулу при помощи маркера автозаполнения на все строки таблицы, получаем полную таблицу истинности выражения.

Таблица функций электронной таблицы Excel и их соответствия логическим операциям:

Логическая операция

Инверсия

Строка Excel

Дизъюнкция

=ЕСЛИ(A2=1;0;1) =ЕСЛИ(НЕ(A2=1);1;0)

=ЕСЛИ(ИЛИ(A2=1;B2=1);1;0)

Конъюнкция

Импликация

=ЕСЛИ(И(A2=1;B2=1);1;0)

Эквивалентность

=ЕСЛИ(И(A2=1;B2=0);0;1)

=ЕСЛИ(A2=B2;1;0)

Тема урока. ЕГЭ №2

2 способ: Решение с помощью электронных таблиц

Логическая функция F задается выражением (¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

Тема урока. ЕГЭ №2

Решение:

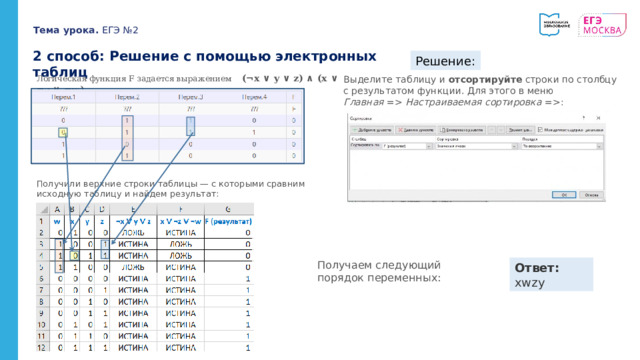
2 способ: Решение с помощью электронных таблиц

Л огическая функция F задается выражением (¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 2 4 =16:

Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

Настраиваемая сортировка =: Получили верхние строки таблицы — с которыми сравним исходную таблицу и найдем результат: Получаем следующий порядок переменных: Ответ: xwzy " width="640"

Тема урока. ЕГЭ №2

2 способ: Решение с помощью электронных таблиц

Решение:

Логическая функция F задается выражением (¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

Выделите таблицу и отсортируйте строки по столбцу с результатом функции. Для этого в меню Главная = Настраиваемая сортировка =:

Получили верхние строки таблицы — с которыми сравним исходную таблицу и найдем результат:

Получаем следующий порядок переменных:

Ответ: xwzy

Тема урока. ЕГЭ №2

эквивалент

эквивалент

⊕ Cтрогая дизъюнкция

!=

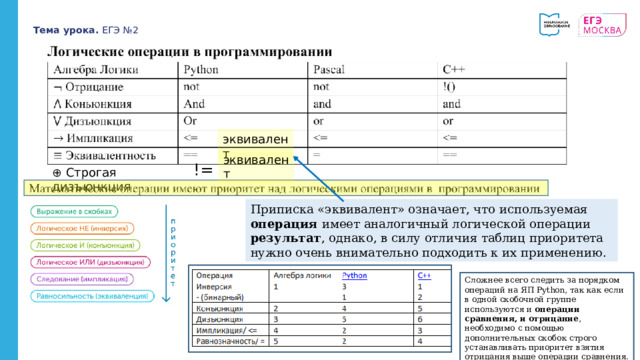
Приписка «эквивалент» означает, что используемая операция имеет аналогичный логической операции результат , однако, в силу отличия таблиц приоритета нужно очень внимательно подходить к их применению.

Сложнее всего следить за порядком операций на ЯП Python, так как если в одной скобочной группе используются и операции сравнения, и отрицание , необходимо с помощью дополнительных скобок строго устанавливать приоритет взятия отрицания выше операции сравнения.

Тема урока. ЕГЭ №2

Рекомендации по оформлению:

• Так как обычно необходимо найти наборы переменных для определенных значений функции , то удобнее сохранить значение в переменную .
• Также можно описать функцию , которая будет возвращать значение выражения. Использую функцию , удобнее сравнивать оригинальное выражение и выражение в задании.
• Использование функции гораздо безопаснее, так как не нужно контролировать приоритет операции сравнения с необходимым значением значения выражения (оборачивать логическое выражение в скобки).

Пример с переменной для ложного значения функции F(x, y, z) = x )

Тема урока. ЕГЭ №2

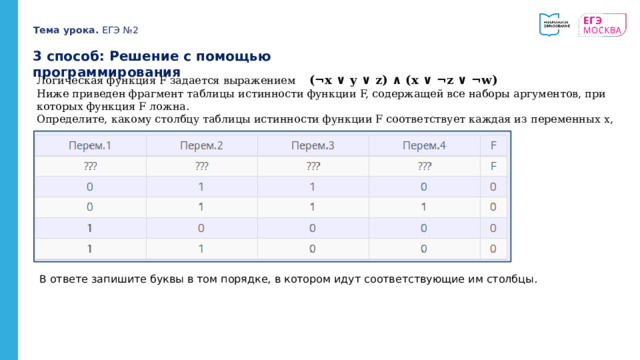
3 способ: Решение с помощью программирования

Логическая функция F задается выражением (¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

Тема урока. ЕГЭ №2

3 способ: Решение с помощью языка программирования Python

Логическая функция F задается выражением (¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

2 способ:

def f(x, y, z, w):

return ((not(x) or y or z) and (x or not(z) or not(w)))

print ('x y w z')

k = 0,1

for x in k:

for y in k:

for w in k:

for z in k:

if f(x, y, w, z)==0:

print(x, y, w, z)

1 способ:

print ('x y z w')

for x in 0, 1:

for y in 0, 1:

for z in 0, 1:

for w in 0, 1:

F = (not(x) or y or z) and (x or not(z) or not(w))

if not (F):

print (x, y, z, w)

3 способ:

from itertools import *

print(‘x y z w’)

for x, y, z, w in product([0, 1], repeat=4):

if (not(x) or y or z) and (x or not(z) or not(w)) == 0:

print(x, y, z, w)

Ответ: xwzy

Тема урока. ЕГЭ №2

Типичная ошибка:

a

d

b

c

a b c d

Решение:

Ответ: сadb

Тема урока. ЕГЭ №2

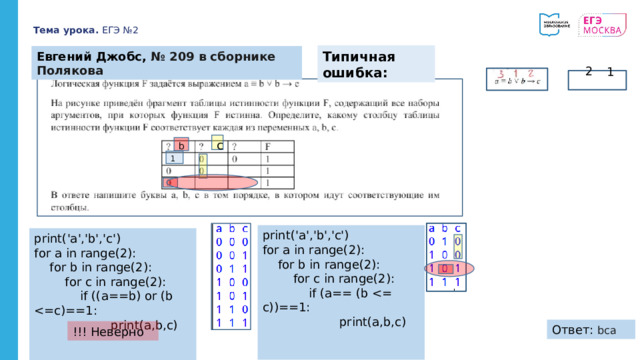
Типичная ошибка:

Евгений Джобс, № 209 в сборнике Полякова

2

1

c

b

1

print('a','b','c')

for a in range(2):

for b in range(2):

for c in range(2):

if (a== (b

print(a,b,c)

print('a','b','c')

for a in range(2):

for b in range(2):

for c in range(2):

if ((a==b) or (b

print(a,b,c)

https://youtu.be/-vk0fG-qpuI?t=476

Ответ: bca

!!! Неверно

Тема урока. ЕГЭ №2

Способ №4. Упрощение логического выражения

Тема урока. ЕГЭ №2

Учимся упрощать сложные логические выражения

Тема урока. ЕГЭ №2

Упрощение логического выражения . Задание №1

Логическая функция F задаётся выражением: (z ∧y))⋁((x→z)≡(y → w)) Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных w,x,y,z

В ответе напишите буквы w,x,y,z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Решение:

Рассмотрим данное выражение. Преобразуем логическое выражение и получим систему, при котором оно ложна

Заметим, что второй столбец таблицы истинности (ТИ) это z, тогда четвертый столбец ТИ - это переменная x. Из условия следует, что переменная y соответствует третьему столбцу ТИ, а переменная w соответствует первому столбцу ТИ.

Ответ: wzyx

Тема урока. ЕГЭ №2

Упрощение логического выражения.

Статград 08.02.2022

Логическая функция F задаётся выражением: (¬y→(z≡w))∧((z→x)≡w) Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных w,x,y,z

В ответе напишите буквы w,x,y,z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Раскроем импликации (y ⋁ (z≡w))∧(( ¬z ⋁ x)≡w)

Раскроем равнозначности (y ⋁ (z ⋀ w ⋁ ¬z ⋀ ¬w))∧((¬z ⋁ x) ⋀ w ⋁ ¬(¬z ⋁ x) ⋀ ¬w)

Раскроем скобки в правом подвыражении (y ⋁ z ⋀ w ⋁ ¬z ⋀ ¬w) ∧ (¬z ⋀ w ⋁ x ⋀ w ⋁ z ⋀ ¬x ⋀ ¬w)

Раскроем оставшиеся скобки y ∧ ¬z ⋀ w ⋁ y ∧ x ⋀ w ⋁ y ⋀ z ⋀ ¬x ⋀ ¬w ⋁ z ⋀ w ⋀ ¬z ⋀ w ⋁ z ⋀ w ⋀ x ⋀ w ⋁ z ⋀ w ⋀ z ⋀ ¬x ⋀ ¬w ⋁ ⋁ ¬z ⋀ ¬w ⋀ ¬z ⋀ w ⋁ ¬z ⋀ ¬w ⋀ x ⋀ w ⋁ ¬z ⋀ ¬w ⋀ z ⋀ ¬x ⋀ ¬w

Сократим все произведения по закону противоречия и правилу идемподентности

y ∧ ¬z ⋀ w ⋁ y ∧ x ⋀ w ⋁ y ⋀ z ⋀ ¬x ⋀ ¬w ⋁ z ⋀ w ⋀ ¬z ⋀ w ⋁ z ⋀ w ⋀ x ⋀ w ⋁ z ⋀ w ⋀ z ⋀ ¬x ⋀ ¬w ⋁ ⋁ ¬z ⋀ ¬w ⋀ ¬z ⋀ w ⋁ ¬z ⋀ ¬w ⋀ x ⋀ w ⋁ ¬z ⋀ ¬w ⋀ z ⋀ ¬x ⋀ ¬w

Получим y ∧ ¬z ⋀ w ⋁ y ∧ x ⋀ w ⋁ y ⋀ z ⋀ ¬x ⋀ ¬w ⋁ z ⋀ w ⋀ x

Тема урока. ЕГЭ №2

Способ №4. Упрощение логического выражения

Статград 08.02.2022

Логическая функция F задаётся выражением: (¬y→(z≡w))∧((z→x)≡w)

F=y ∧ ¬z ⋀ w ⋁ y ∧ x ⋀ w ⋁ y ⋀ z ⋀ ¬x ⋀ ¬w ⋁ z ⋀ w ⋀ x

2) Итого имеем 5 различных наборов.

1) Теперь мы без труда можем найти все наборы, приравняв единице каждое из полученных произведений

3) Сопоставим полученные наборы и фрагмент из задания

4) 1 и 2 строки фрагмента из задания это 2 и 4 строки из полученного фрагмента (без точного соответствия). 3 строка в полученном фрагменте отсутствует в фрагменте из задания. В одном из столбцов должно быть два нуля. Следовательно, третьей строке из фрагмента соответствует 1 строка из полученного фрагмента.

Ответ: zwyx

Решение задач

ЕГЭ №2

Тема урока. ЕГЭ №2

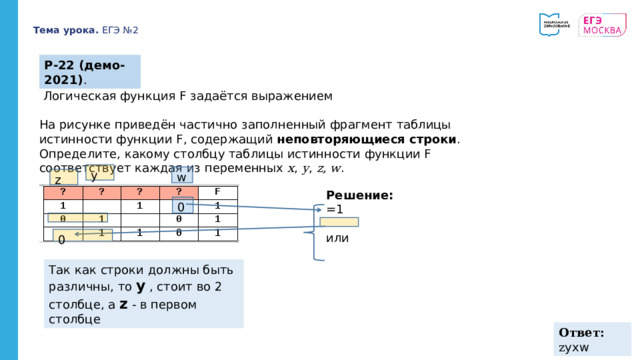
Р-22 (демо-2021) .

Логическая функция F задаётся выражением

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки . Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x , y , z, w .

y

w

z

Решение:

=1

или

0

0

Так как строки должны быть различны, то y , стоит во 2 столбце, а z - в первом столбце

Ответ: z yxw

Тема урока. ЕГЭ №2

Аналитический метод:

Демоверсия ЕГЭ 2024

Данный метод сводится к следующей последовательности действий:

1) Найти наборы переменных, соответствующие данным в таблице,

2) Сопоставить найденные наборы и строки из фрагмента,

3) Определить порядок столбцов во фрагменте

w

y

z

Ответ: wzyx

Тема урока. ЕГЭ №2

Программирование:

Демоверсия ЕГЭ 2024

1 способ:

print(‘x y z w’)

for x in range(2):

for y in range(2):

for z in range(2):

for w in range(2):

if ((x and not y) or (y==z) or not w)==0:

print(x,y,z,w)

z

w

y

1

1

1

1

2 способ:

from itertools import *

for x, y, z, w in product([0, 1], repeat=4):

if ((x and not y) or (y==z) or not w)==0:

print(x, y, z, w)

Ответ: wzyx

Тема урока. ЕГЭ №2

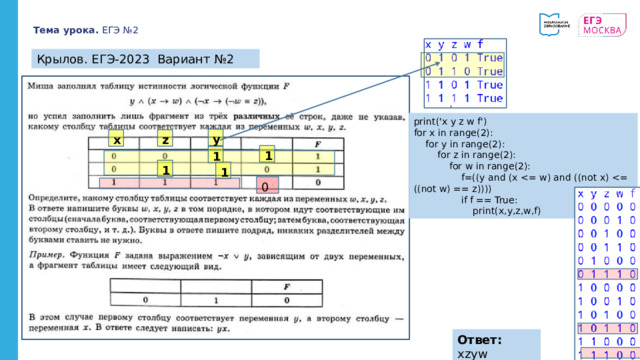
Крылов. ЕГЭ-2023 Вариант №2

print('x y z w f')

for x in range(2):

for y in range(2):

for z in range(2):

for w in range(2):

f=((y and (x

if f == True:

print(x,y,z,w,f)

y

x

z

1

1

1

1

0

Ответ: xzyw

Тема урока. ЕГЭ №2

Задание

Логическая функция F задаётся выражением (a ∧ ¬c) ∨ (¬b ∧ ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.

В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.

Решение: (a * ¬c) + (¬b *¬c)

Когда с равно 1, F равна нулю так что последний столбец c.

Чтобы определить первый и второй столбцы, мы можем использовать значения из 3-го ряда.

0, 1, C=0, F=0

(a * 1) + (¬b * 1) = 0

a=0, b=1.

Ответ: abc

Тема урока. ЕГЭ №2

Задание

Логическая функция F задаётся выражением x ∧ (¬y ∧ z ∧ ¬w ∨ y ∧ ¬z). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Решение: x ∧ (¬y ∧ z ∧ ¬w ∨ y ∧ ¬z)

x * (¬y * z* ¬w + y * ¬z)

Исходя из того, что при x=0, то F=0, мы можем сделать вывод, что во втором столбце располагается x .

(¬y * z* ¬w )==1 или ( y * ¬z ) ==1

из (¬y * z* ¬w )==1 делаем вывод, что z -это 3-ий столбик

х

z

В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.

Ответ: wxzy

Тема урока. ЕГЭ №2

def f1 (x,y,z,w):

if ((x

return 1

else: return 0

def f2 (x,y,z,w):

if ((x

return 1

else: return 0

print('x y z w f1 f2')

for x in range(2):

for y in range(2):

for z in range(2):

for w in range(2):

print(x,y,z,w,"*",f1(x,y,z,w), f2(x,y,z,w))

Статград от 28.03.2023

w

z

x

1

https://www.youtube.com/watch?v=bMvqkiRys5g

https://yandex.ru/video/preview/7145505608285394597

Ответ: xzyw

Тема урока. ЕГЭ №2

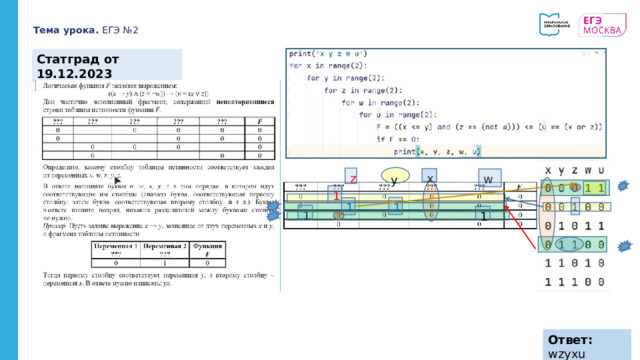
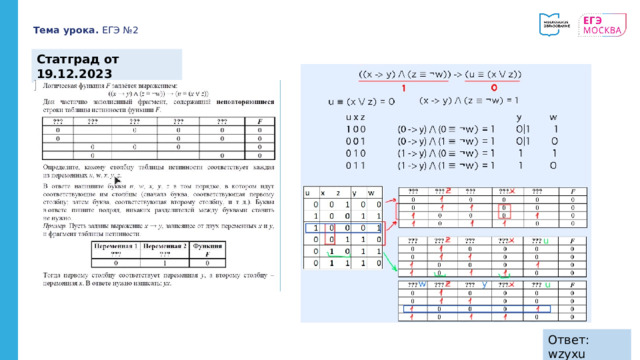
Статград от 19.12.2023

y

z

x

w

1

1

1

1

1

https://www.youtube.com/watch?v=9FgknuSEGNY

Ответ: wzyxu

Тема урока. ЕГЭ №2

Статград от 19.12.2023

https://vk.com/inform_web

Ответ: wzyxu

Тема урока. ЕГЭ №2

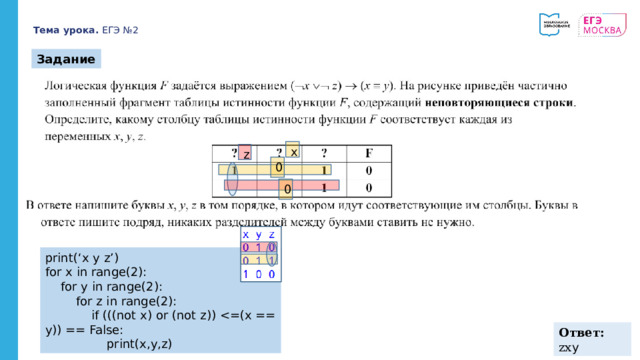
Задание

x

z

0

0

print(‘x y z’)

for x in range(2):

for y in range(2):

for z in range(2):

if (((not x) or (not z))

print(x,y,z)

Ответ: zx y

Тема урока. ЕГЭ №2

Задание

y

z

x

print('x y z w')

for x in range(2):

for y in range(2):

for z in range(2):

for w in range(2):

if (((x and w) or (w and z)) == ((z

print(x,y,z,w)

Ответ : yzwx

Тема урока. ЕГЭ №2

Ответ: cdba.

Практическая работа

35 мин

https://clck.ru/37iWXk

Тема урока. ЕГЭ №2

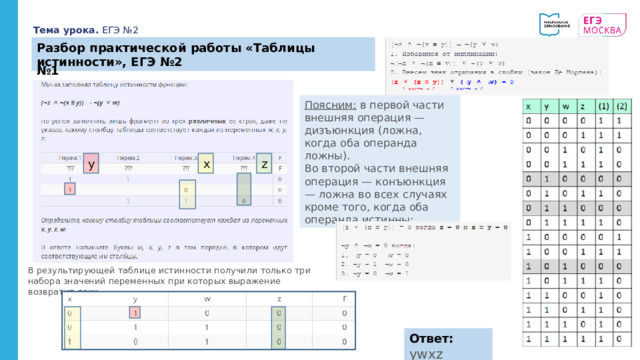
Разбор практической работы «Таблицы истинности», ЕГЭ №2

№ 1

Поясним: в первой части внешняя операция — дизъюнкция (ложна, когда оба операнда ложны). Во второй части внешняя операция — конъюнкция — ложна во всех случаях кроме того, когда оба операнда истинны:

x

z

у

В результирующей таблице истинности получили только три набора значений переменных при которых выражение возвратит ложь.

Ответ: ywxz

Тема урока. ЕГЭ №2

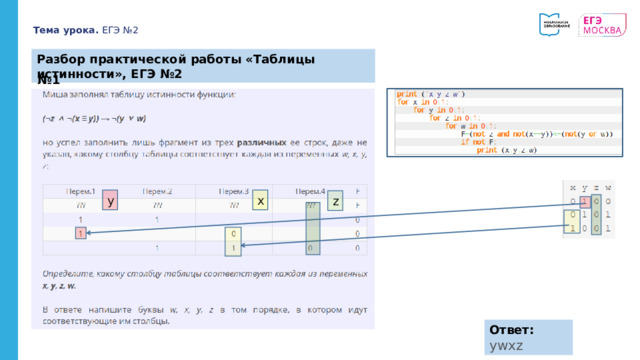
Разбор практической работы «Таблицы истинности», ЕГЭ №2

№ 1

у

x

z

Ответ: ywxz

у

Тема урока. ЕГЭ №2

Разбор практической работы «Таблицы истинности», ЕГЭ №2

№ 2

from itertools import *

print(‘a b c d’)

for a, b, c, d in product([0, 1], repeat=4):

if (not a and b and (c or not d):

print(a, b, c, d)

!!! Удобнее здесь применить метод рассуждения!

b

a

Ответ: cbad

Тема урока. ЕГЭ №2

Разбор практической работы «Таблицы истинности», ЕГЭ №2

№ 3

from itertools import *

print(‘x y z w’)

for x, y, z, w in product([0, 1], repeat=4):

if not(not x or y or(not z and w)):

print(x, y, z, w)

у

x

z

Ответ: xzwy

Тема урока. ЕГЭ №2

Разбор практической работы «Таблицы истинности», ЕГЭ №2

№ 4

from itertools import *

print(‘x y z w’)

for x, y, z, w in product([0, 1], repeat=4):

if not((x and not y ) or (y ==z) or not w):

print(x, y, z, w)

w

x

z

Ответ: xwzy

Тема урока. ЕГЭ №2

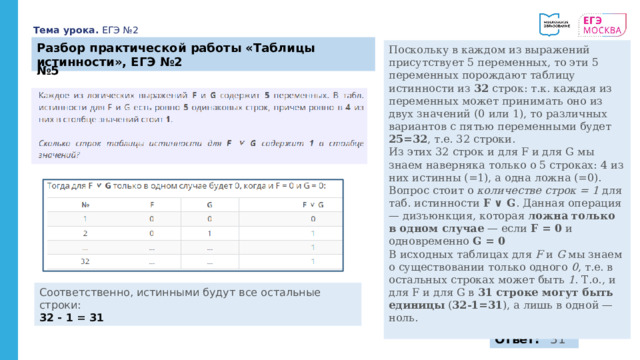
Разбор практической работы «Таблицы истинности», ЕГЭ №2

Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32 , т.е. 32 строки.

Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).

Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G . Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0

В исходных таблицах для F и G мы знаем о существовании только одного 0 , т.е. в остальных строках может быть 1 . Т.о., и для F и для G в 31 строке могут быть единицы ( 32-1=31 ), а лишь в одной — ноль.

№ 5

Соответственно, истинными будут все остальные строки:

32 - 1 = 31

Ответ: 31

Тема урока. ЕГЭ №2

Разбор практической работы «Таблицы истинности», ЕГЭ №2

№ 6

Каждое из логических выражений F и G содержит 7 переменных. В таблицах истинности выражений F и G есть ровно 8 одинаковых строк, причем ровно в 5 из них в столбце значений стоит 1. Сколько строк таблицы истинности для выражения F ∨ G содержит 1 в столбце значений?

Решение:

Есть ровно 8 одинаковых строк, причем ровно в 5 из них в столбце значений стоит 1.

Это означает, что ровно в 3 из них в столбце значений стоит 0.

2 7 = 128

128 — 3 = 125

Ответ: 125

Тема урока. ЕГЭ №2

Методические рекомендации Е. Джобса

https://clck.ru/37bucM

clck.ru/37kVDZ

https://vk.com/verify

Дополнительные задания

Тема урока. ЕГЭ №2

Евгений Джобс, № 198 в сборнике Полякова

Если первый столбец будет у , то он равен 0 , а 3-й столбец будет w , тоже равен 0. А это совпадает с 3 строкой!

Значит 1-й равен w, а 3-й равен y.

w/y

w/y

print('x','y','z','w')

for x in range(2):

for y in range(2):

for z in range(2):

for w in range(2):

if (w

print(x,y,z,w)

https://youtu.be/Jic3hOvCwyM?t=525

Ответ: wzyx

Тема урока. ЕГЭ №2

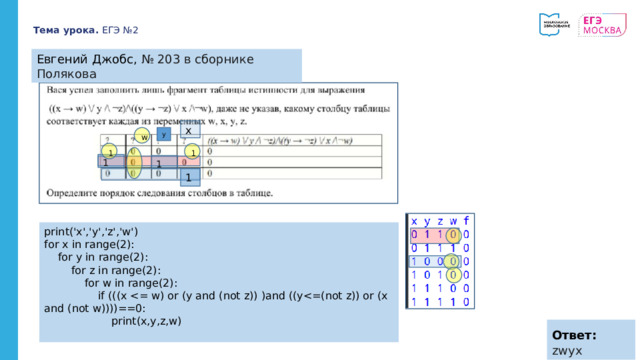
Евгений Джобс, № 203 в сборнике Полякова

x

y

w

1

1

1

1

1

print('x','y','z','w')

for x in range(2):

for y in range(2):

for z in range(2):

for w in range(2):

if (((x

print(x,y,z,w)

https://youtu.be/u7SWndsZS6Q?t=385

Ответ: zwyx

Тема урока. ЕГЭ №2

Задание

Составим таблицу истинности для выражения (¬ a ∧ ¬ b ) ∨ ( b ≡ c ) ∨ d и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах будем записывать переменные в порядке a, b, c, d . Получим следующие наборы:

(0, 1, 0, 0),

(1, 0, 1, 0),

(1, 1, 0, 0).

Заметим, что во всех наборах переменная d равна 0, следовательно, переменной d соответствует второй столбец, где нет единичных значений.

Заметим, что набору (0, 1, 0, 0) может соответствовать только первая строка таблицы, поскольку в других строках как минимум две переменные принимают единичное значение. Следовательно, третий столбец соответствует переменной b .

В третьей строке таблицы переменная b равна 1, следовательно, третья строка соответствует набору (1, 1, 0, 0), в котором единичное значение принимает также переменная a , тогда переменной a соответствует четвертый столбец, а переменной c  —  первый.

2 способ:

from itertools import *

for a, b, c, d in product([0, 1], repeat=4):

if not ((not a and not b) or (b == c) or d):

      print(a, b, c, d)

Программирование:

1 способ:

for a in range(2):

for b in range(2):

         for c in range(2):

for d in range(2):

                     if not ((not a and not b) or (b==c) or d):

print(a,b,c,d)

Ответ:

Тема урока. ЕГЭ №2

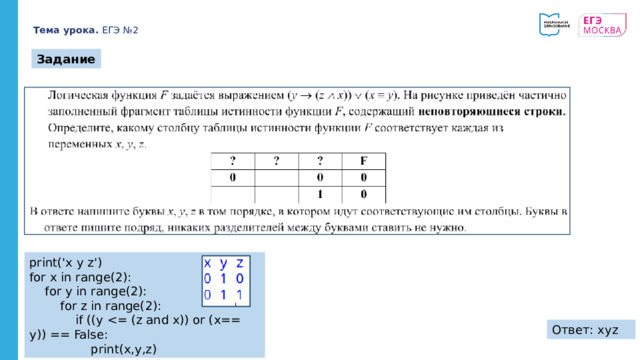
Задание

print('x y z')

for x in range(2):

for y in range(2):

for z in range(2):

if ((y

print(x,y,z)

Ответ: xyz

Тема урока. ЕГЭ №2

Задание:

Ответ: cdba.

Тема урока. ЕГЭ №2

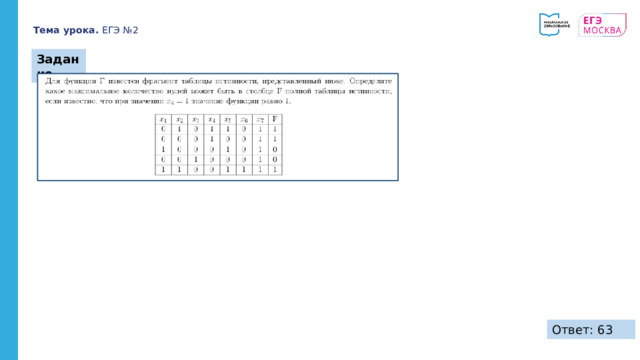
Задание

Ответ: 63

Тема урока. ЕГЭ №2

Задание

Ответ: abcd

Тема урока. ЕГЭ №2

Задание

print('x','y','z','w')

for x in range(2):

for y in range(2):

for z in range(2):

for w in range(2):

if ((x

print(x,y,z,w,1)

Логическая функция  F  задаётся выражением ( x   →   y ) ∧ ( y  ≡ ¬ z ) ∧ ( z   ∨   w ).

Ниже приведён частично заполненный фрагмент таблицы истинности функции  F , содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции  F  соответствует каждая из переменных  x ,  y ,  z ,  w .

Впишите эти переменные в соответствующие ячейки таблицы.

?

?

1

?

1

?

1

1

F

1

1

1

1

1

Ответ:

Тема урока. ЕГЭ №2

Крылов. ЕГЭ-2023 Вариант №17

Ответ:

Тема урока. ЕГЭ №2

Задание

Ответ: