Урок 96 – 98.
Подготовка к ЕГЭ.
Цели урока: решить полностью вариант ЕГЭ для освоения и ориентации в заданиях.
Ход урока.
1. Организационный момент.
2. Задания с выбором ответа А1 – А13.
Часть 1.
А1. Найдите значение выражения 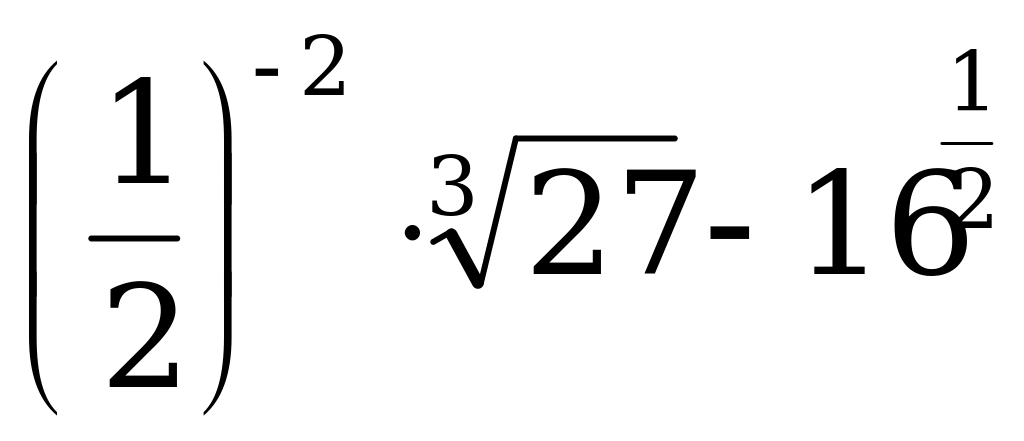 .
.
1) 0; 2) 2; 3) 4; 4) 8.
Решение:
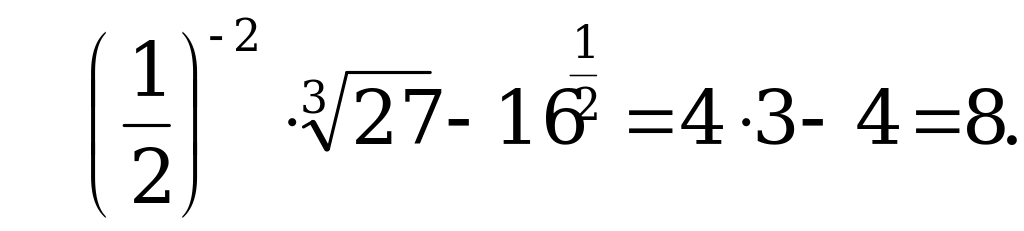
Ответ: 4.
А2. Упростите выражения 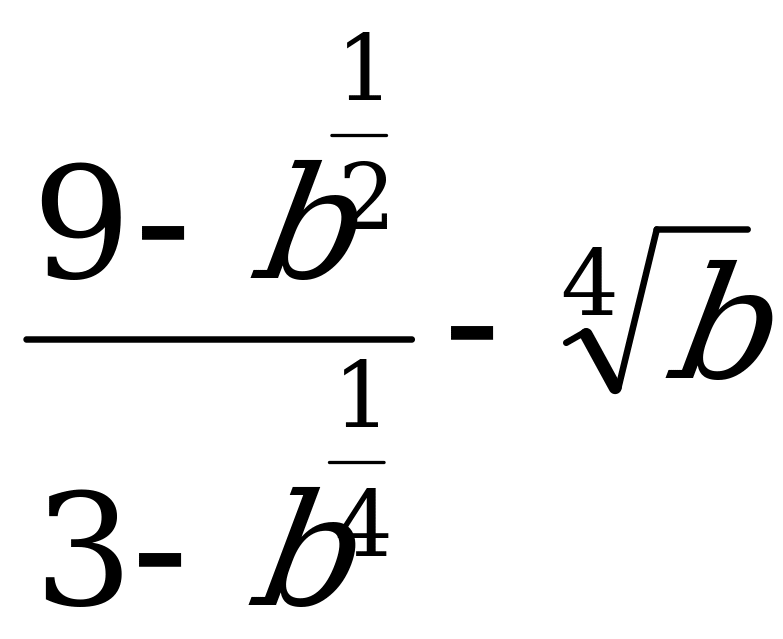 .
.
1) 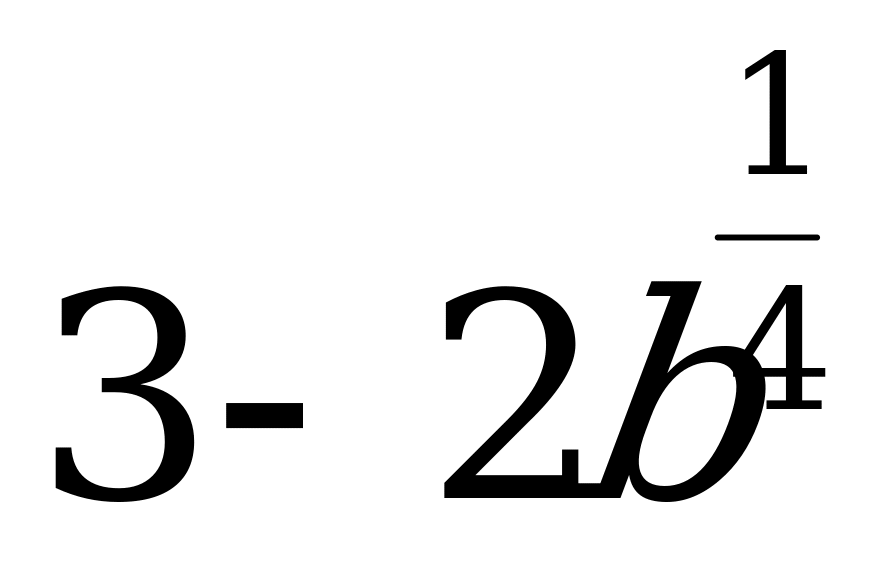 ; 2) 3; 3) 0; 4)
; 2) 3; 3) 0; 4) 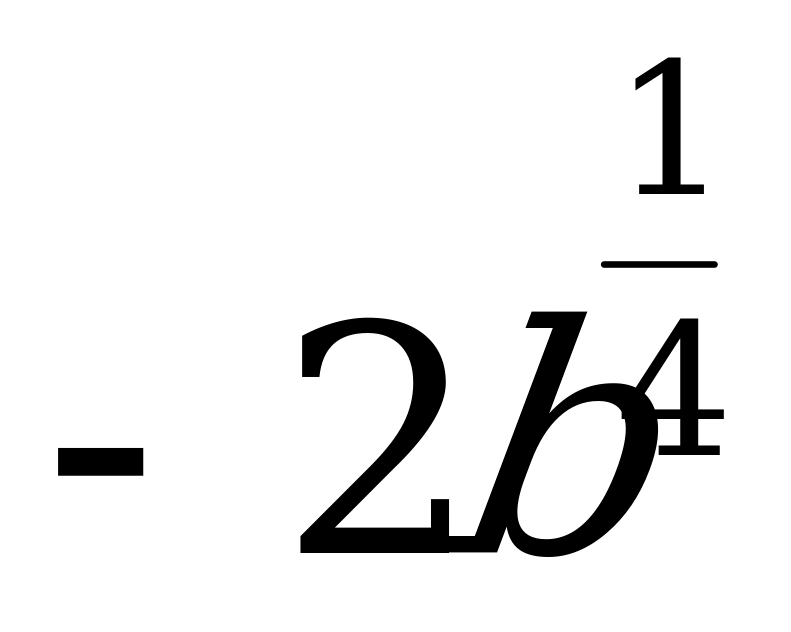 .
.
Решение:
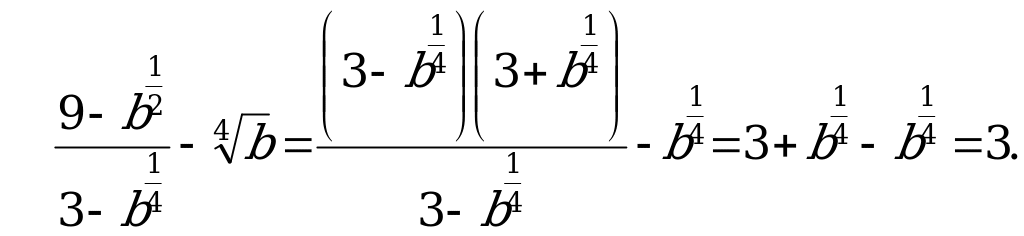
Ответ: 2.
А3. Упростите выражения 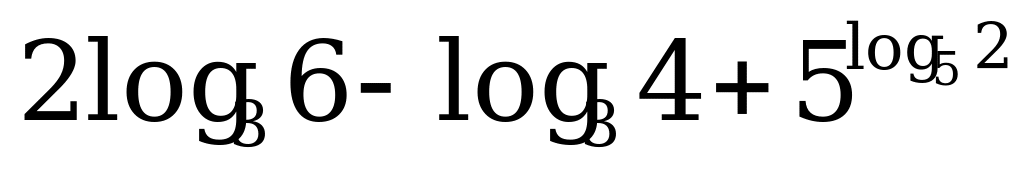 .
.
1) 0; 2) 13; 3) 7; 4) 4.
Решение:
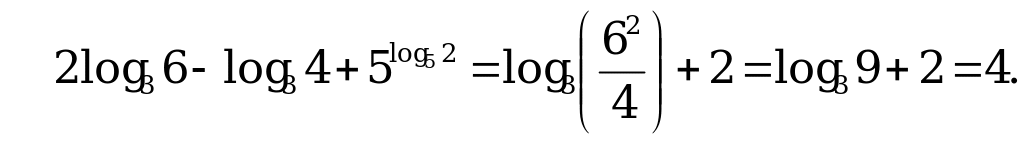
Ответ: 4.
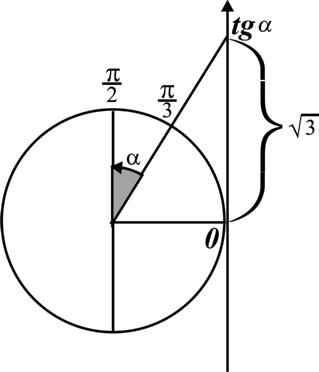
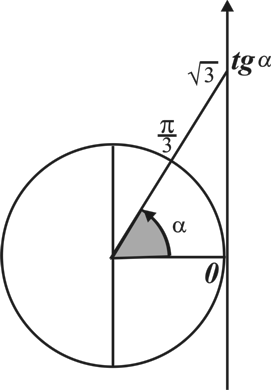
А4. Решите неравенство 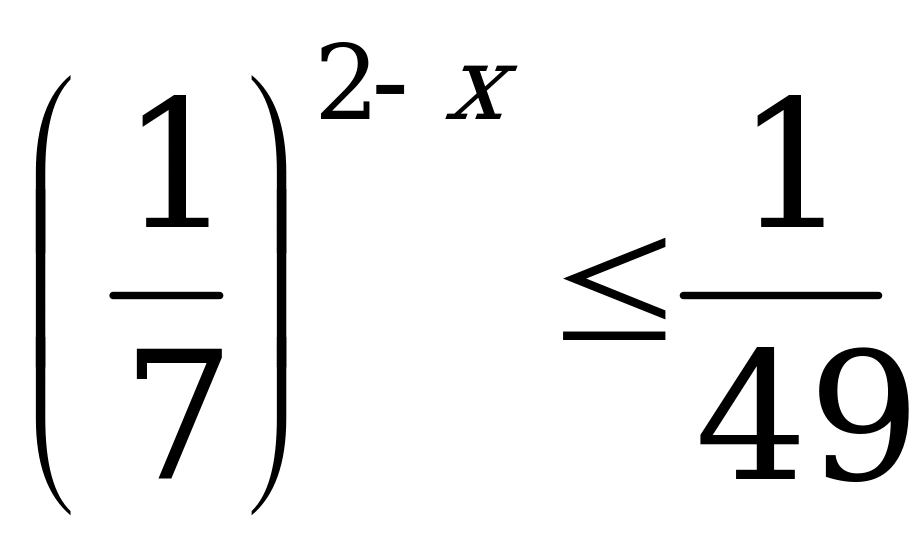 .
.
1) 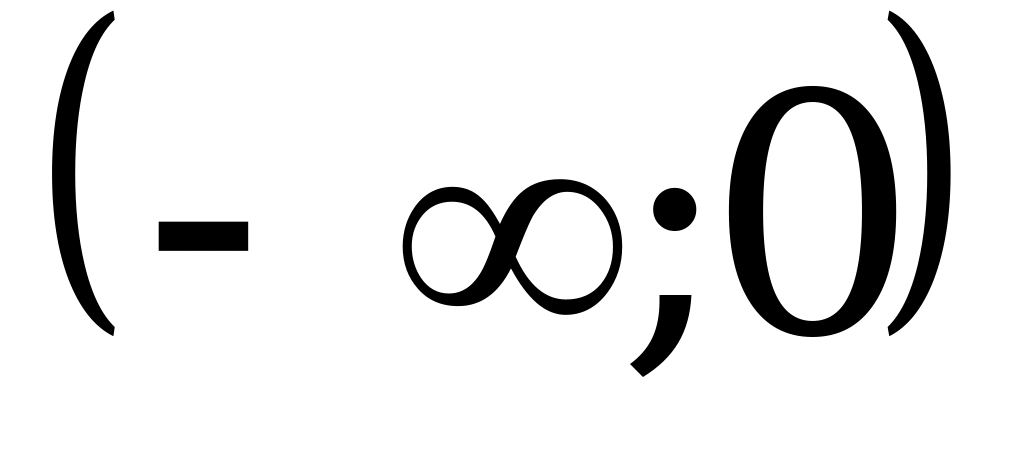 ; 2)
; 2) 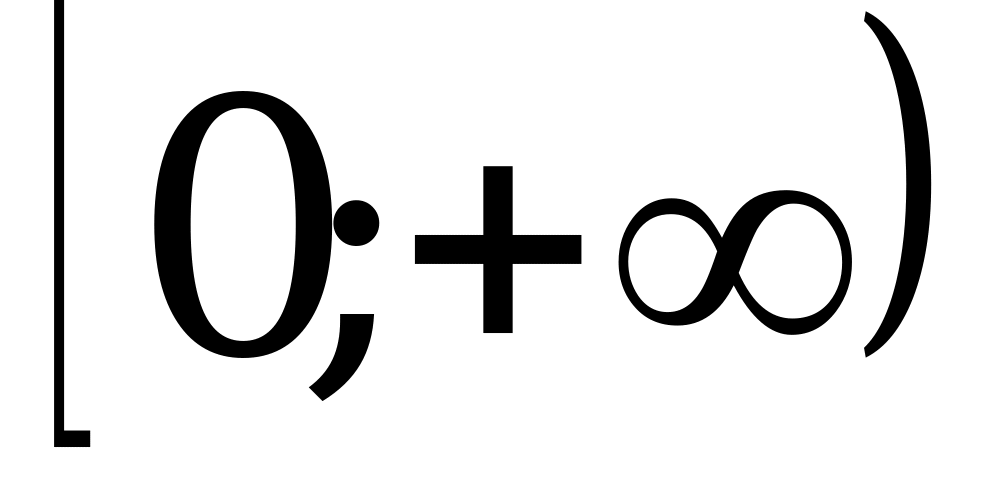 ; 3)
; 3) 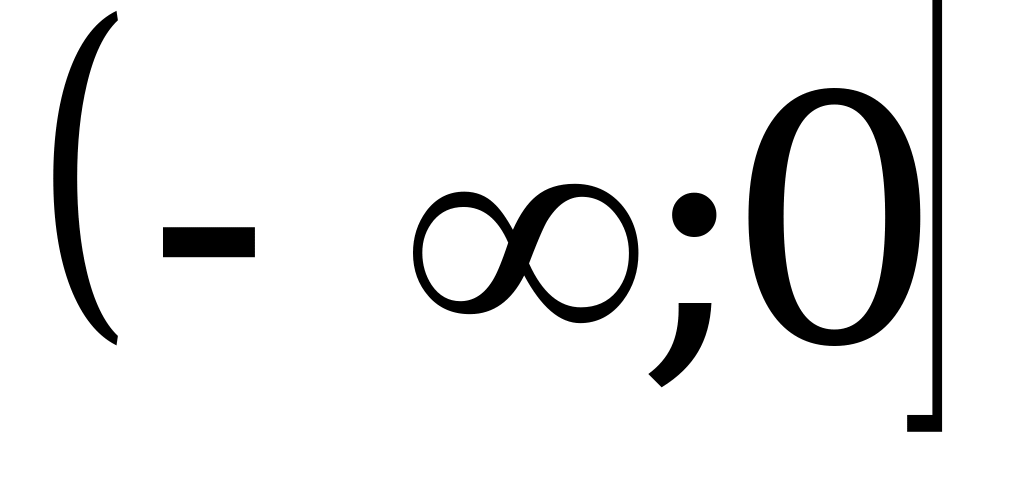 ; 4)
; 4) 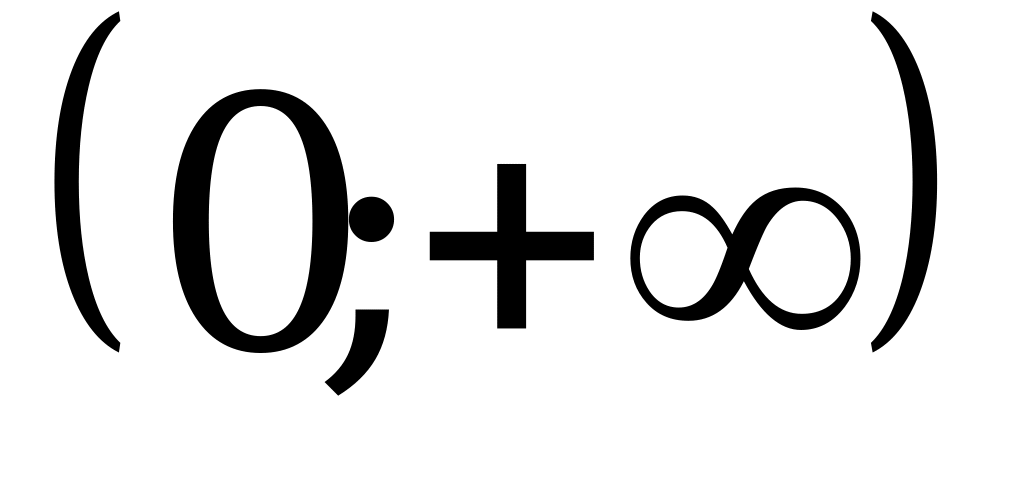 .
.
Решение:
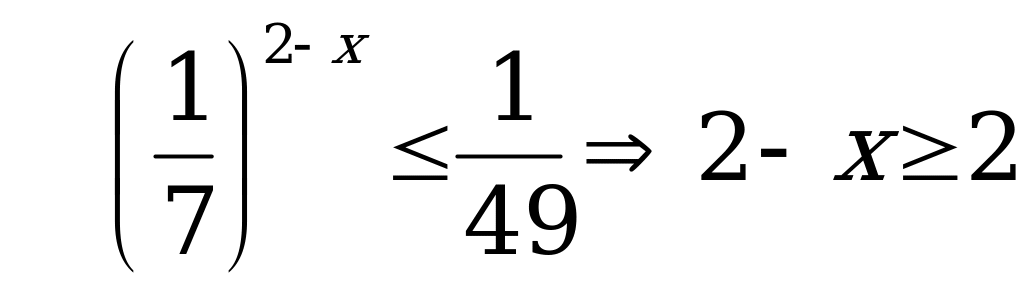 , так как
, так как 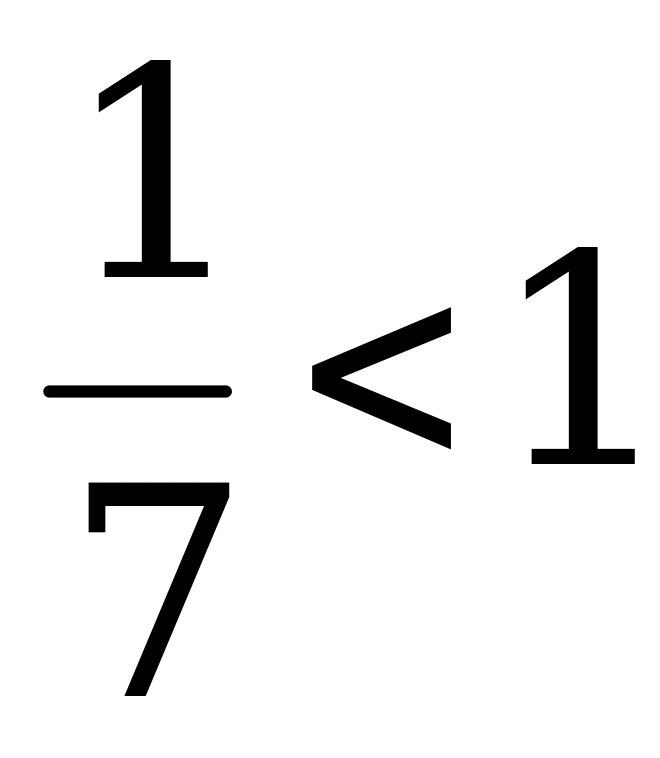 .
.
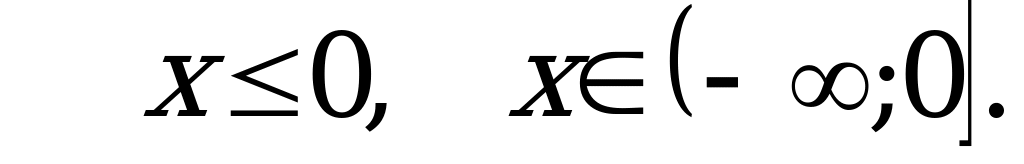
Ответ: 3.
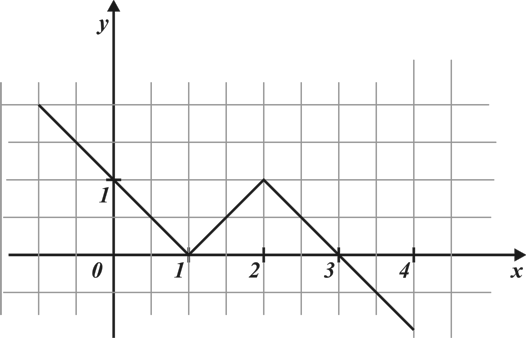
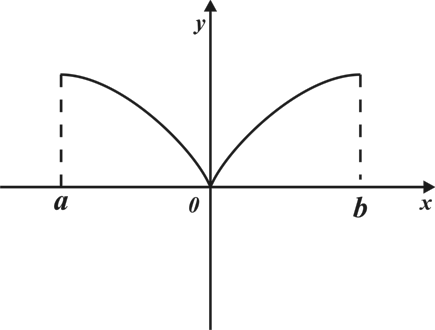
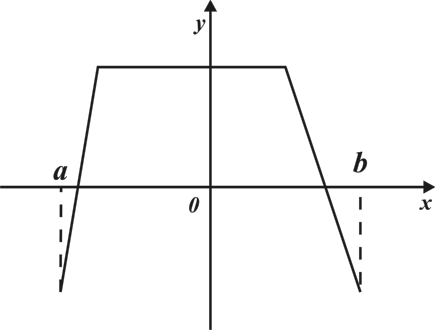
А5. Укажите промежуток возрастания функции 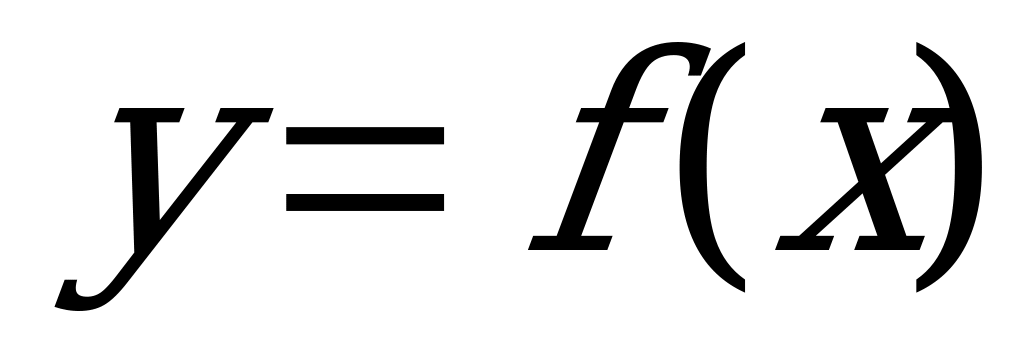 заданной графиком
заданной графиком
1) 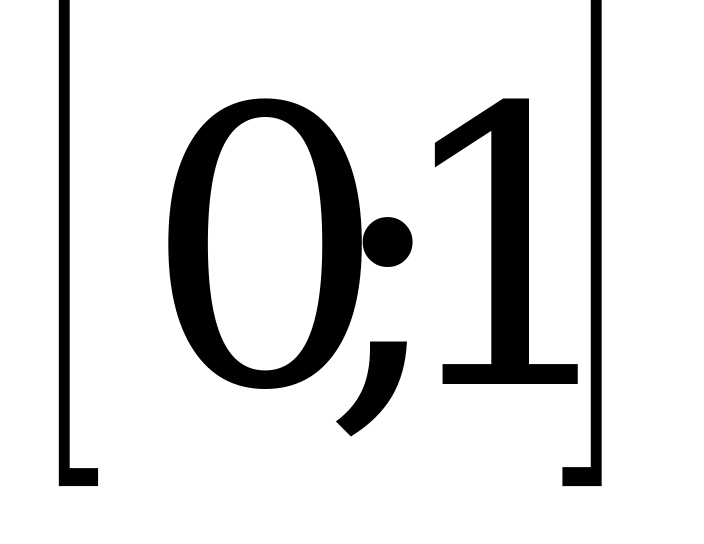 ; 2)
; 2) 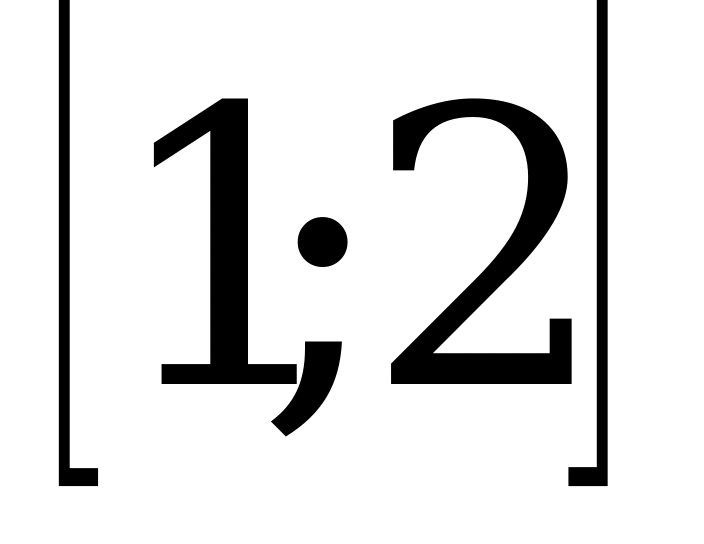 ; 3)
; 3) 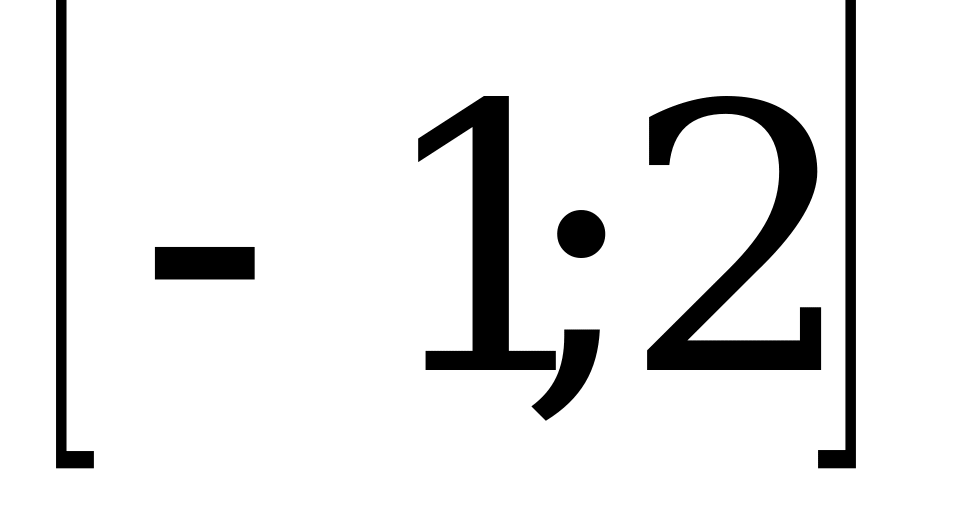 ; 4)
; 4) 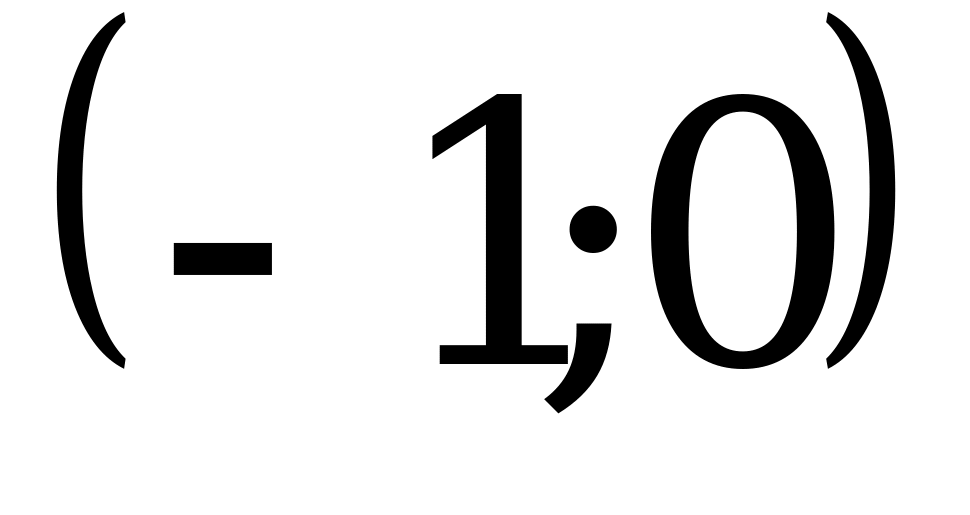 .
.
Решение:
Промежуток возрастания 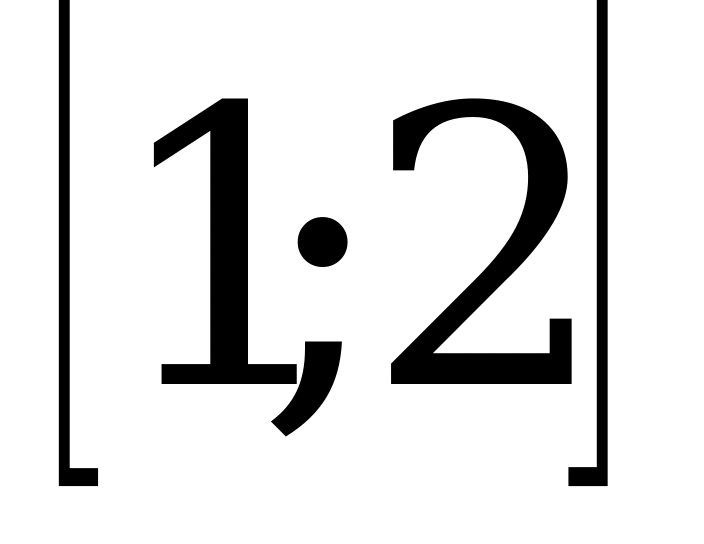 .
.
Ответ: 2.
А6. Упростите выражения 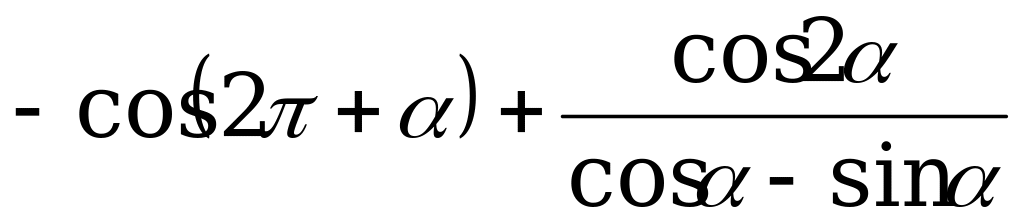 .
.
1) 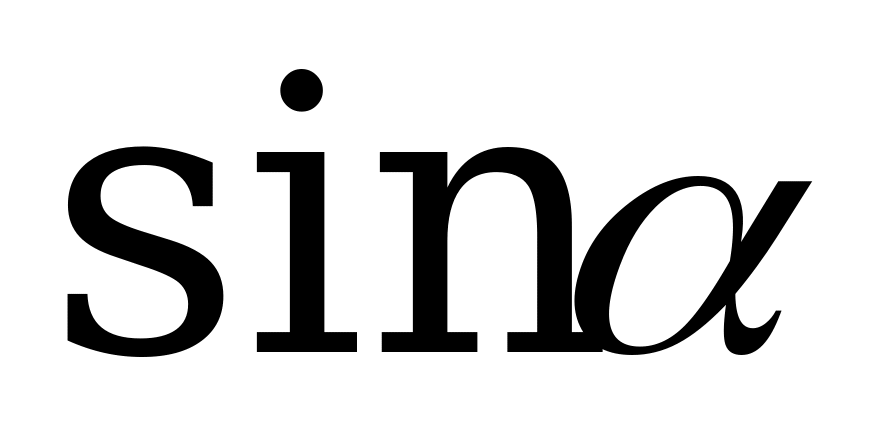 ; 2)
; 2)  ; 3)
; 3) 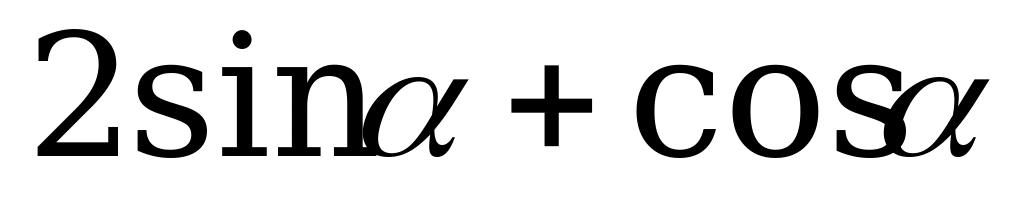 ; 4)
; 4) 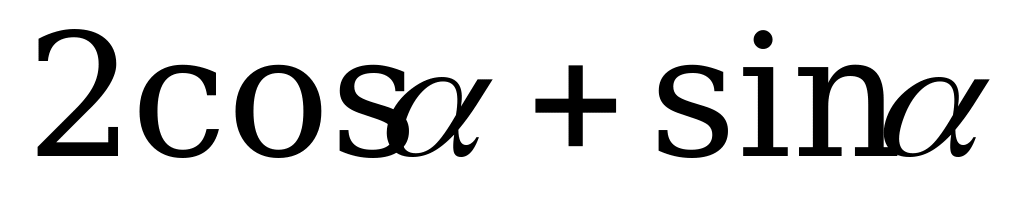 .
.
Решение:
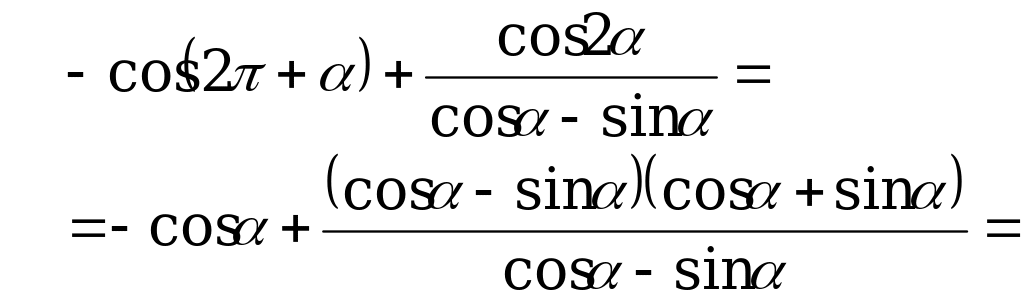

Ответ: 1.
А7. Найдите производную функции 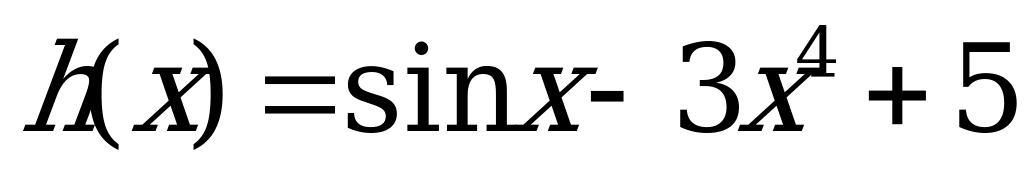 .
.
1) 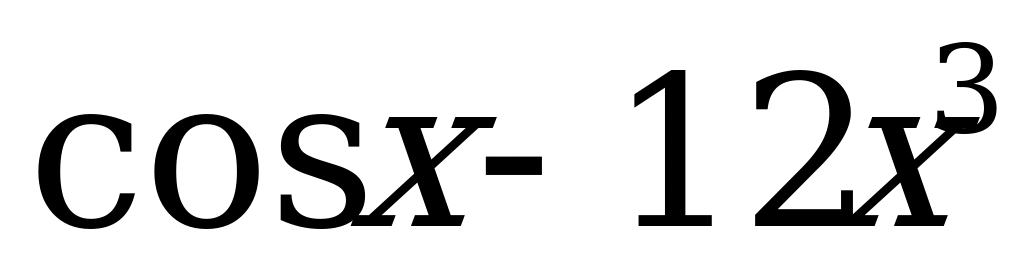 ; 2)
; 2) 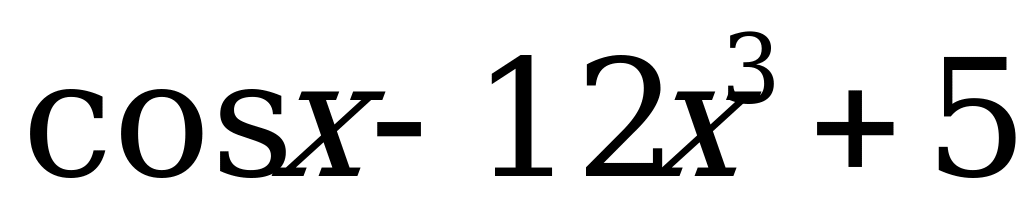 ;
;
3) 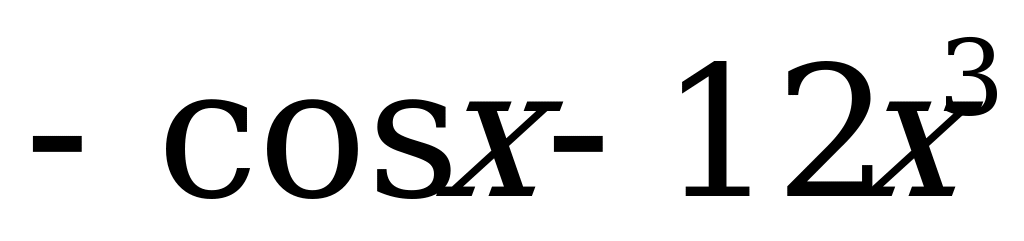 ; 4)
; 4) 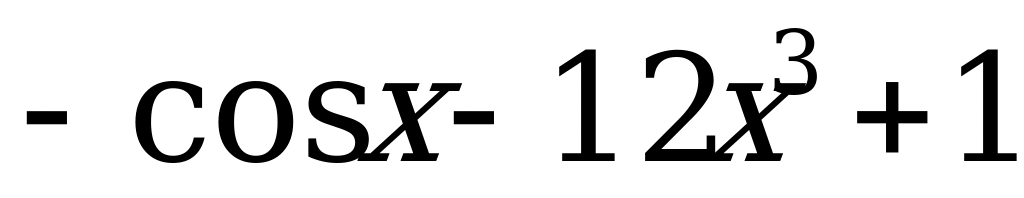 .
.
Решение:
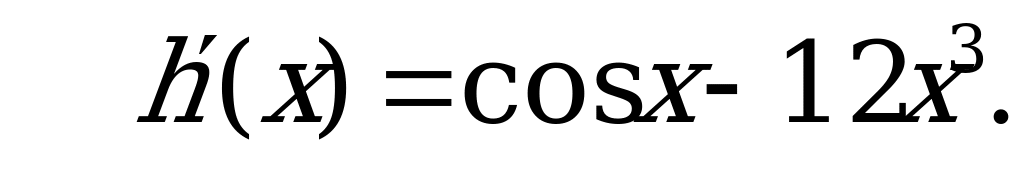
Ответ: 1.
А8. Укажите промежуток, которому принадлежит корень уравнения 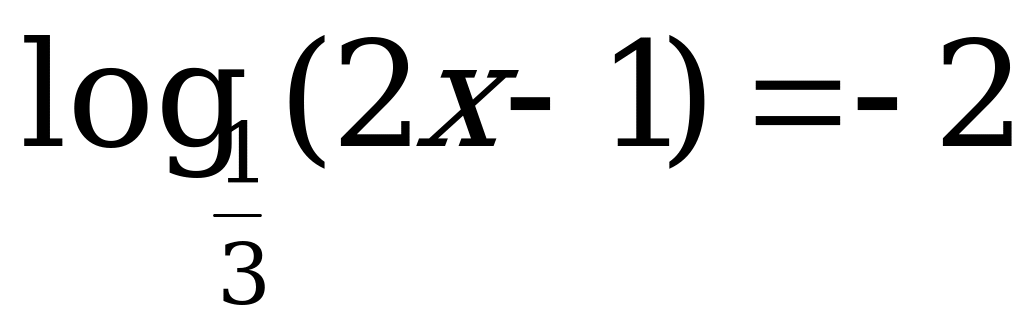 .
.
1) 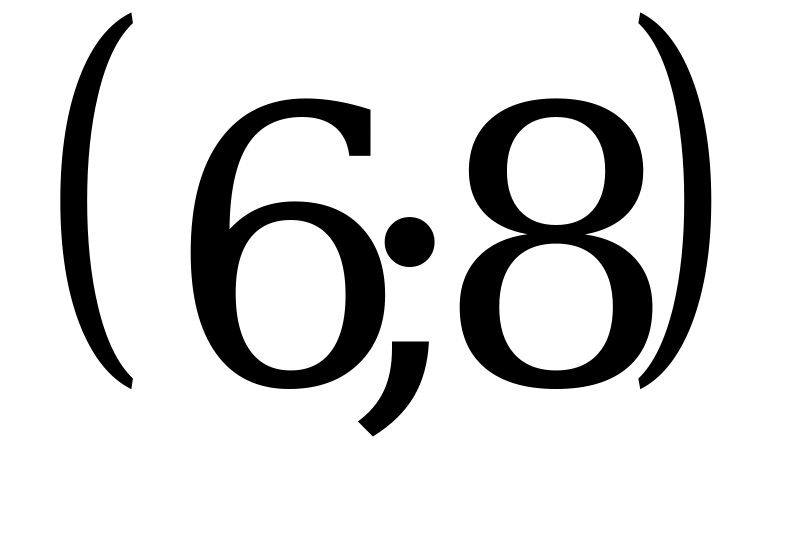 ; 2)
; 2) 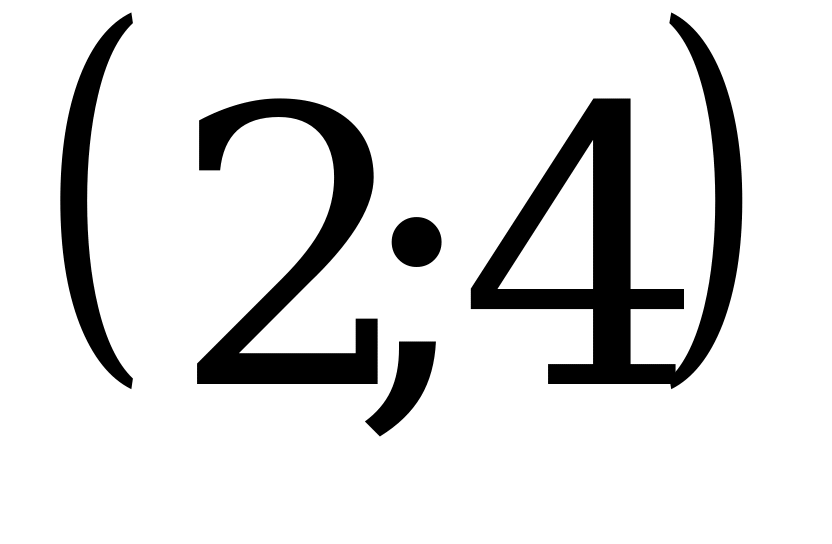 ; 3)
; 3) 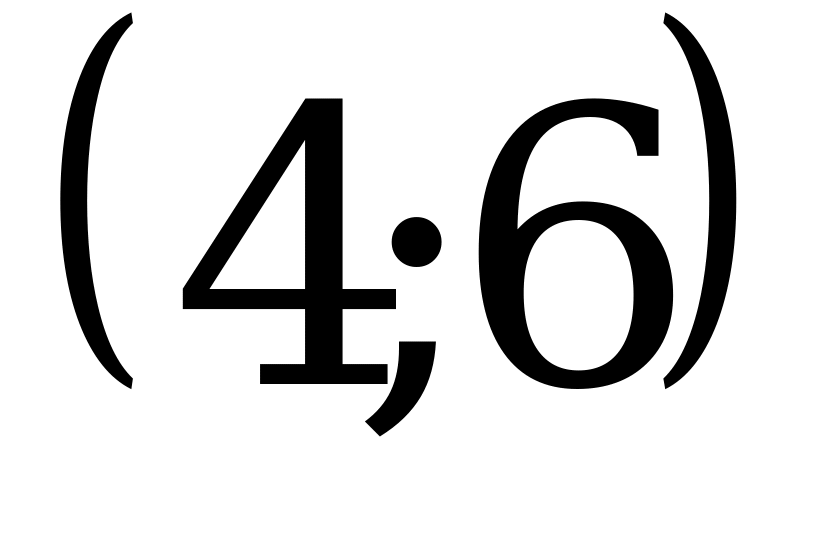 ; 4)
; 4) 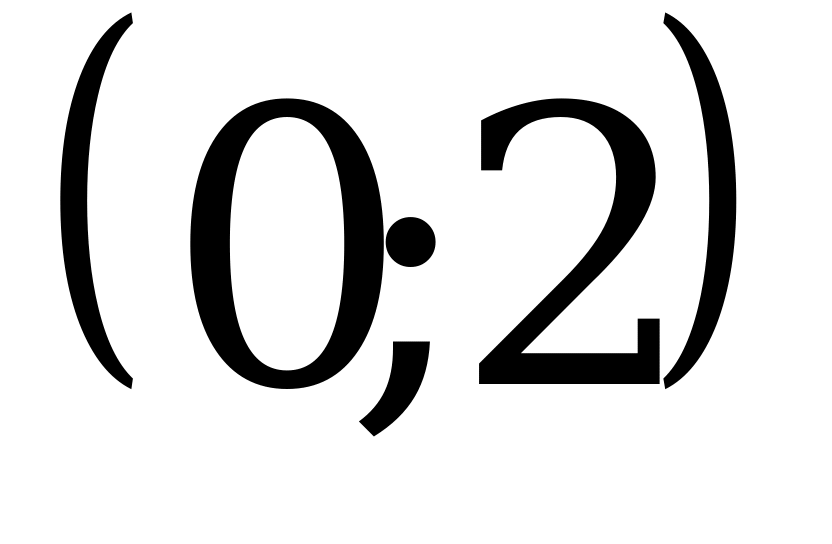 .
.
Решение:
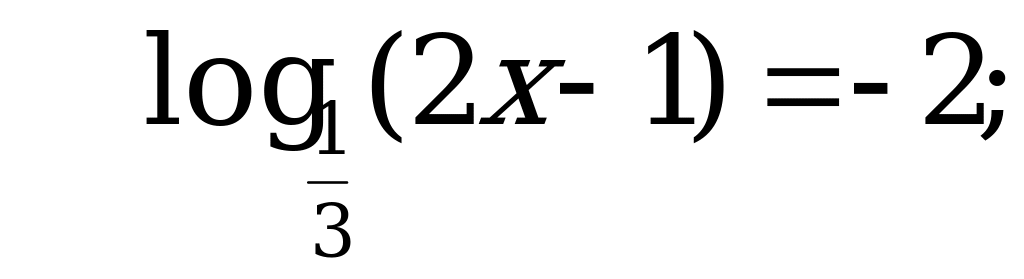
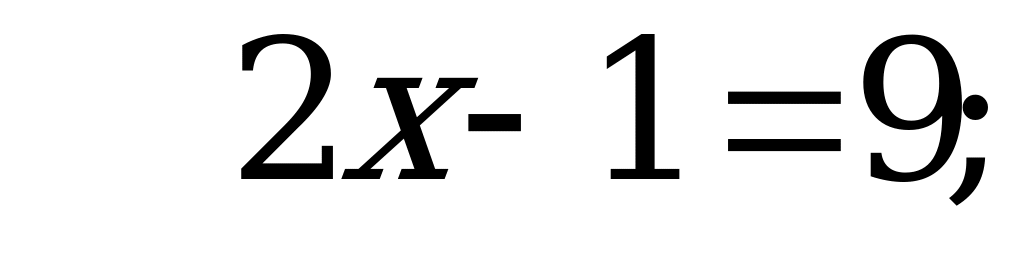
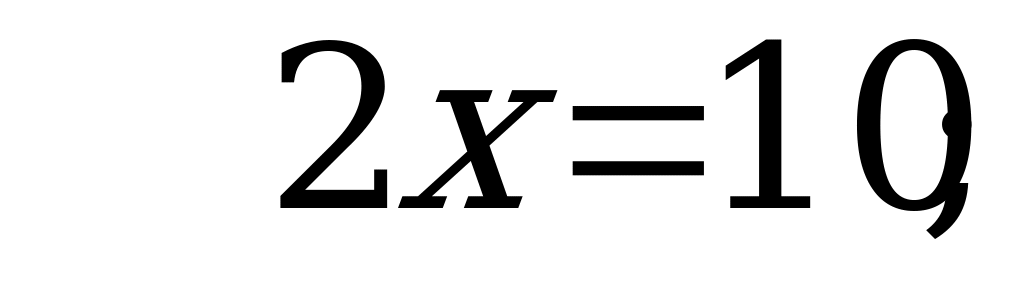
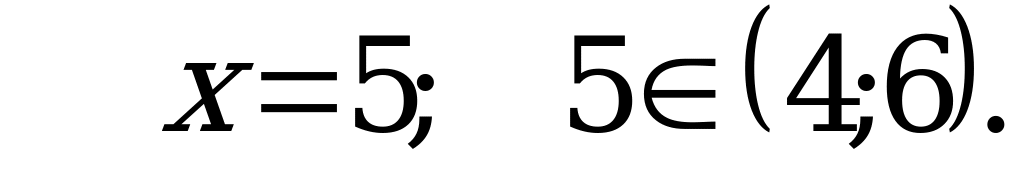
Ответ: 3.
А9. Найдите область определения функции 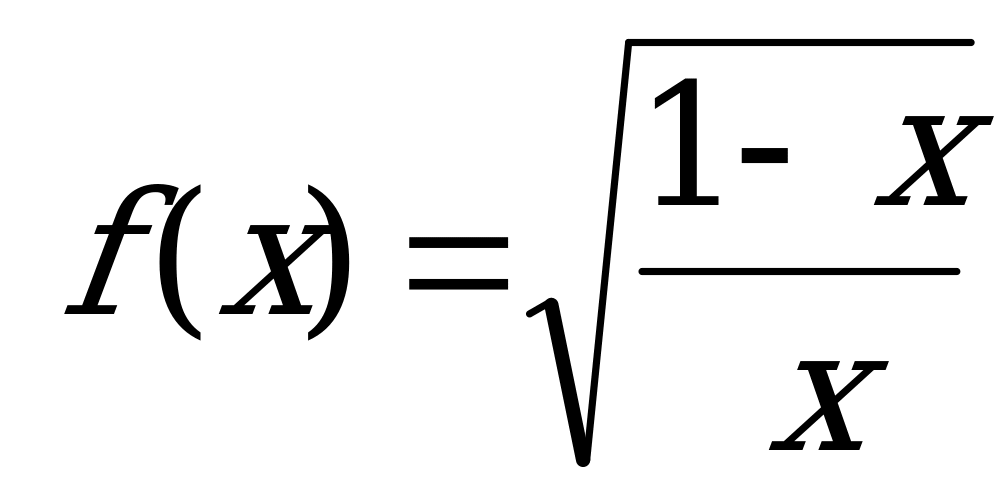 .
.
1) 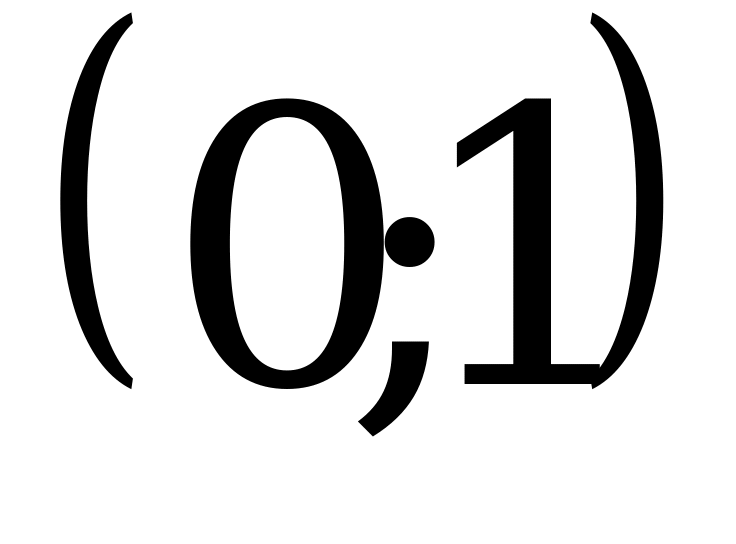 ; 2)
; 2) 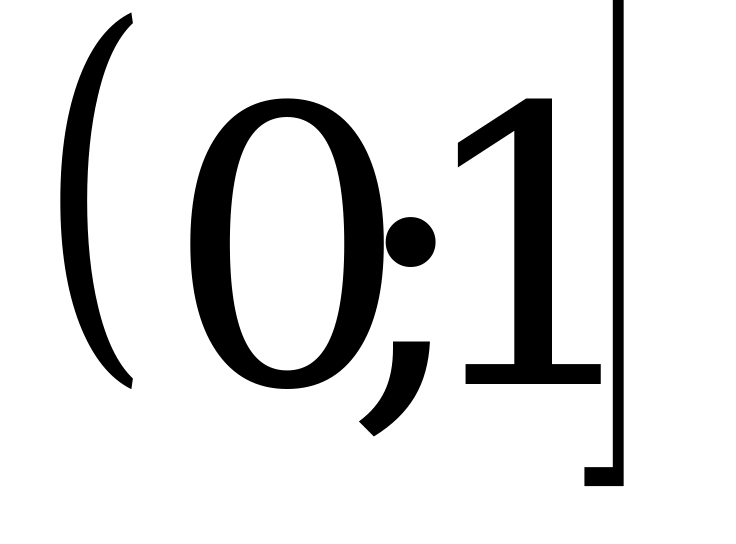 ;
;
3) 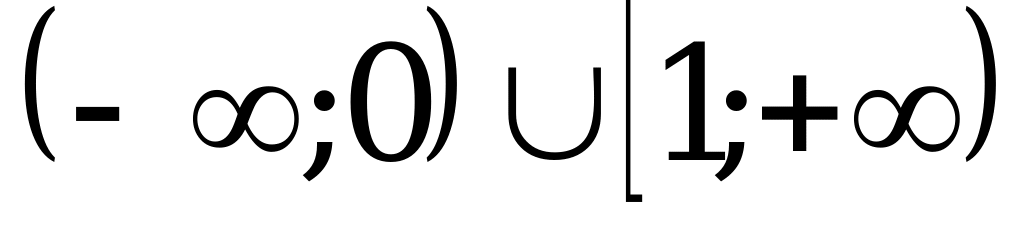 ; 4)
; 4) 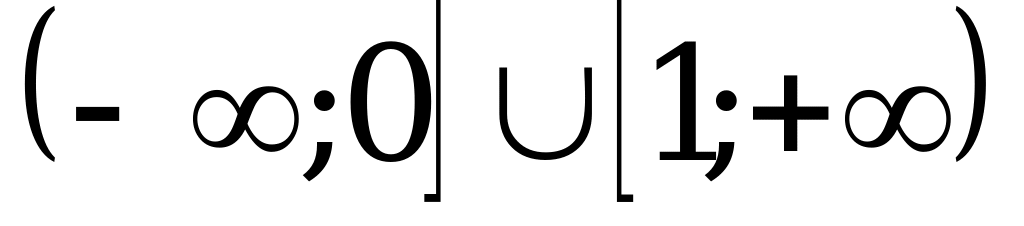 .
.
Решение:
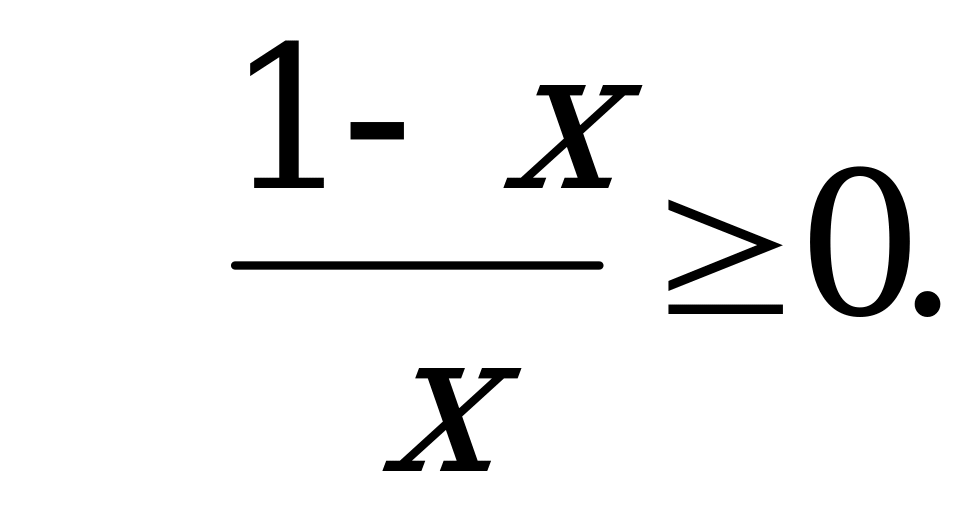
Нуль функции 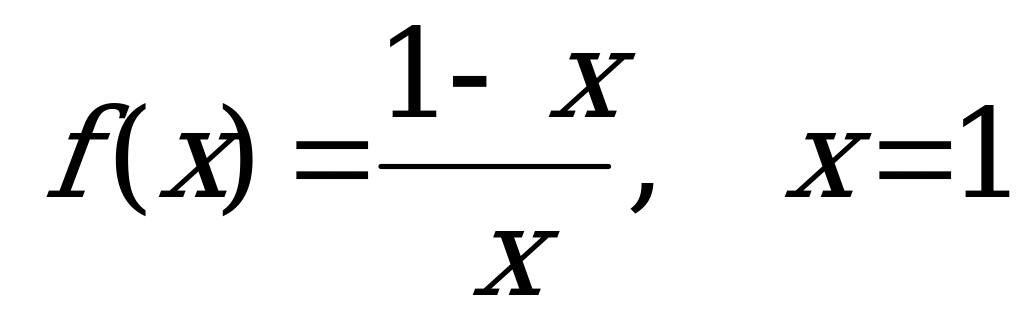 . При
. При 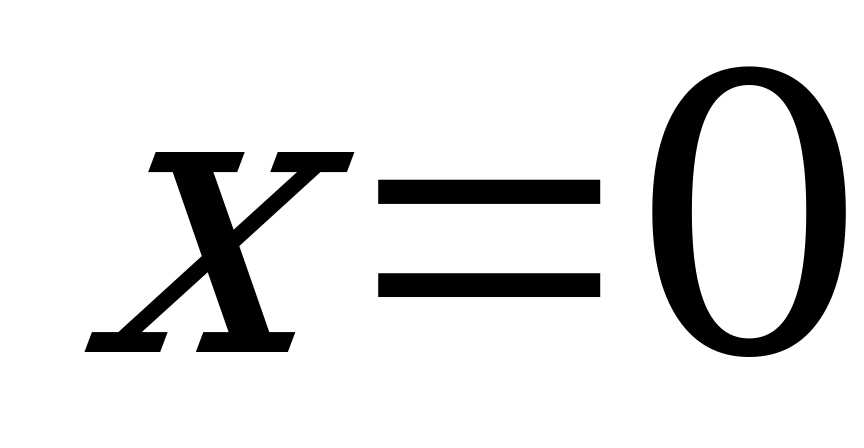 функция не существует. Отметим на координатной прямой данные значения
функция не существует. Отметим на координатной прямой данные значения 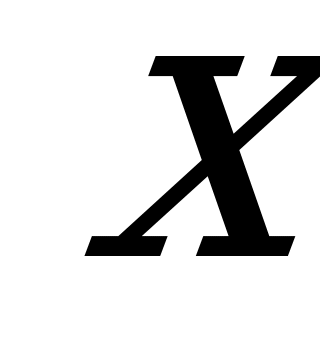 .
.
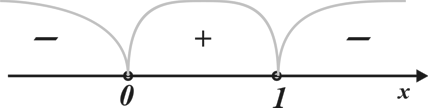

Ответ: 2.
А10. Найдите значение производной функции 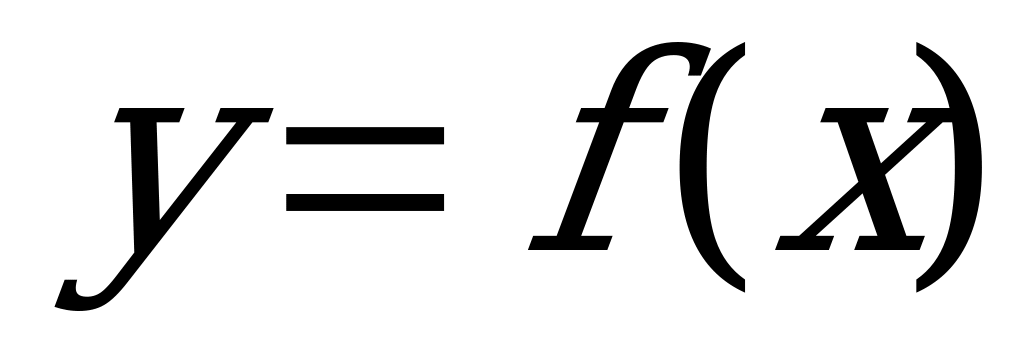 в точке
в точке 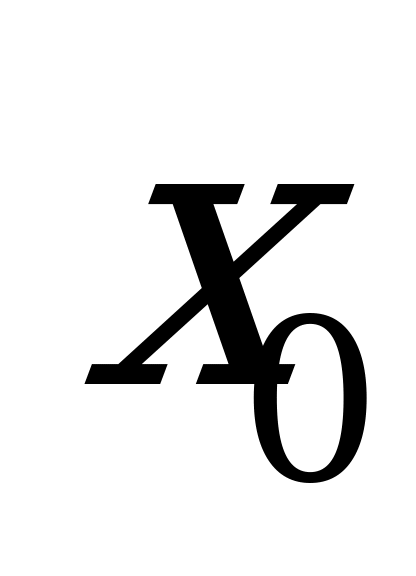 .
.
1) – 2; 2) 2; 3) – 1; 4) 1.
Решение:
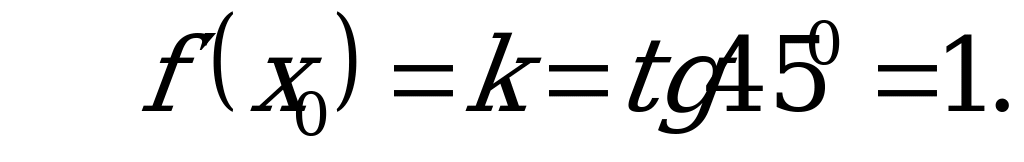
Ответ: 4.
А11. Найдите наибольшее значение функции 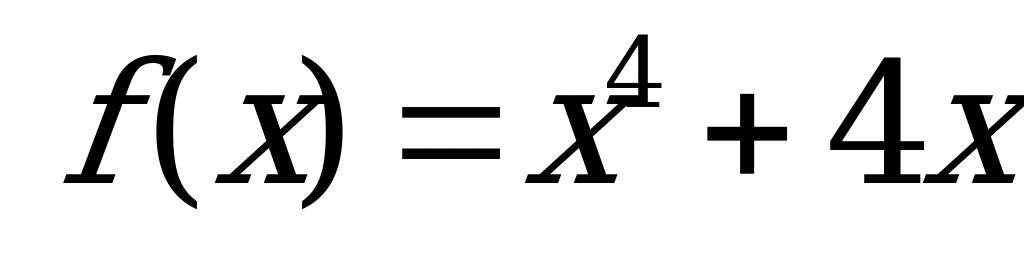 на отрезке
на отрезке 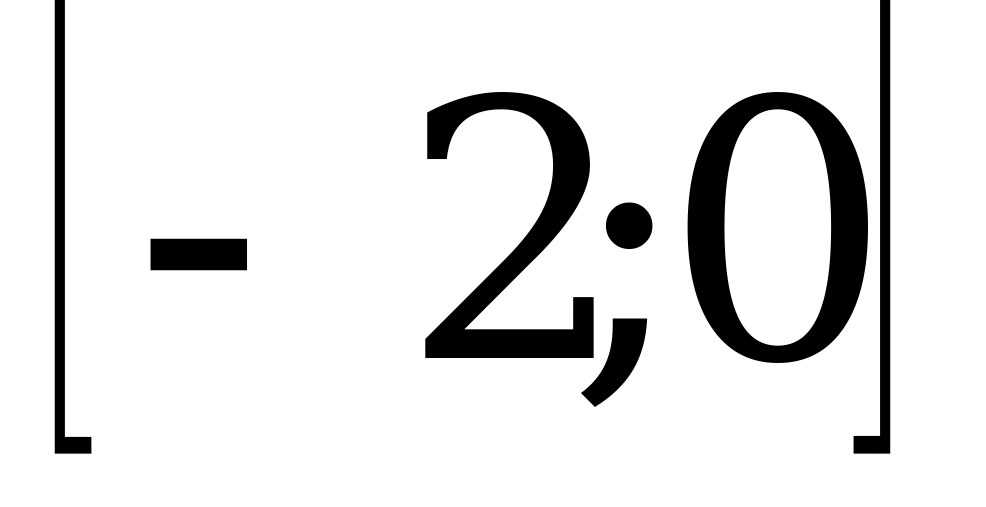 .
.
1) – 3; 2) 3; 3) 5; 4) 8.
Решение:
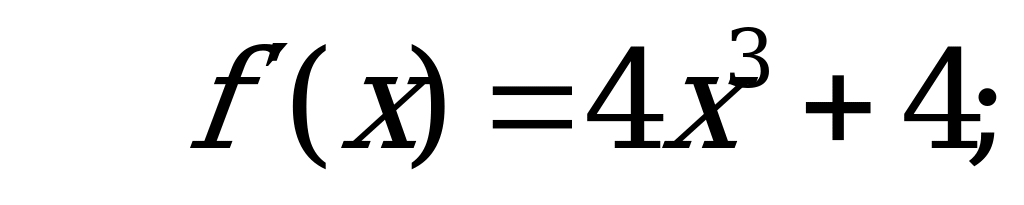
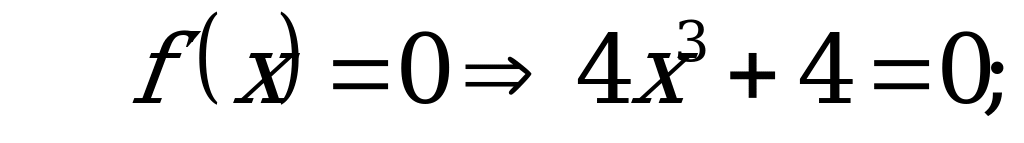
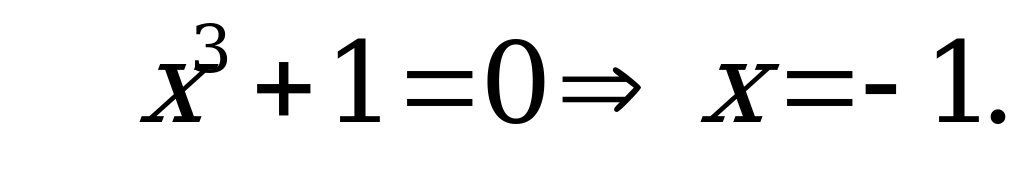
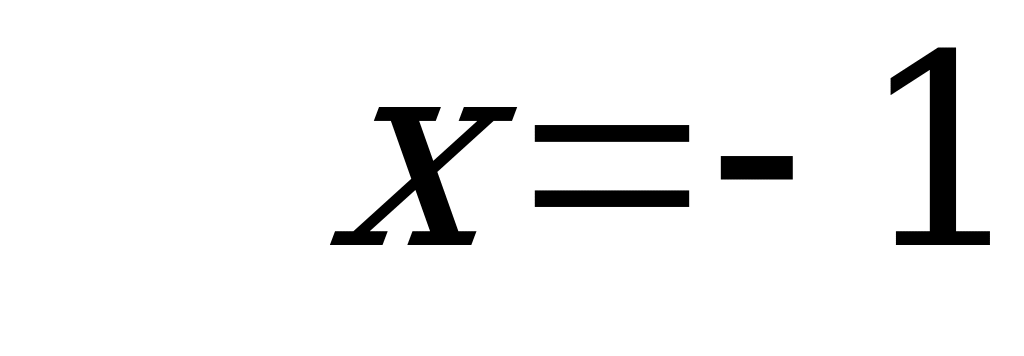 – критическая точка,
– критическая точка, 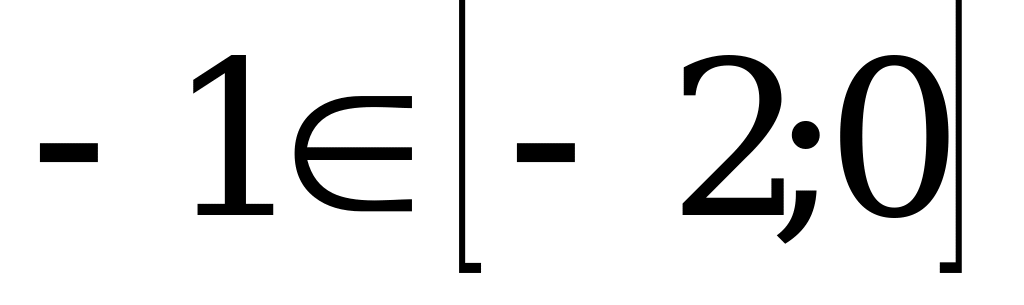 .
.
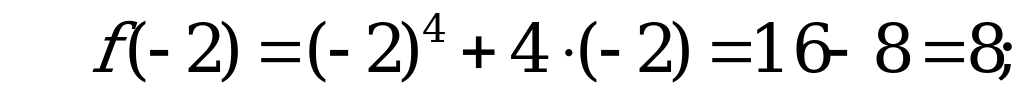
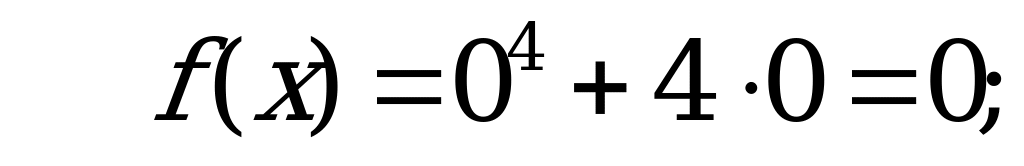
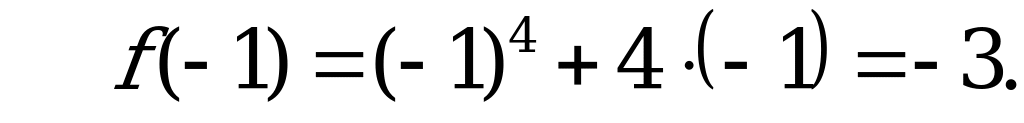
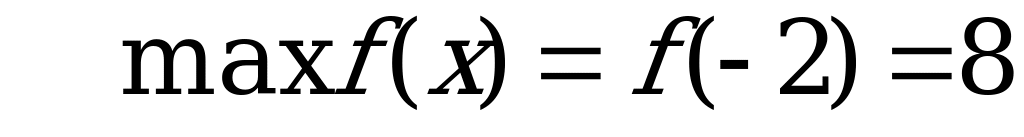 , где
, где 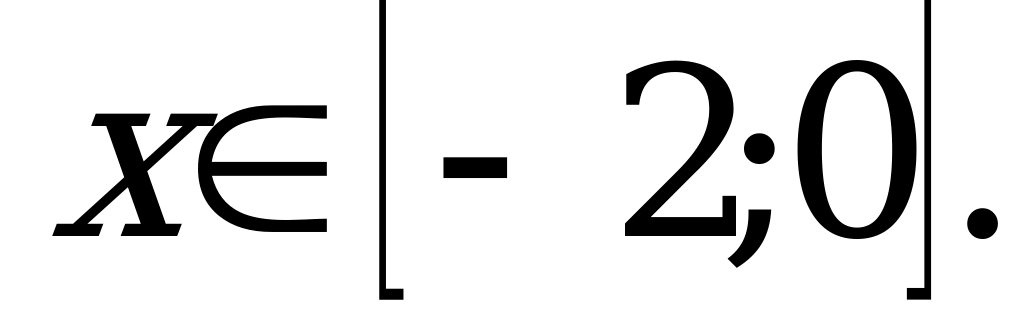
Ответ: 4.
А12. Найдите площадь фигуры, ограниченной линиями  .
.
1) 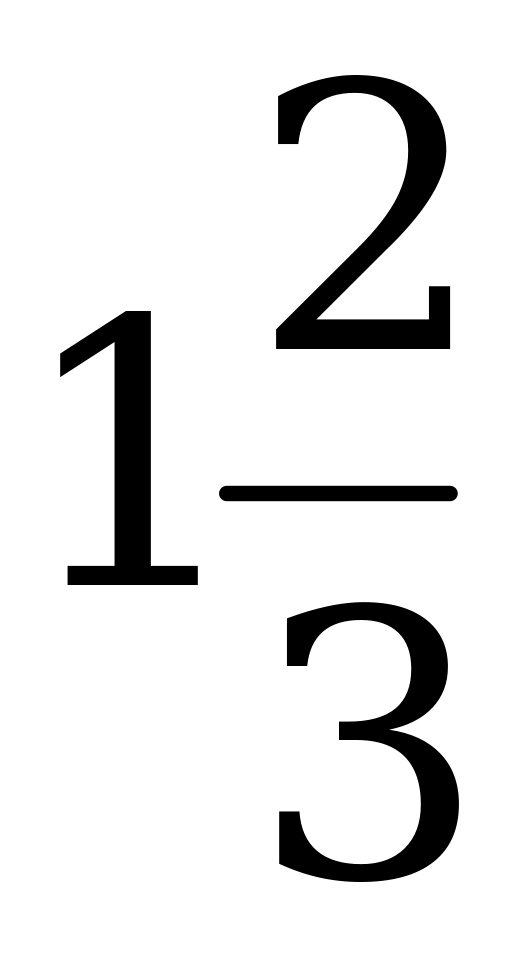 ; 2)
; 2) 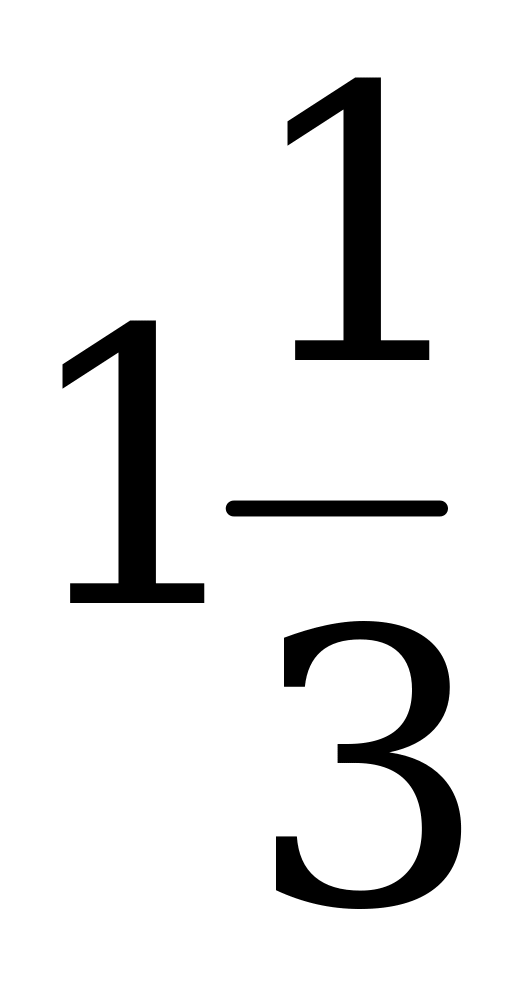 ; 3)
; 3) 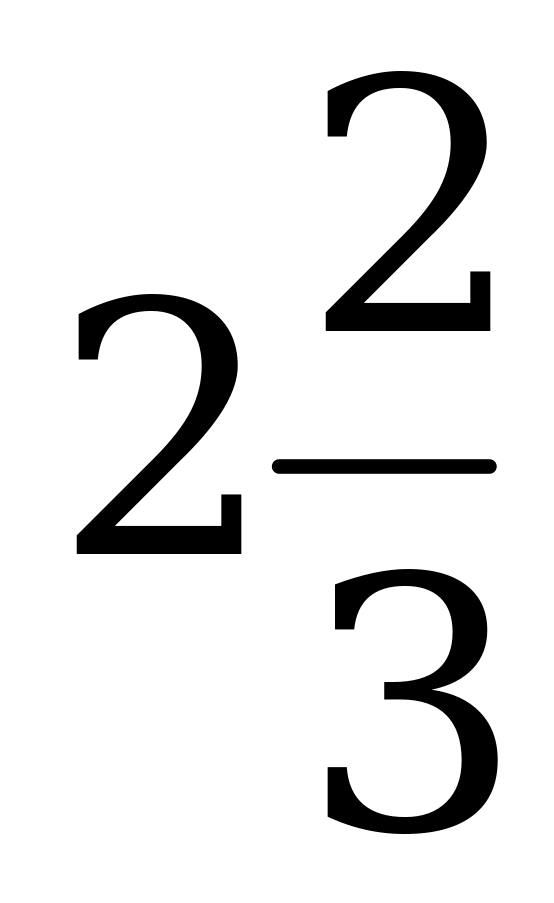 ; 4)
; 4) 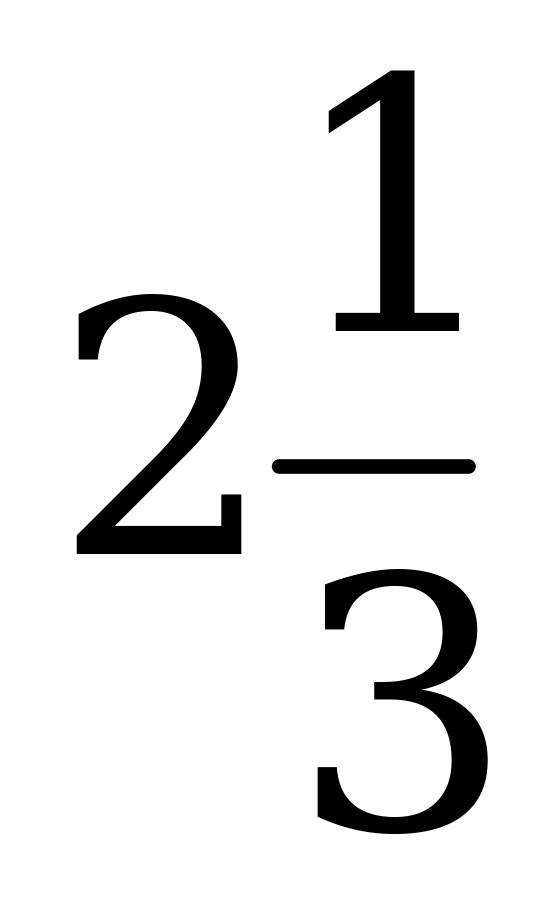 .
.
Решение:
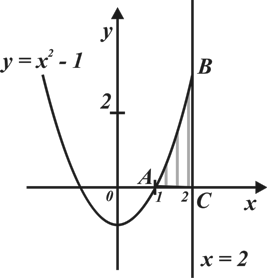
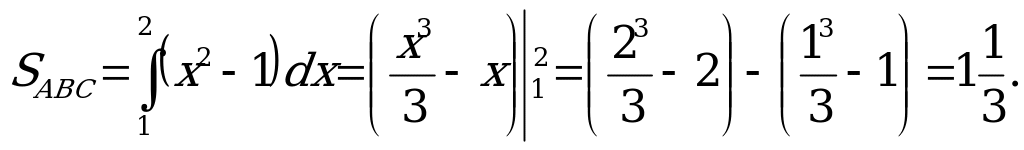
Ответ: 2.
А13. Решите уравнение 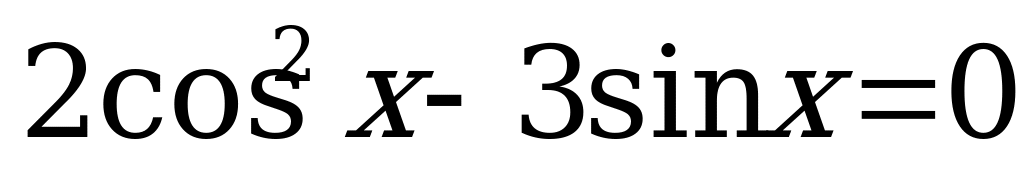 .
.
1) 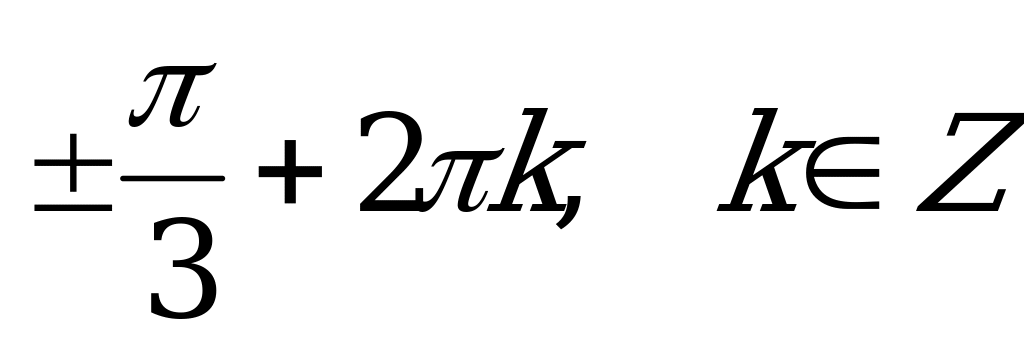 ; 2)
; 2) 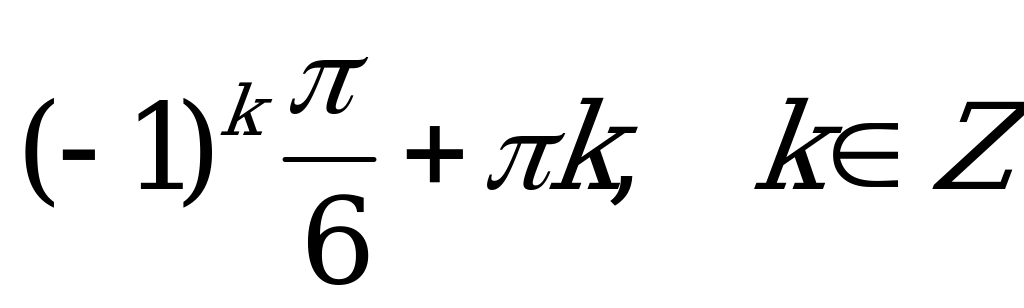 ;
;
3) 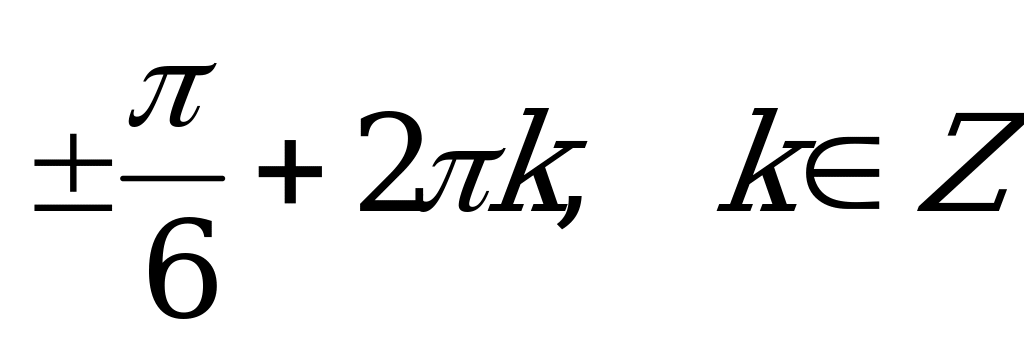 ; 4)
; 4) 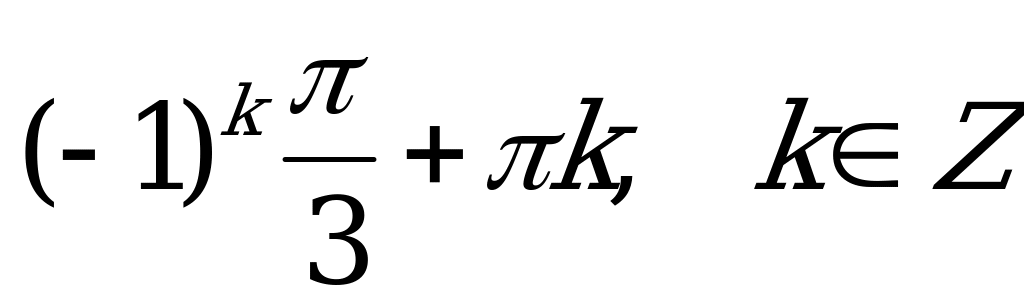 .
.
Решение:
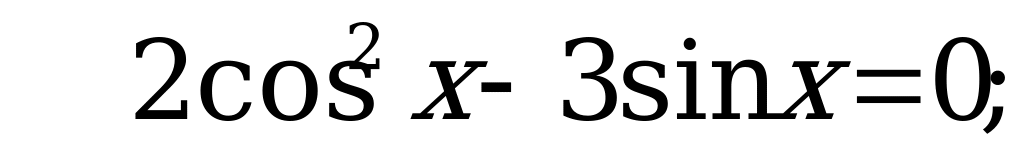
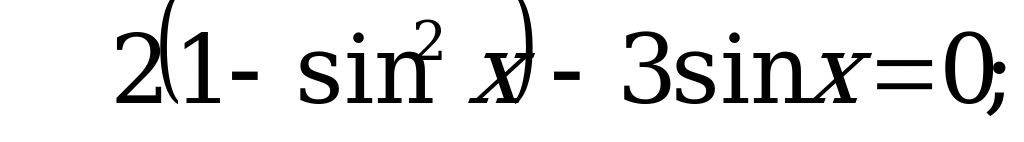
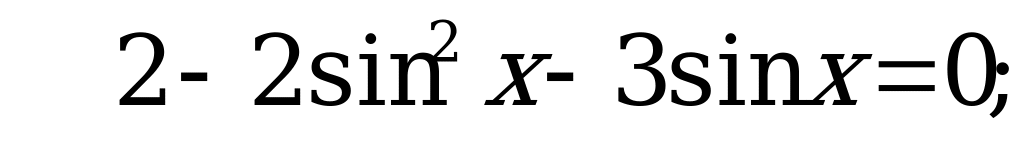
Пусть 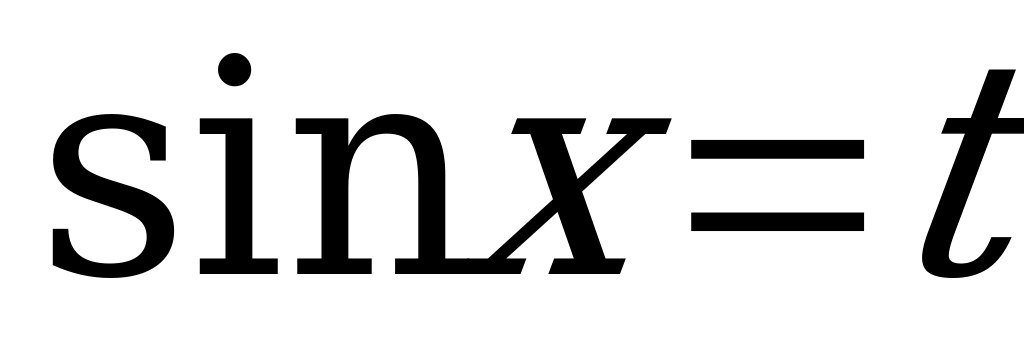 , тогда
, тогда
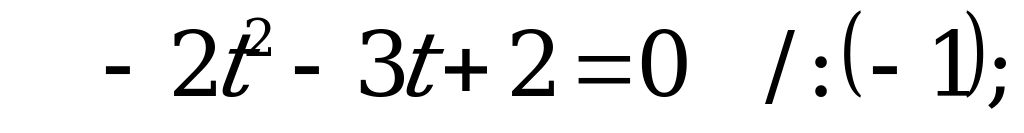
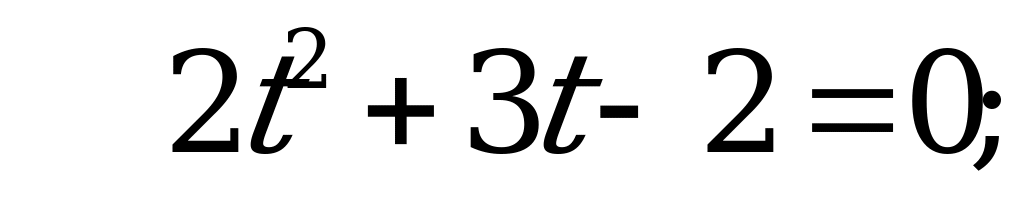
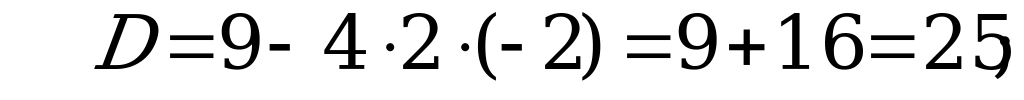
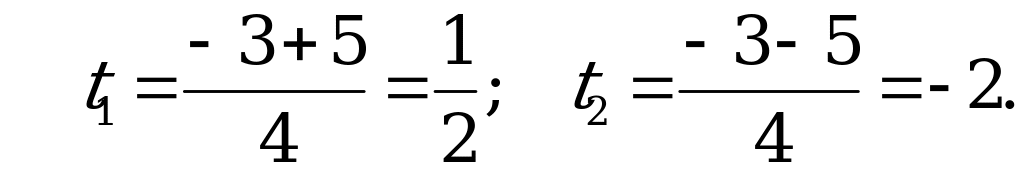
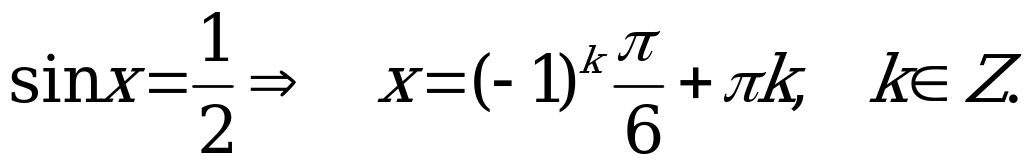
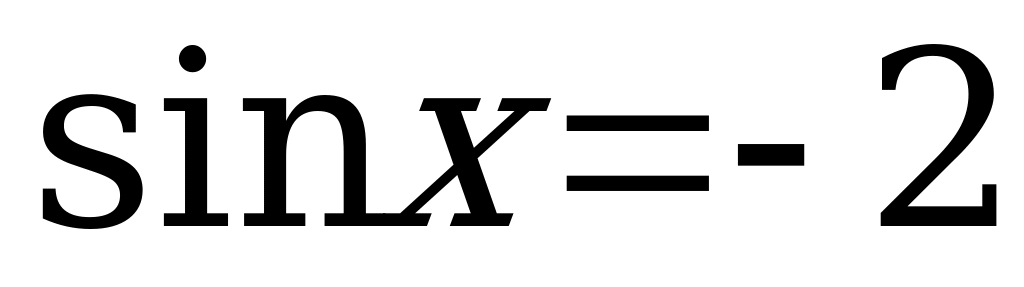 – нет корней.
– нет корней.
Ответ: 2.
3. Задание с кратким ответом В1 – В9.
Часть 2.
В1. Решите уравнение 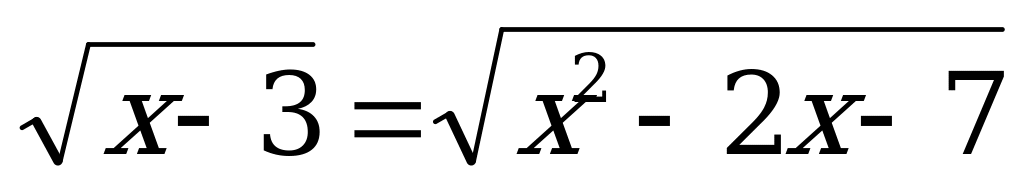 .
.
Решение:
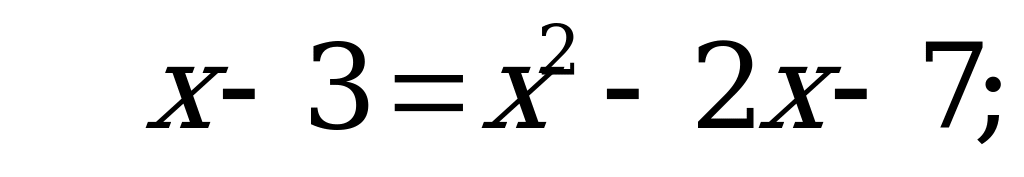
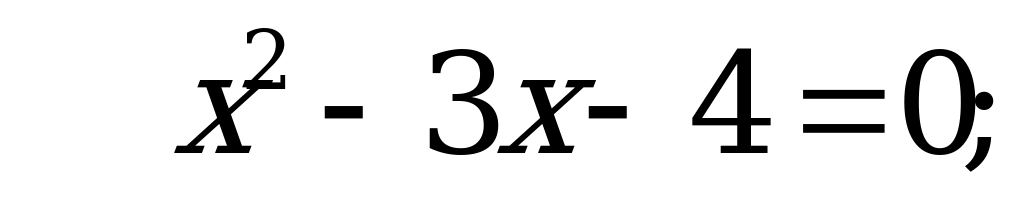
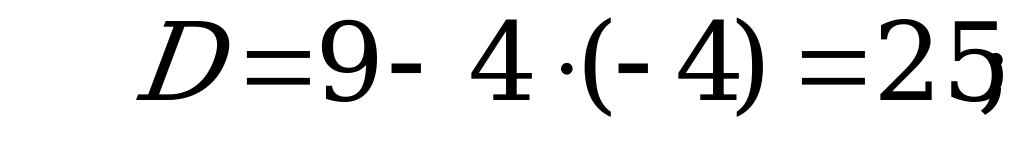
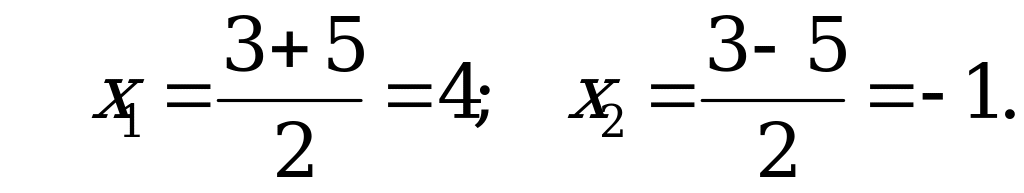
Если 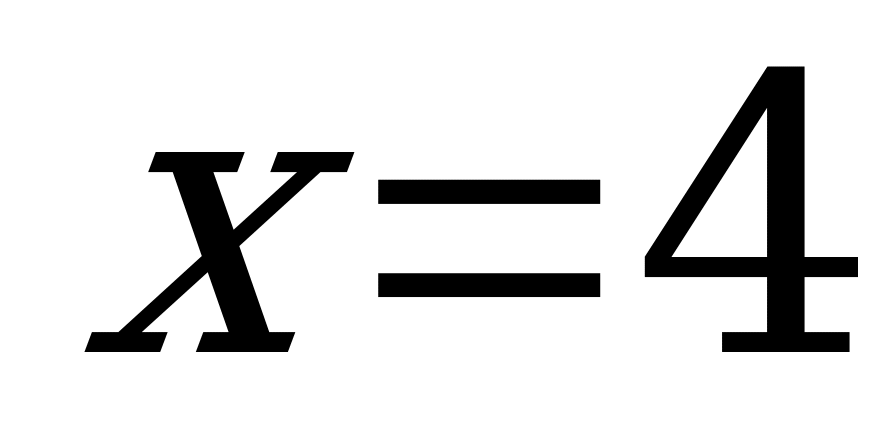 , то
, то 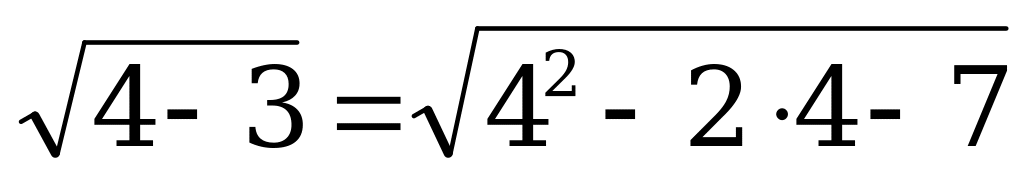 – верно.
– верно.
Если 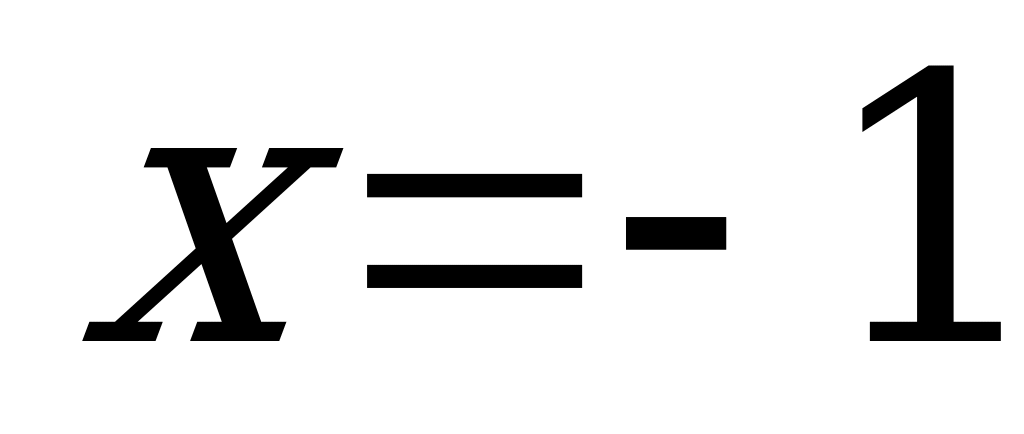 , то
, то 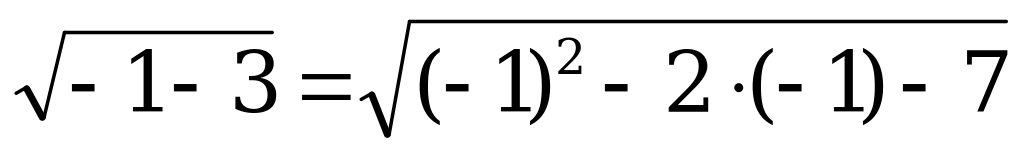 – неверно.
– неверно.
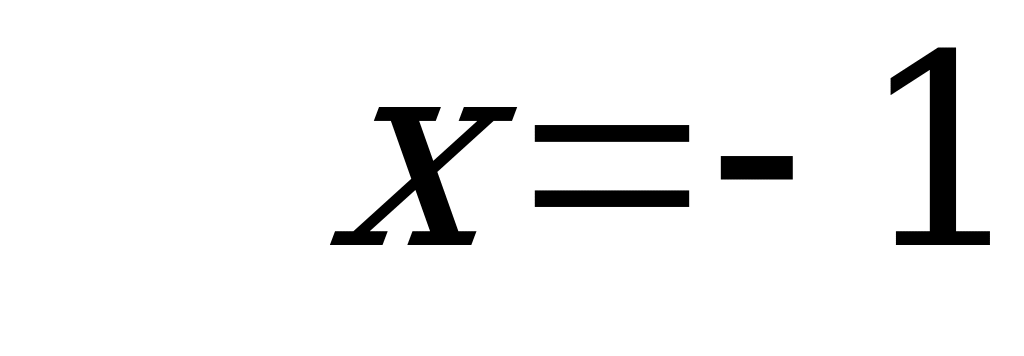 – посторонний корень.
– посторонний корень.
Ответ: 4.
В2. Найдите значение выражения 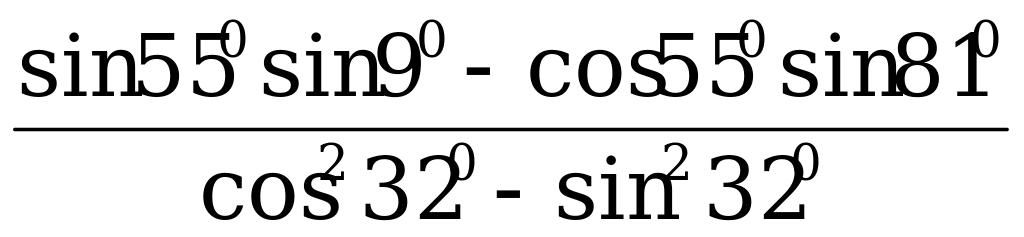 .
.
Решение:
Используем формулы 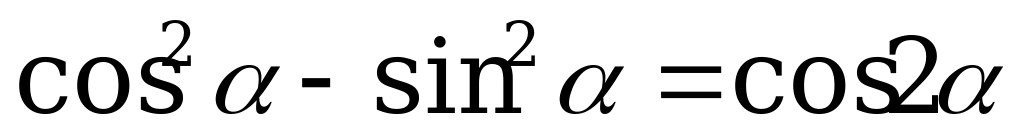 ,
, 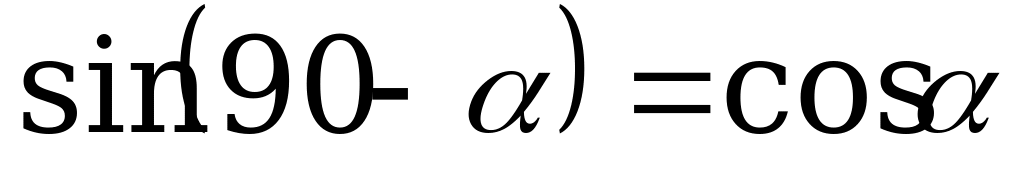 , получим
, получим
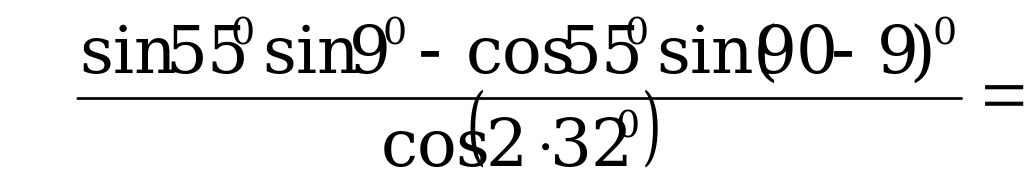
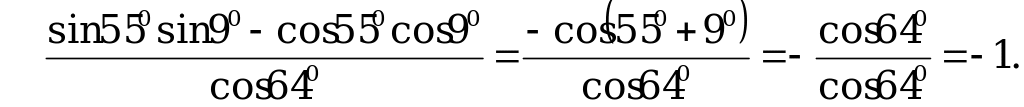
Ответ: – 1.
В3. Найдите точку максимума функции 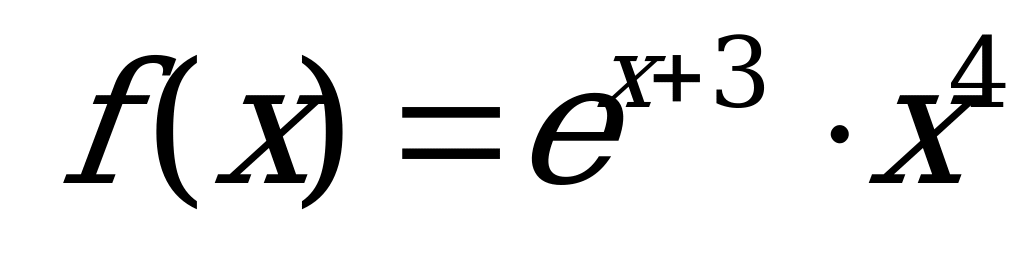 .
.
Решение:
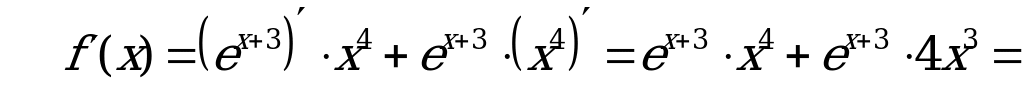
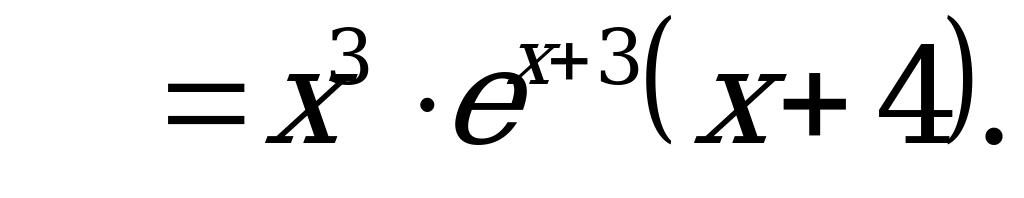
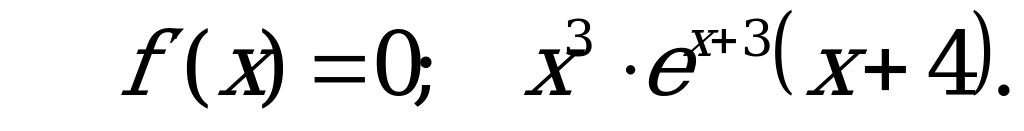
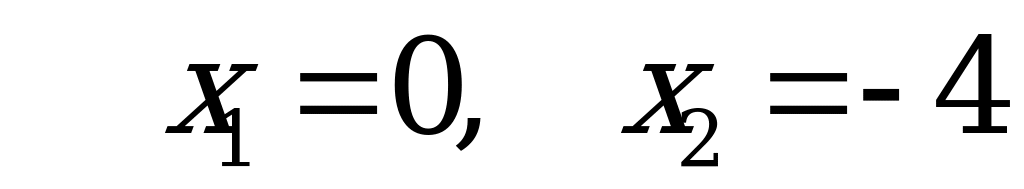 – критические точки.
– критические точки.
Определим знаки производной.

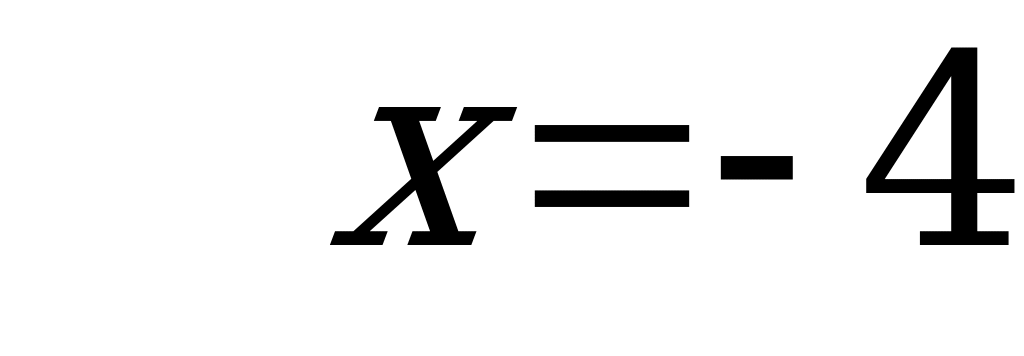 – точка максимума.
– точка максимума.
Ответ: – 4.
В4. Решите уравнение 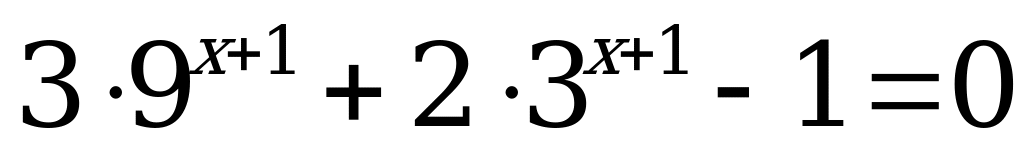 .
.
Решение:
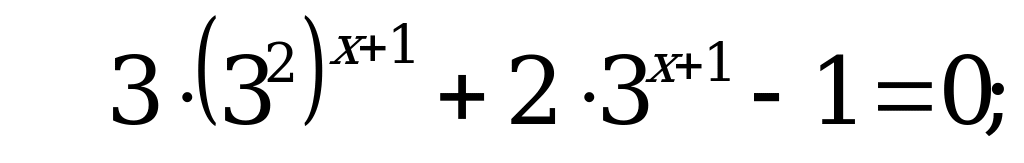
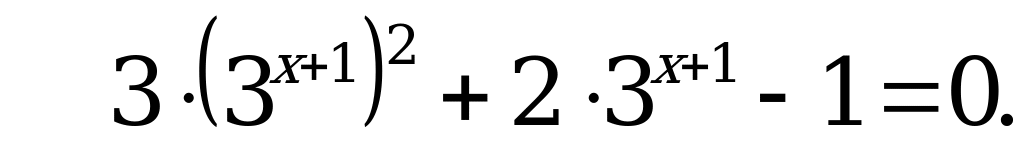
Обозначим 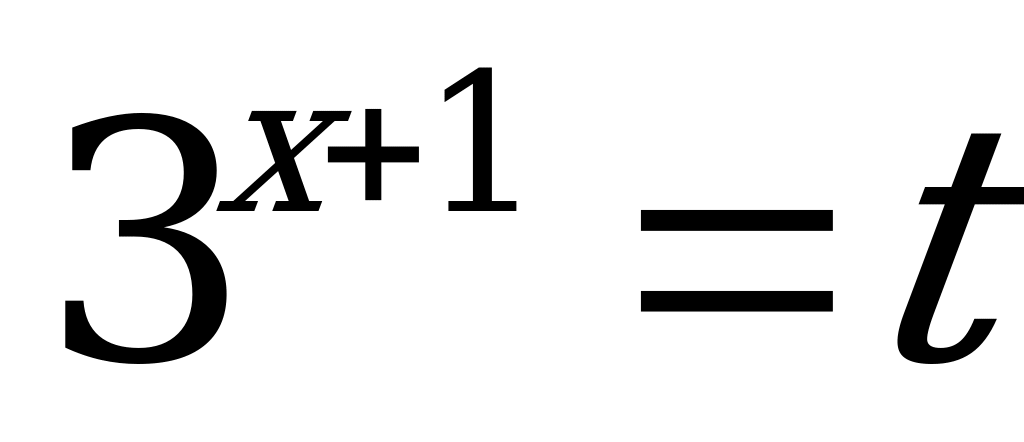 , тогда
, тогда
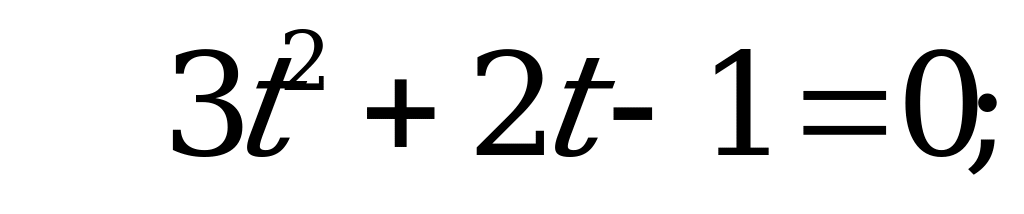
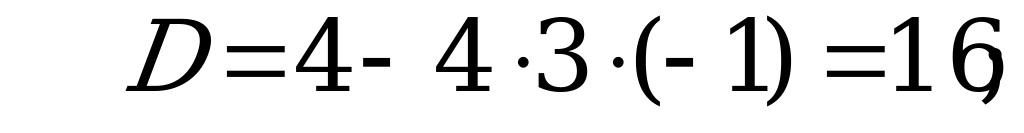
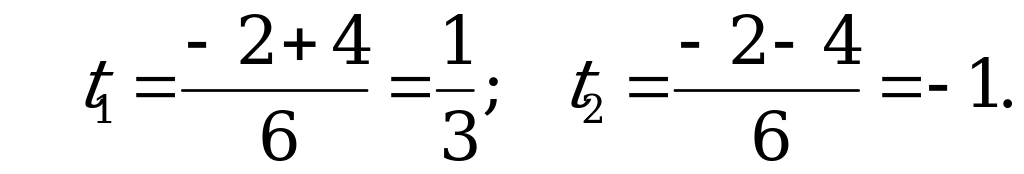
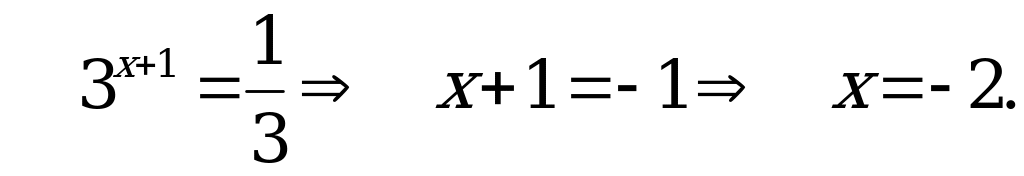 .
.
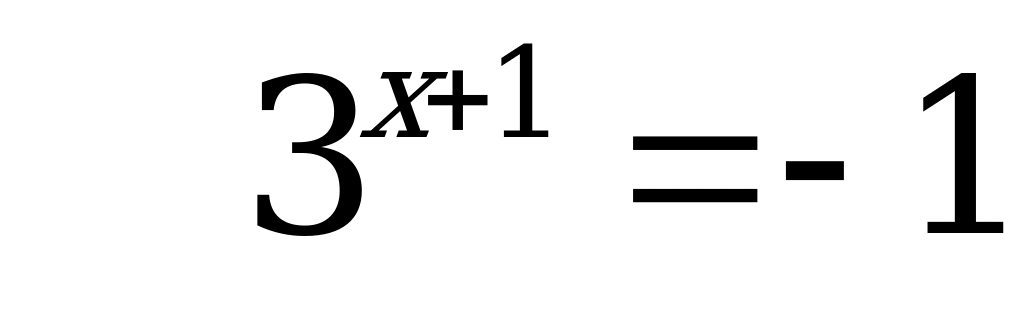 – нет решений.
– нет решений.
Ответ: – 2.
В5. Катер прошел по течению реки расстояние от пункта А до пункта В за 3 часа, а от пункта В до А за 5 часов. За сколько времени проплывает от А до В плот?
Решение:
Введем обозначения: 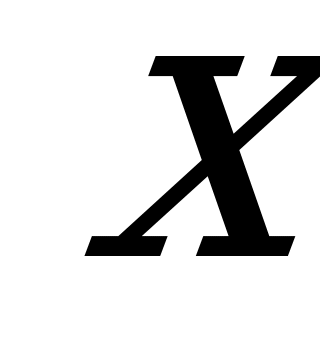 - скорость реки и плота,
- скорость реки и плота, 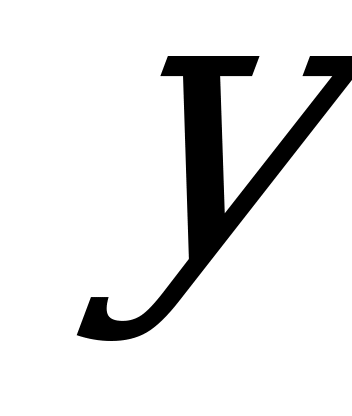 - скорость катера,
- скорость катера, 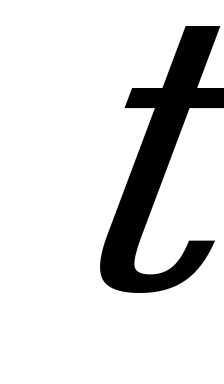 - время, за которое плот проплывает от А до В,
- время, за которое плот проплывает от А до В, 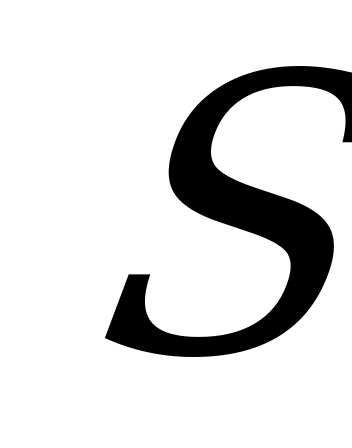 - расстояние от А до В.
- расстояние от А до В.
Получим следующие уравнения: 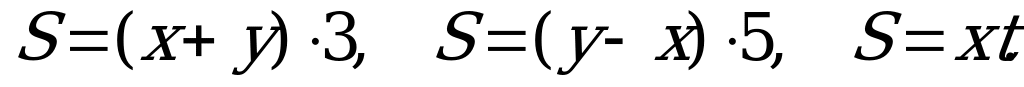
Составим и решим систему относительно переменной 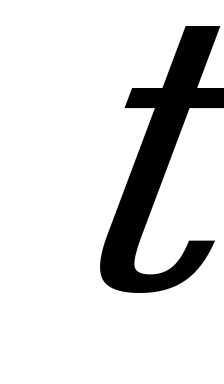 :
:
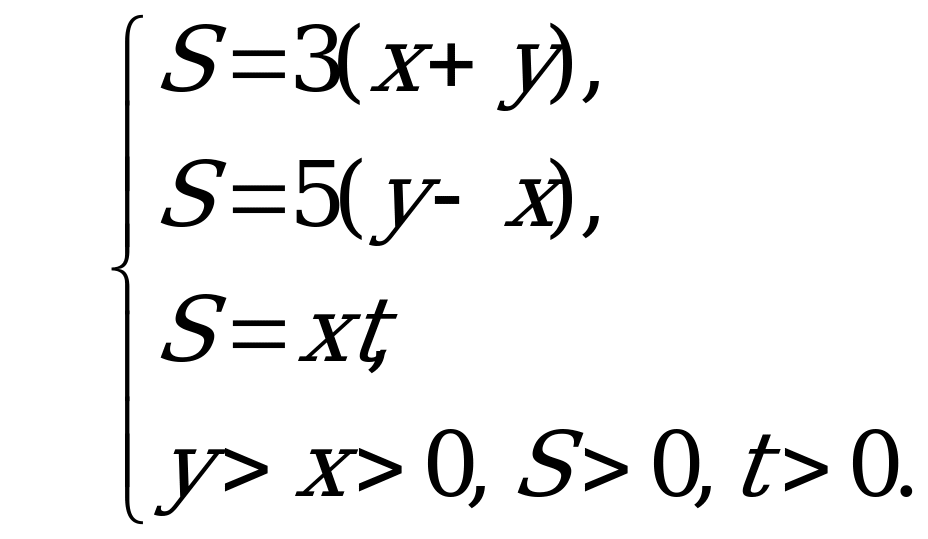

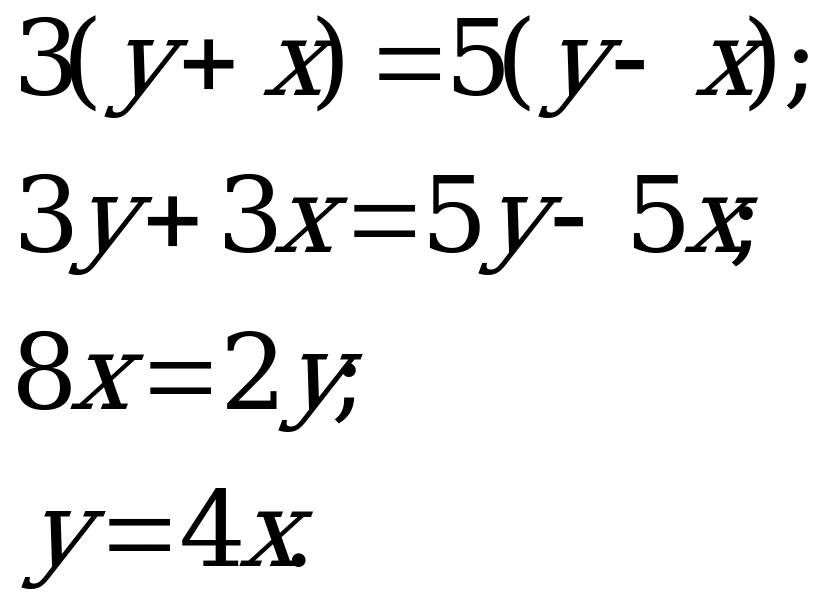

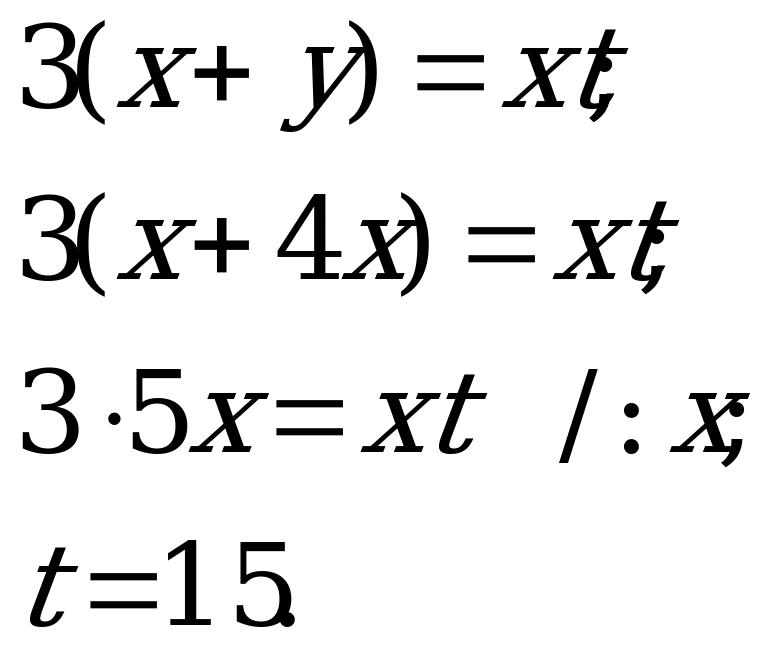
Время, которое плыл плот 15 часов.
Ответ: 15.
В6. Найдите число целых решений неравенства 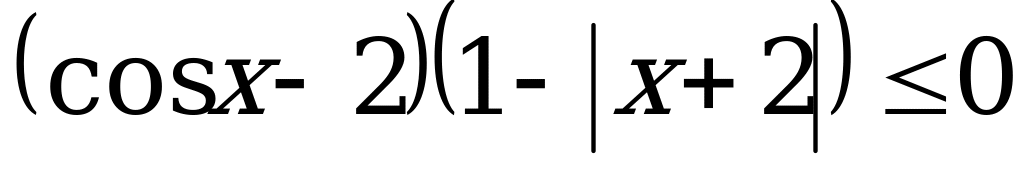 .
.
Решение:
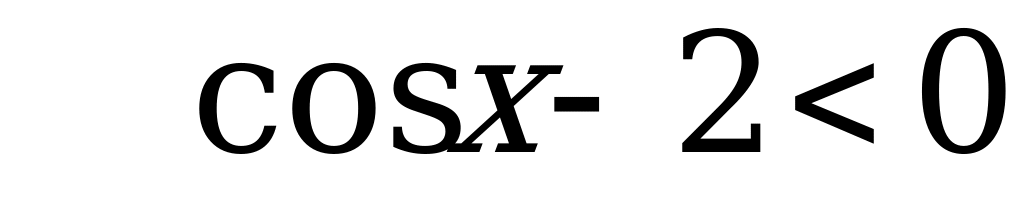 при любых значениях
при любых значениях  , значит
, значит
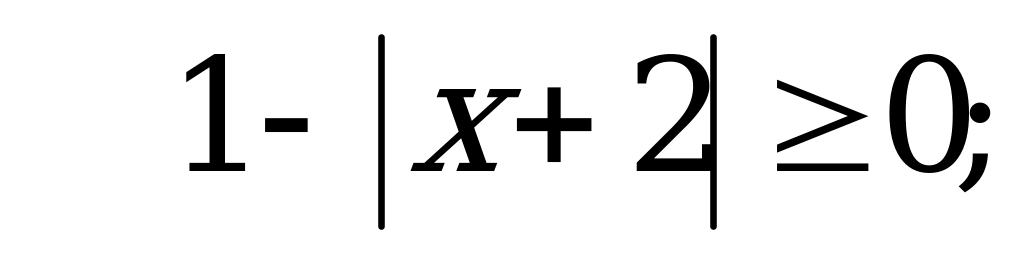
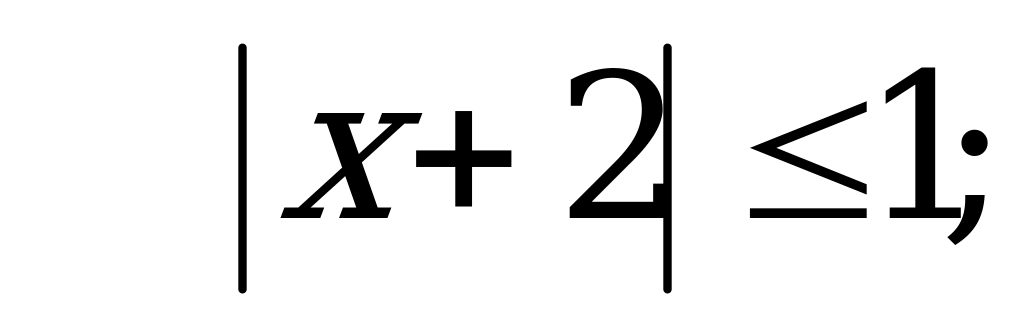
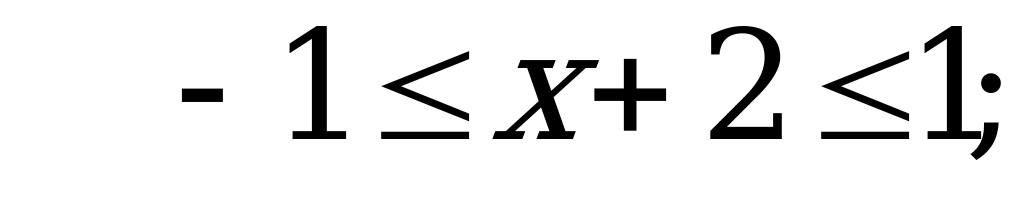
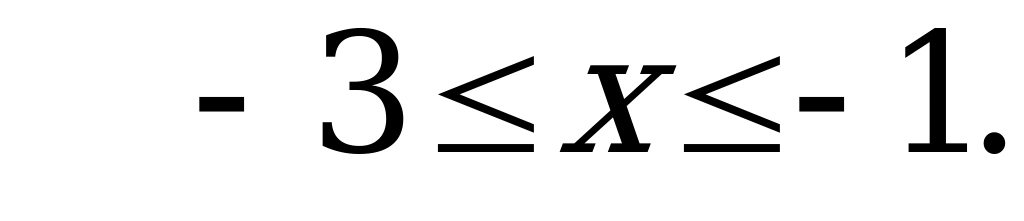
Целые числа, входящие в отрезок 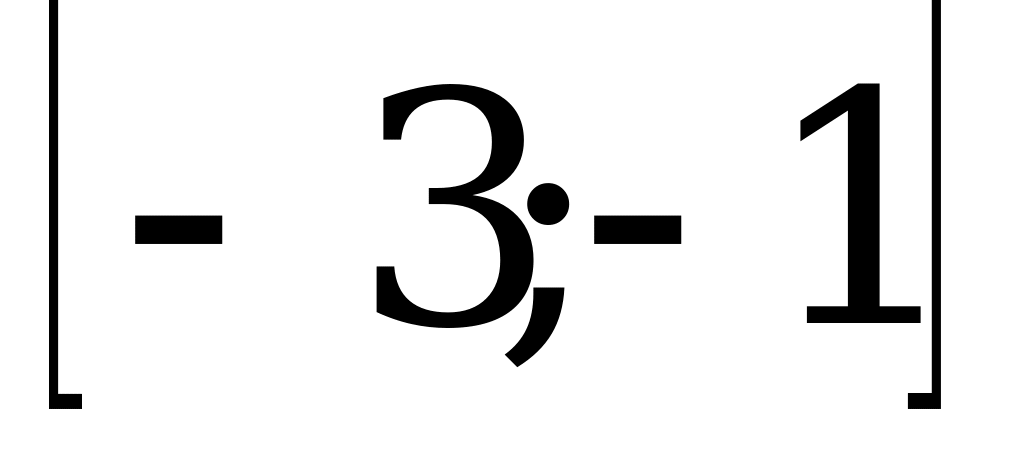 :
: 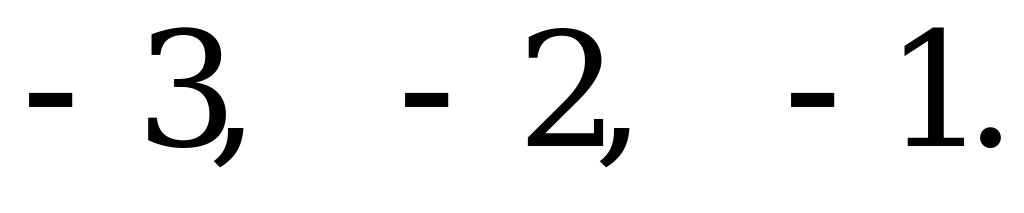 Получилось три целых решения.
Получилось три целых решения.
Ответ: 3.
В7. Найдите наибольшее целое значение параметра 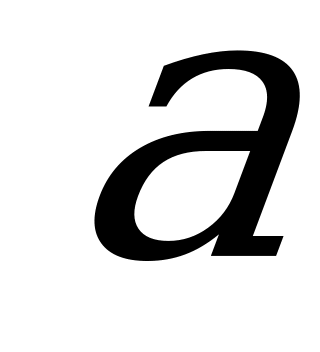 , при котором решение системы уравнений
, при котором решение системы уравнений 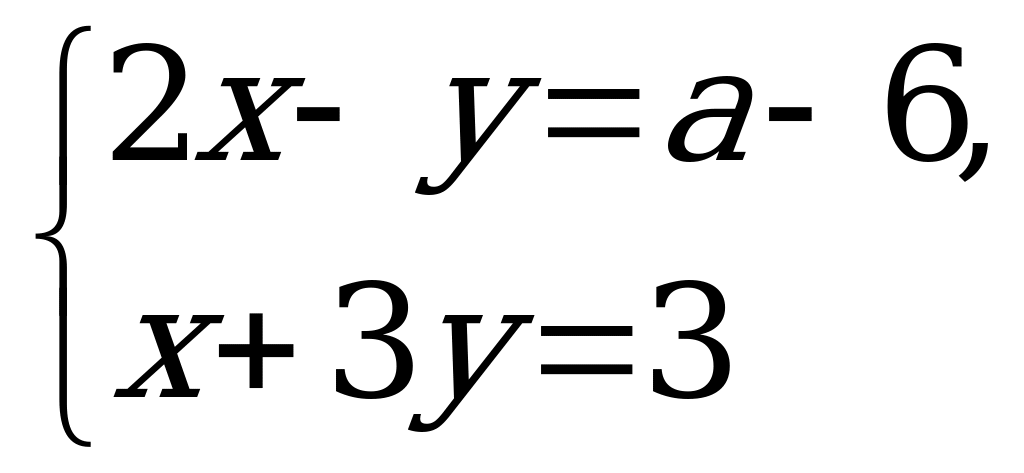 удовлетворяет неравенству
удовлетворяет неравенству 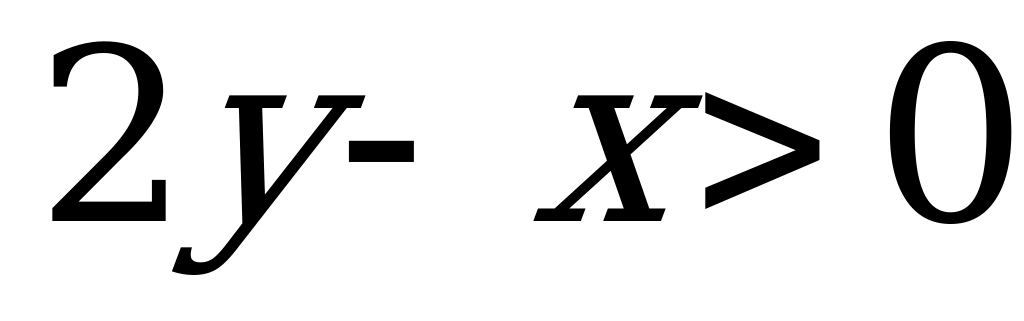 .
.
Решение:
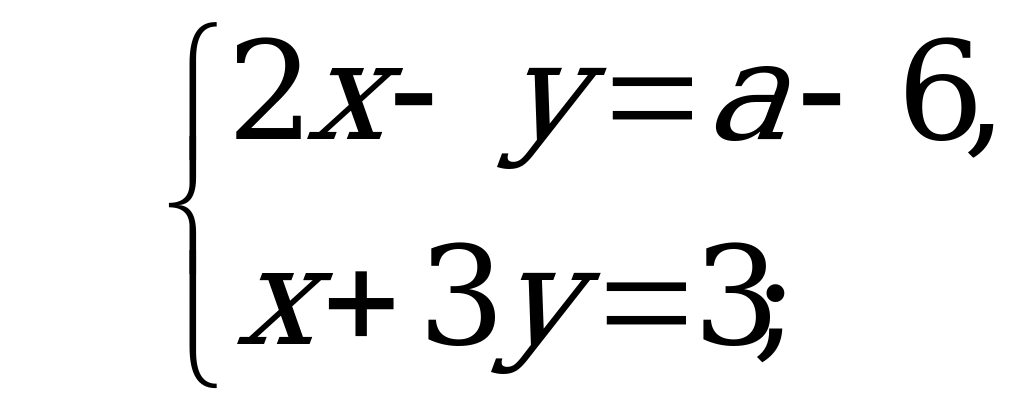

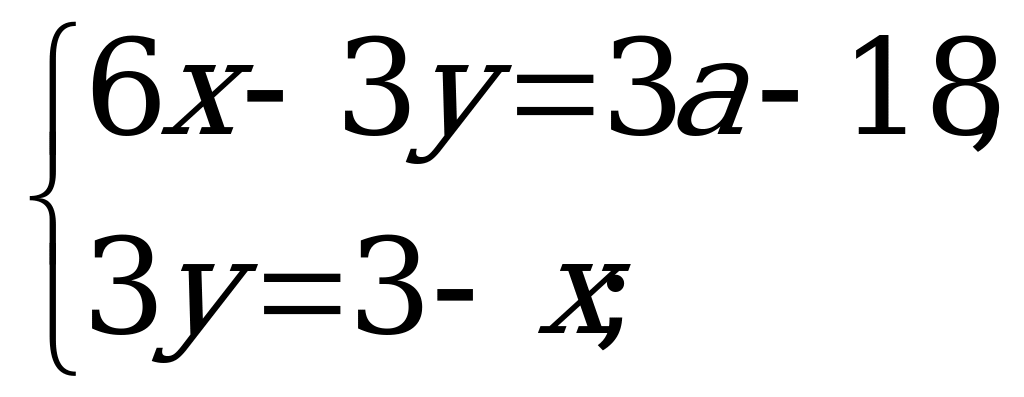

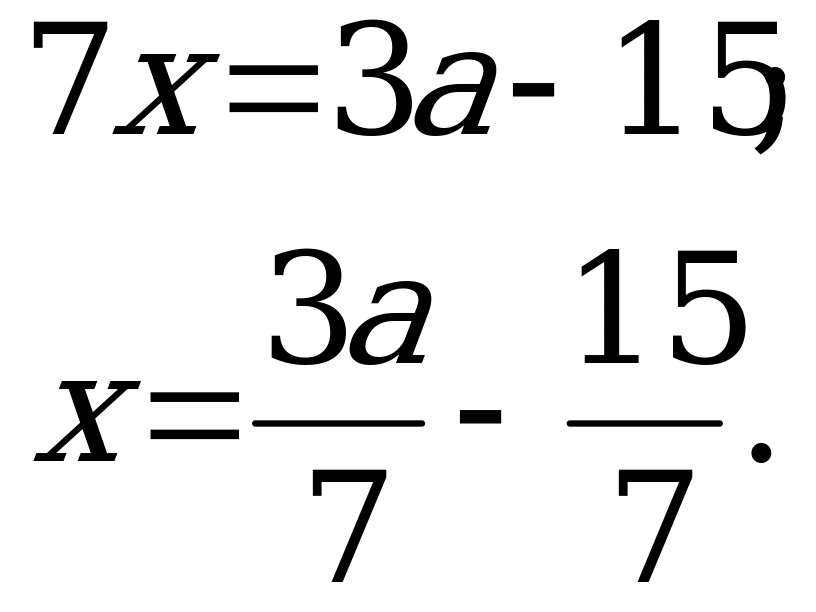
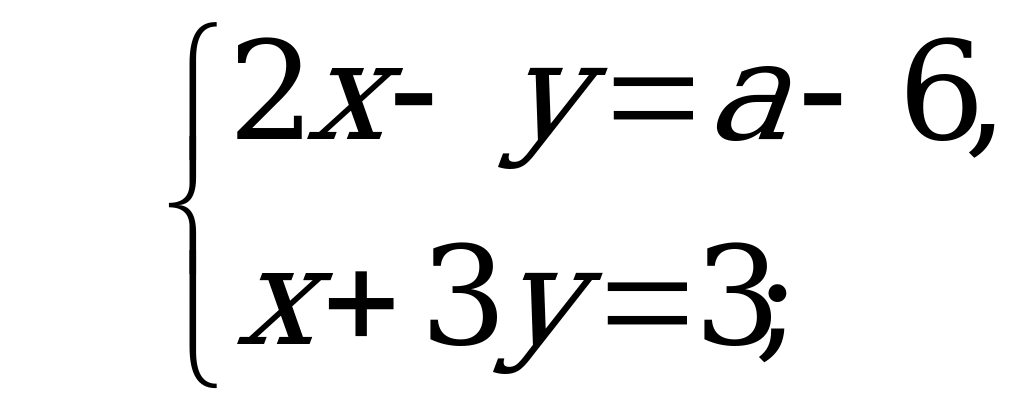

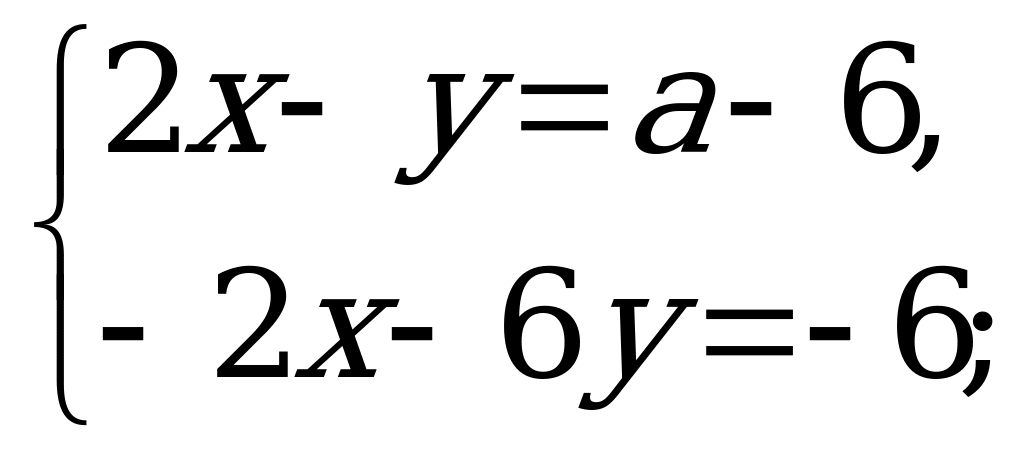

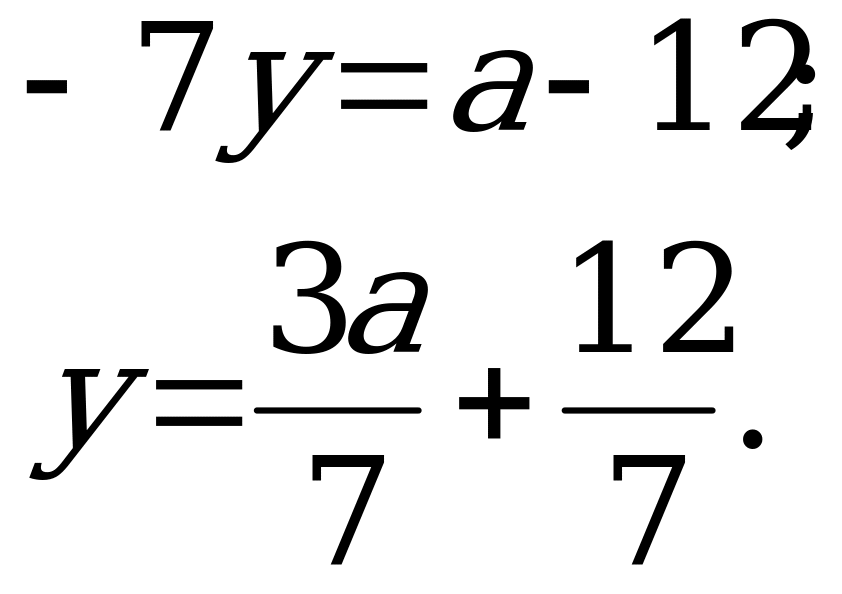
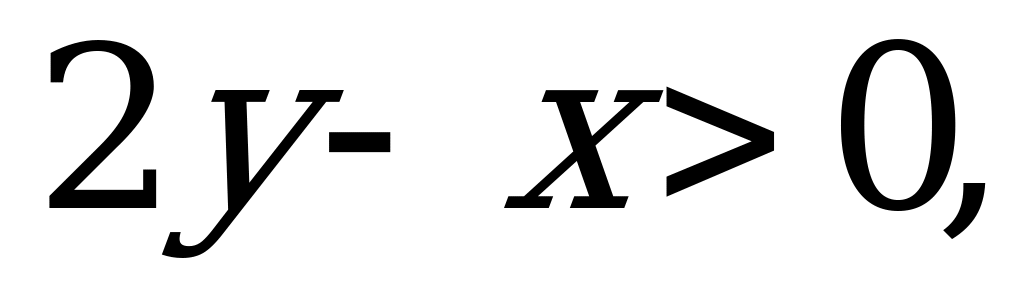 значит
значит 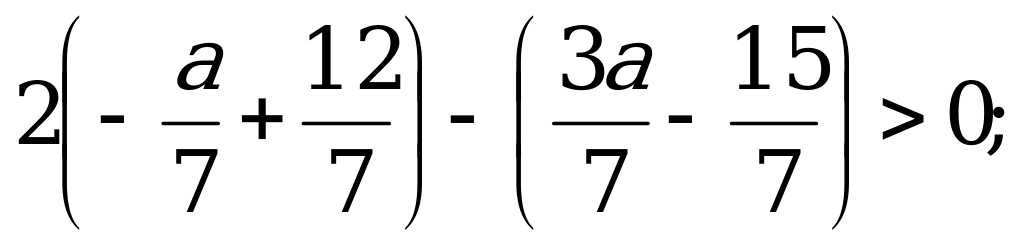
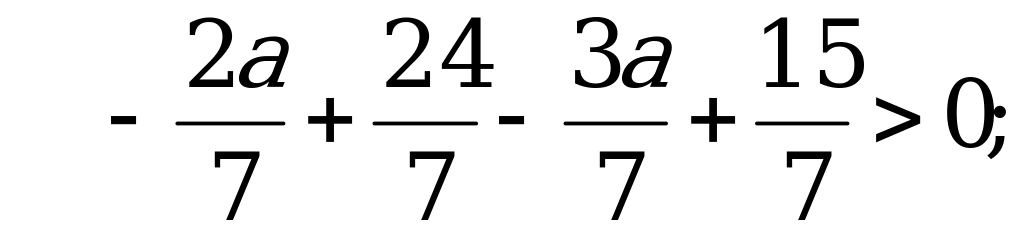
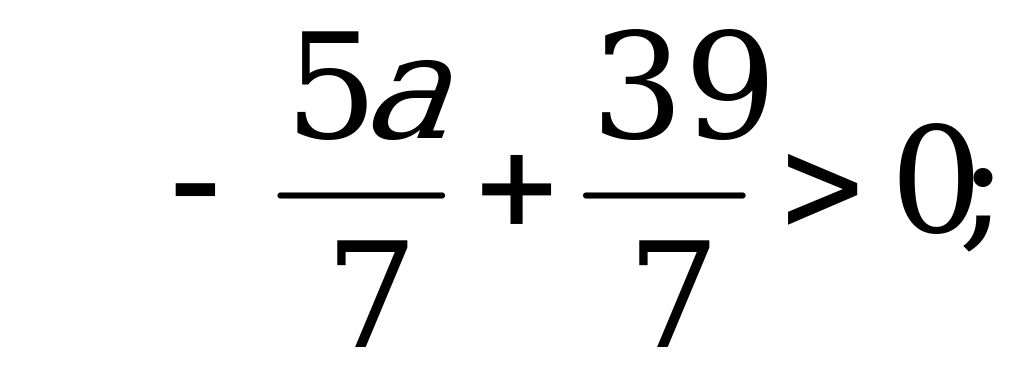
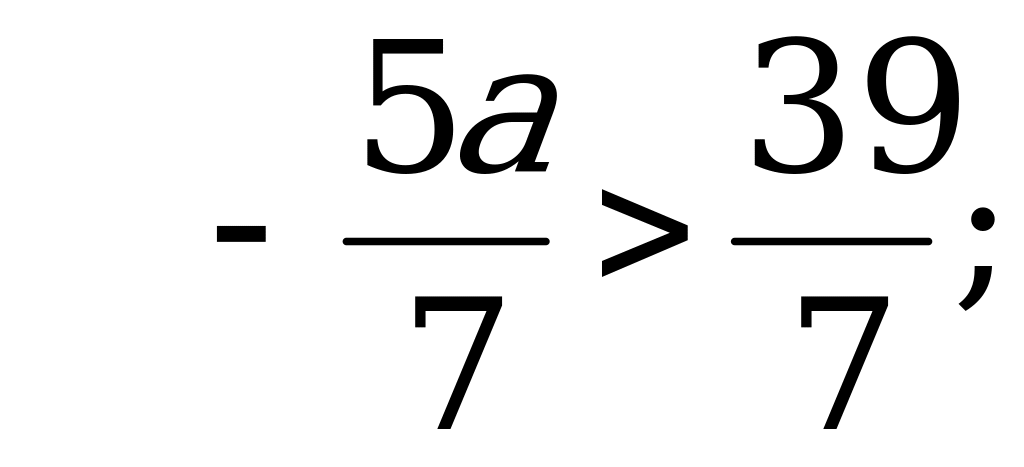
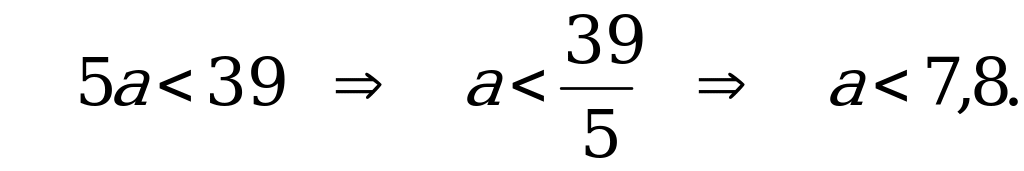
Следовательно, 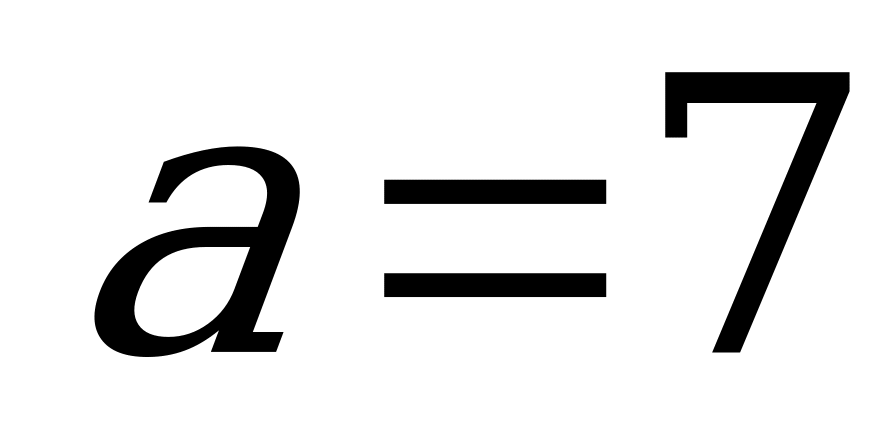 – наибольшее целое значение параметра
– наибольшее целое значение параметра  .
.
Ответ: 7.
В8. Высота правильной четырехугольной пирамиды равна 3, апофема образует с плоскостью основания угол  . Найдите площадь боковой поверхности пирамиды.
. Найдите площадь боковой поверхности пирамиды.
Решение:
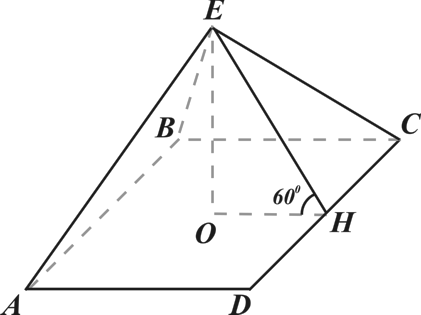
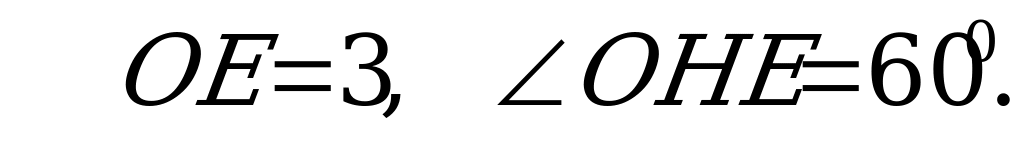
Из 
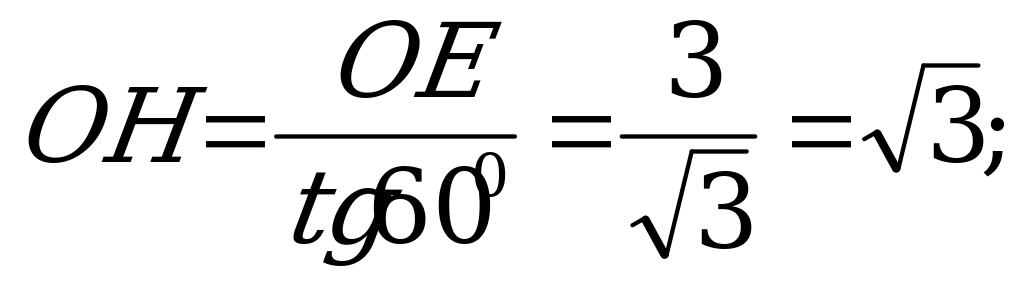
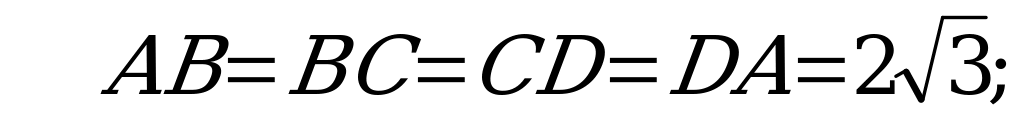
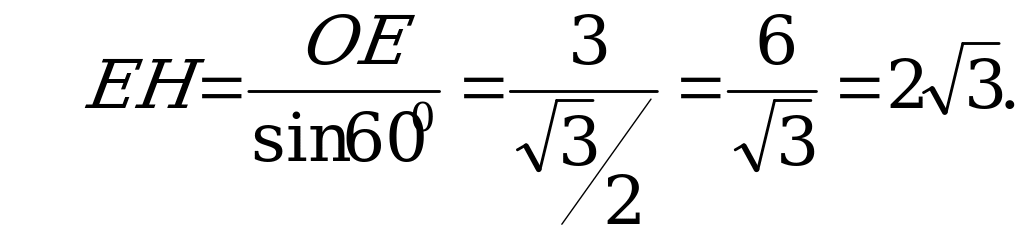
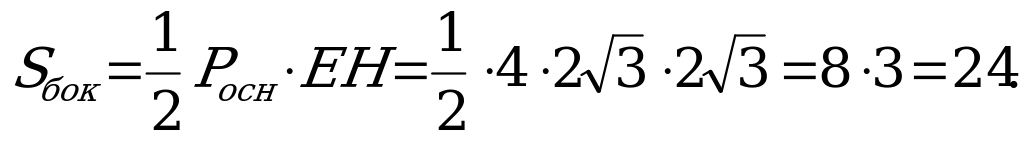
Ответ: 24.
В9. Площадь основания конуса равна площади поверхности вписанного в него шара. Найдите радиус шара, если образующая конуса равна 10.
Решение:
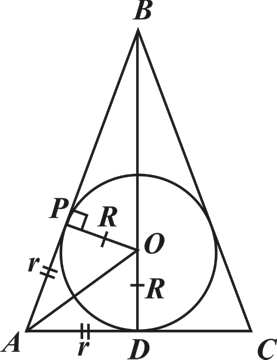
Рассмотрим осевое сечение конуса, 
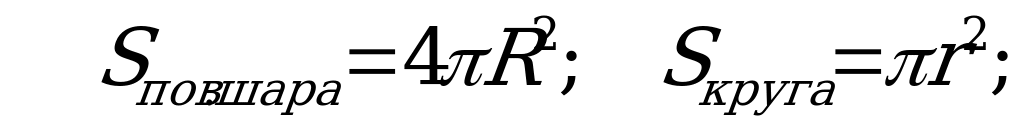
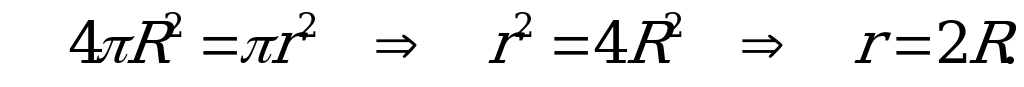
По условию 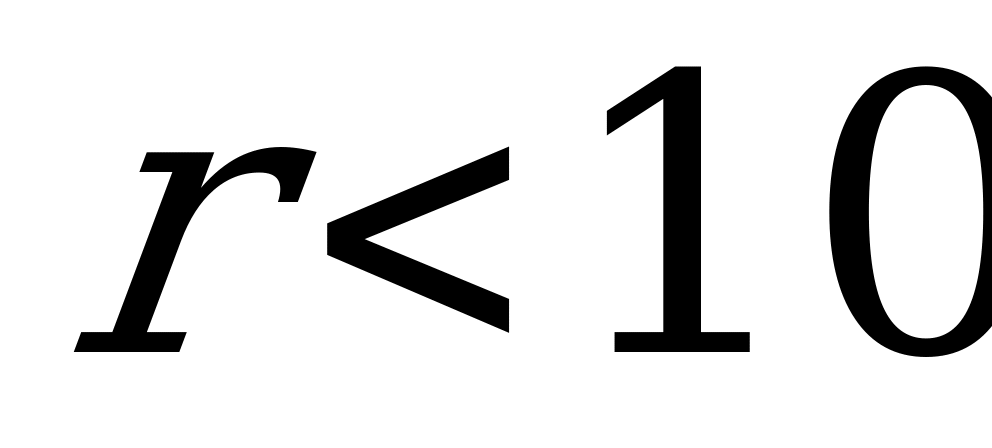 , значит
, значит 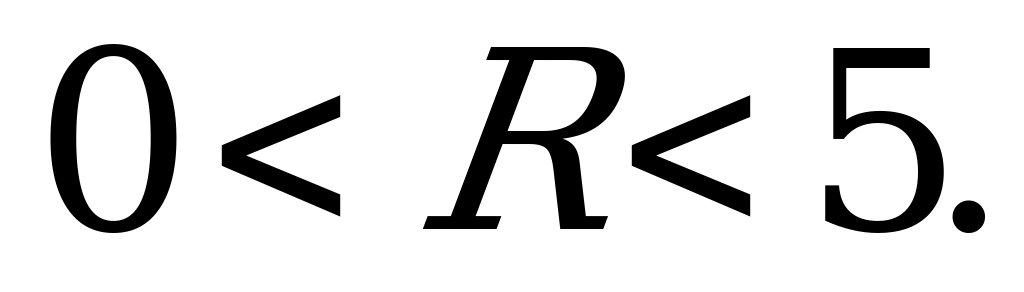
Из подобия треугольников 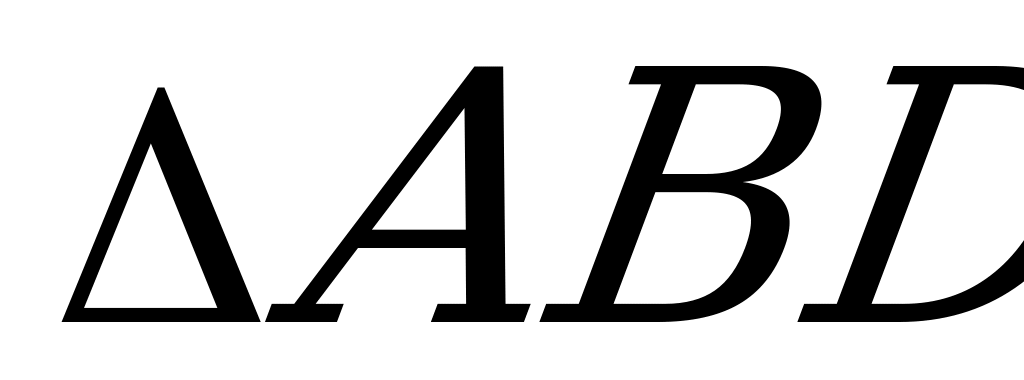 и
и 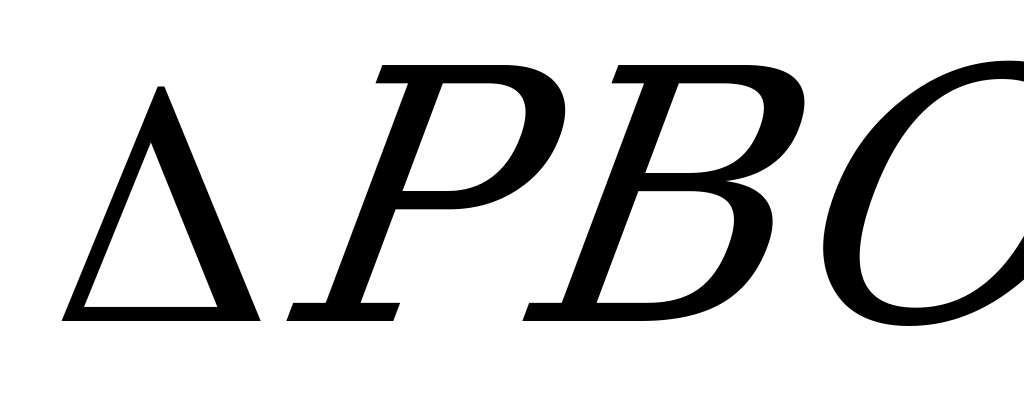 , имеем:
, имеем:
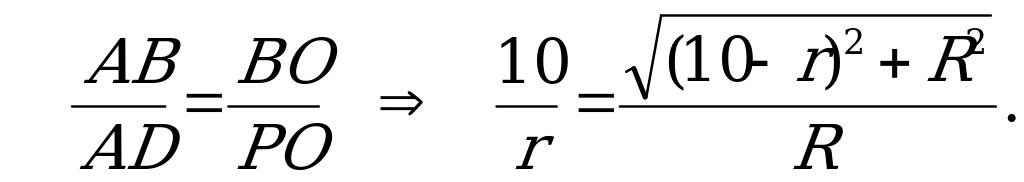
Так как 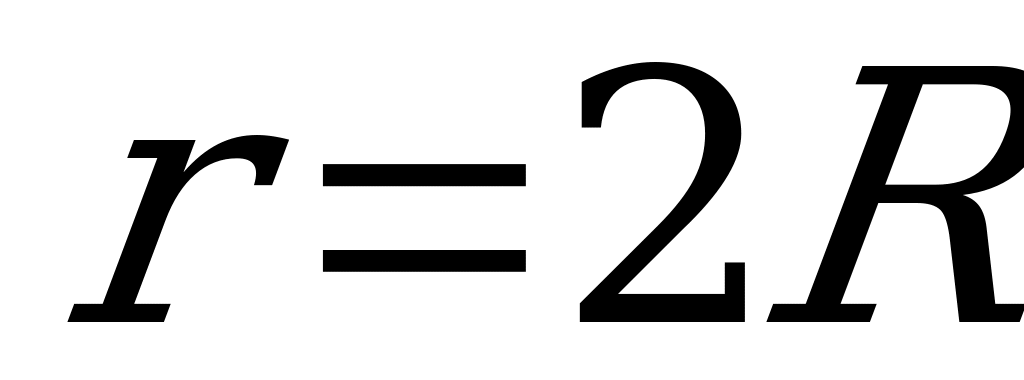 , получим
, получим 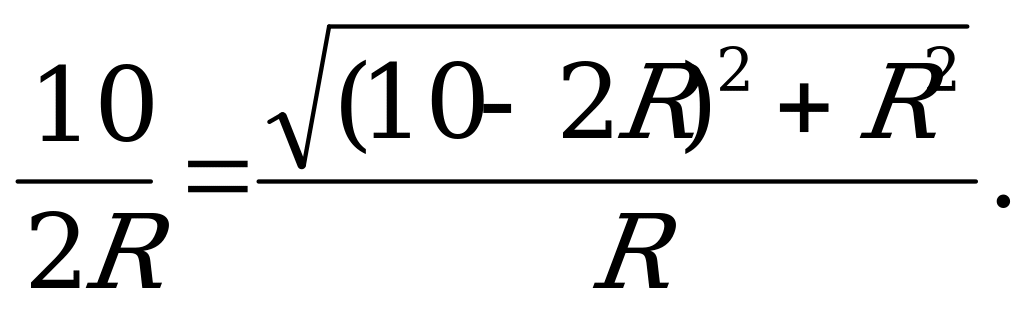
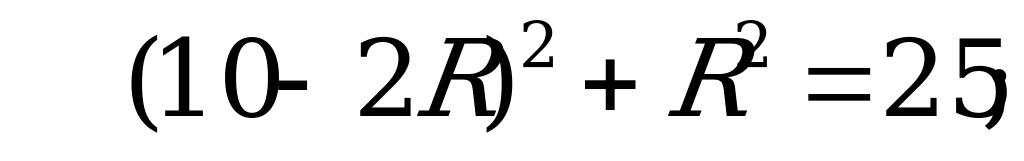
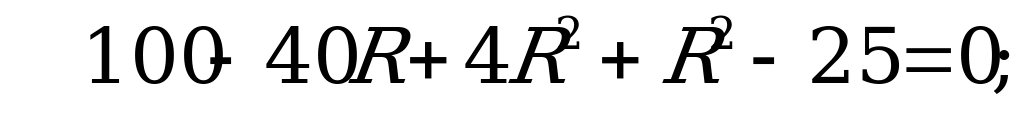
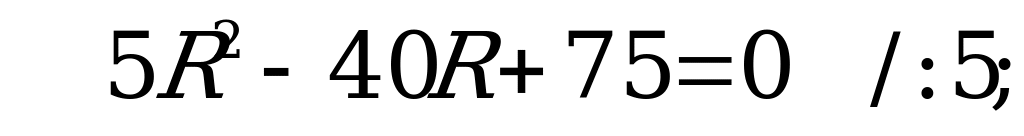
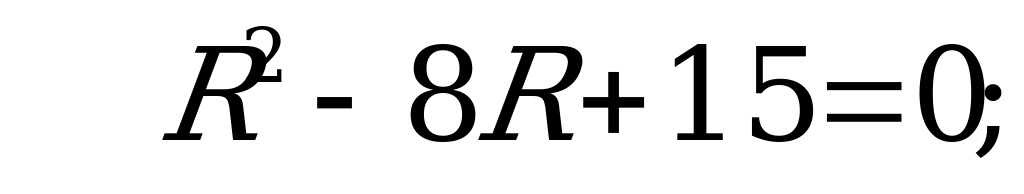
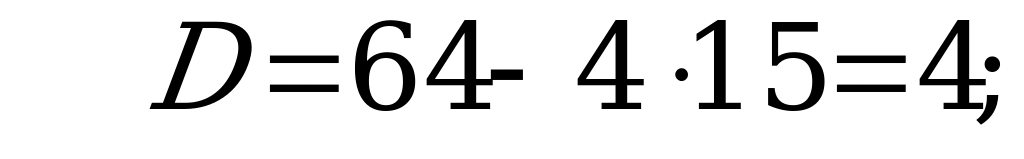
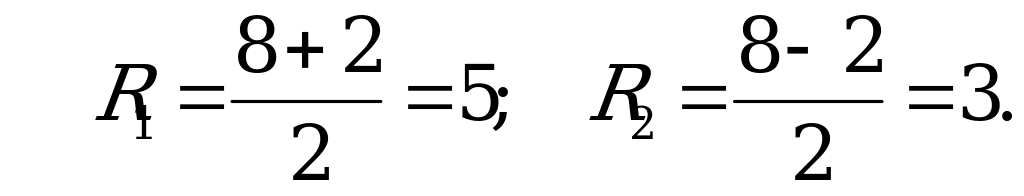
По смыслу задачи 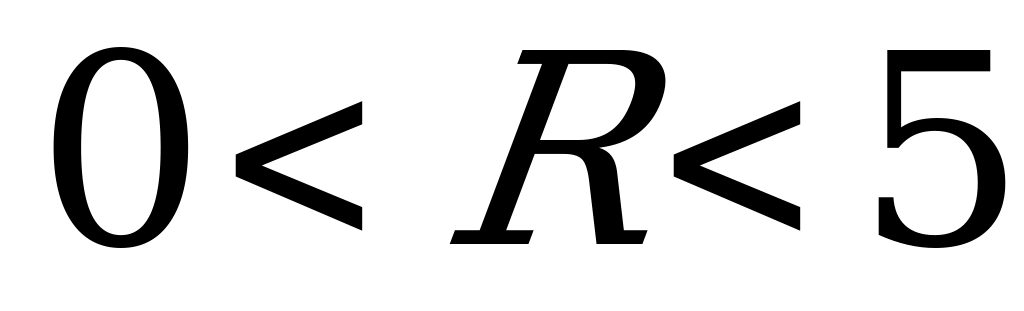 , значит
, значит 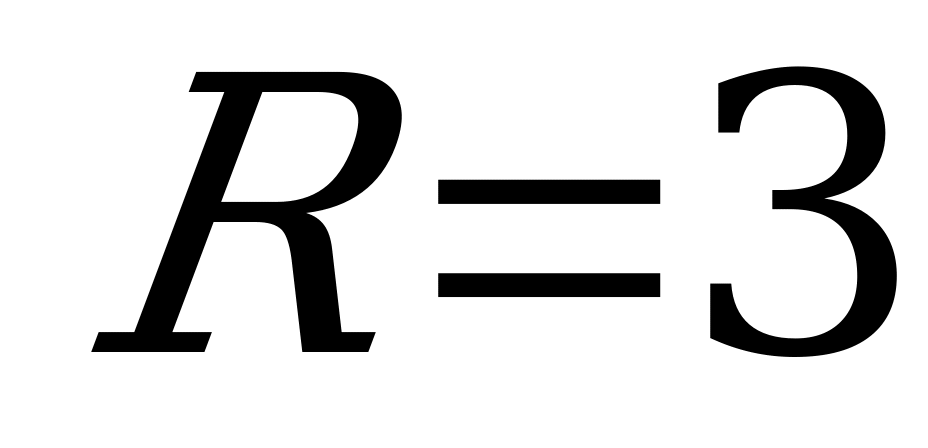 .
.
Ответ: 3.
4. Задания с развернутым ответом С1 – С3.
Часть 3.
С1: Для каждого допустимого значения параметра 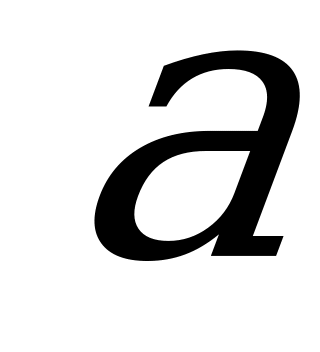 . Решите неравенство
. Решите неравенство 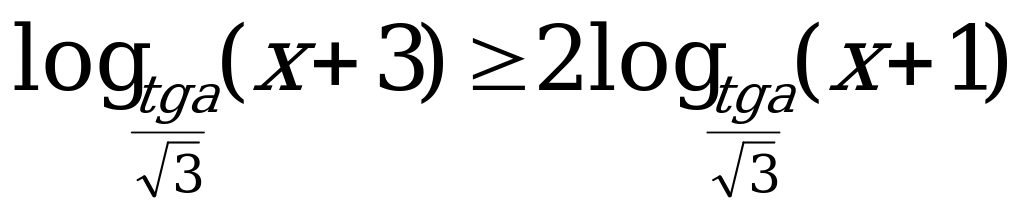 .
.
Решение:
Неравенство равносильно двум системам:
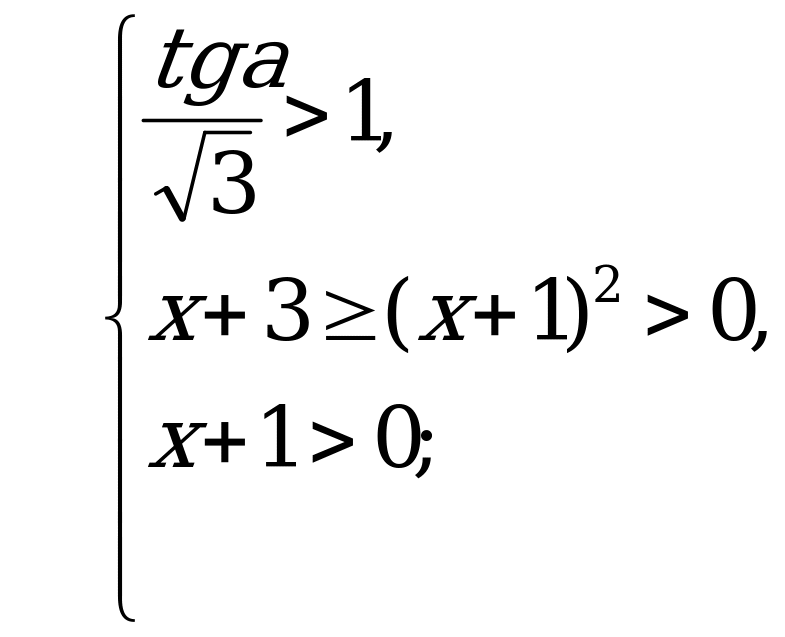 и
и 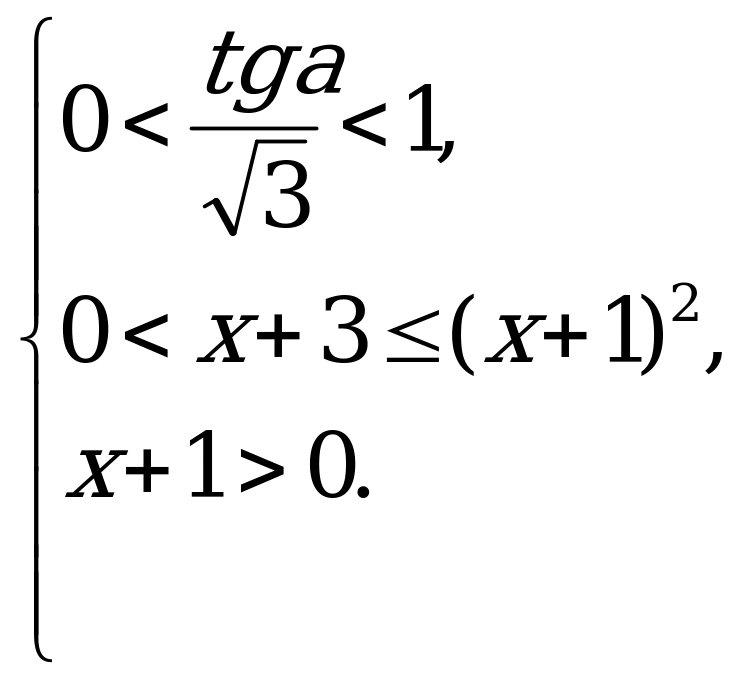
Решим «параллельно» тригонометрические неравенства.
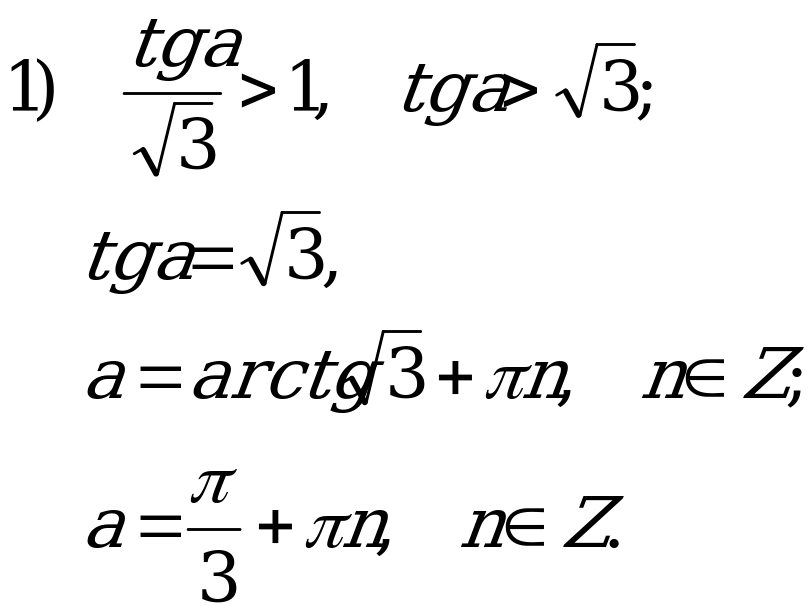
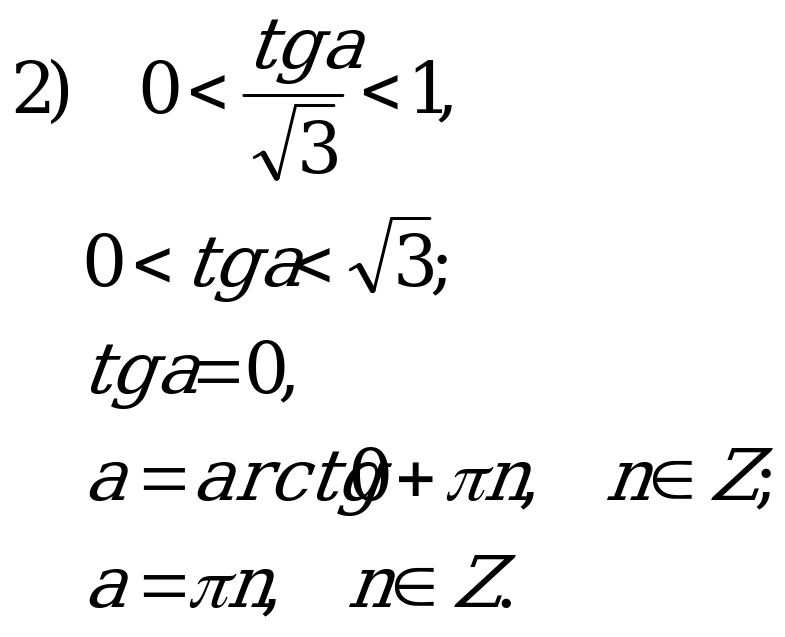
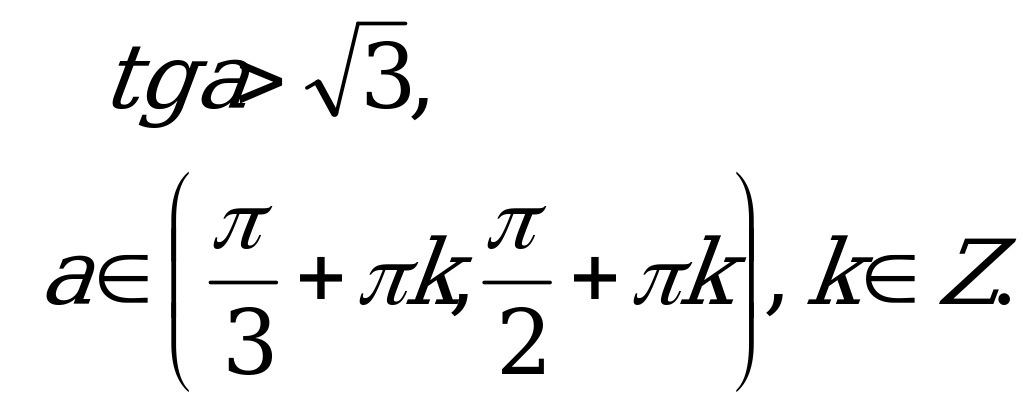
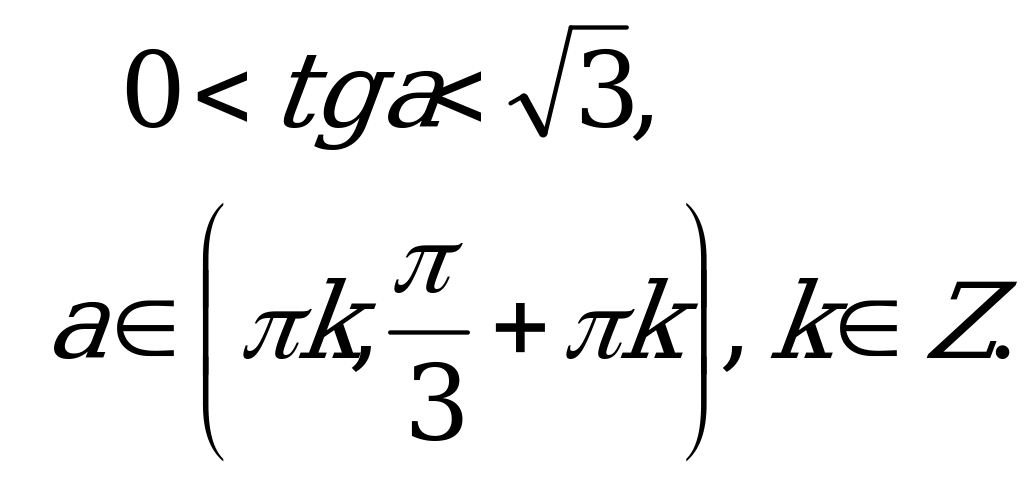
Решаем остальные неравенства систем.
1) 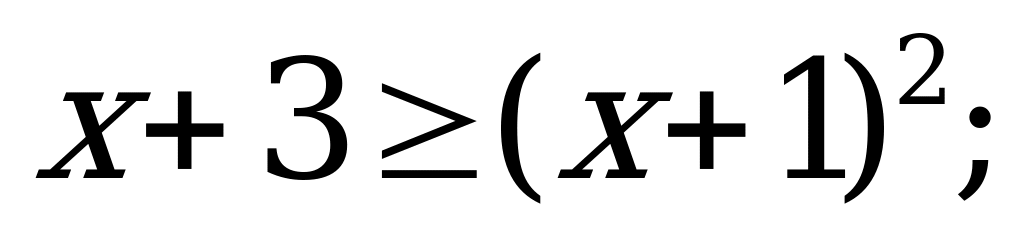
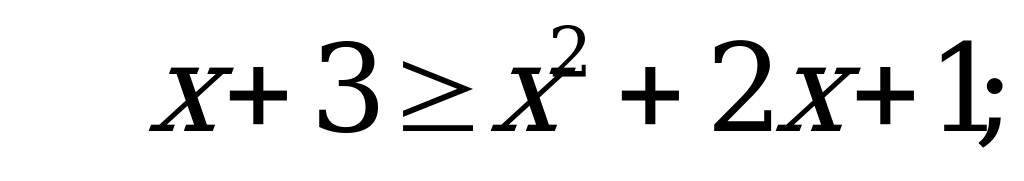
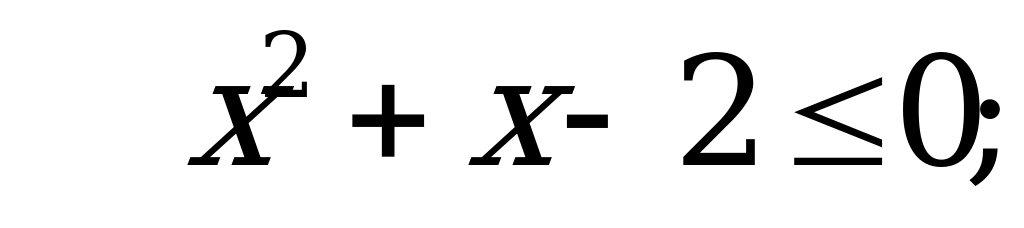
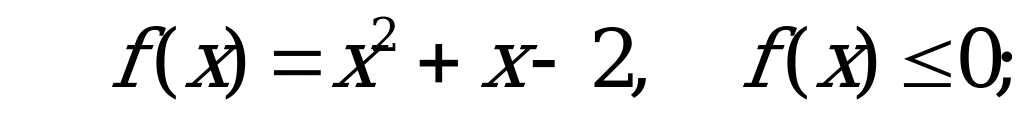
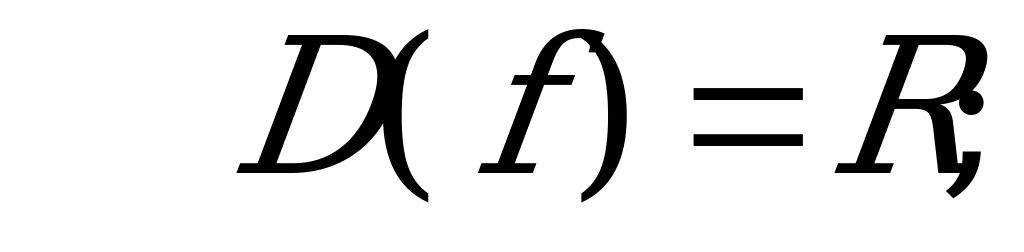
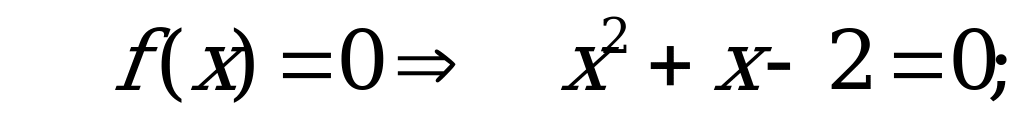
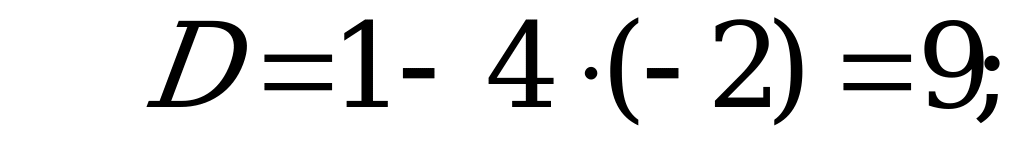
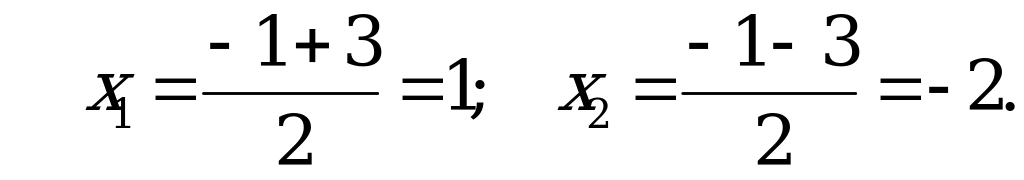
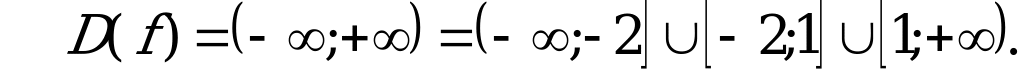
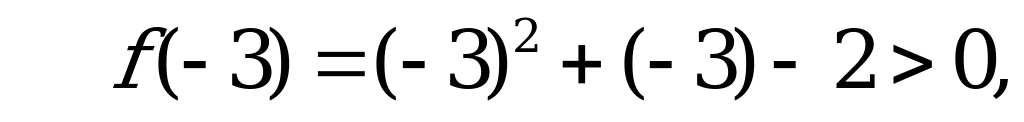
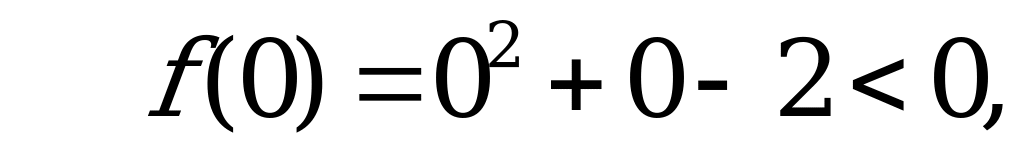
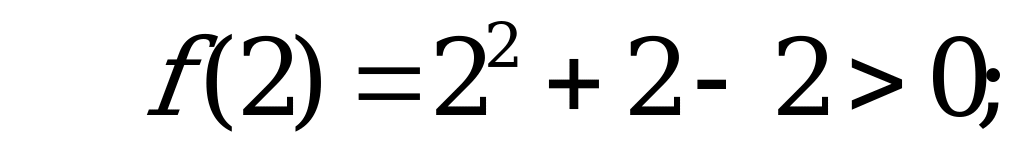
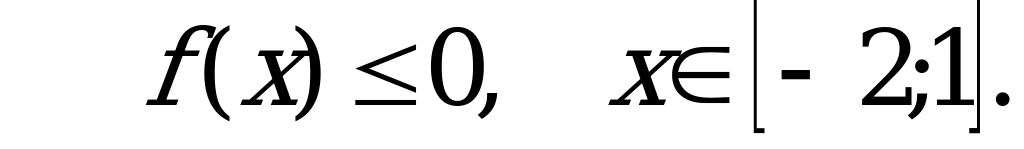
Нужно учитывать, что 

2) 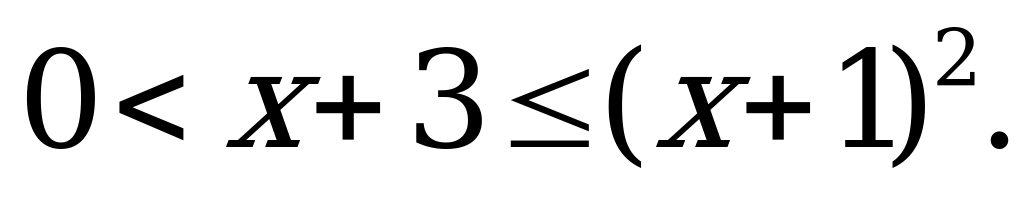
Аналогично предыдущему неравенству получаем 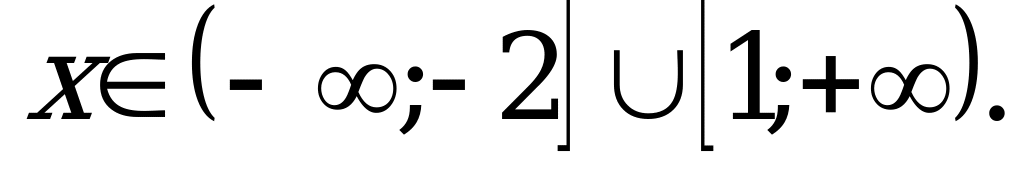
Нужно учитывать, что 

Значит, 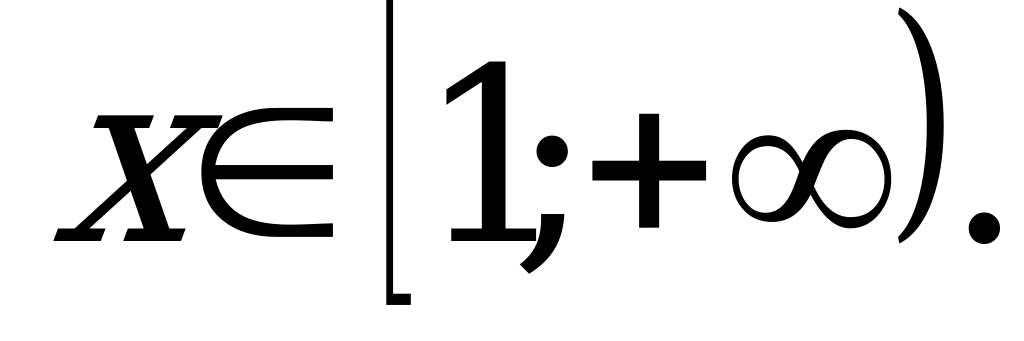
Запишем решение двух систем:
если 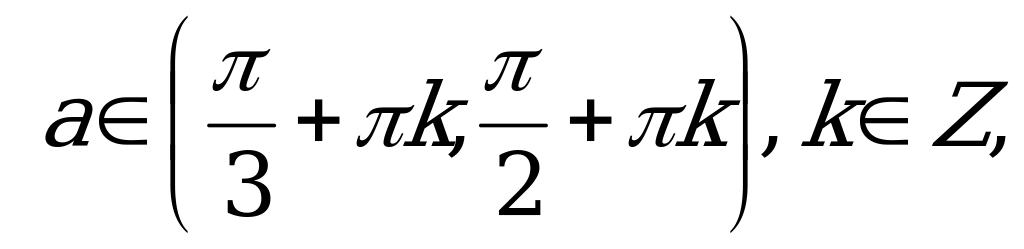 то
то 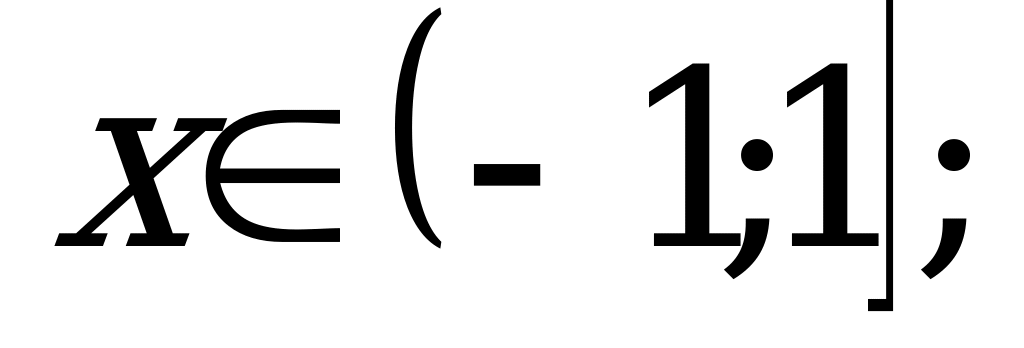
если 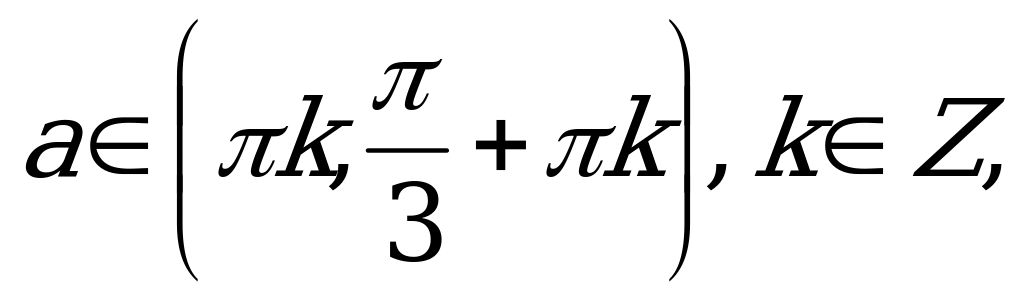 то
то 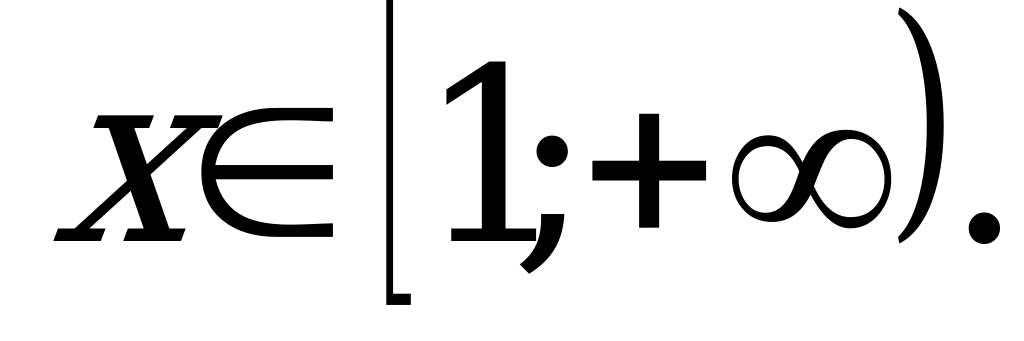
Ответ: 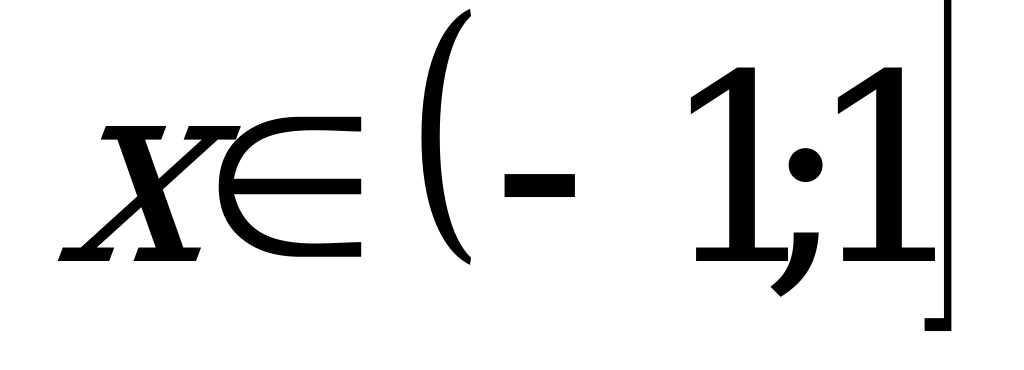 при
при 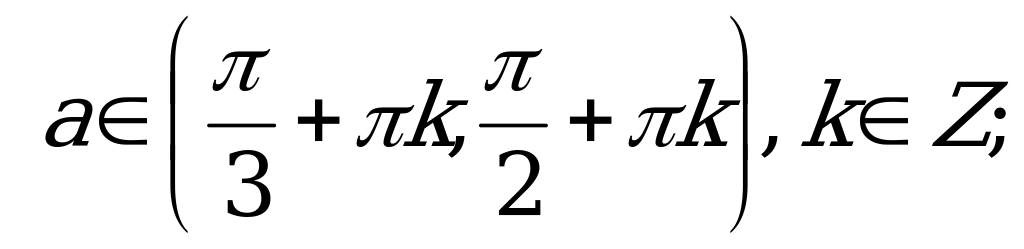
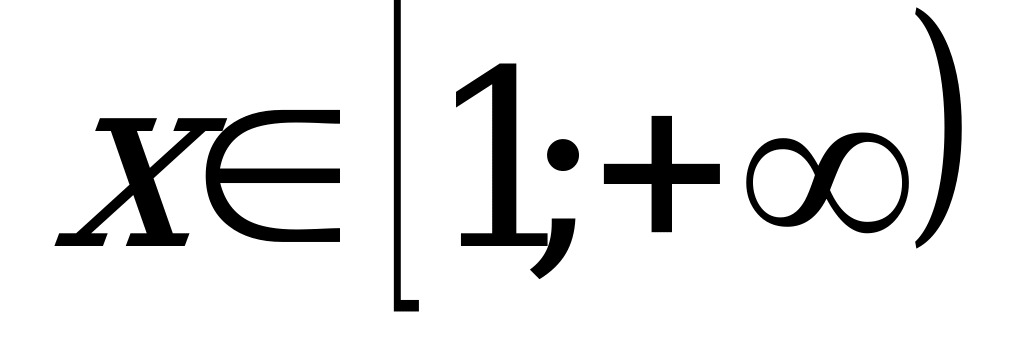 при
при 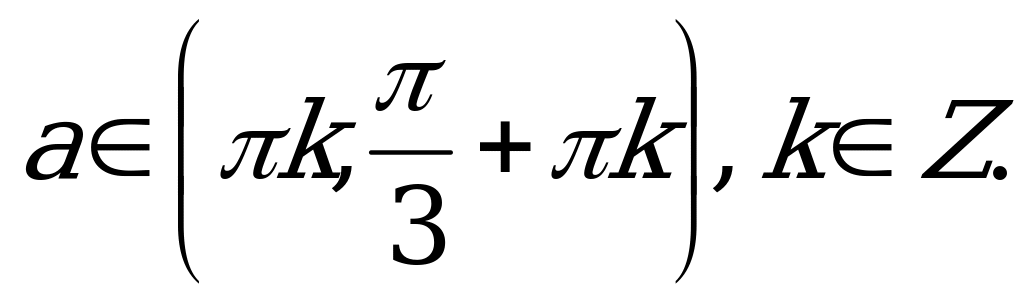
С2: Решите уравнение 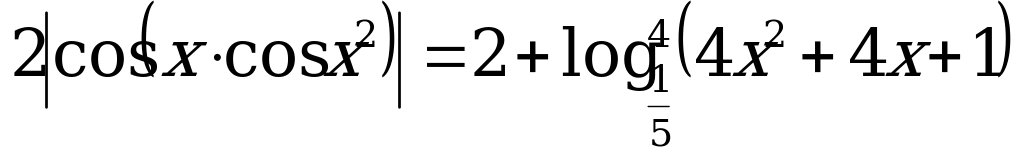 .
.
Решение:
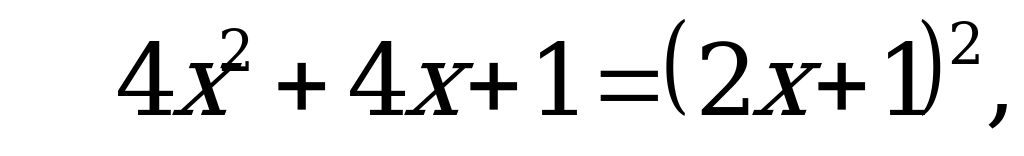
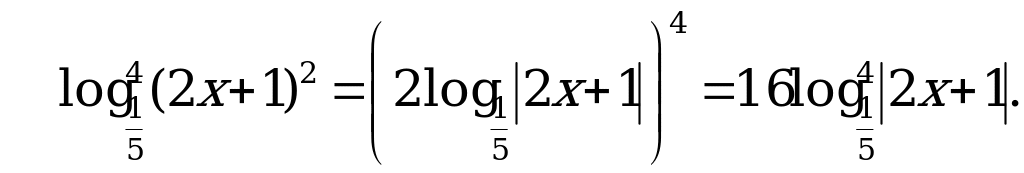
Подставим это выражение в уравнение и разделим уравнение на 2, получим 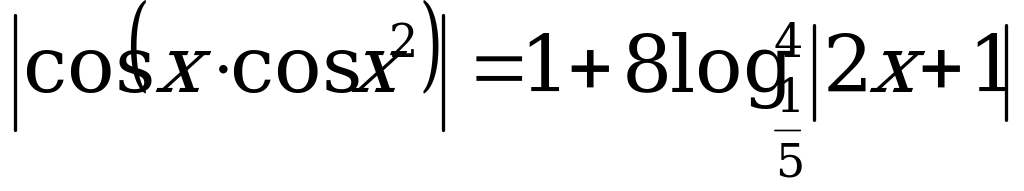 .
.
Выясним ограниченность значений функции
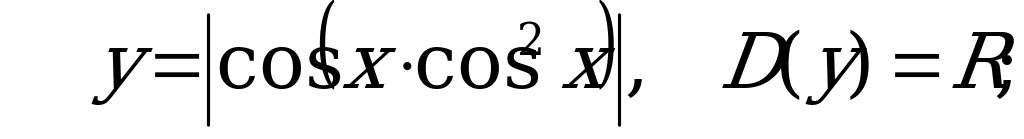
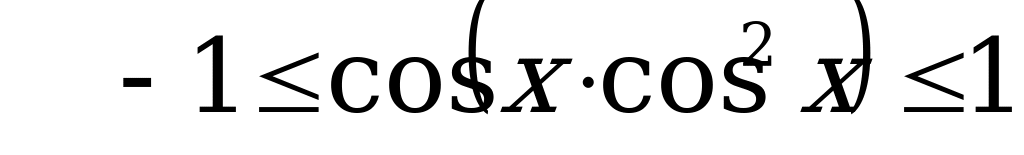 , значит
, значит 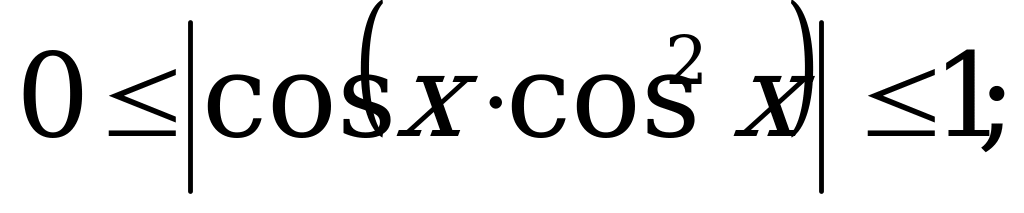
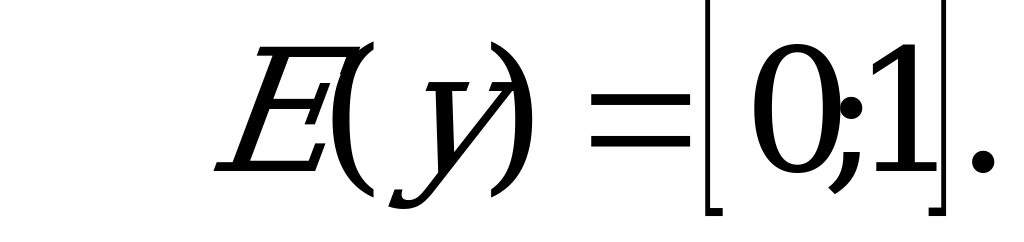
Выясним ограниченность значений функции
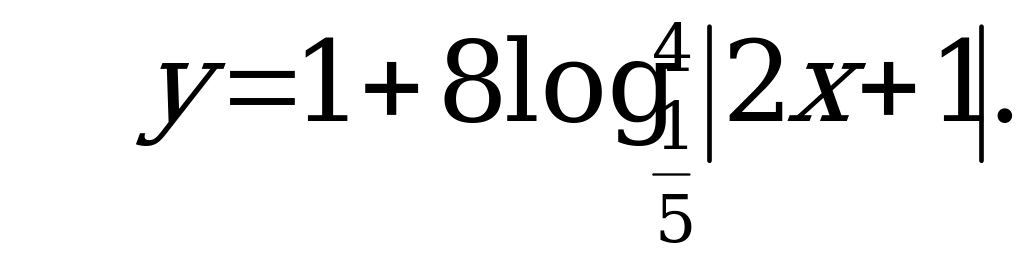
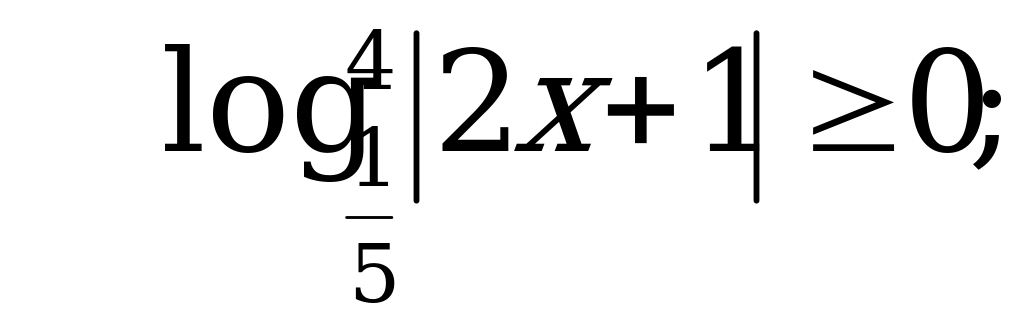
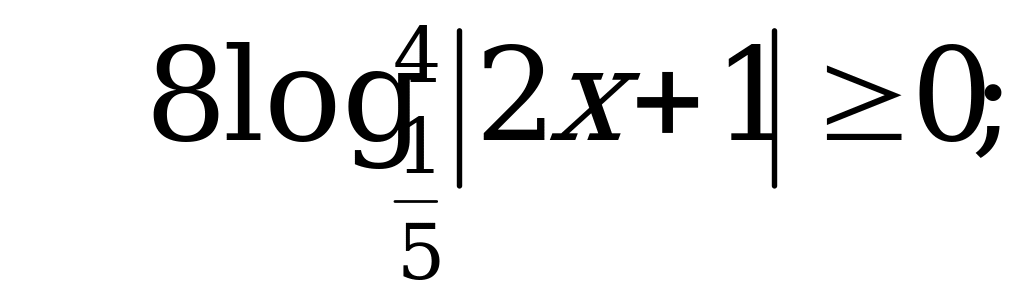
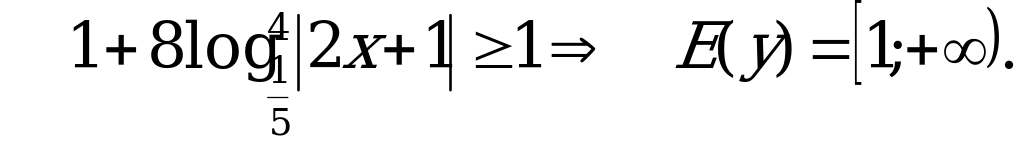
Так как значения функции 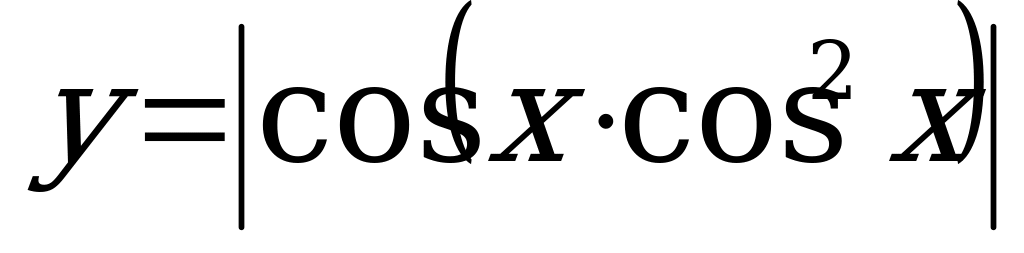 ограничены сверху числом 1, а значения функции
ограничены сверху числом 1, а значения функции  ограничены снизу тем же числом 1, то ясно, что
ограничены снизу тем же числом 1, то ясно, что 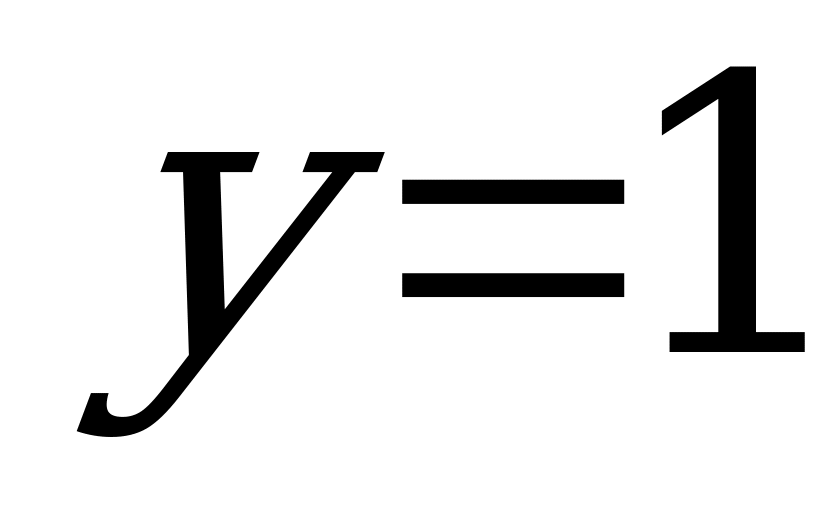 , поэтому:
, поэтому:
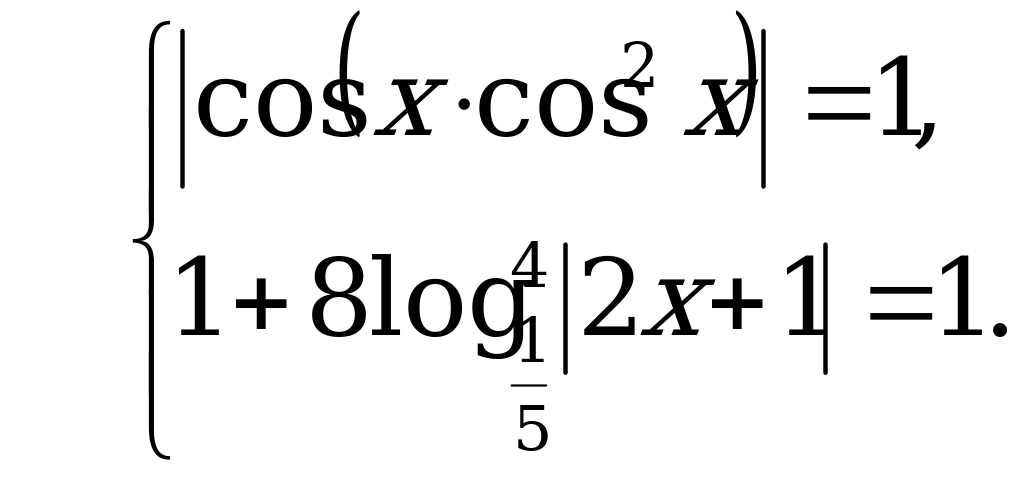
Решим более простое уравнение:
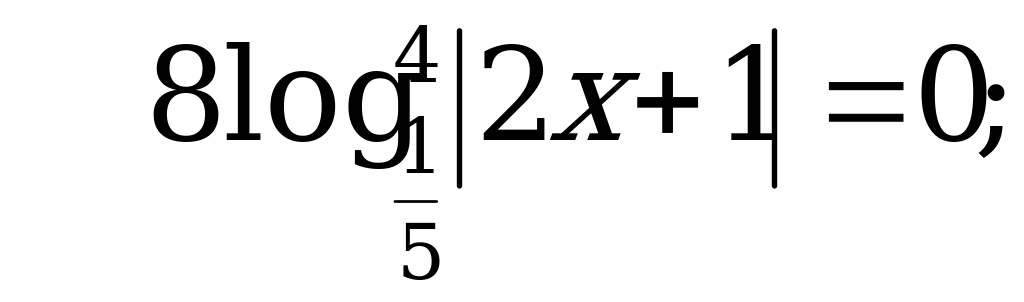
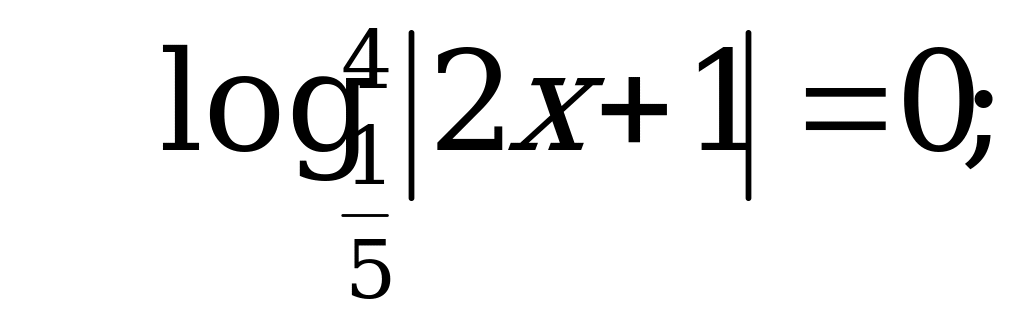
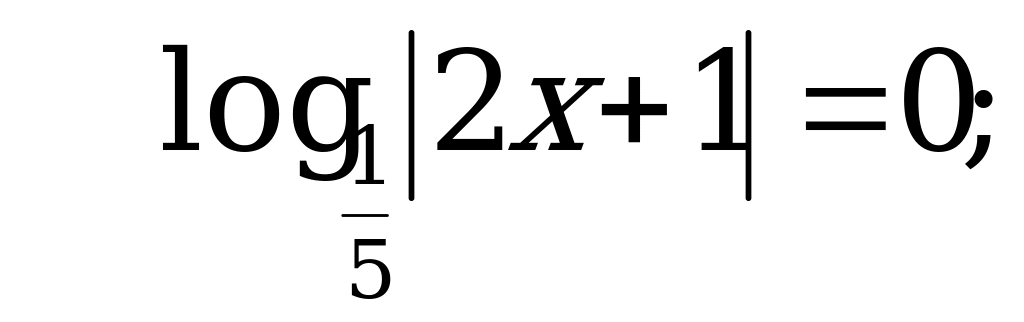
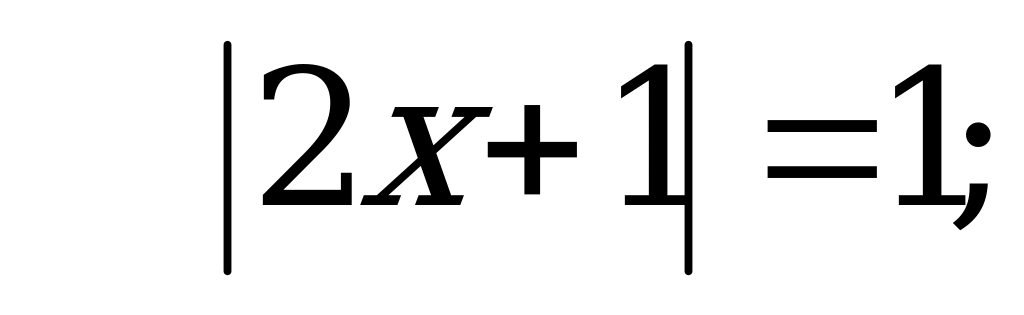
 или
или 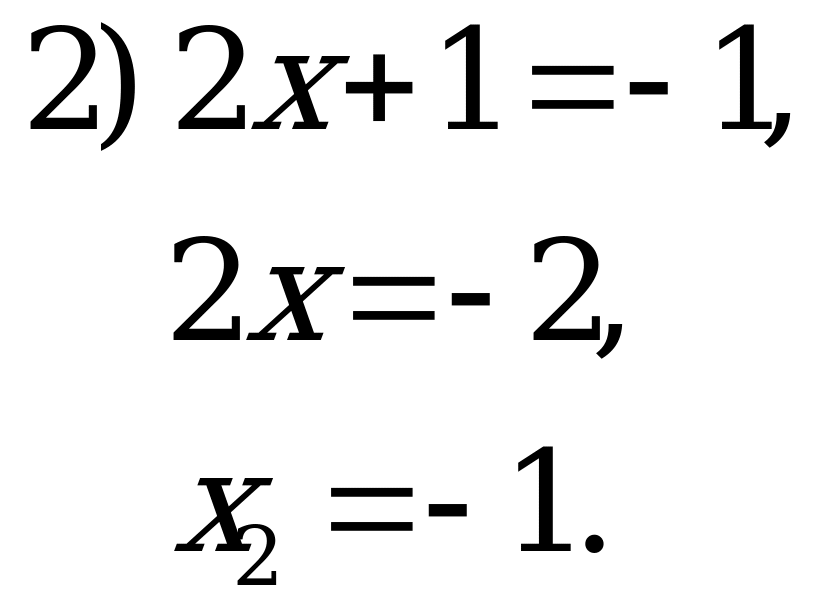
Если 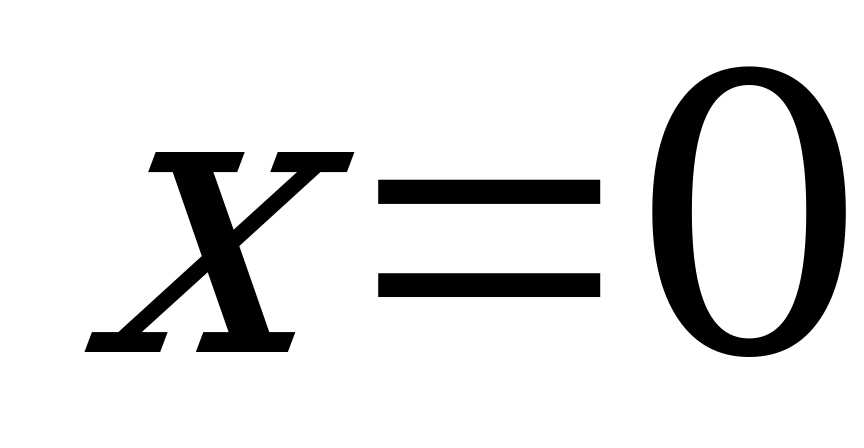 , то
, то 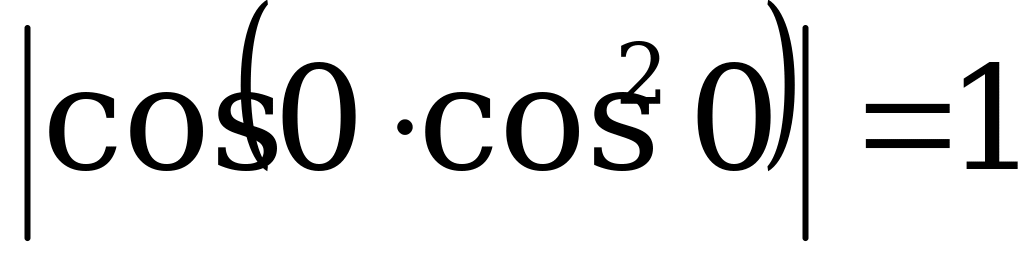 – верно.
– верно.
Если 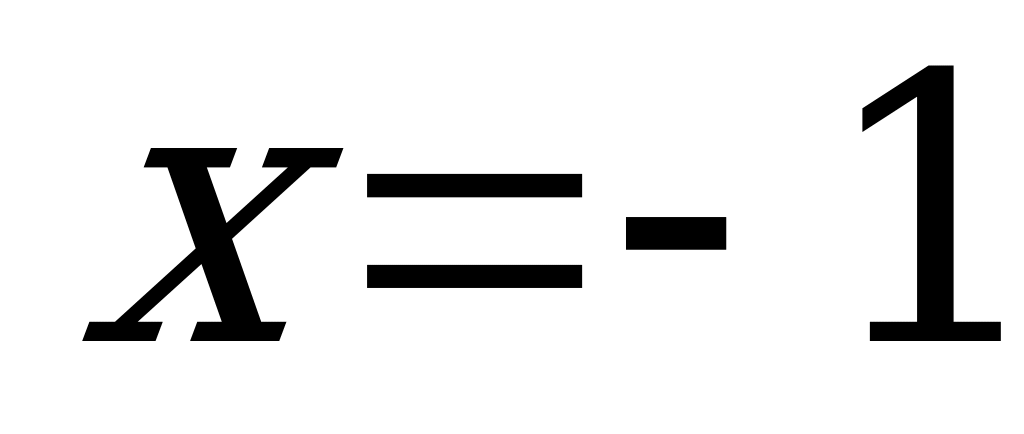 , то
, то 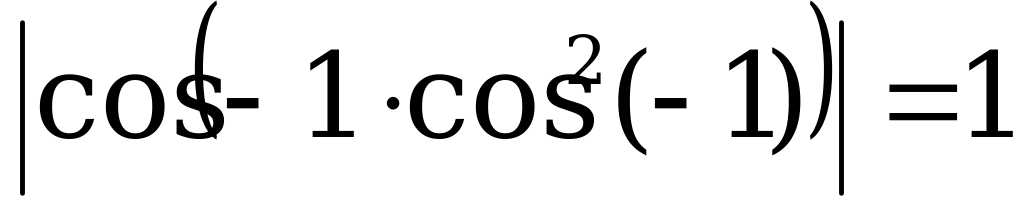 – неверно.
– неверно.
Решение системы, а значит и уравнения 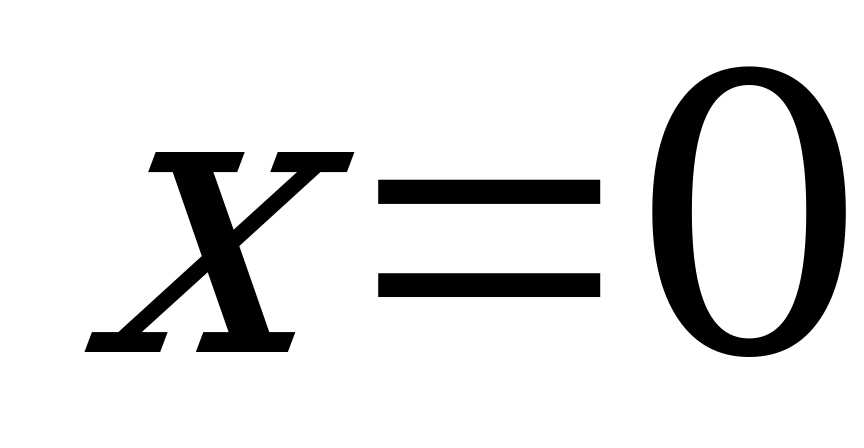 .
.
Ответ: 0.
С3: Найдите целые корни уравнения 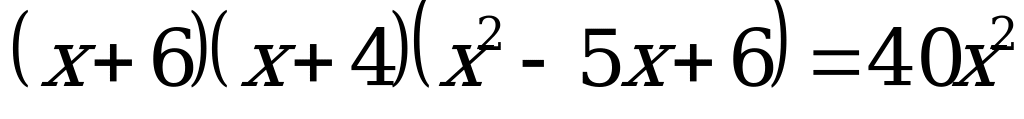 .
.
Решение:
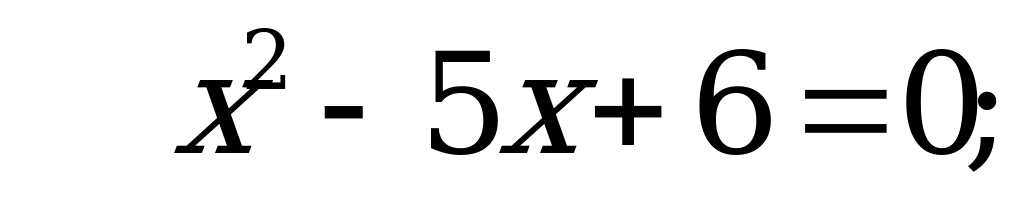
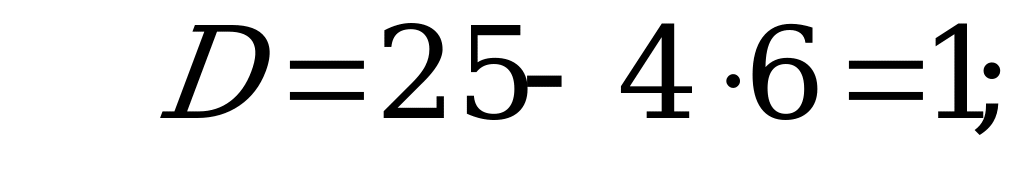
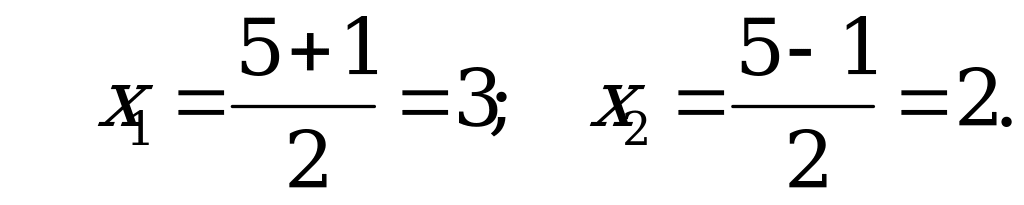
Значит 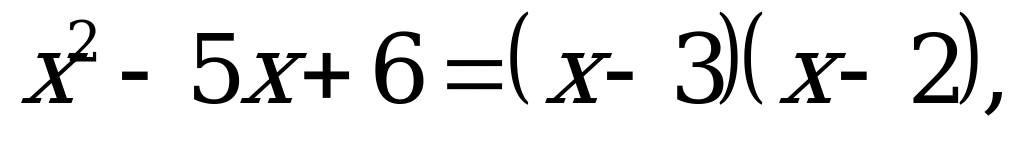 получим:
получим:
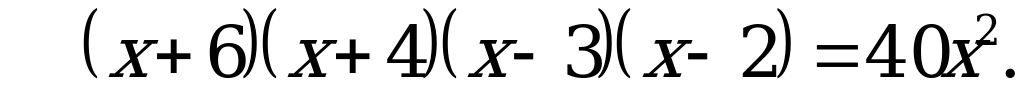
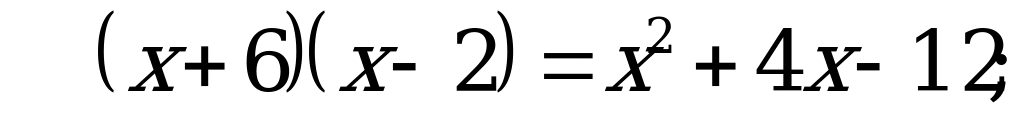
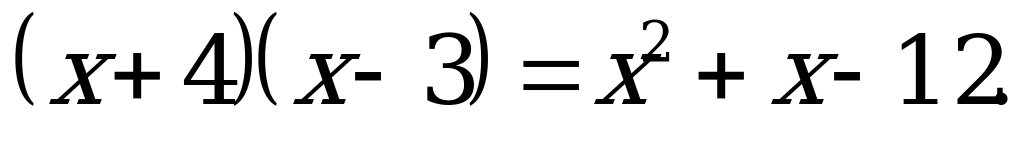
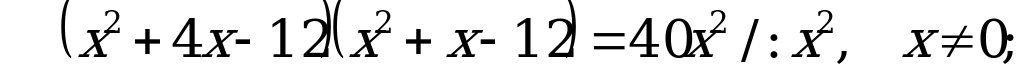
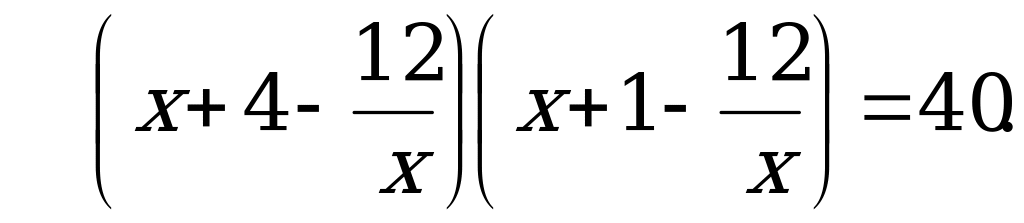
Пусть 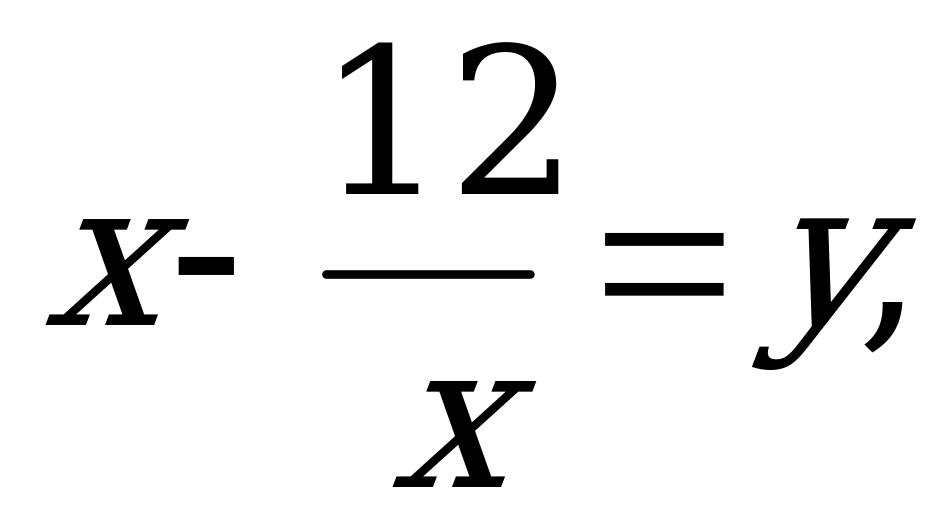 тогда
тогда 
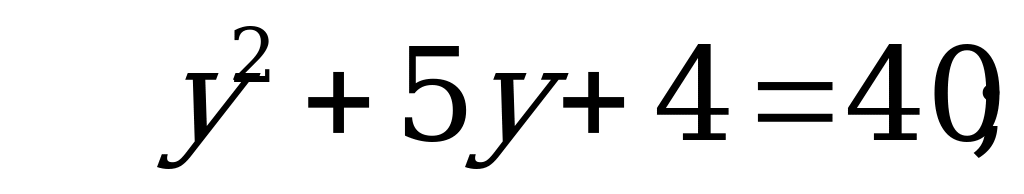
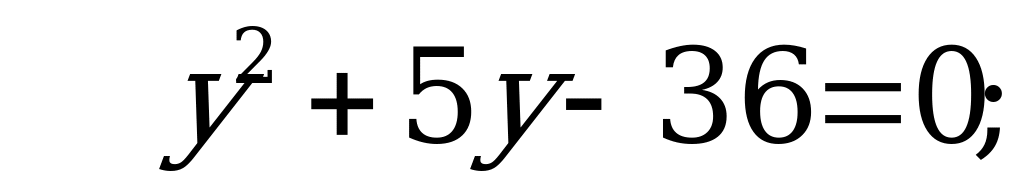
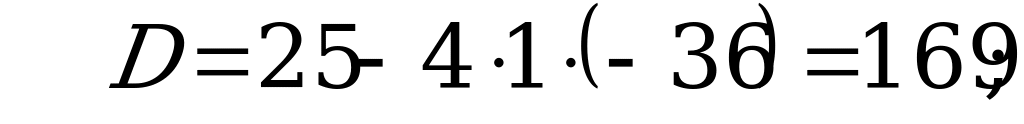
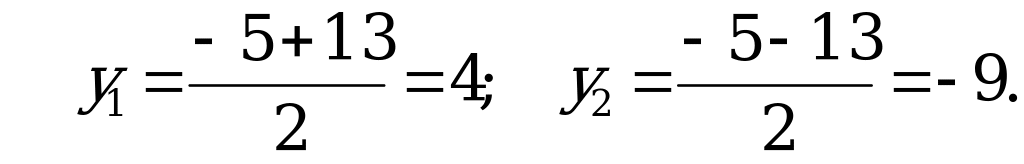
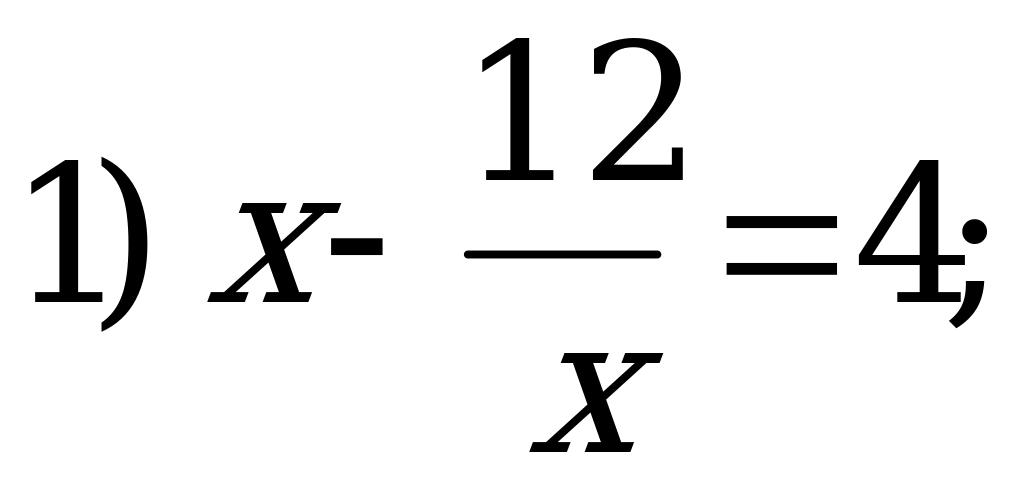
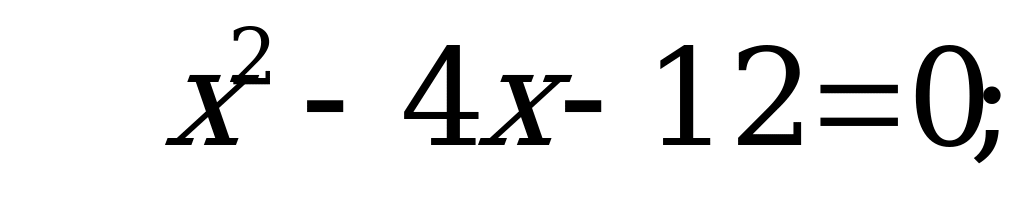
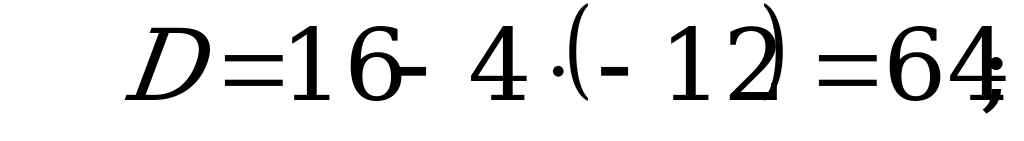
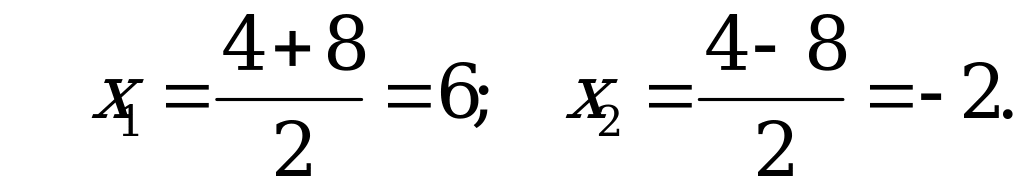
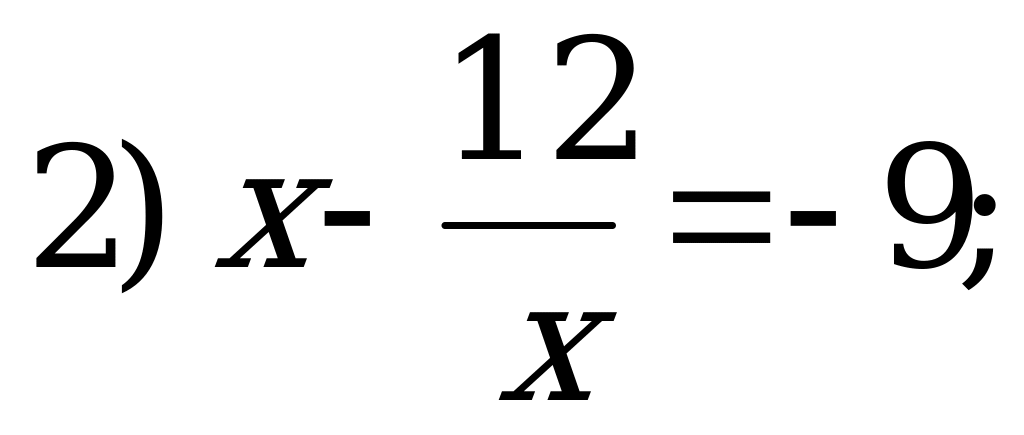
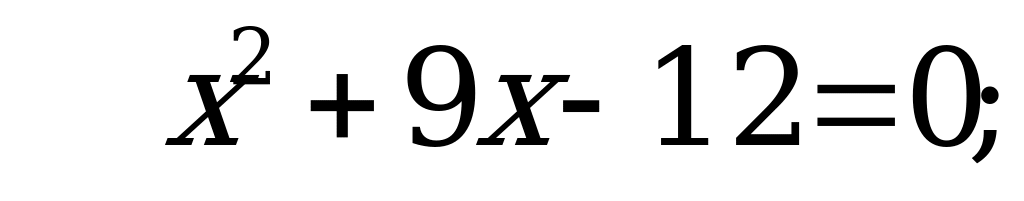
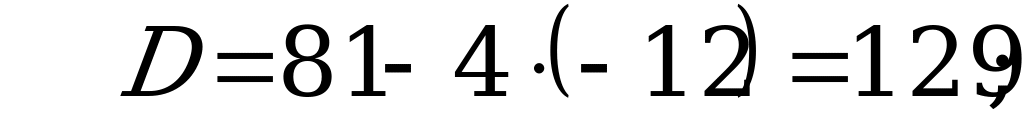
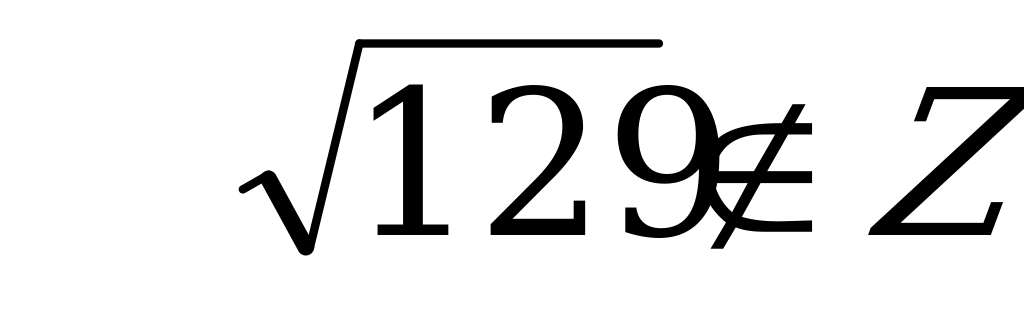 , значит корни не целые числа.
, значит корни не целые числа.
Ответ: – 2; 6.
5. Итоги урока.
6. Домашнее задание.
Задания из ЕГЭ (приложение).
Урок 99 – 101.
Решение ЕГЭ.
Цели урока: Повторение материала по всем темам, подготовка к экзамену.
Ход урока.
1. Организационный момент.
2. Задания ЕГЭ.
Лучше задания напечатать каждому учащемуся на индивидуальном листе.
ТЕСТЫ
ТРЕНИРОВАЧНЫЙ ВАРИАНТ ЕГЭ. (2003 год.)
Часть 1.
А1. Упростите выражение 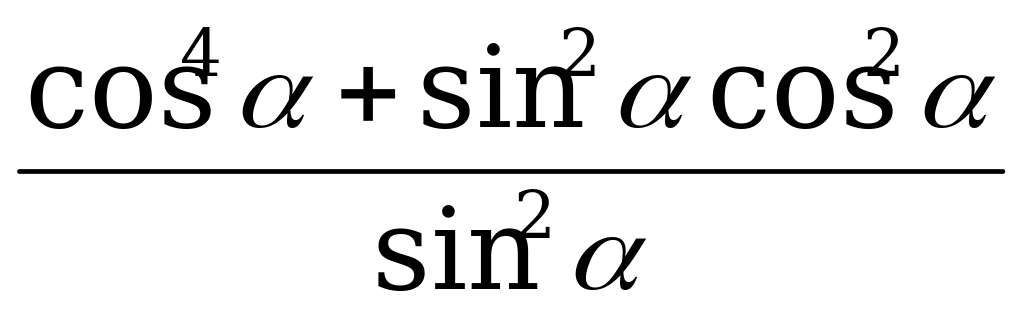 .
.
1) 1; 2) 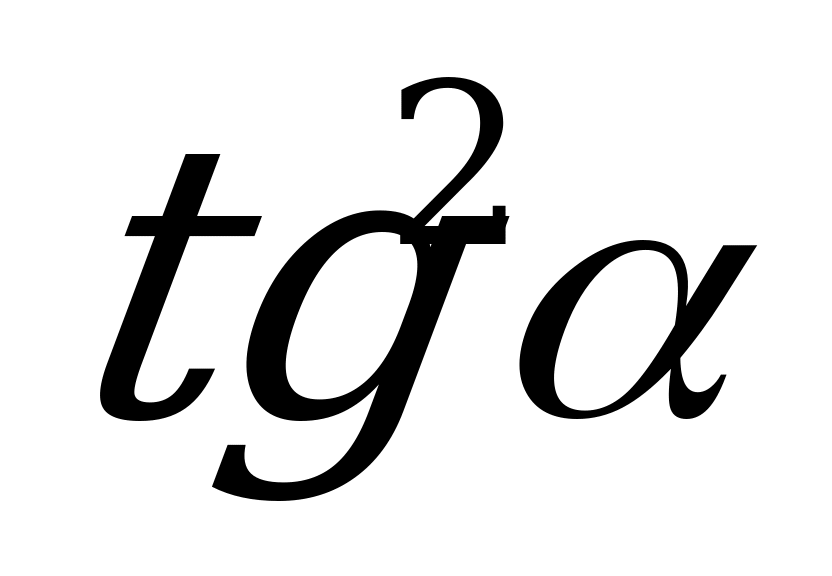 ; 3)
; 3) 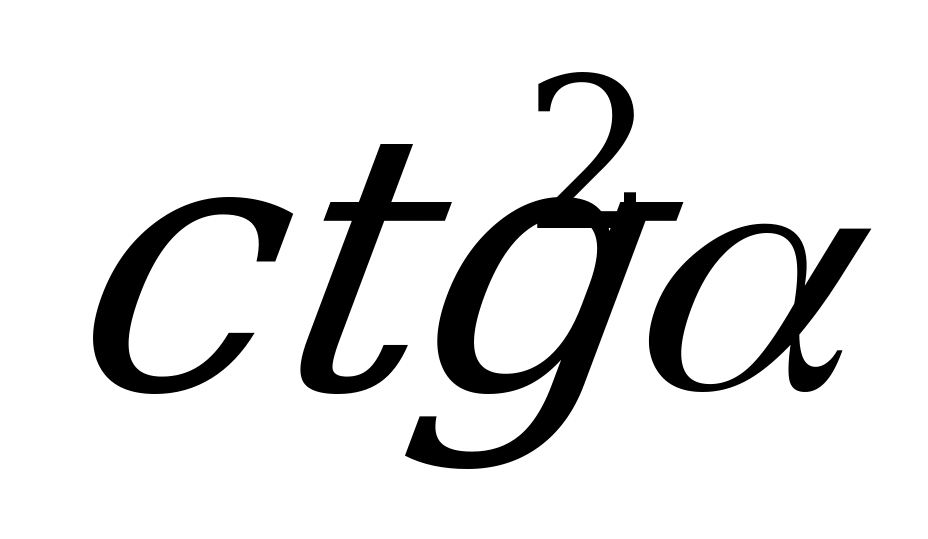 ; 4)
; 4) 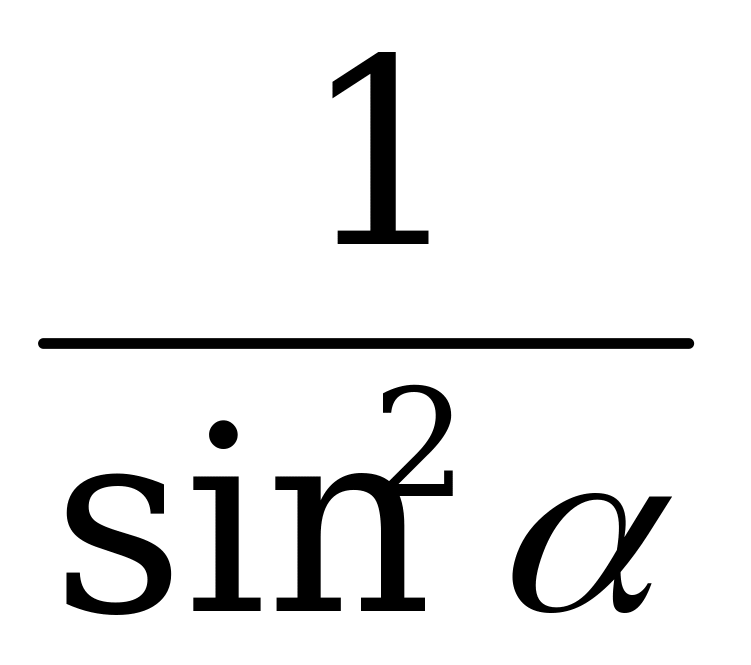 .
.
А2. Представьте выражение 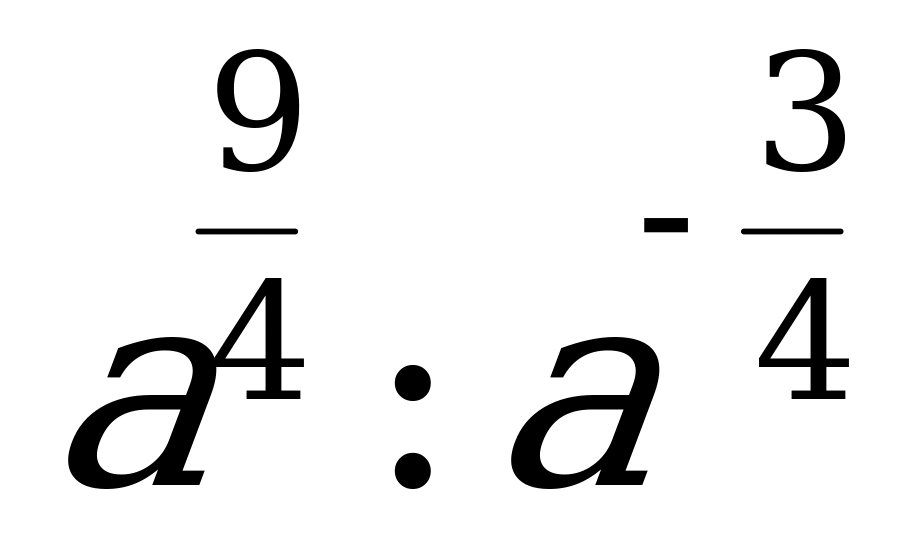 в виде степени.
в виде степени.
1) 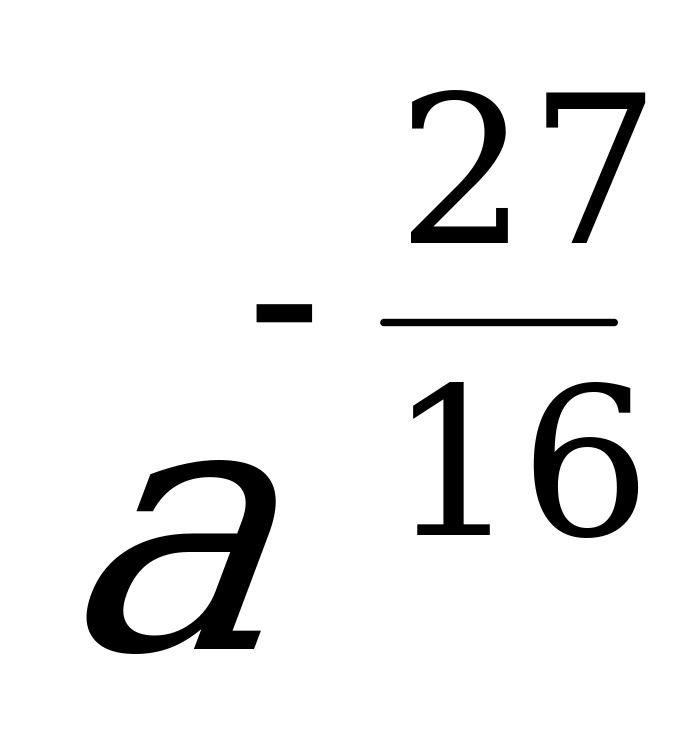 ; 2)
; 2) 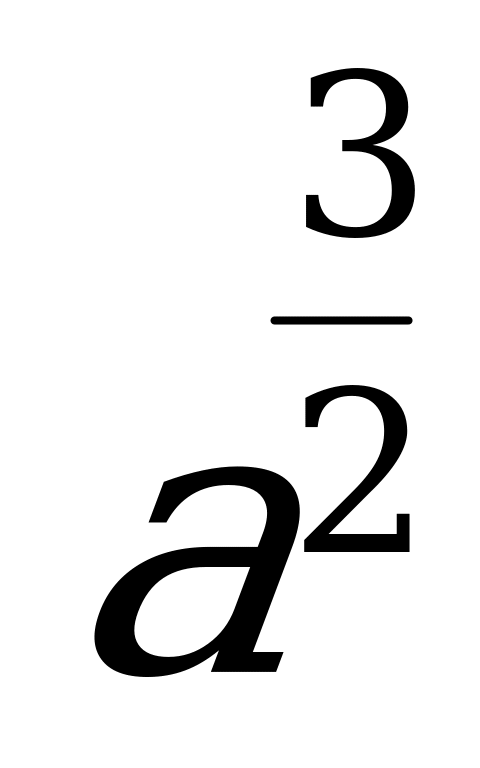 ; 3)
; 3) 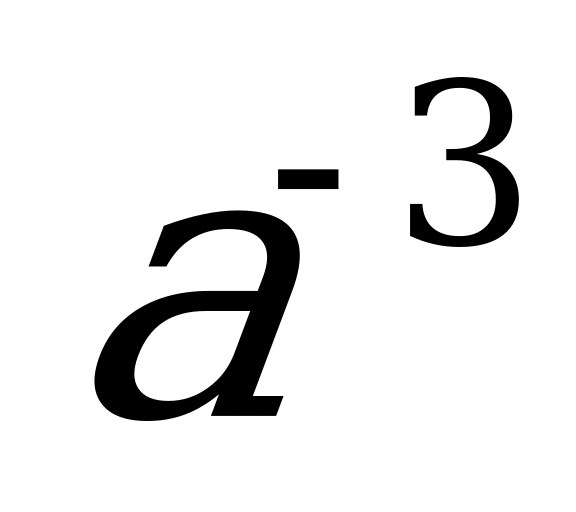 ; 4)
; 4) 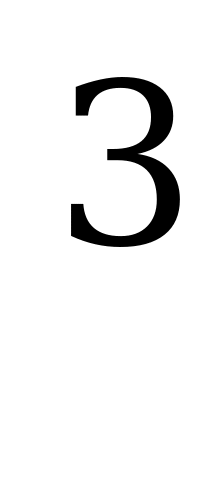 .
.
А3. Вычислите 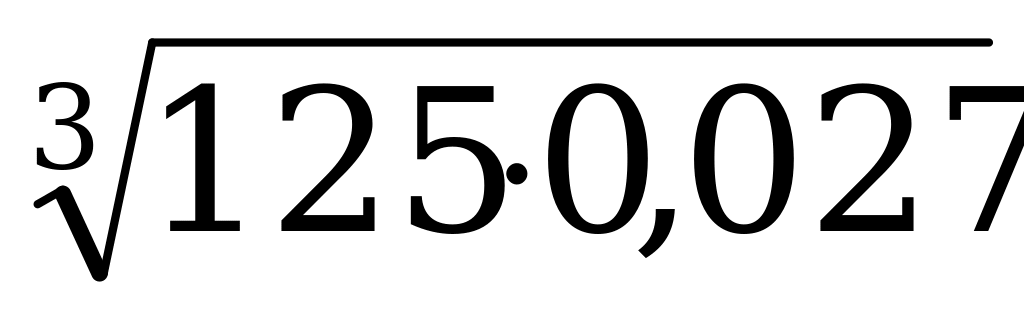 .
.
1) 1,5; 2) 15; 3)0,015; 4) 0,15.
А4. Найдите значение выражения 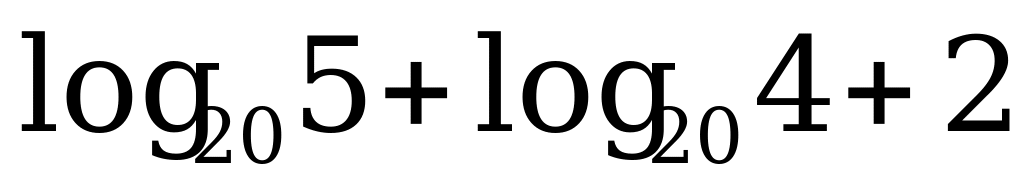 .
.
1) 11; 2) 2; 3) 3; 4) 22.
А5. Найдите все решения уравнения 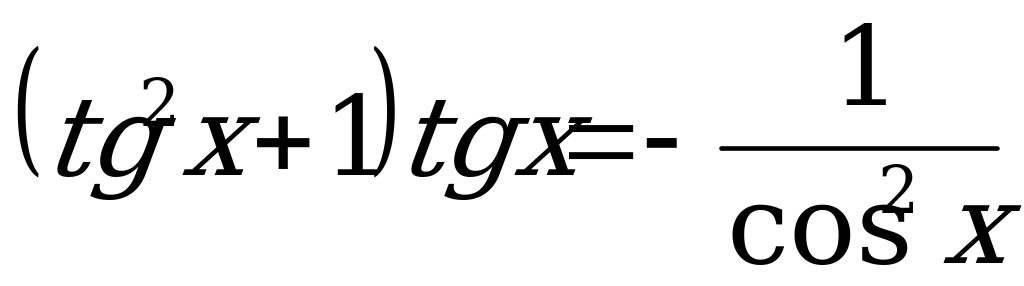 .
.
1) 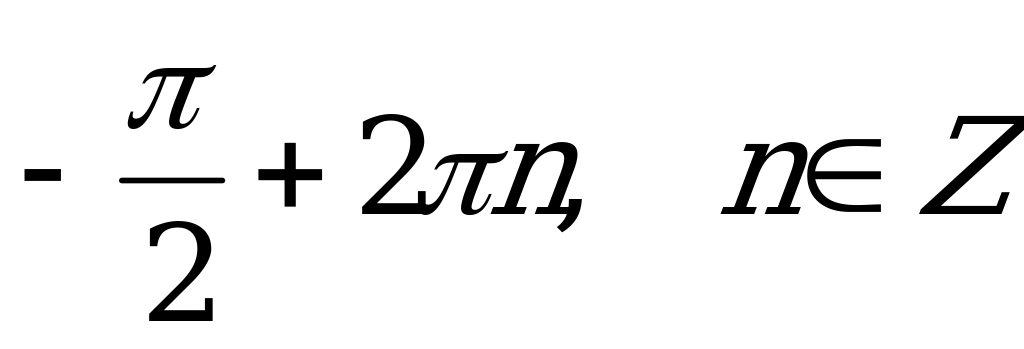 ; 2)
; 2) 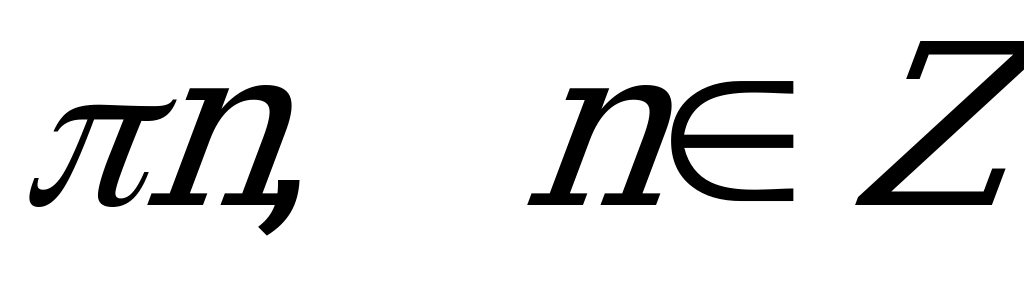 ;
;
3) 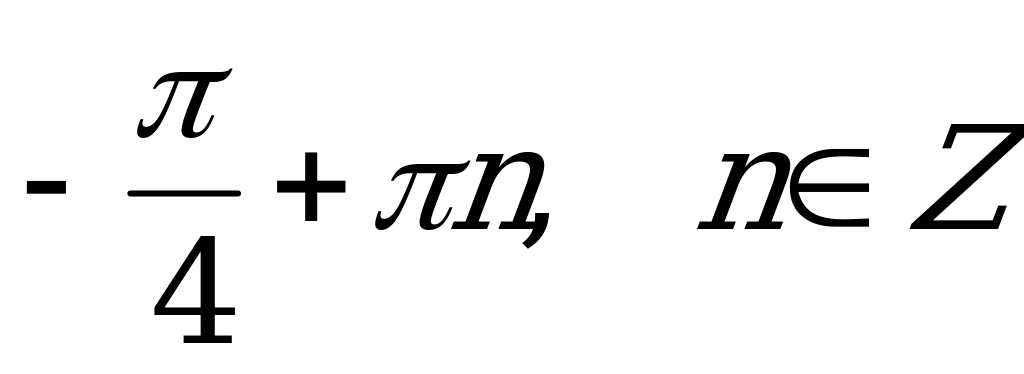 ; 4)
; 4) 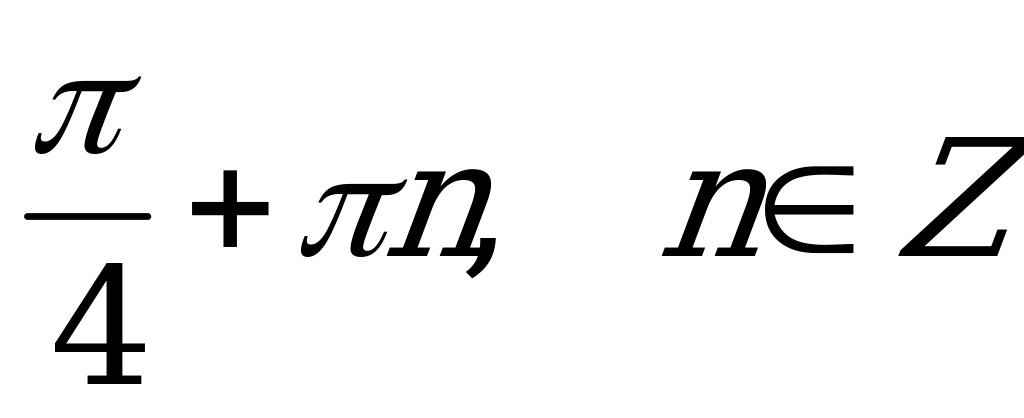 .
.
А6. Укажите промежуток, которому принадлежит корень уравнения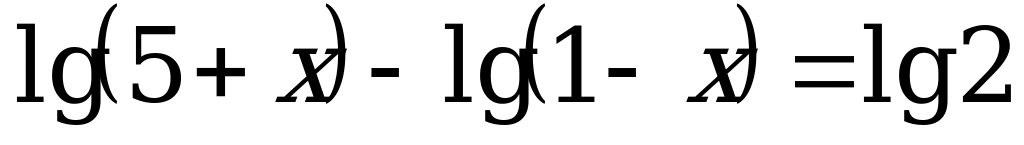 .
.
1) 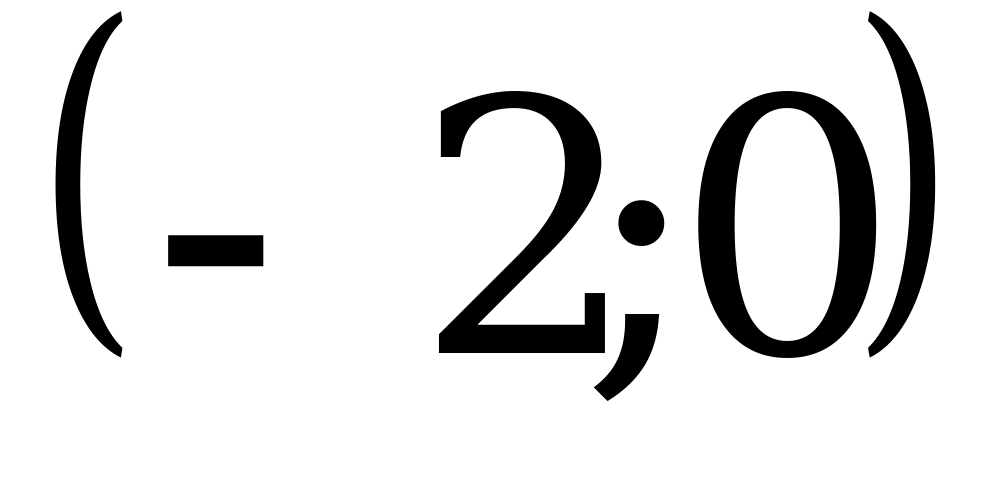 ; 2)
; 2) 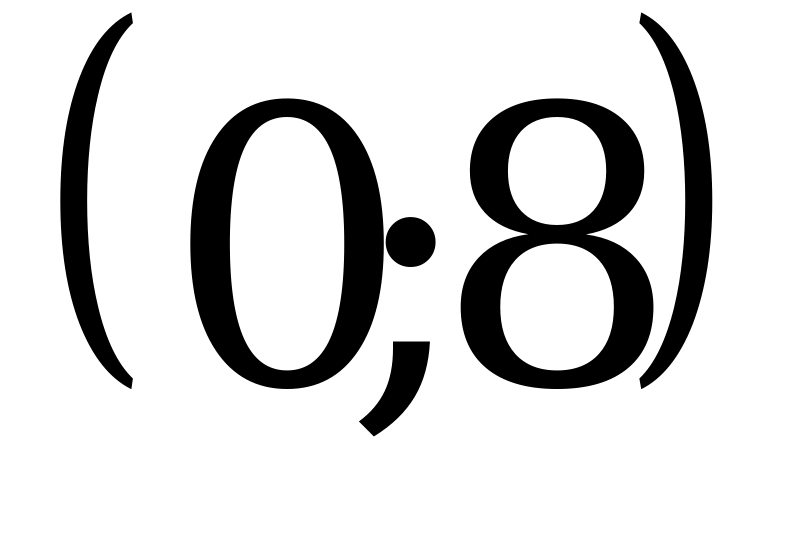 ; 3)
; 3) 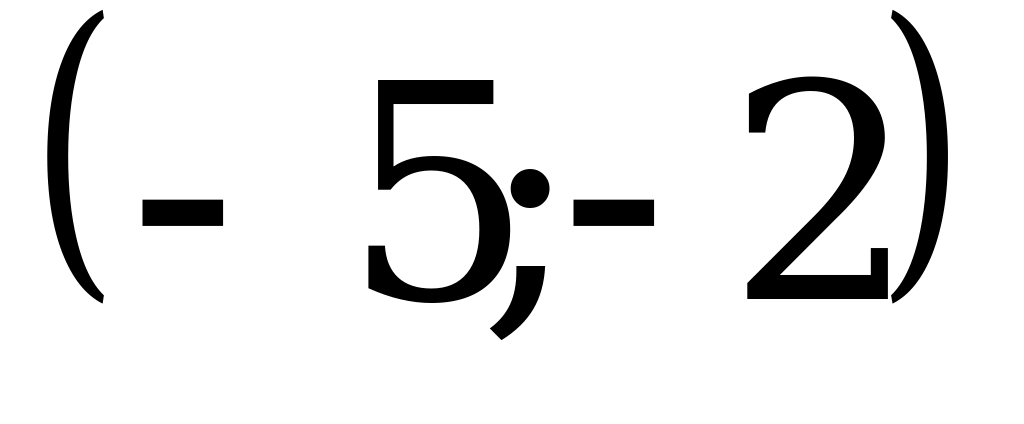 ; 4)
; 4) 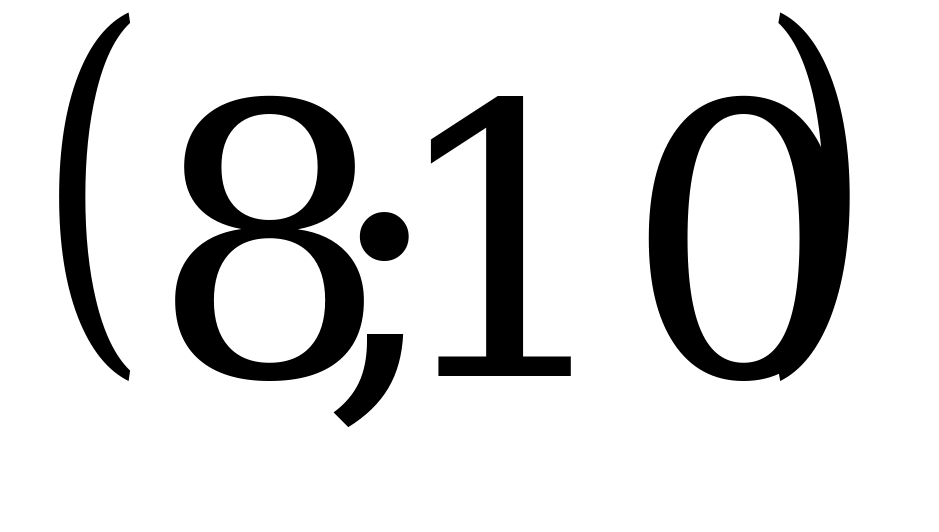 .
.
А7. Решите неравенство 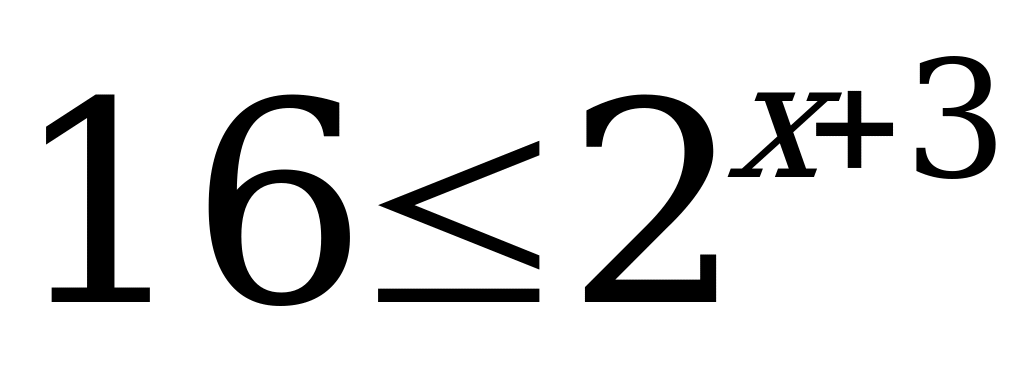 .
.
1) – 3; 2) 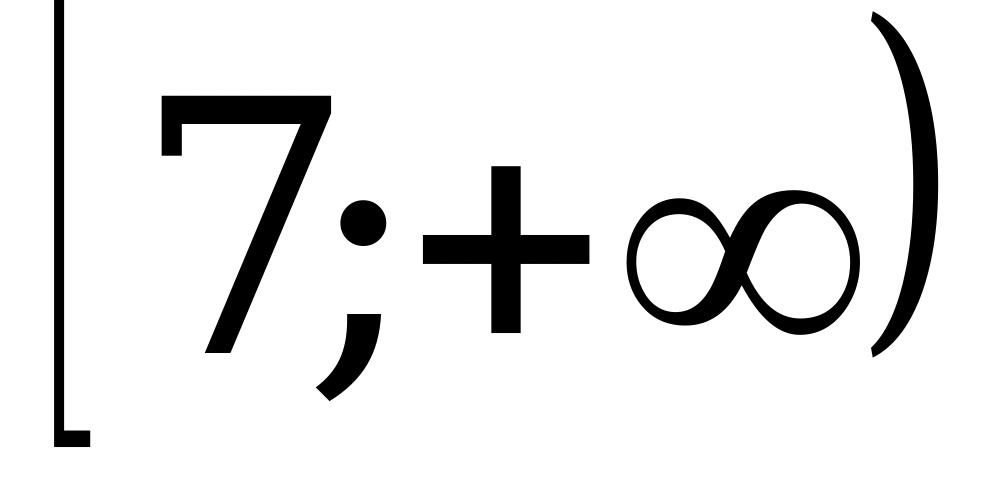 ; 3)
; 3) 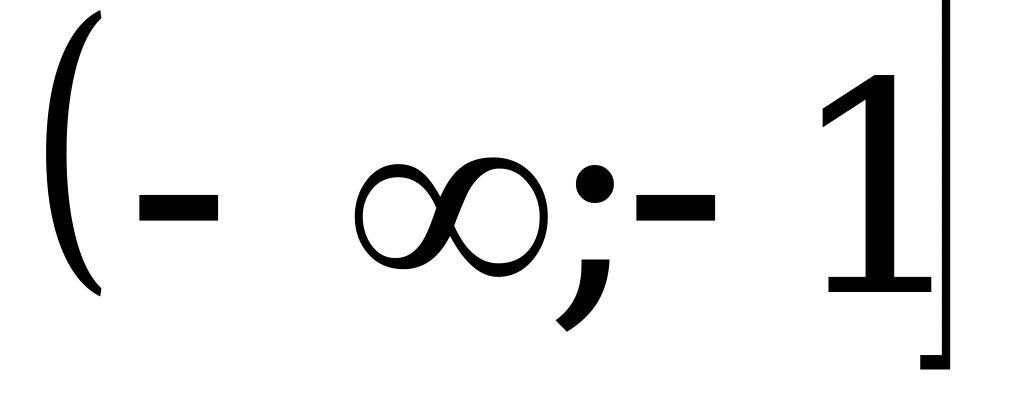 ; 4)
; 4) 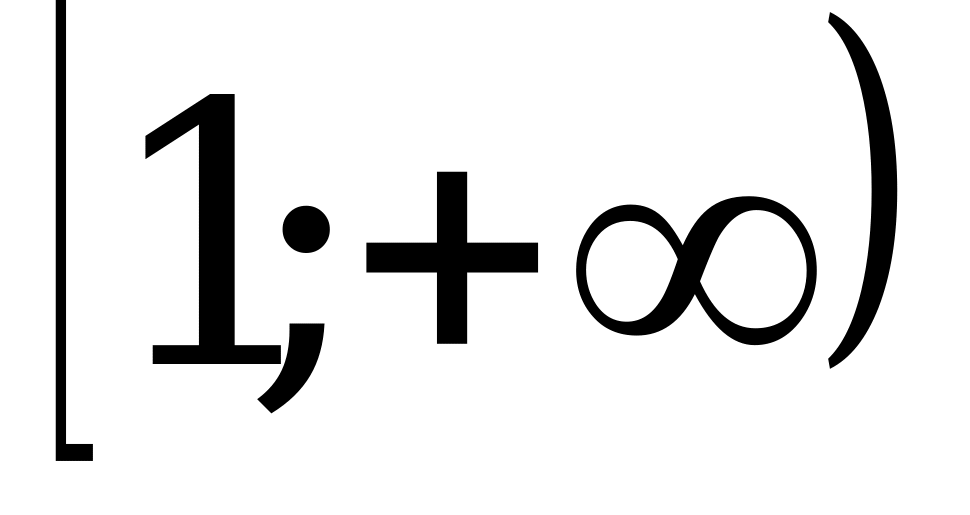 .
.
А8. Определите число целых решений неравенства 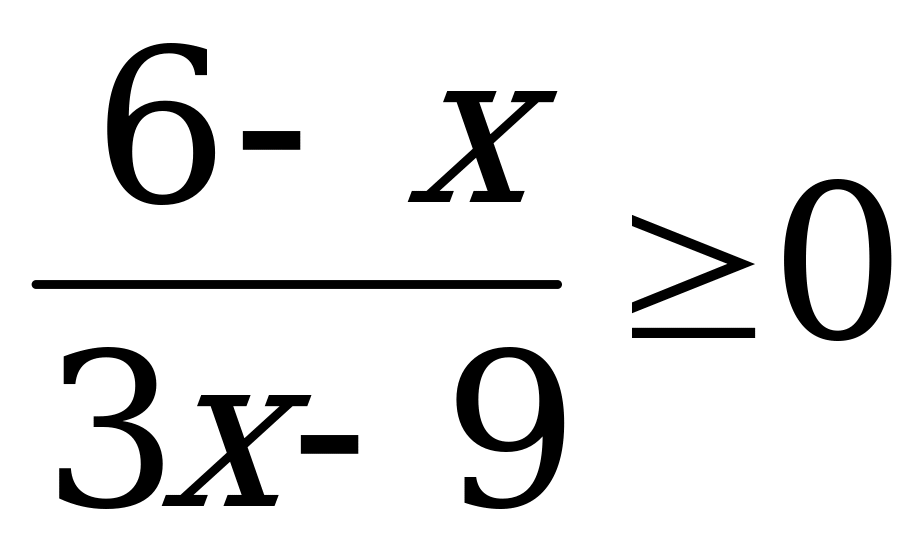 .
.
1) 1; 2) 2; 3) 3; 4) 4.
А9. Укажите промежуток, которому принадлежат корни уравнения 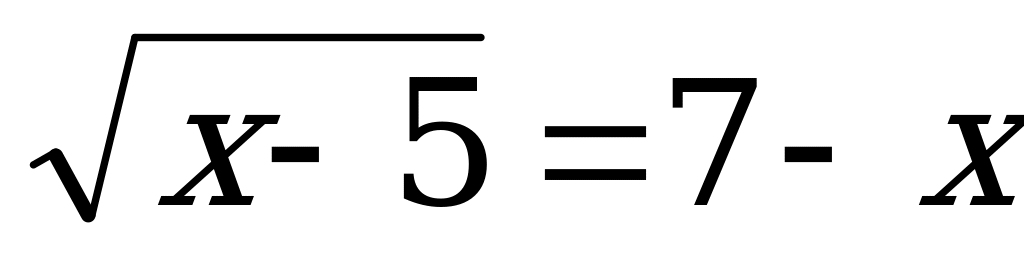 .
.
1) 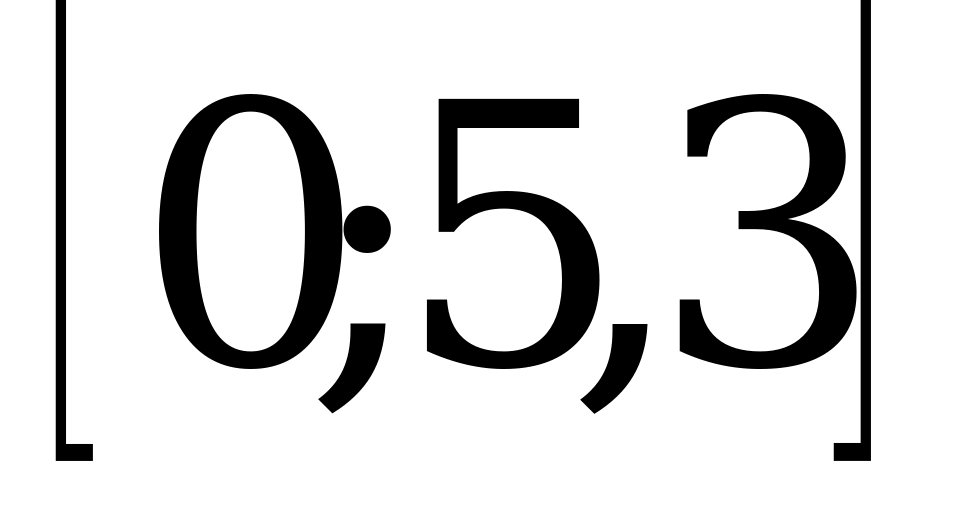 ; 2)
; 2) 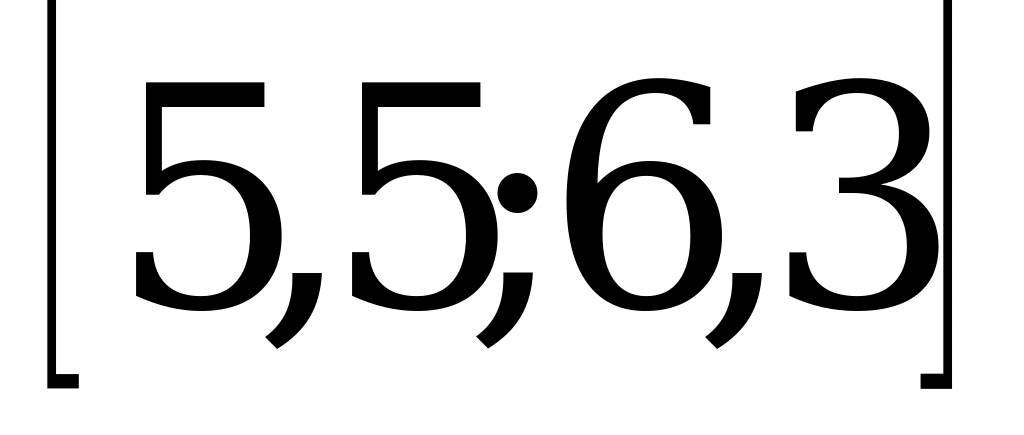 ; 3)
; 3) 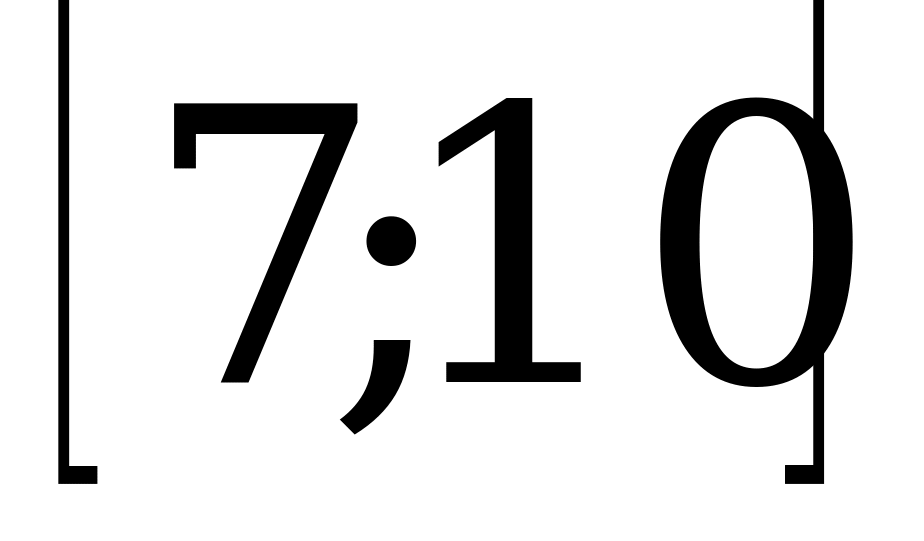 ; 4)
; 4) 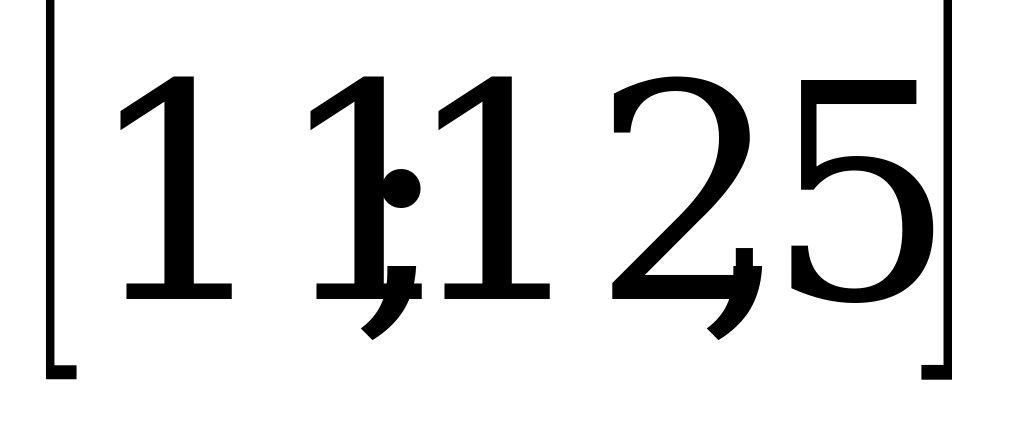 .
.
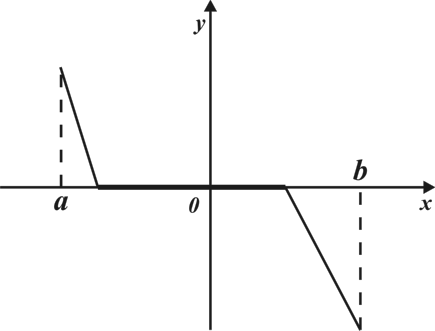
А10. Функция задана графиком. Укажите область определения этой функции.
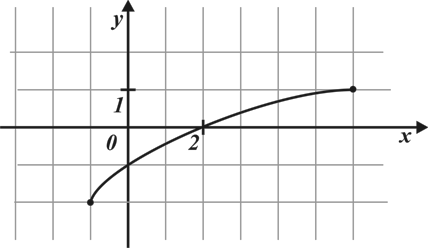
1) 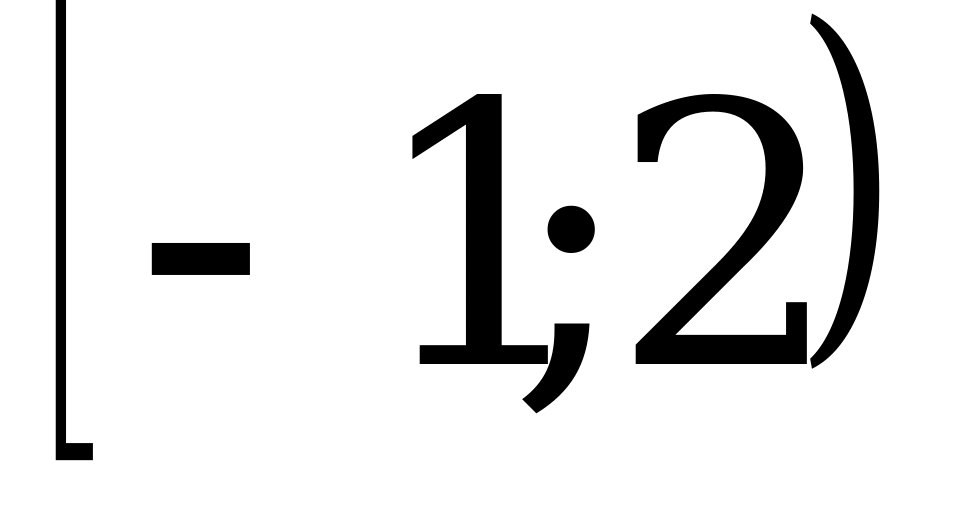 ; 2)
; 2) 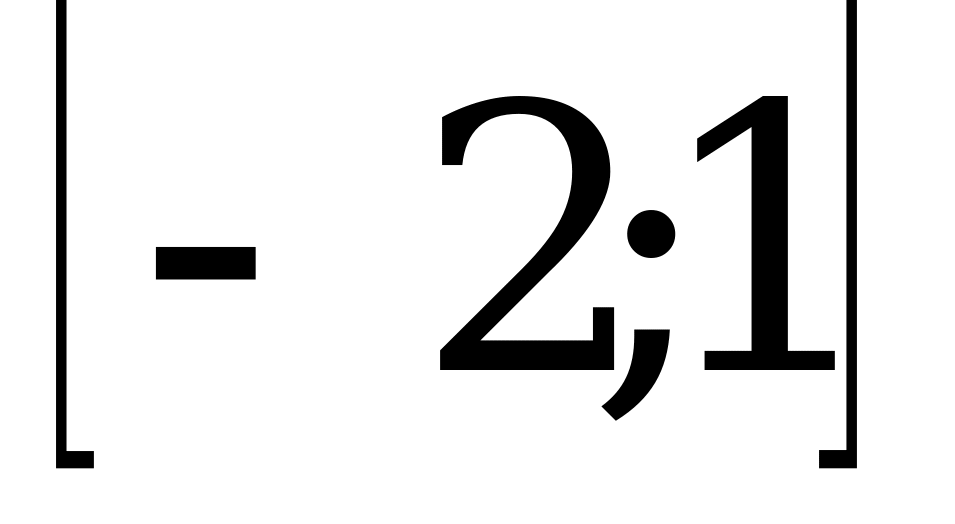 ; 3)
; 3) 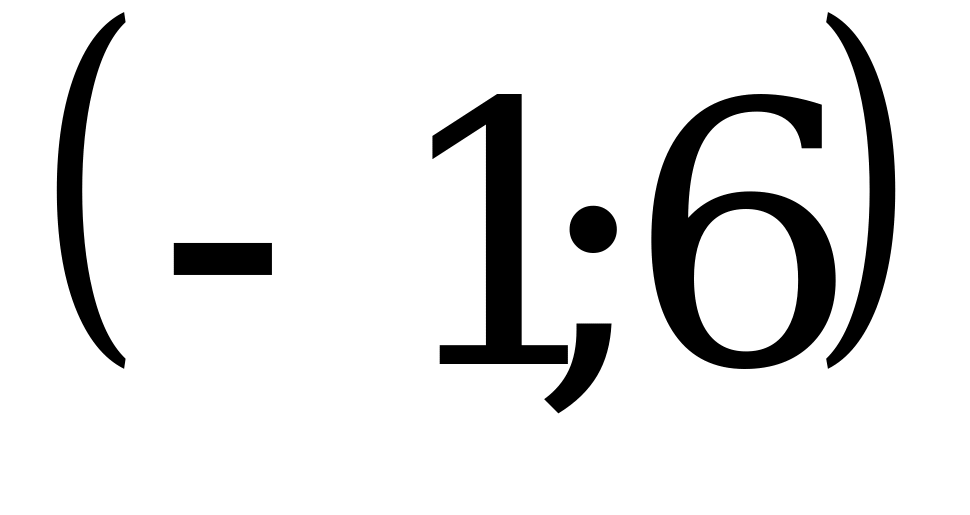 ; 4)
; 4) 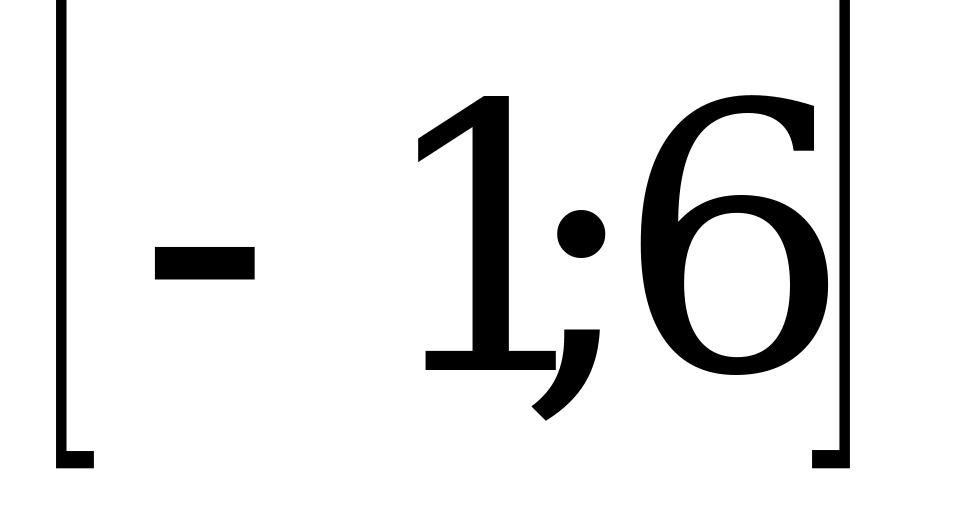 .
.
А11. Найдите область определения функции 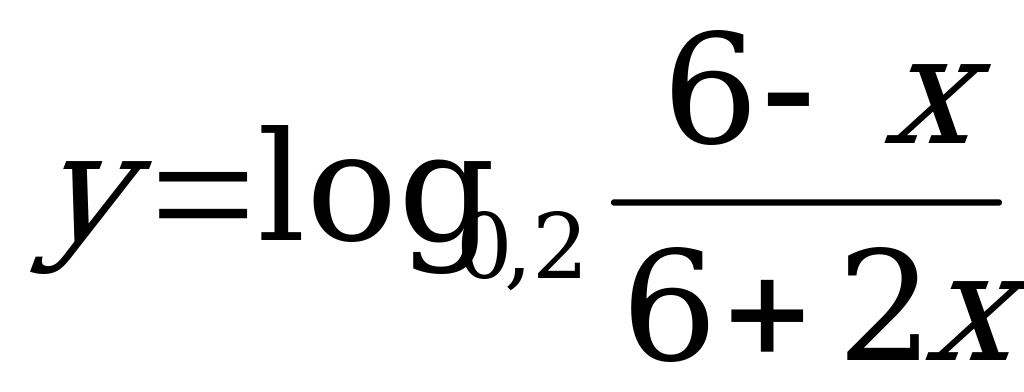 .
.
1)  ; 2)
; 2) 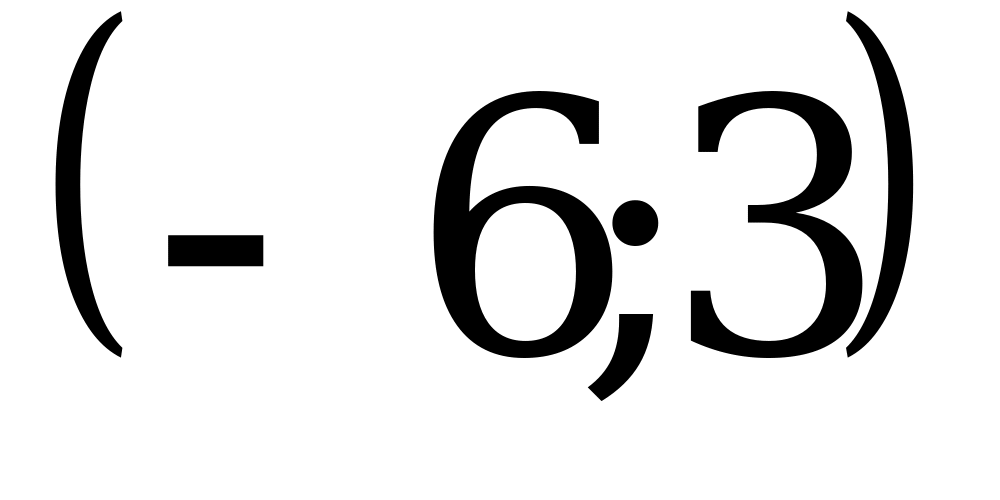 ; 3)
; 3) 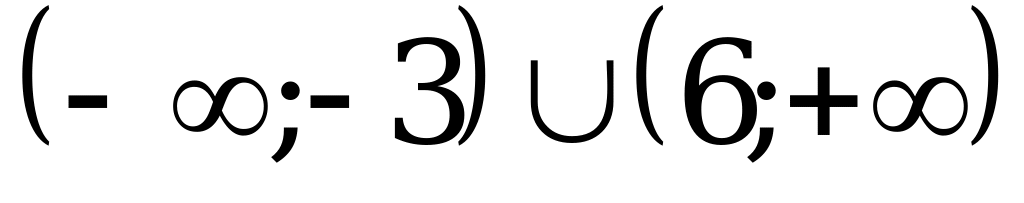 ; 4)
; 4) 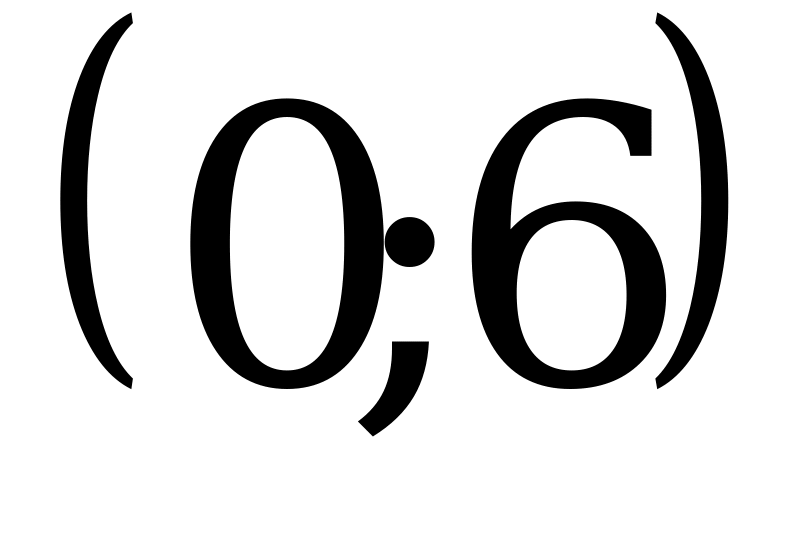 .
.
А12. Найдите множество значений функции 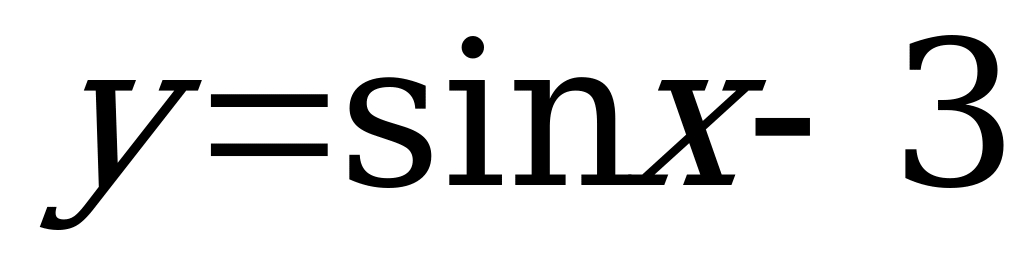 .
.
1) 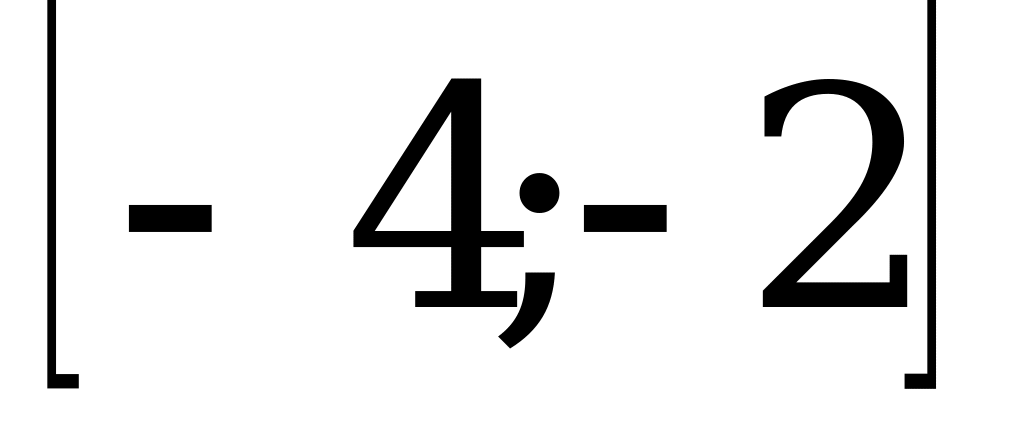 ; 2)
; 2) 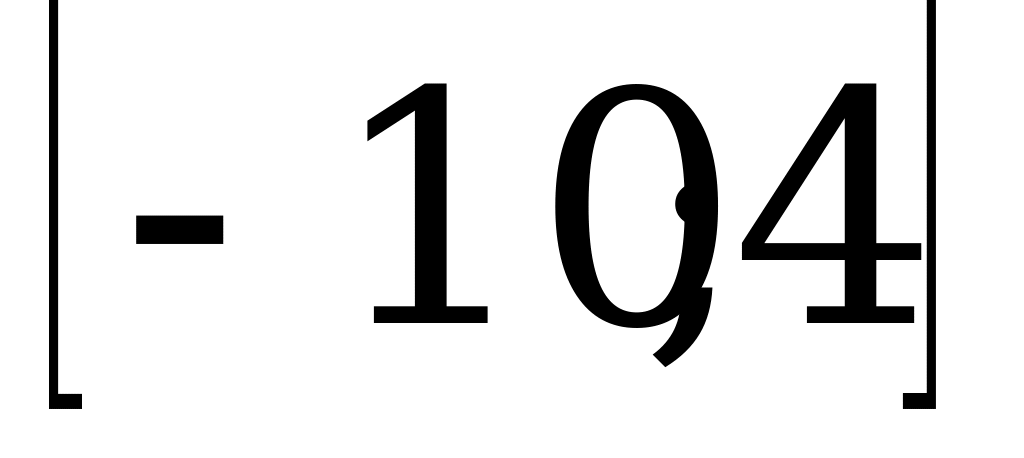 ; 3)
; 3) 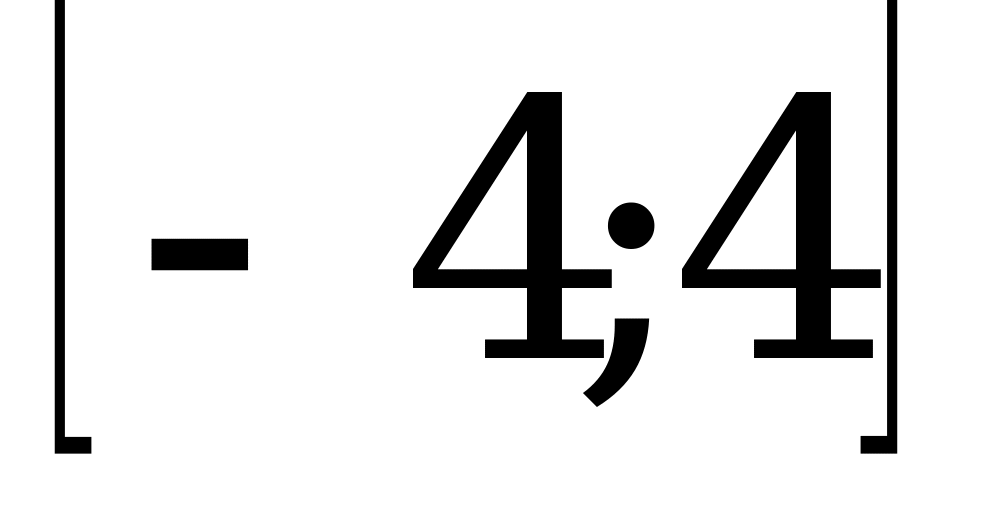 ; 4)
; 4) 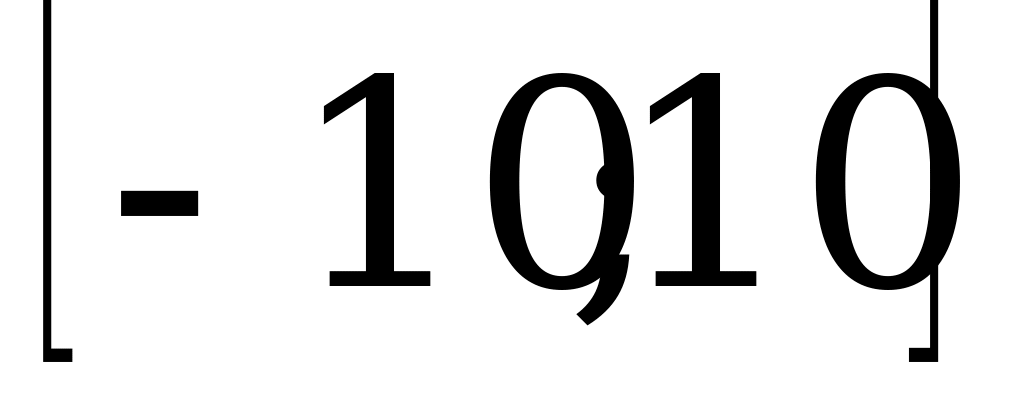 .
.
А13. График, какой из перечисленных функций изображен на рисунке?
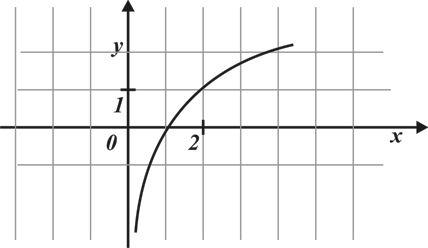
1) 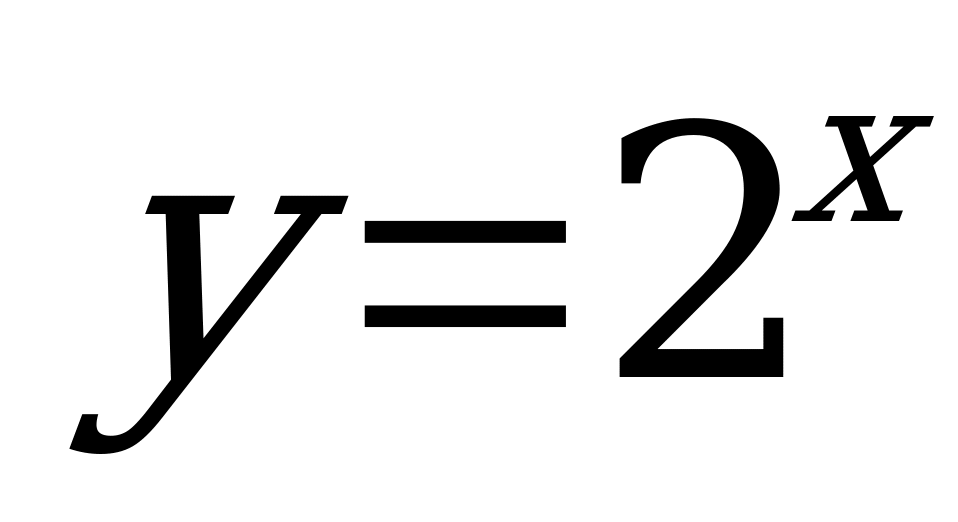 ; 2)
; 2) 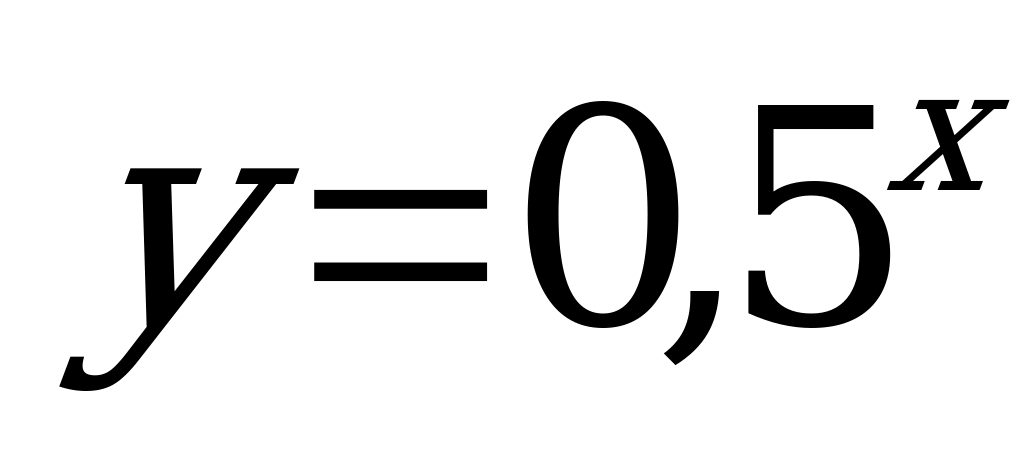 ; 3)
; 3) 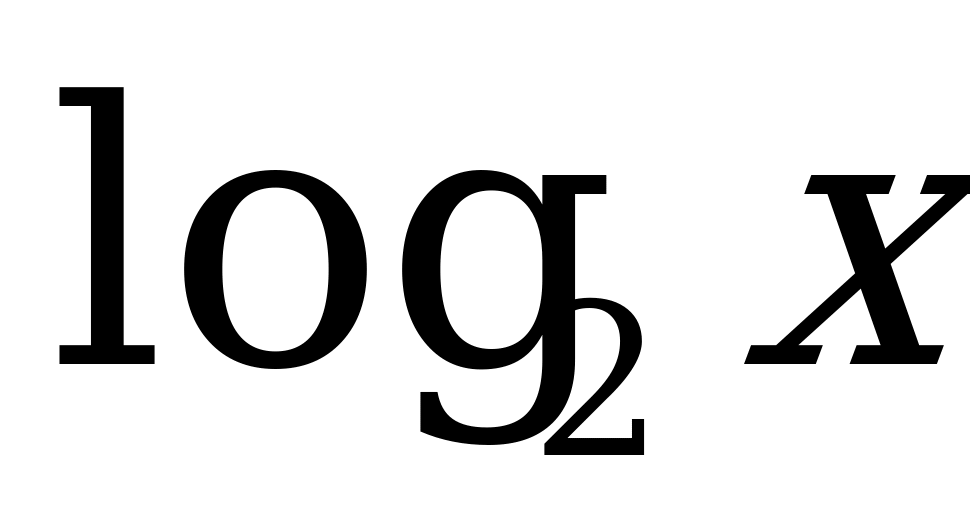 ; 4)
; 4) 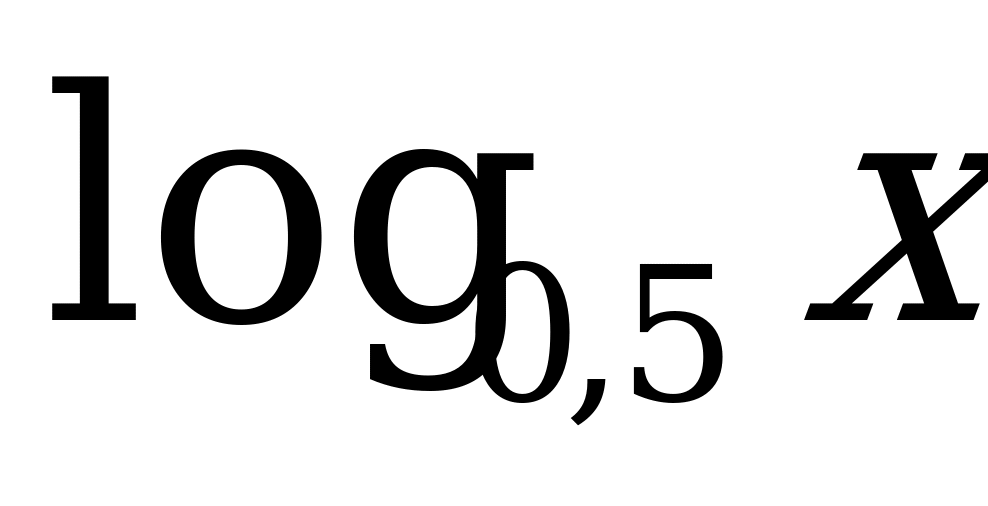 .
.
А14. Найдите производную функции 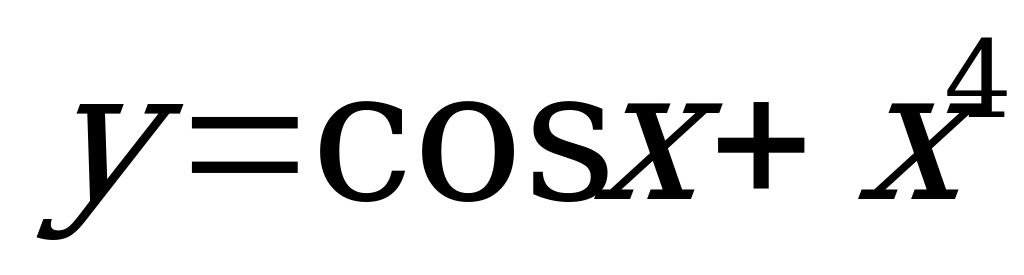 .
.
1) 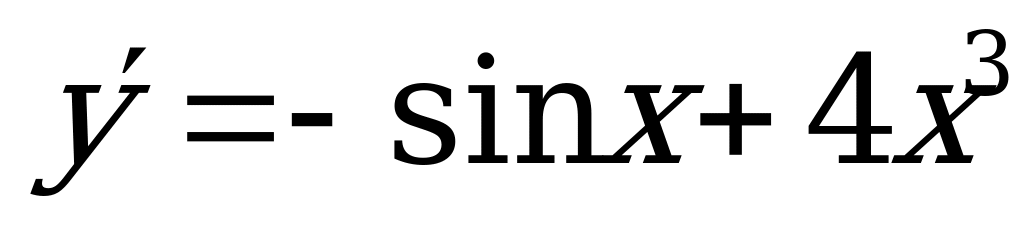 ; 2)
; 2) 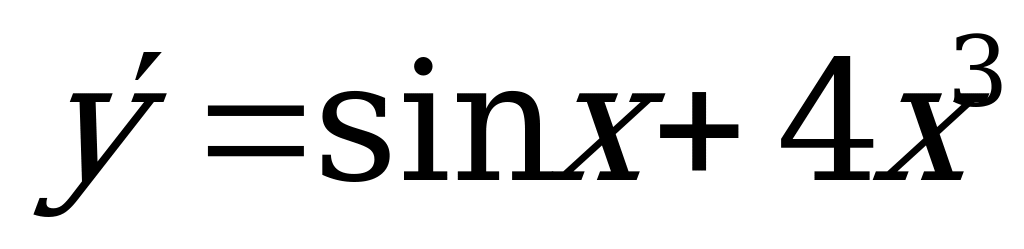 ;
;
3) 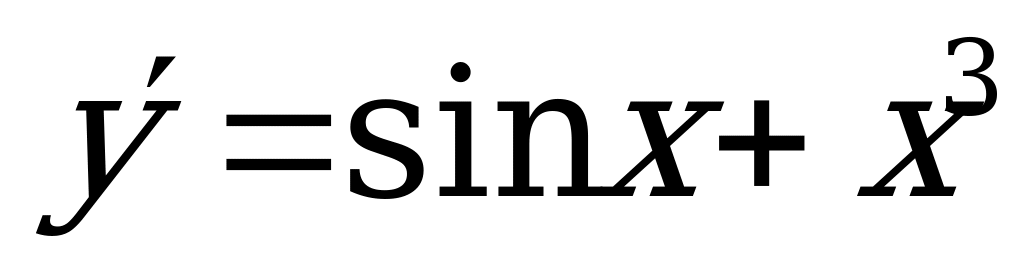 ; 4)
; 4) 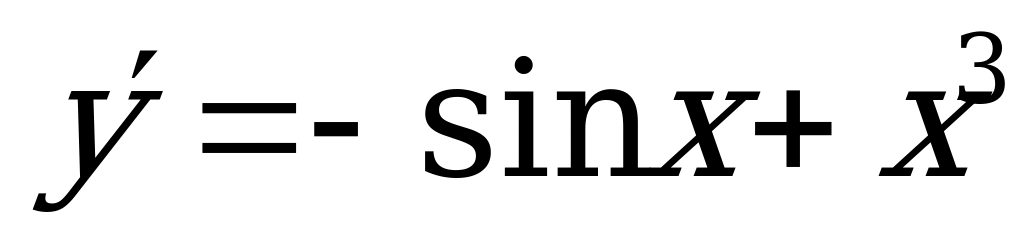 .
.
А15. Найдите первообразную  функции
функции 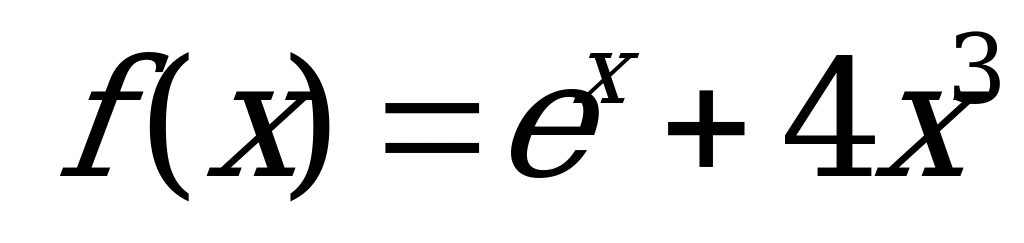 , если известно, что
, если известно, что 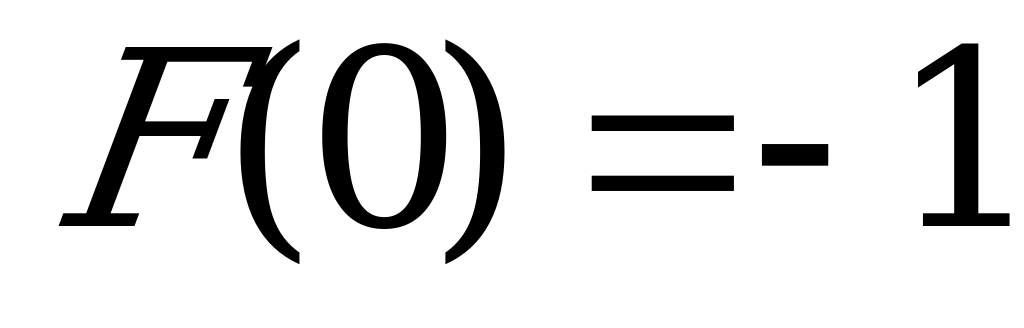 .
.
1) 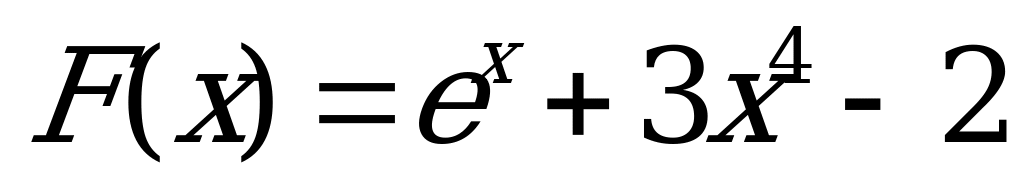 ; 2)
; 2) 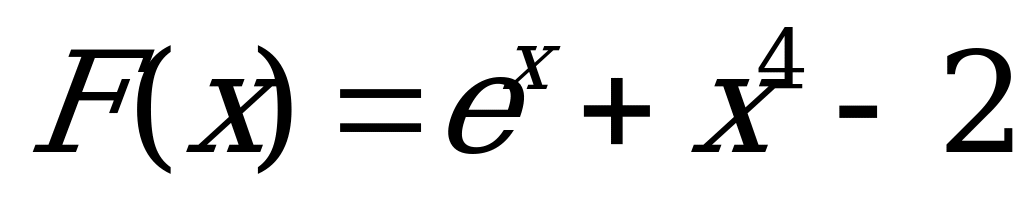 ;
;
3) 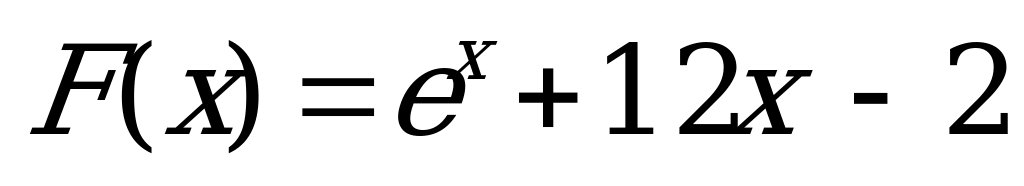 ; 4)
; 4) 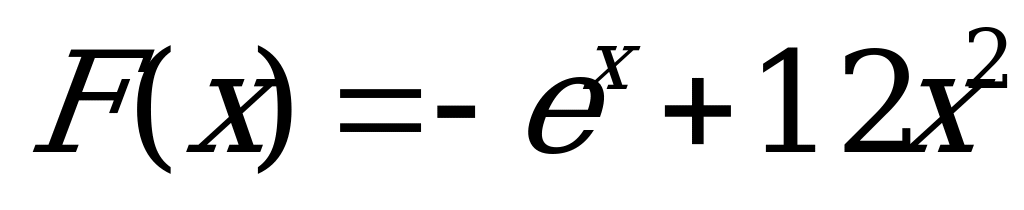 .
.
А14. Найдите угловой коэффициент касательной, проведенной к графику функции 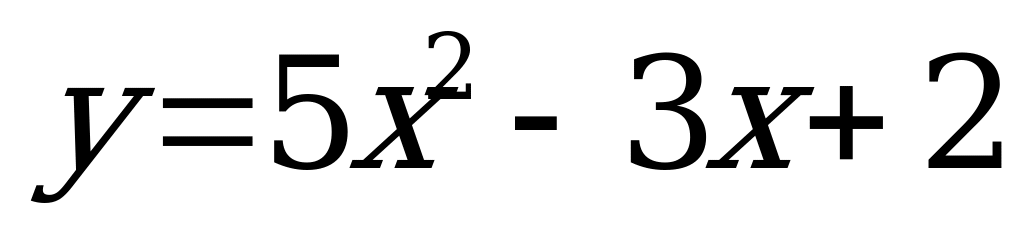 в его точке с абсциссой
в его точке с абсциссой 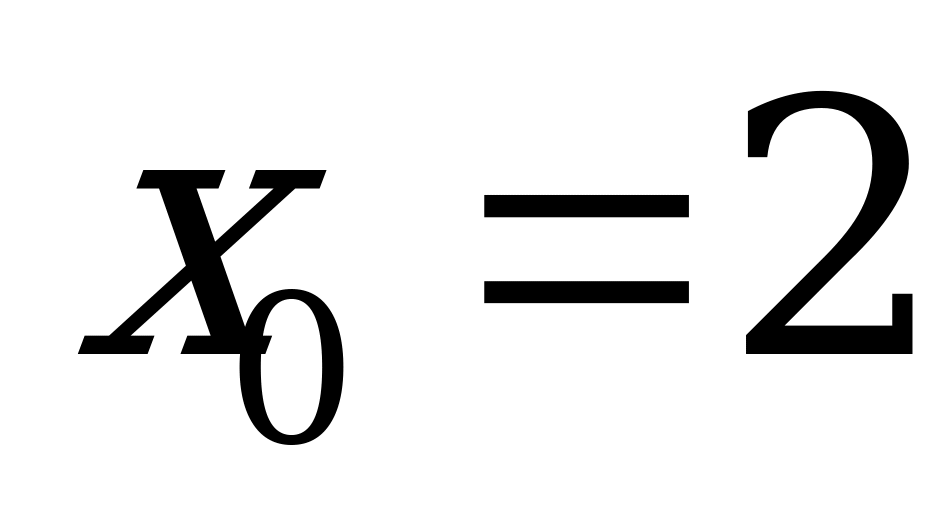 .
.
1) 16; 2) 17; 3) 0,3; 4) 0.
Часть 2.
В1. Пусть 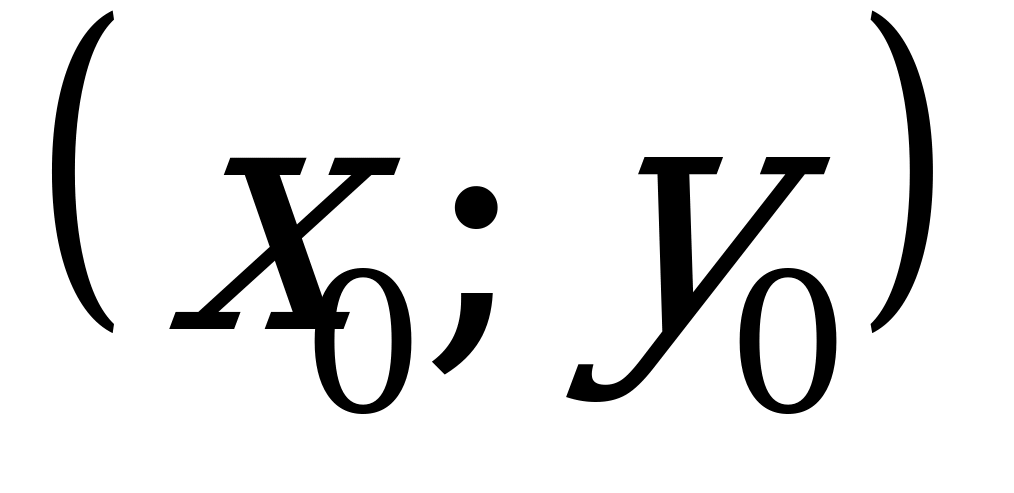 решение системы
решение системы 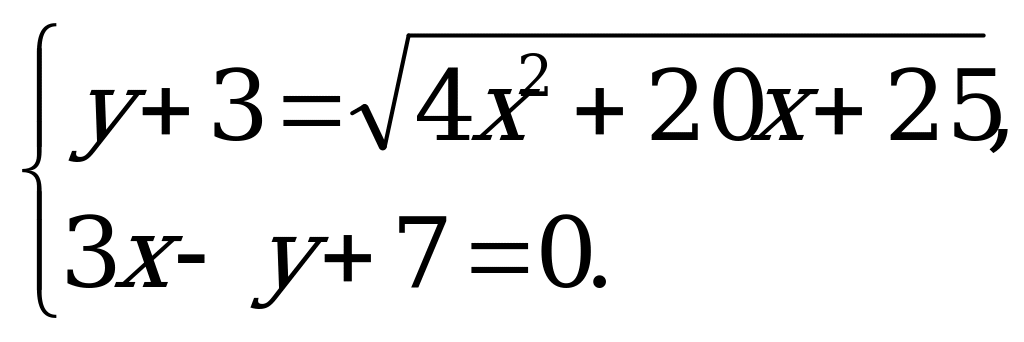 . Найдите произведение
. Найдите произведение 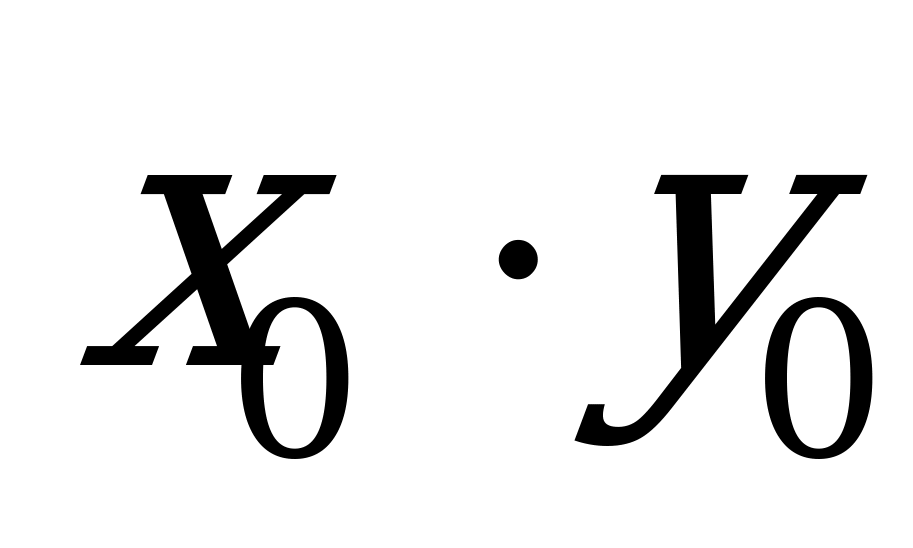 .
.
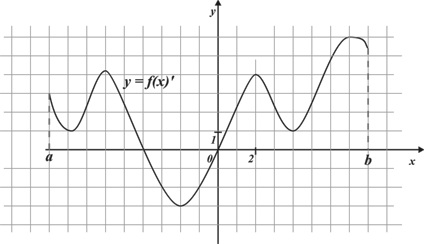
В2. На рисунке изображен график производной функции 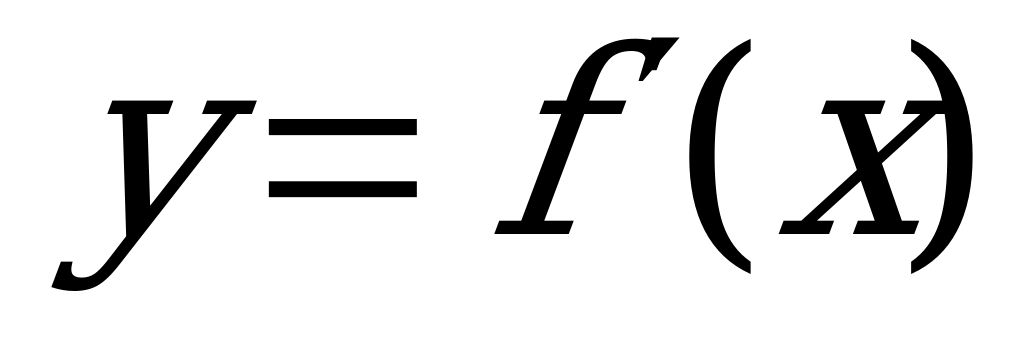 , заданной на отрезке
, заданной на отрезке 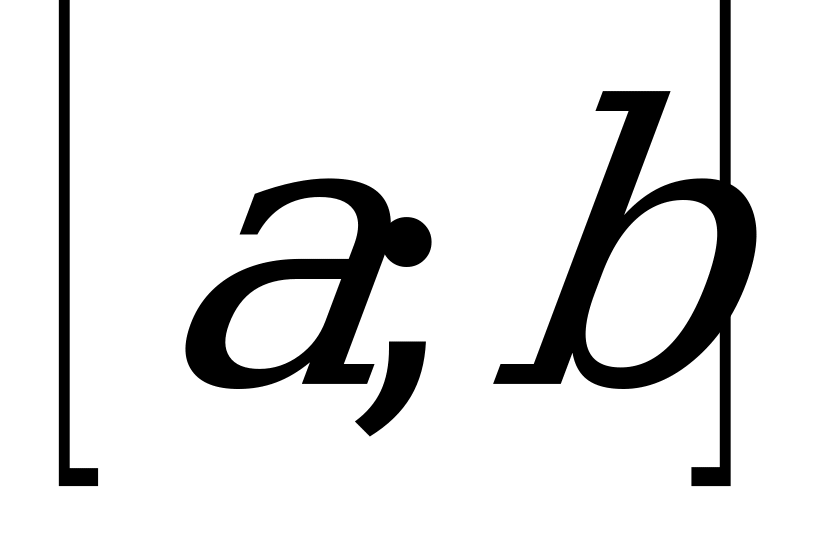 . Исследуйте функцию
. Исследуйте функцию 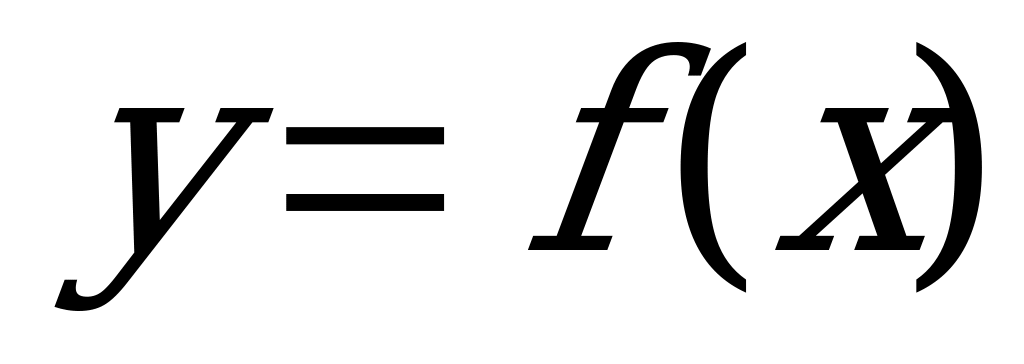 на монотонность и в ответе укажите число промежутков возрастания.
на монотонность и в ответе укажите число промежутков возрастания.
В3. Найдите значение выражения 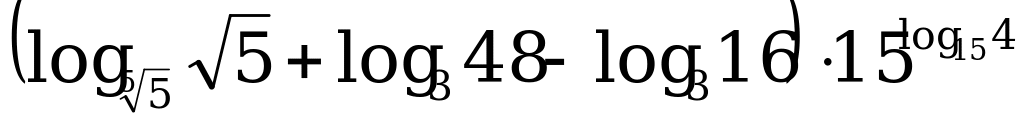 .
.
В4. Найдите наибольшее целое значение функции 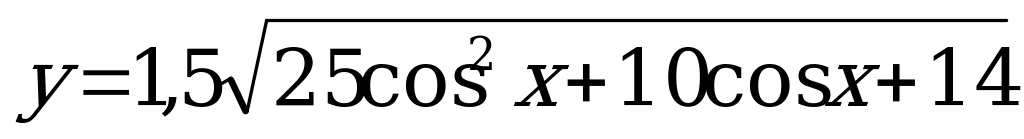 .
.
В5. Укажите число корней уравнения 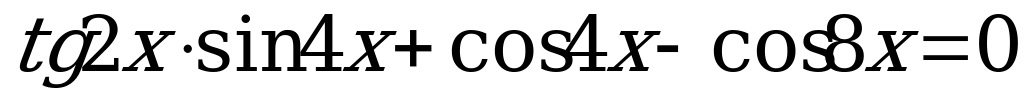 на промежутке
на промежутке 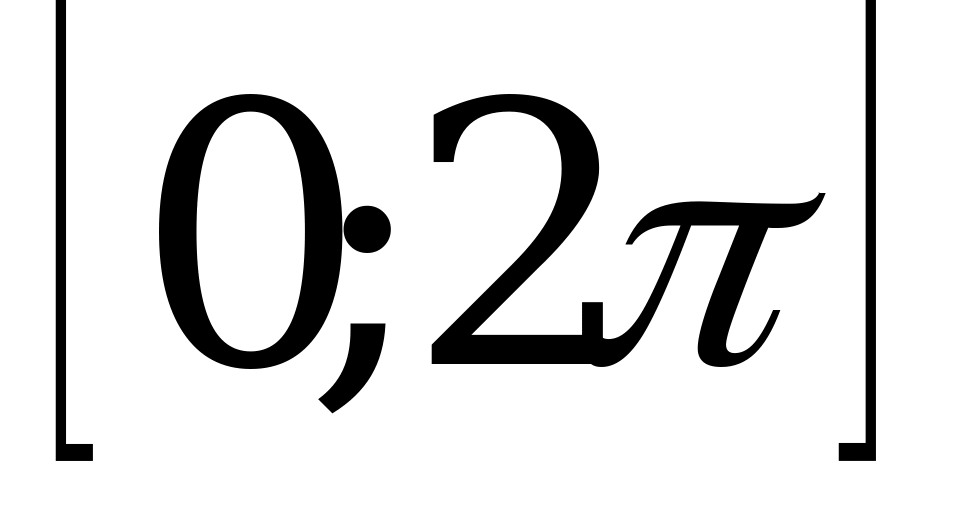 .
.
В6. При каком значении 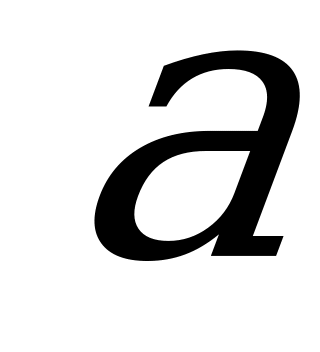 функция
функция 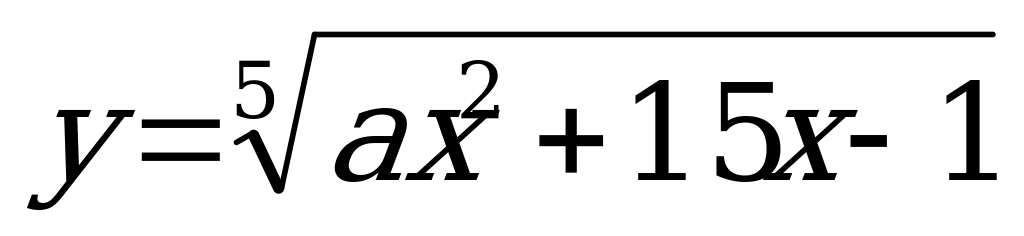 имеет максимум в точке
имеет максимум в точке 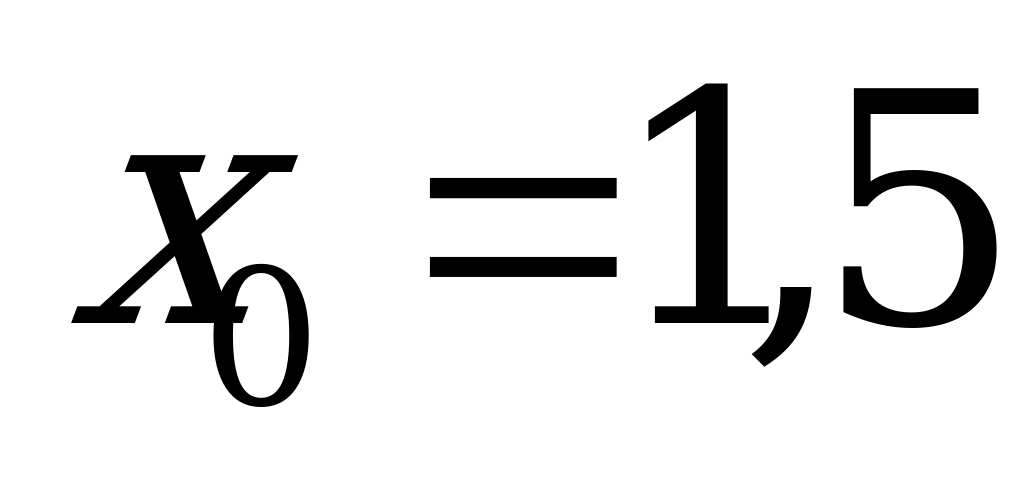 .
.
В7. К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20% той же соли. Сколько процентов соли содержится в получившемся растворе?
В8. Десятый член арифметической прогрессии равен 19, а сумма первых пятидесяти членов равна 2500. Найдите сумму третьего, двенадцатого и двадцатого членов этой прогрессии.
В9. Вычислите объем правильной треугольной пирамиды, высота которой равна 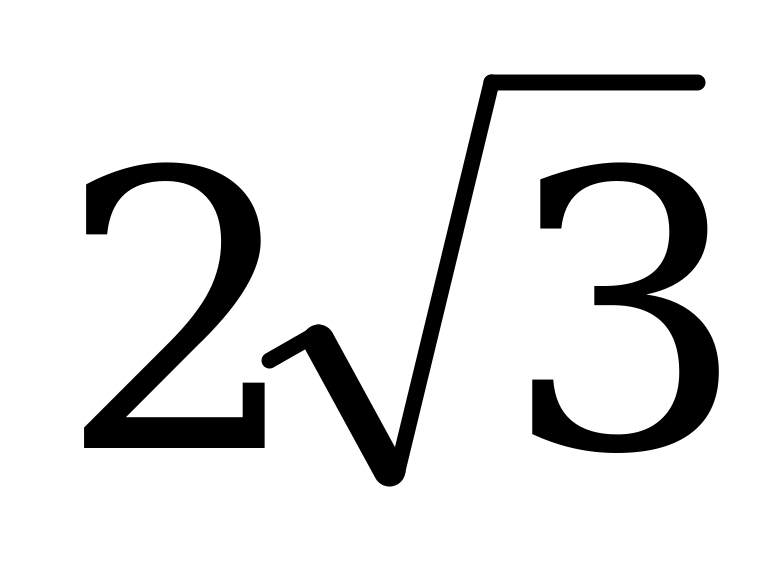 , а все плоские углы при вершине прямые.
, а все плоские углы при вершине прямые.
В10. Найдите основание равнобедренного треугольника, если угол при основании равен  , а взятая внутри треугольника точка находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии
, а взятая внутри треугольника точка находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии 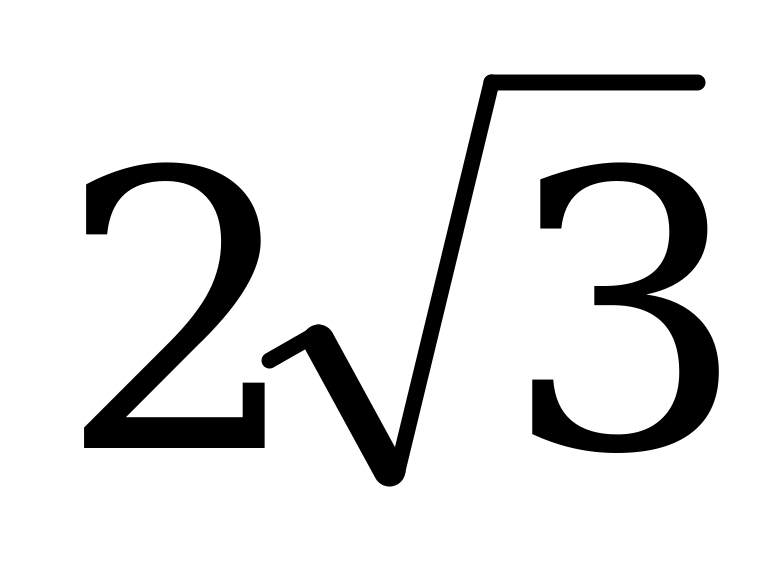 от основания.
от основания.
Часть 3.
С1. Решите уравнение 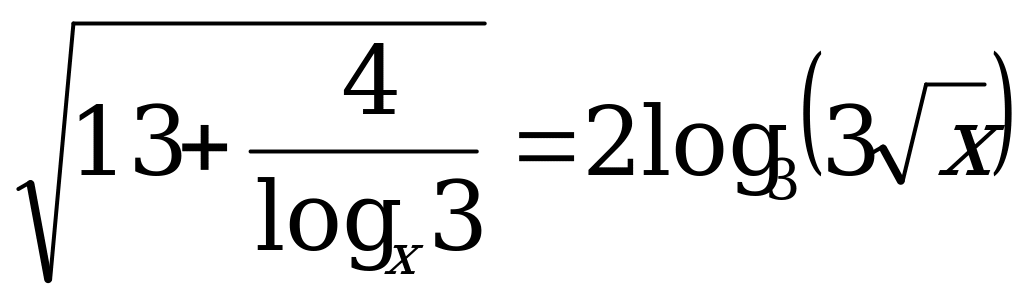 .
.
С2. Найдите все значения 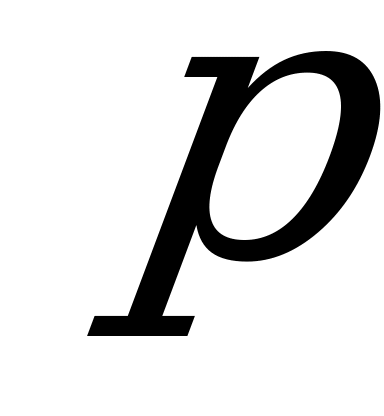 , при которых уравнение
, при которых уравнение 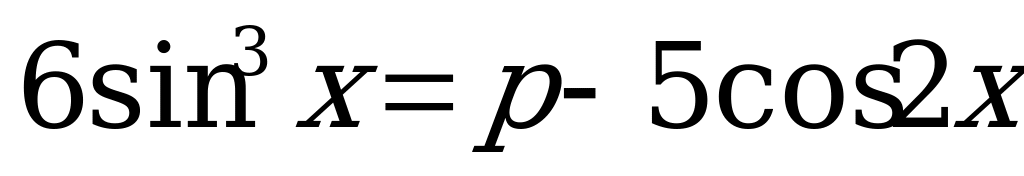 не имеет корней.
не имеет корней.
С3. Около правильной шестиугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 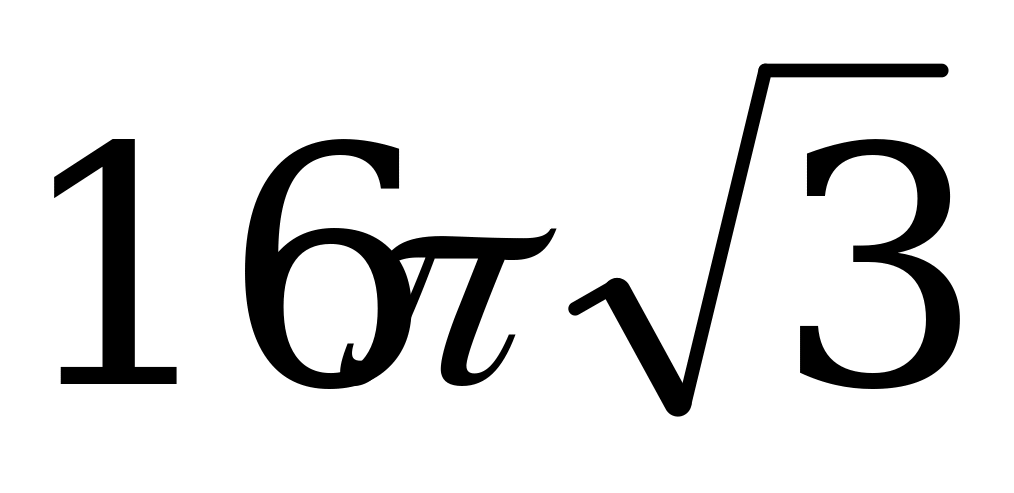 . Расстояние между осью цилиндра и диагональю боковой грани призмы равно
. Расстояние между осью цилиндра и диагональю боковой грани призмы равно 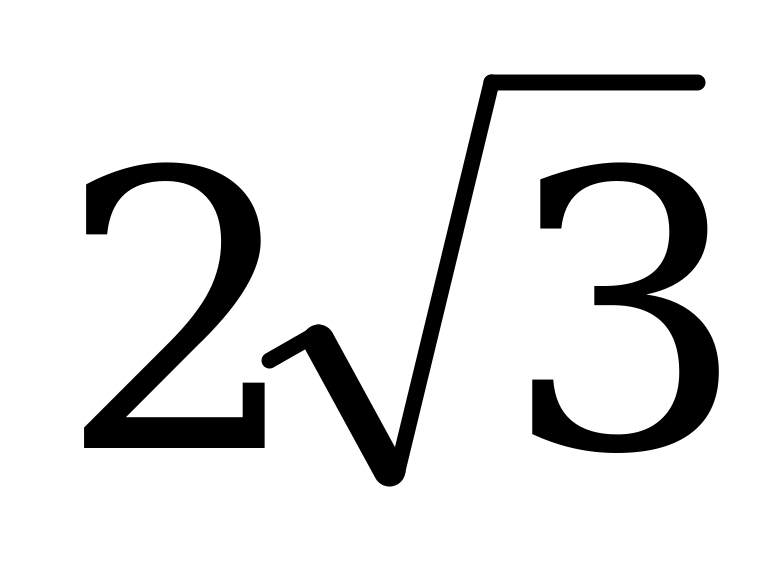 . Найдите объем призмы.
. Найдите объем призмы.
С4. Найдите все значения параметра 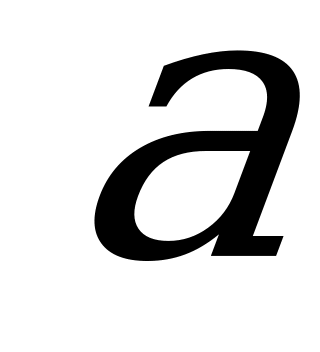 , при которых область определения функции
, при которых область определения функции 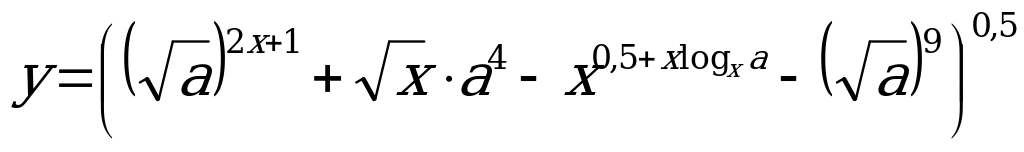 содержит два или три целых числа.
содержит два или три целых числа.
Ответы к варианту ЕГЭ. (2003 г)
Ответы к заданиям части А.
| Задание | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| № ответа | 3 | 4 | 1 | 3 | 3 | 1 | 4 | 3 |
| Задание | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| № ответа | 2 | 4 | 1 | 1 | 3 | 1 | 2 | 2 |
Ответы к заданиям части В.
| Задание | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | 6 | 2 | 13 | 10 | 5 | -5 | 32 | 67 | 36 | 24 |
Ответы к заданиям части С.
| Задание | 1 | 2 | 3 | 4 |
| Ответ | 27 | 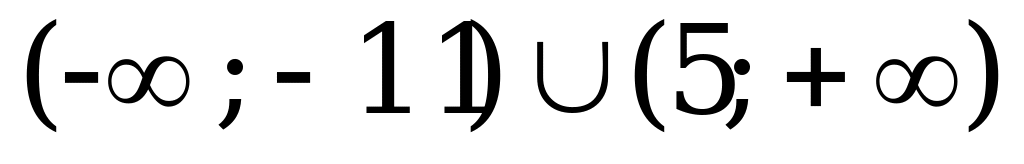
| 144 | 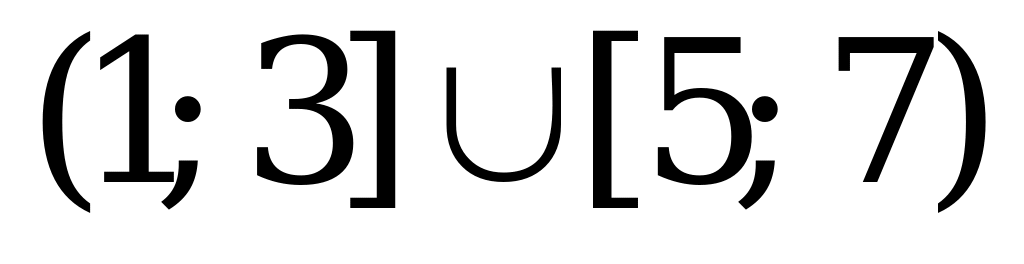
|
3. Итоги урока.
4. Домашнее задание.
Задания из ЕГЭ.
Урок 102.
Заключительный.
На этом уроке проводится анализ решения ЕГЭ, и подводятся итоги.
ТРЕНИРОВАЧНЫЙ ВАРИАНТ ЕГЭ. (2004 год.)
Часть 1.
А1. Вычислить 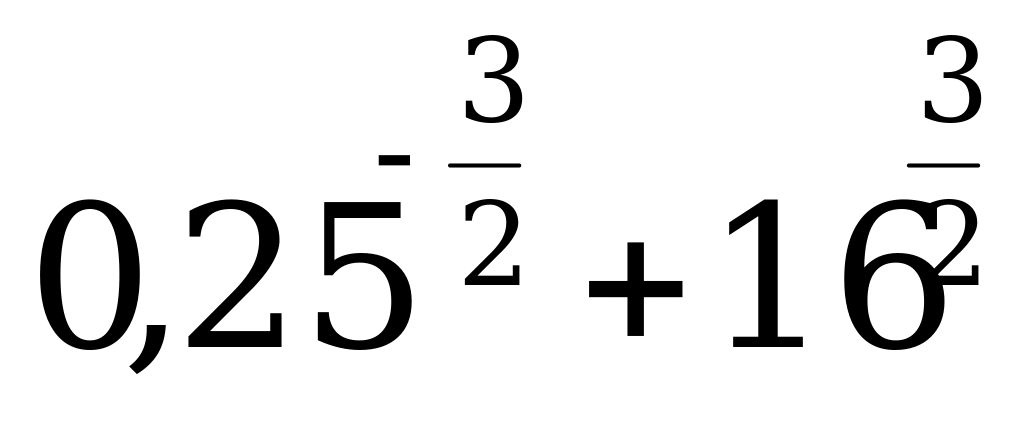 .
.
1) 1; 2) – 148,5; 3) 133; 4) 125,5.
А2. Упростите выражения 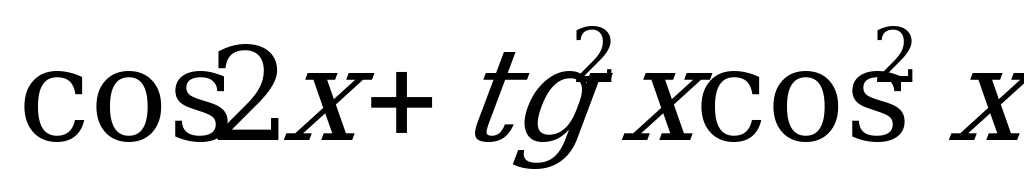 .
.
1)  ; 2)
; 2) 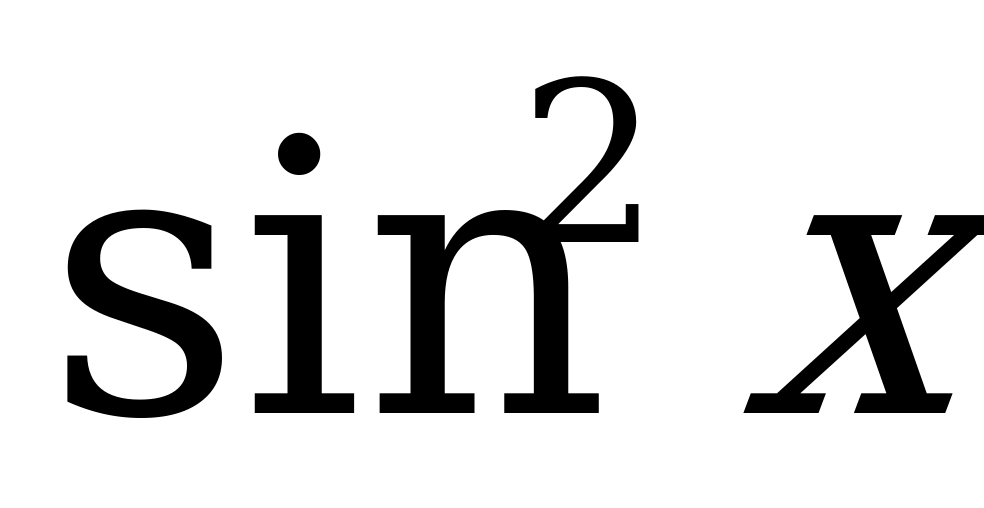 ; 3)
; 3) 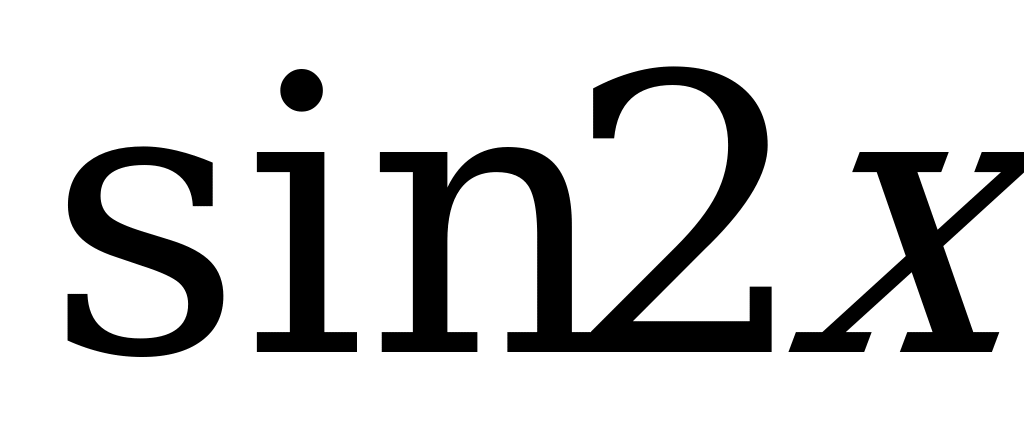 ; 4)
; 4) 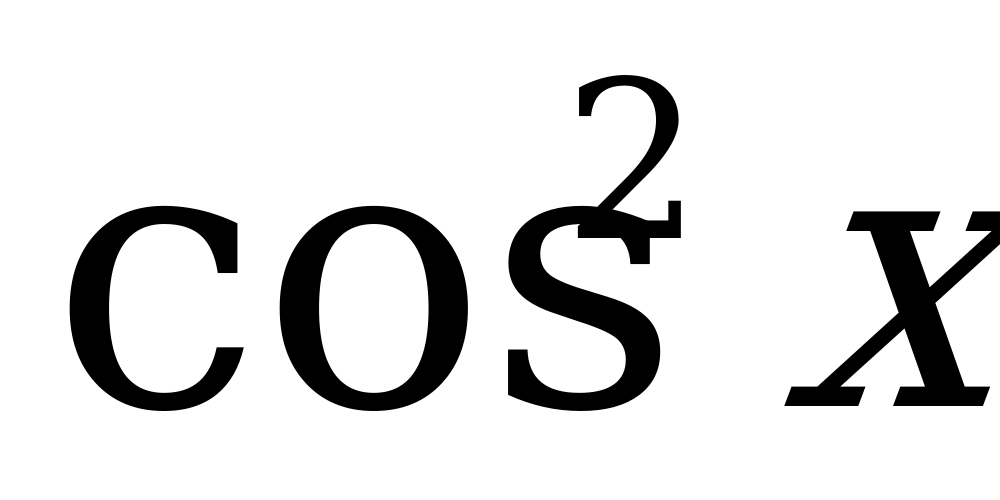 .
.
А3. Упростите выражения 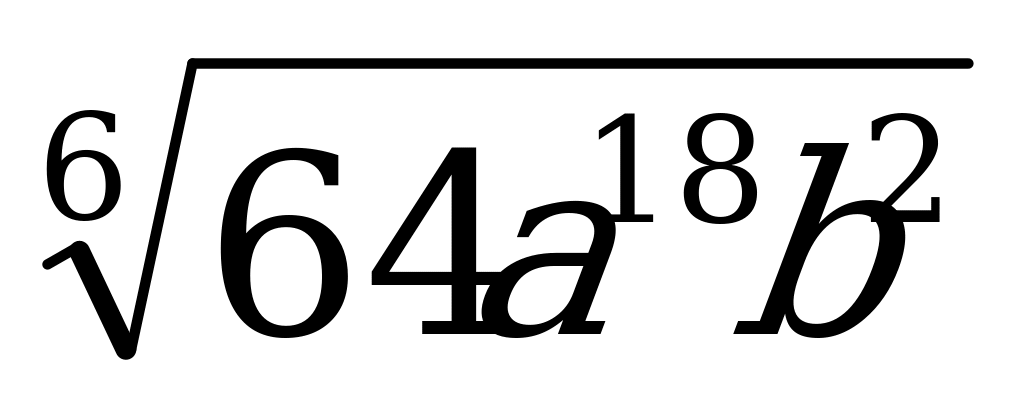 , если
, если 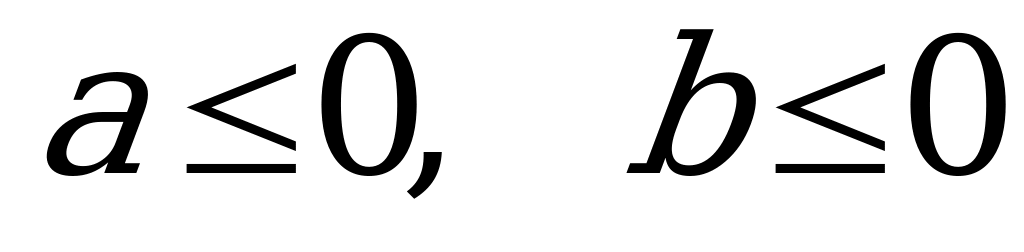 .
.
1) 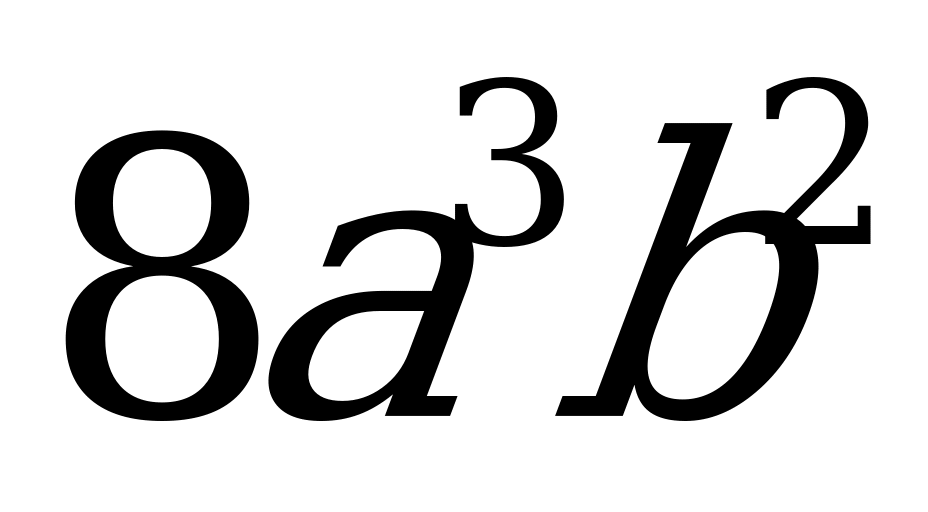 ; 2)
; 2) 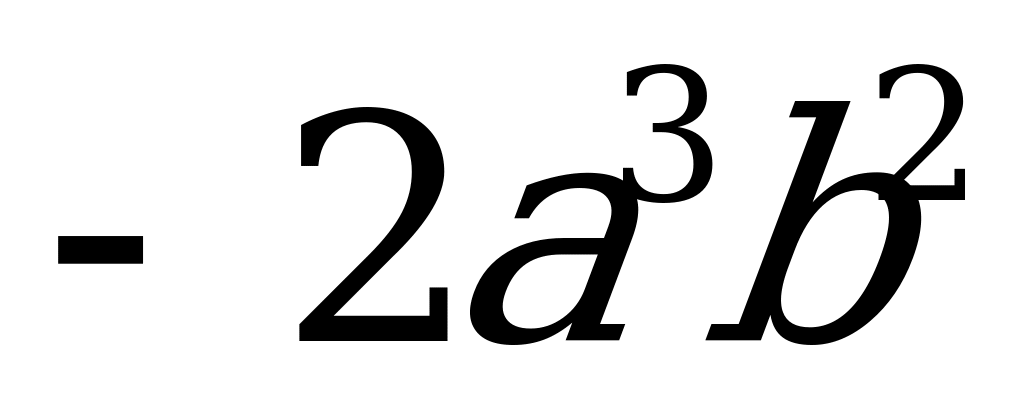 ; 3)
; 3) 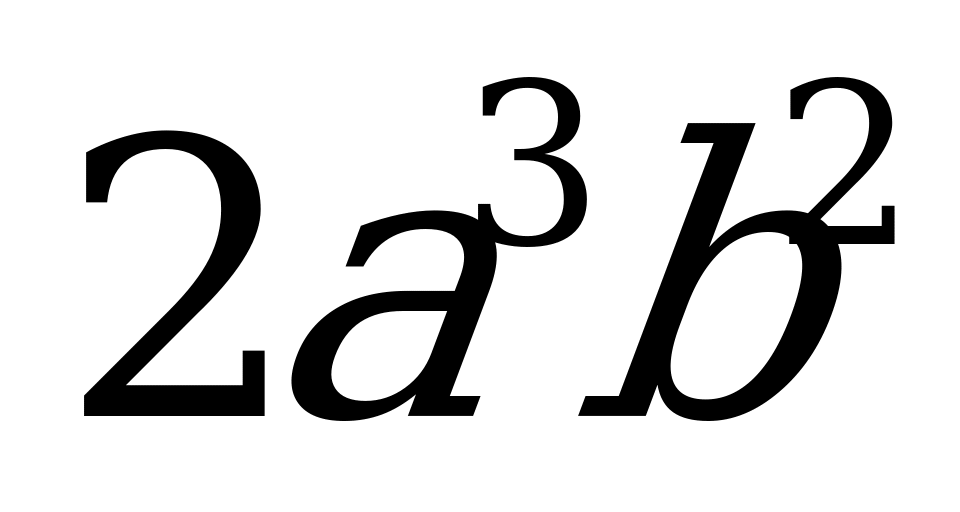 ; 4)
; 4) 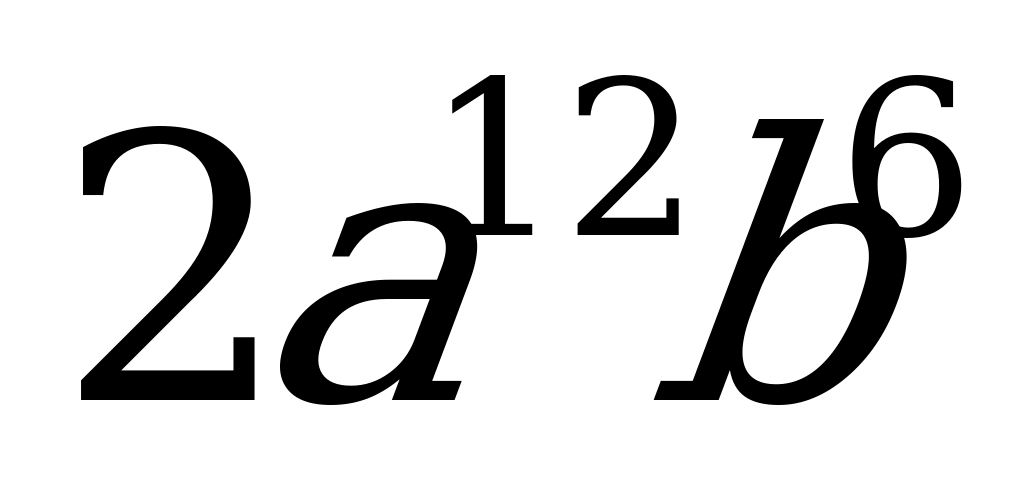 .
.
А4. Найдите значение 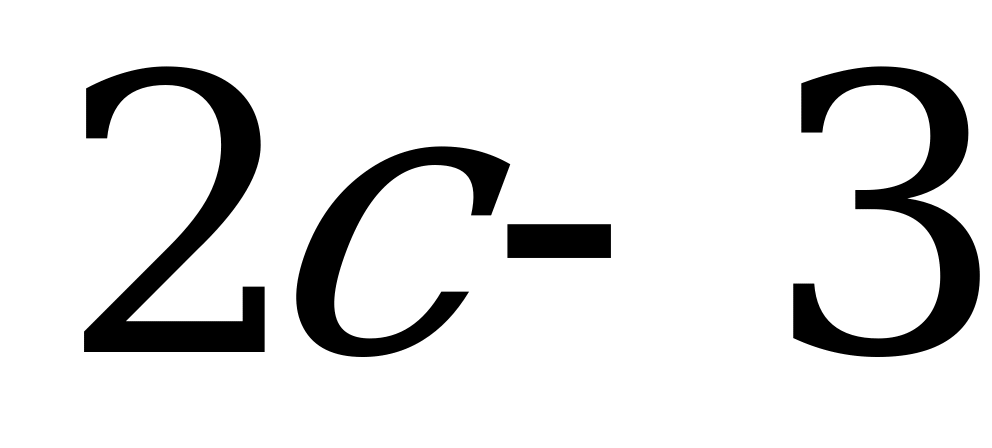 , если
, если 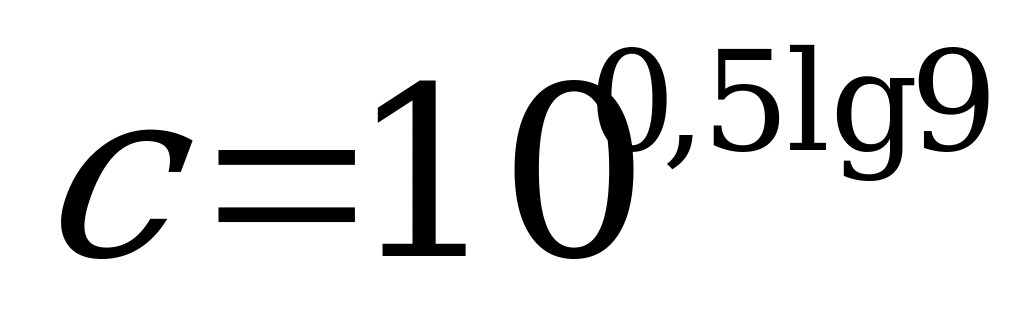 .
.
1) – 1; 2) 15; 3) 3; 4) 6.
А5. Укажите промежуток, которому принадлежит корень уравнения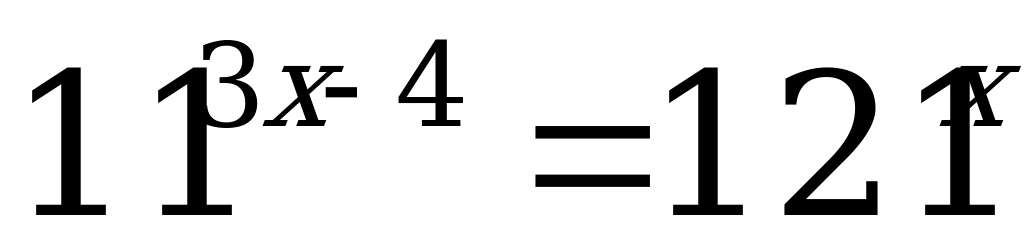 .
.
1) 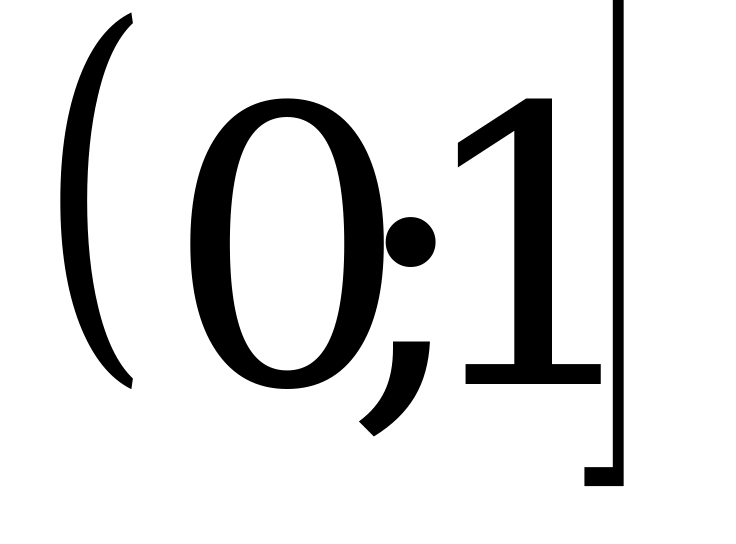 ; 2)
; 2) 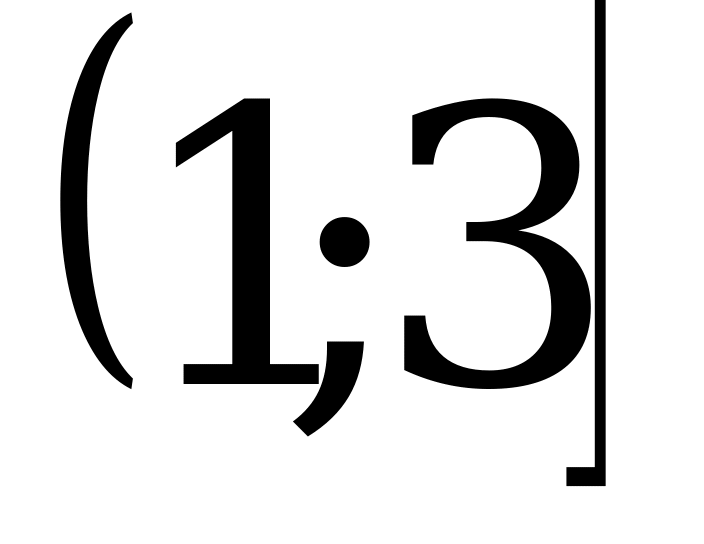 ; 3)
; 3) 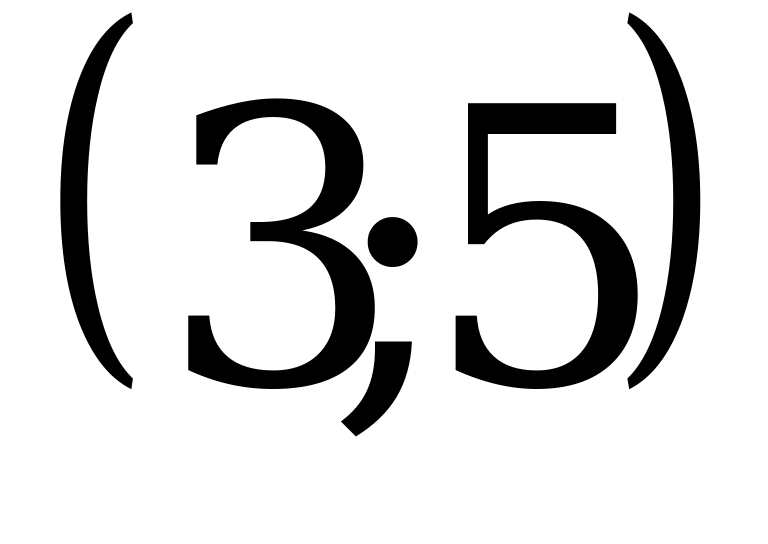 ; 4)
; 4) 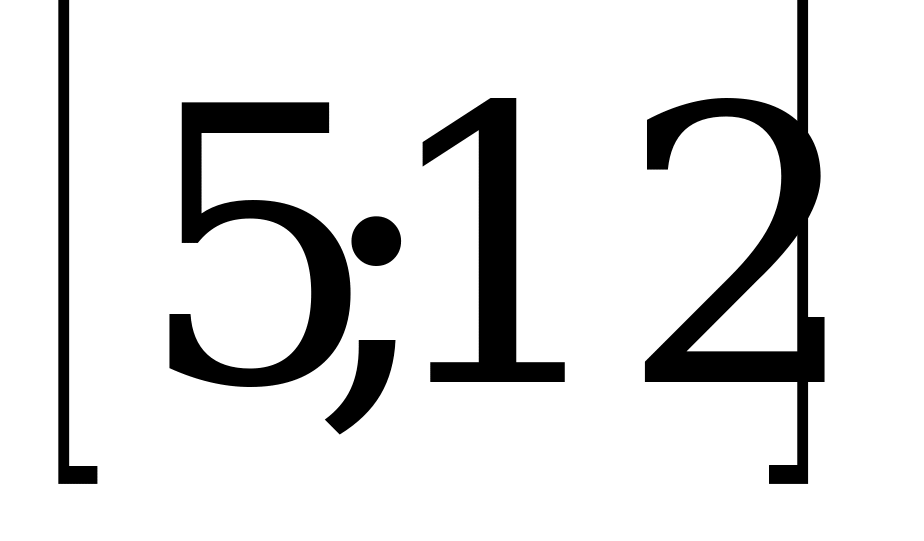 .
.
А6. Укажите промежуток, содержащий корень уравнения 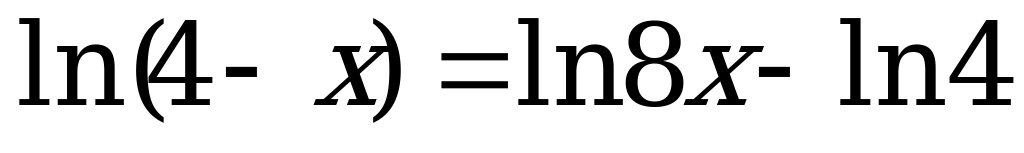 .
.
1) 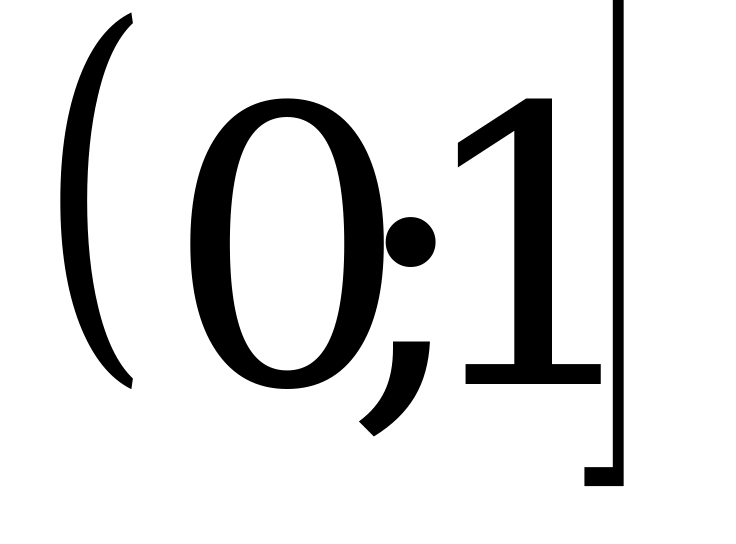 ; 2)
; 2) 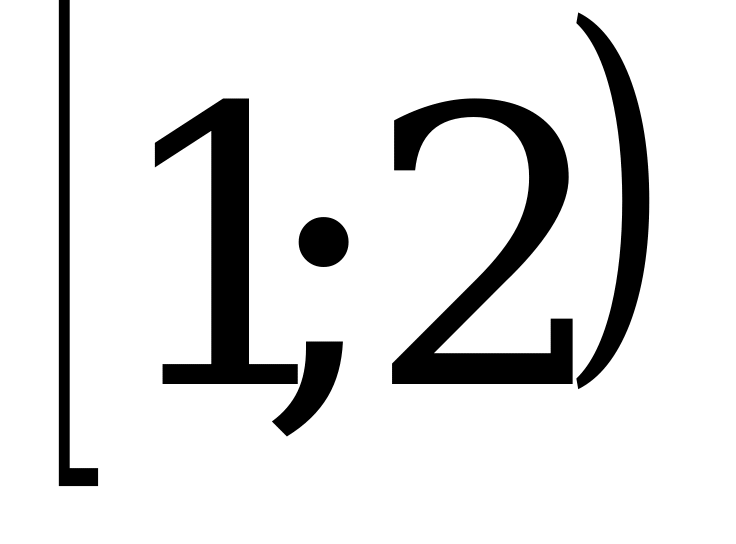 ; 3)
; 3) 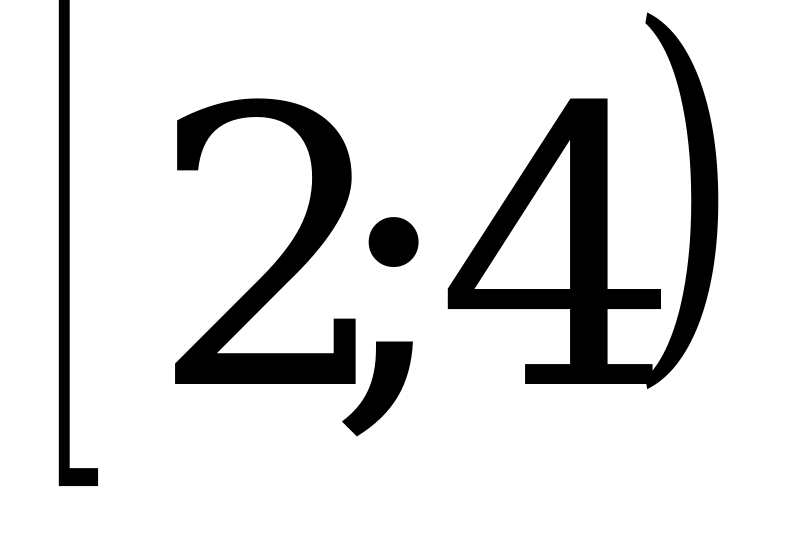 ; 4)
; 4) 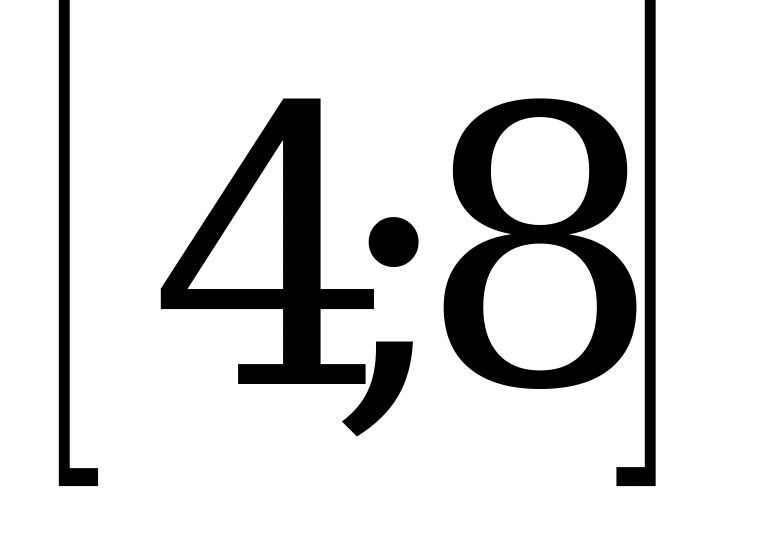 .
.
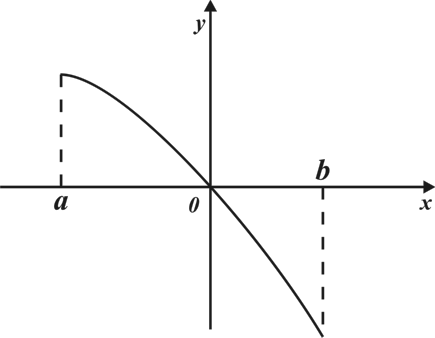
А7. На рисунке изображены графики функций, заданных на отрезке 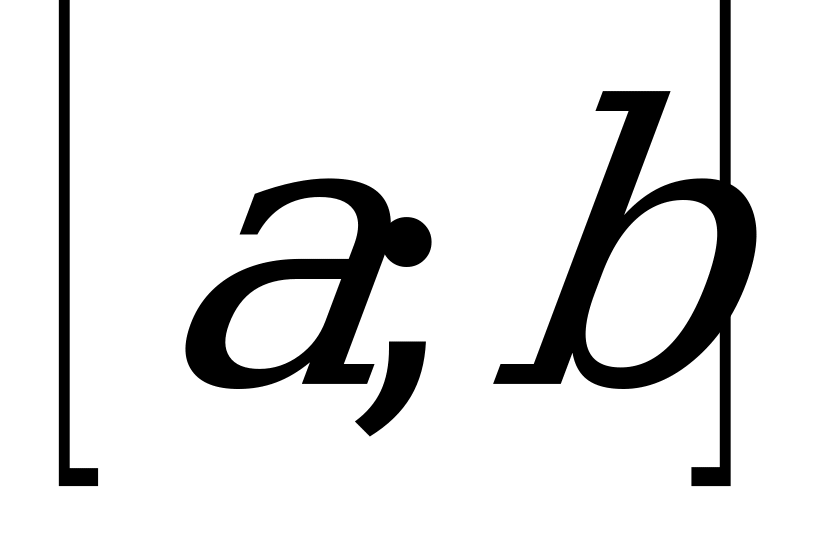 . Укажите график нечетной функции.
. Укажите график нечетной функции.
А8. Укажите множество решений неравенства 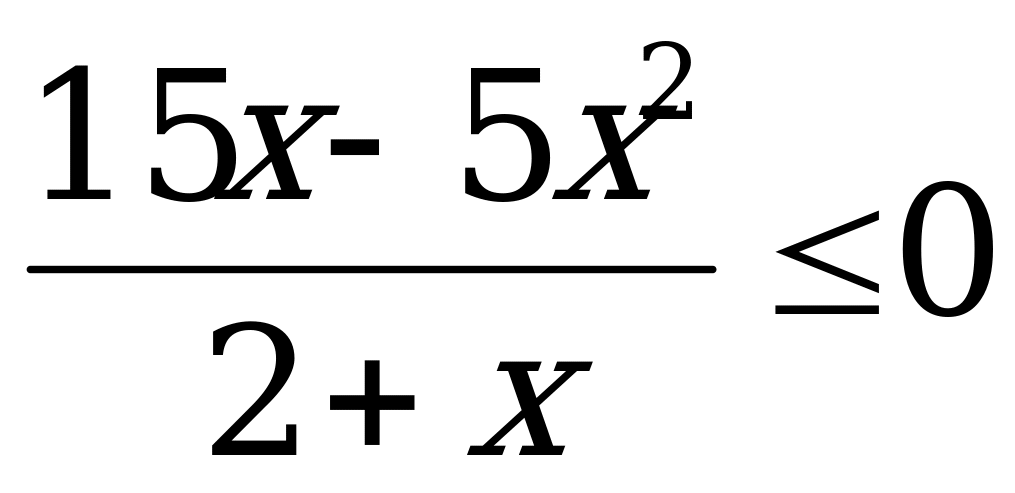 .
.
1) 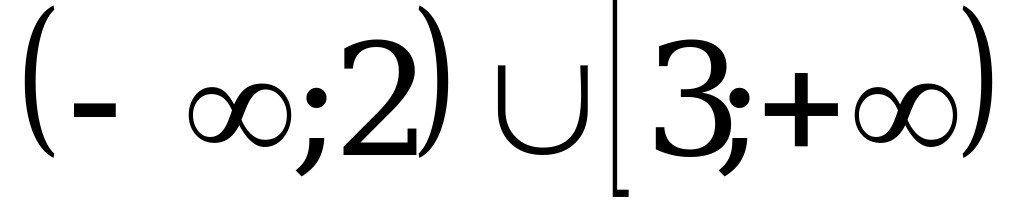 ; 2)
; 2) 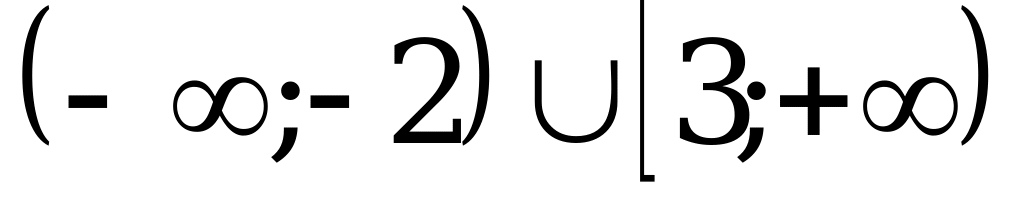 ;
;
3) 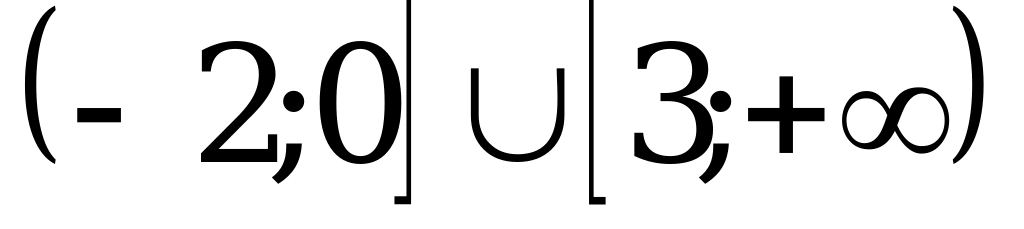 ; 4)
; 4)  .
.
А9. Вычислите значение производной функции 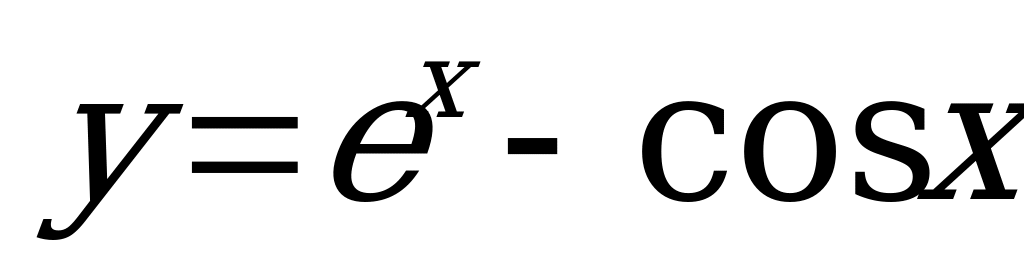 в точке
в точке 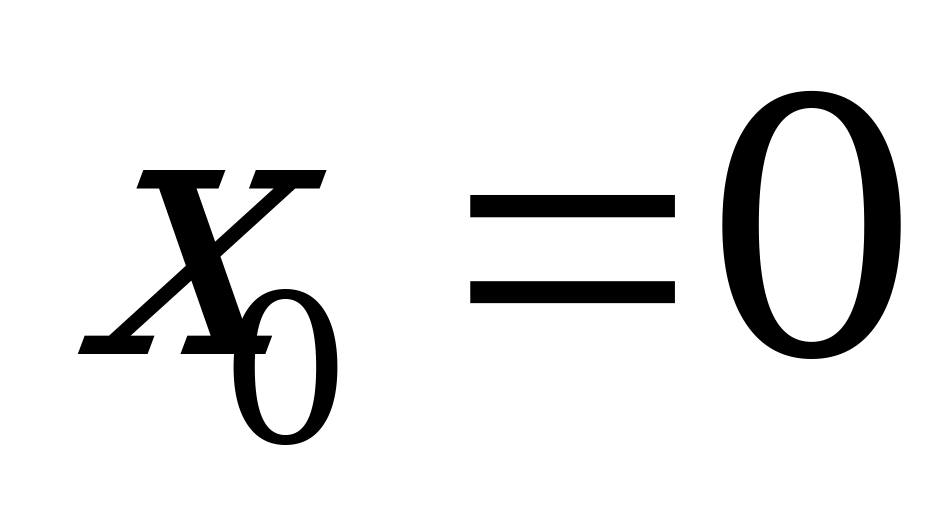 .
.
1) 1; 2) 2; 3) 0; 4) – 1.
А10. Найдите область определения функции 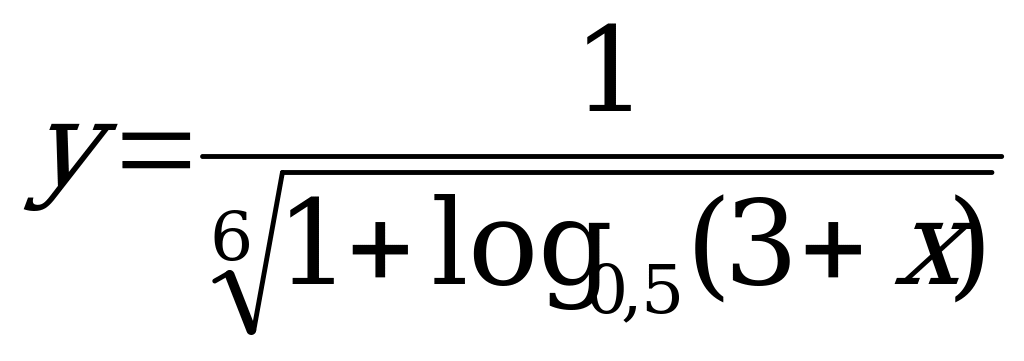 .
.
1) 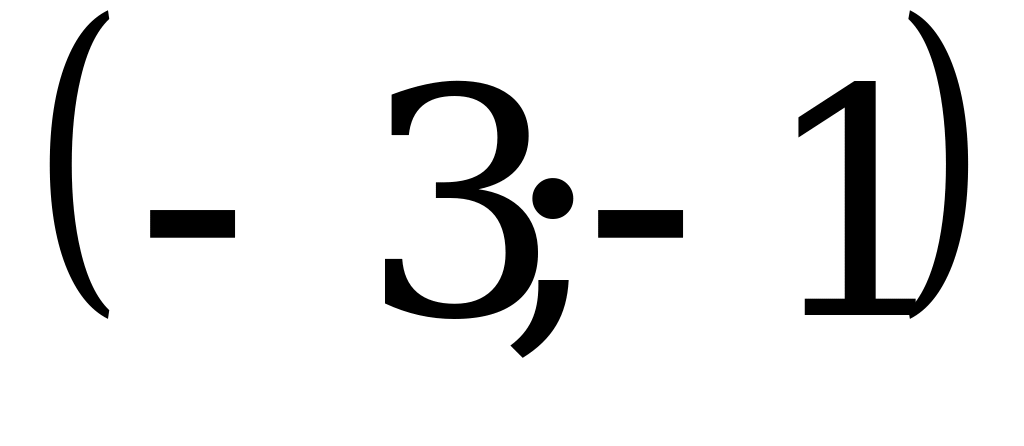 ; 2)
; 2) 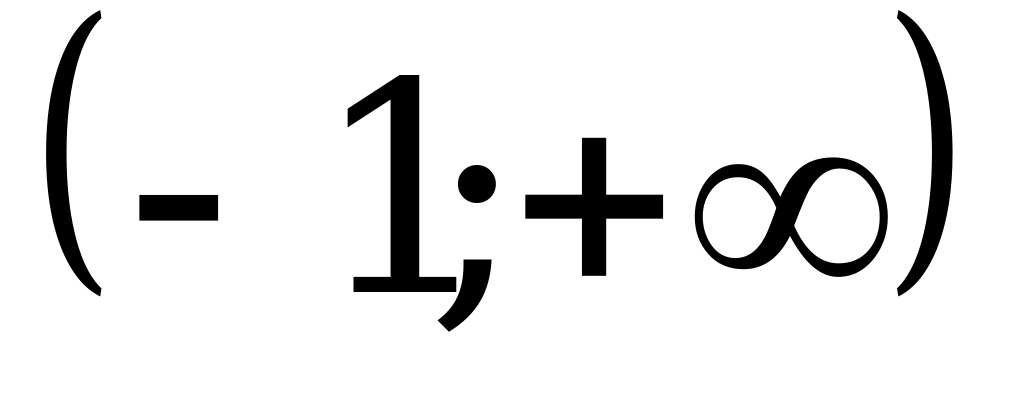 ; 3)
; 3) 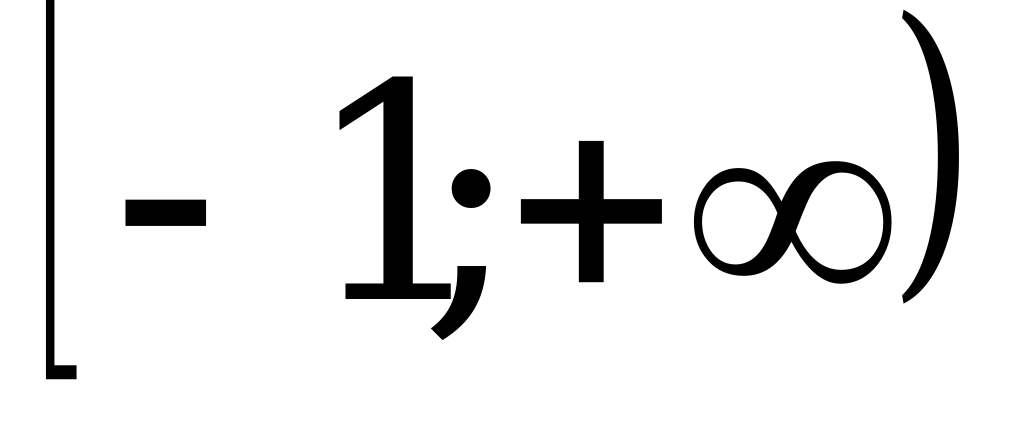 ; 4)
; 4) 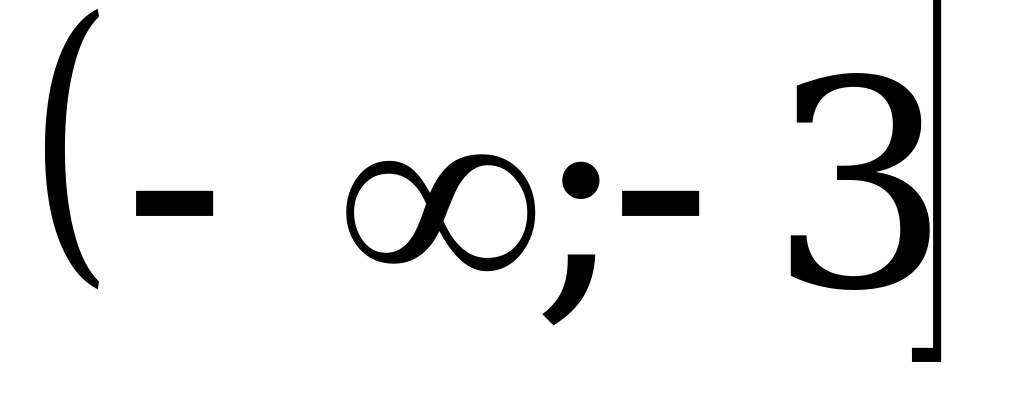 .
.
А11. Найдите множество значений функции 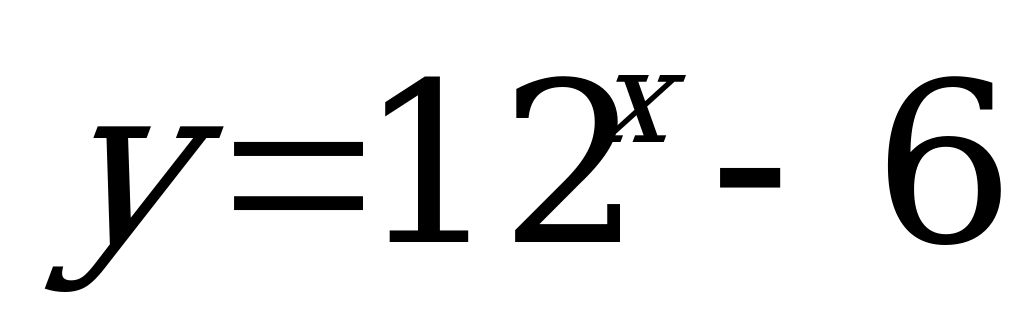 .
.
1) 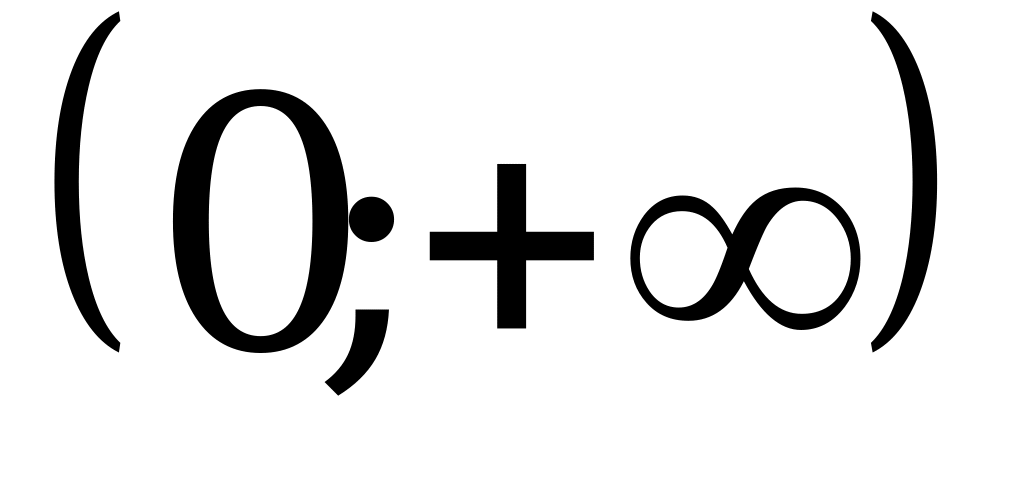 ; 2)
; 2) 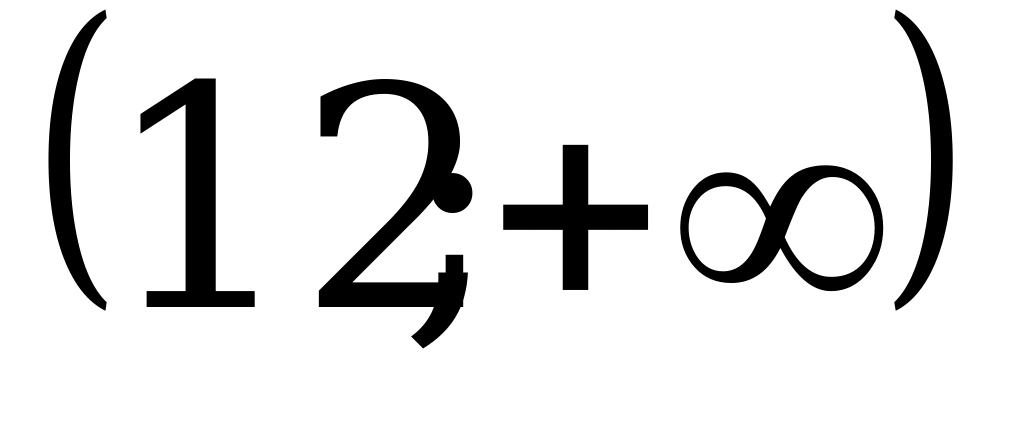 ; 3)
; 3) 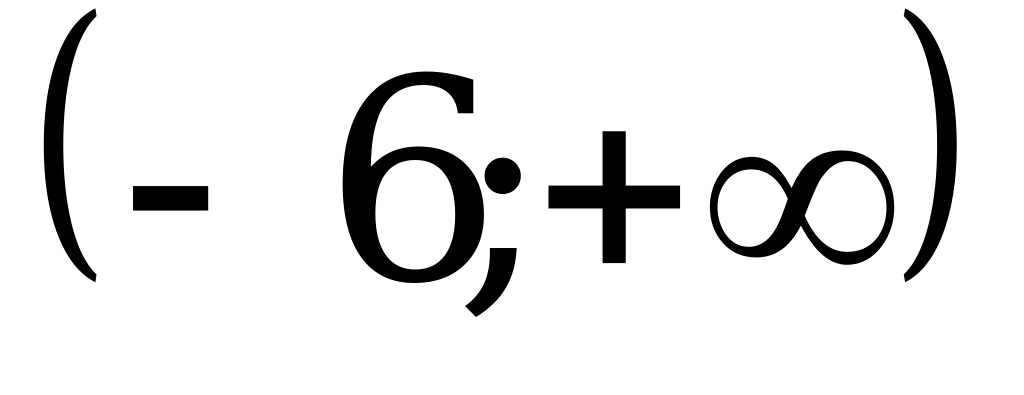 ; 4)
; 4) 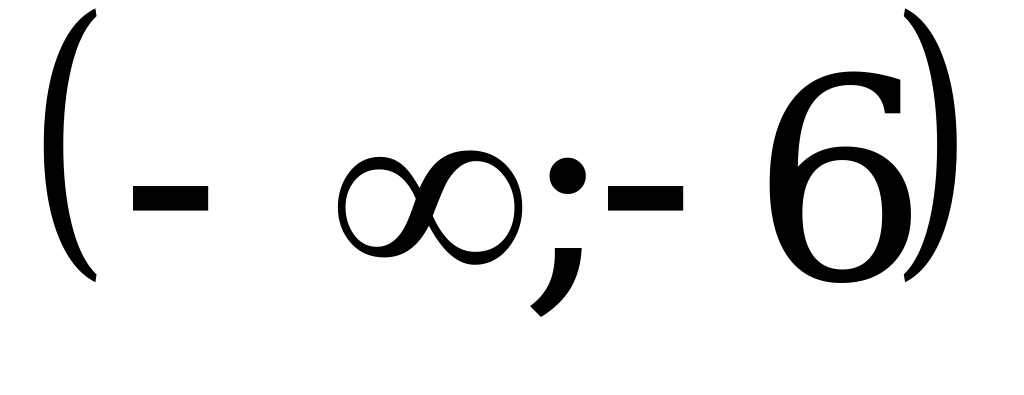 .
.
А12. Решите уравнение 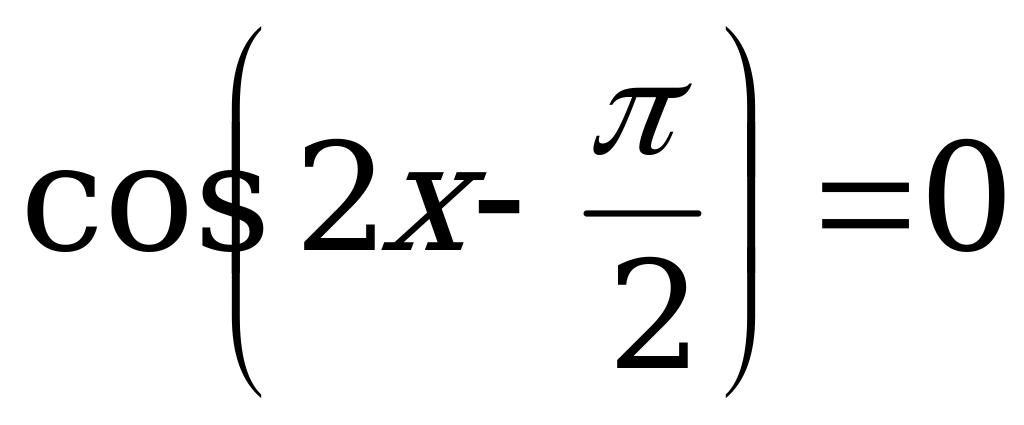 .
.
1) 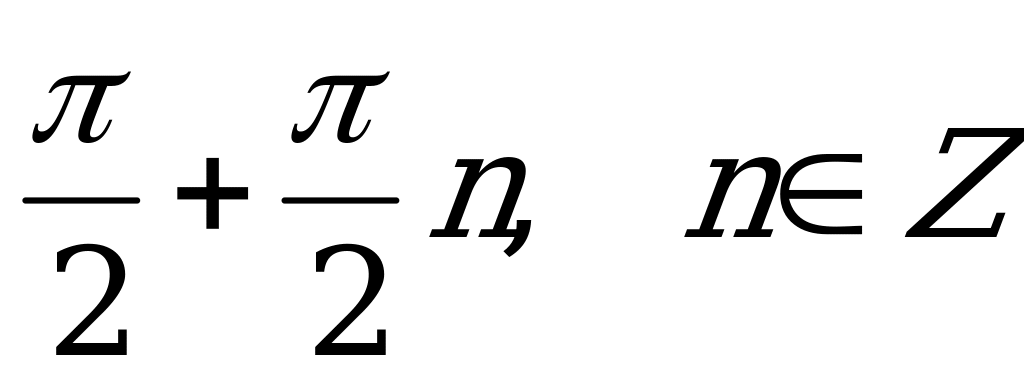 ; 2)
; 2) 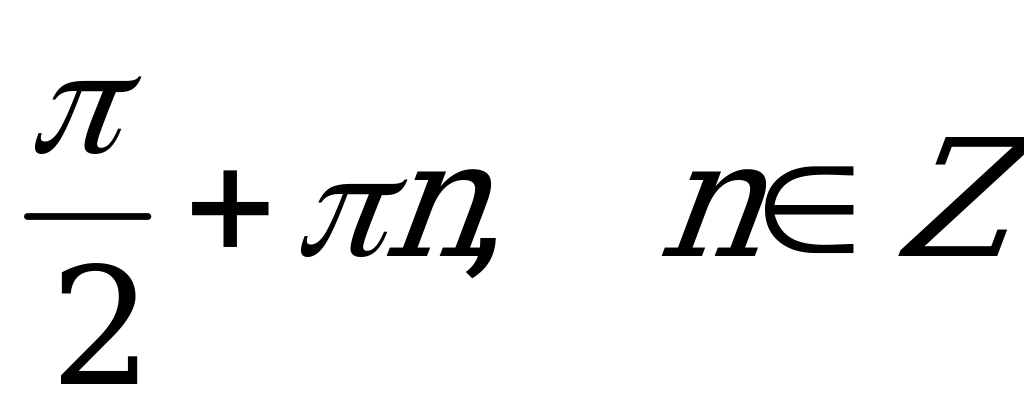 ;
;
3) 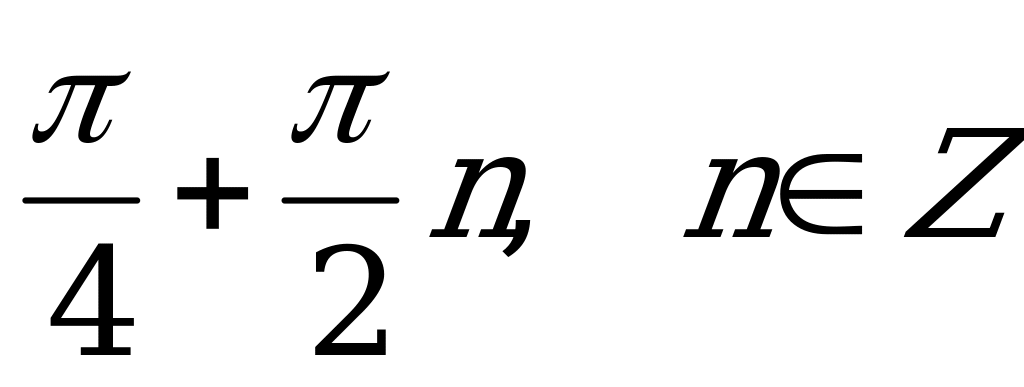 ; 4)
; 4) 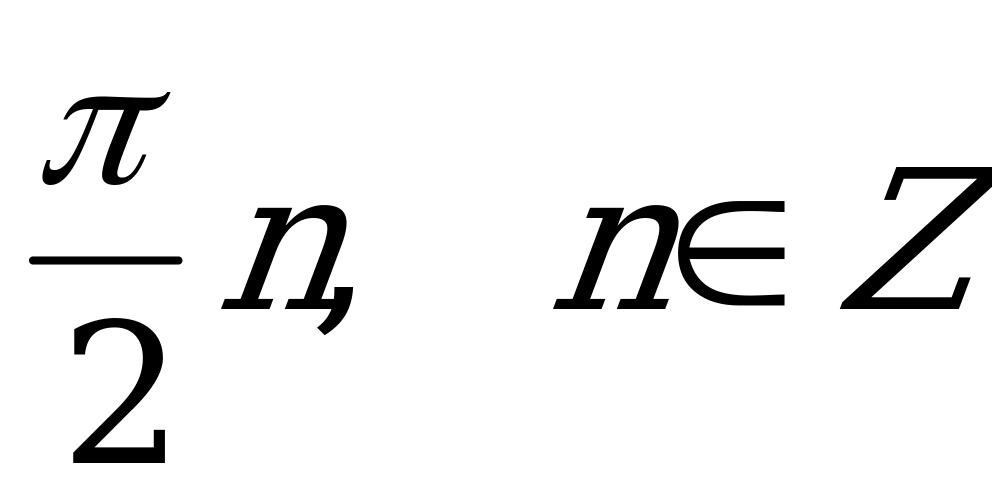 .
.
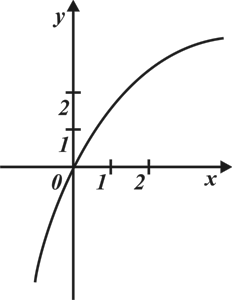
А13. На рисунке изображен график функции 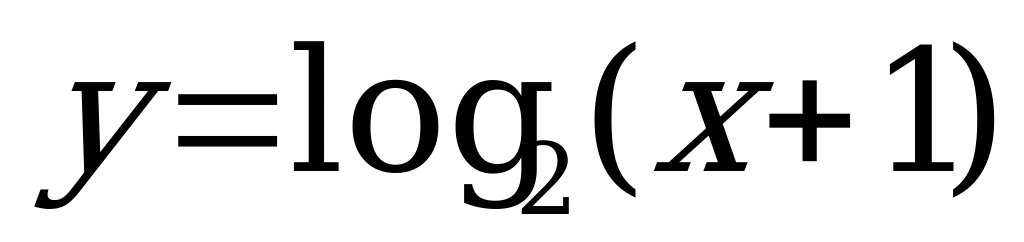 . Укажите промежуток, которому принадлежит корень уравнения
. Укажите промежуток, которому принадлежит корень уравнения 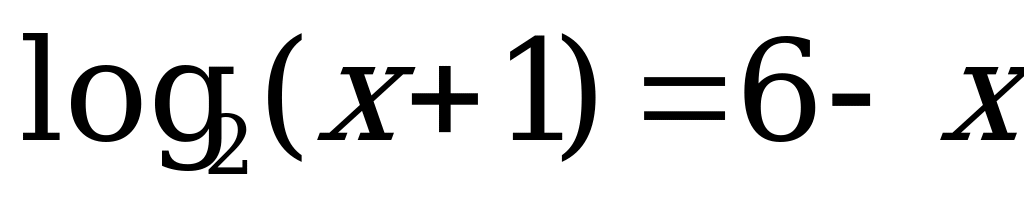 .
.
1) 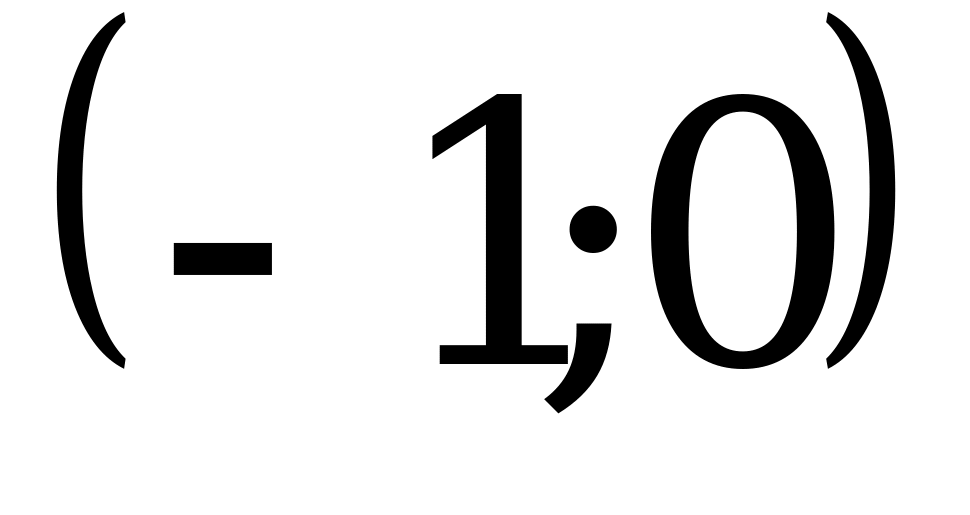 ;
;
2) 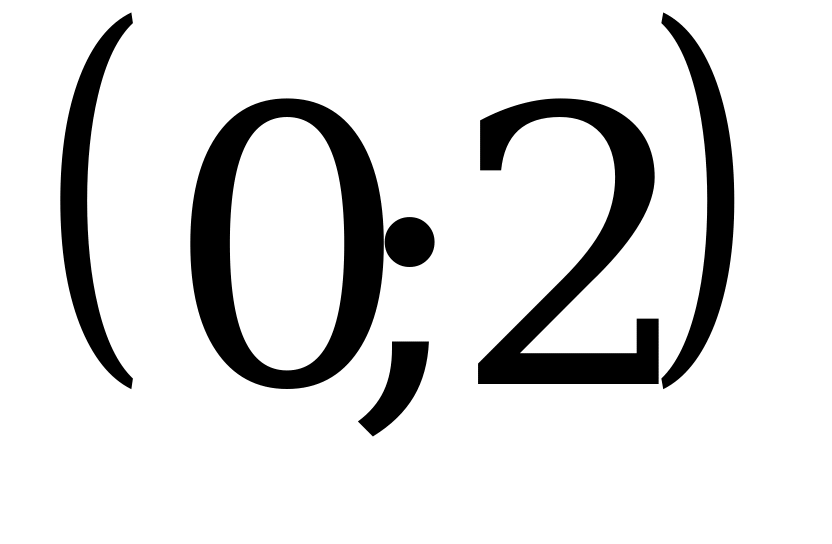 ;
;
3) 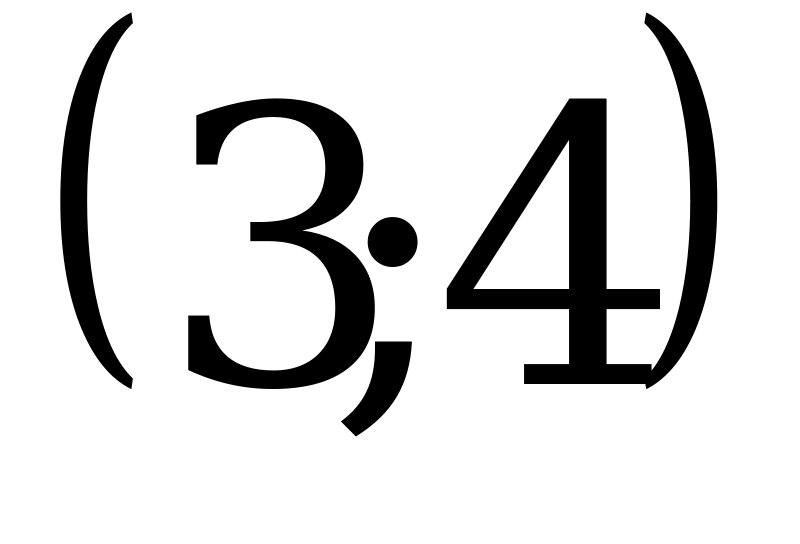 ;
;
4) 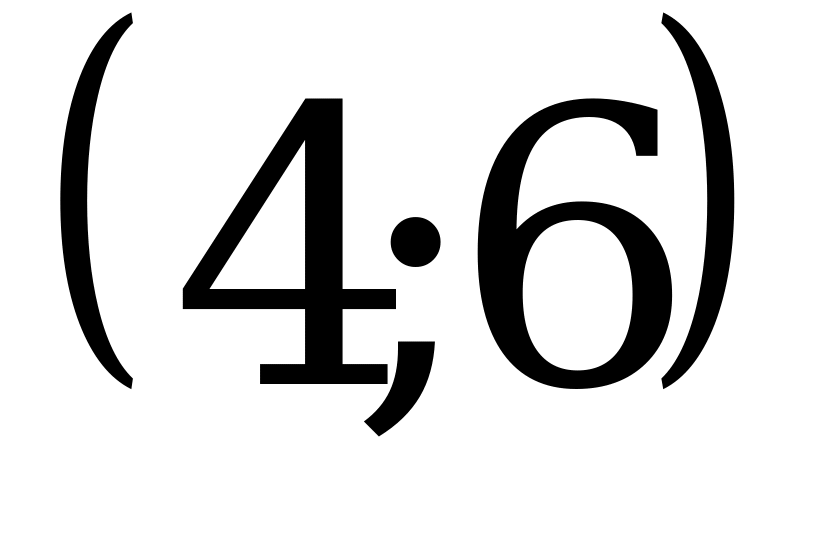 .
.
А1. Через точку графика функции 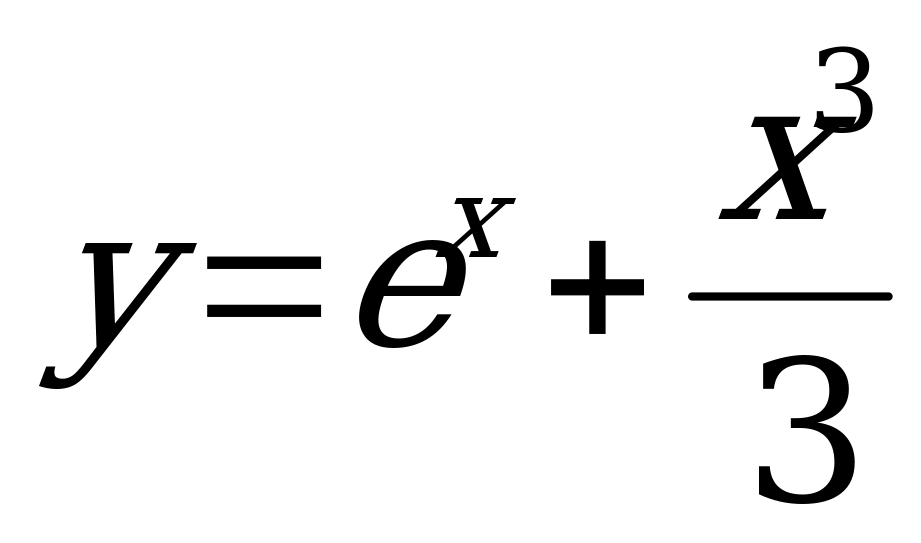 с абсциссой
с абсциссой 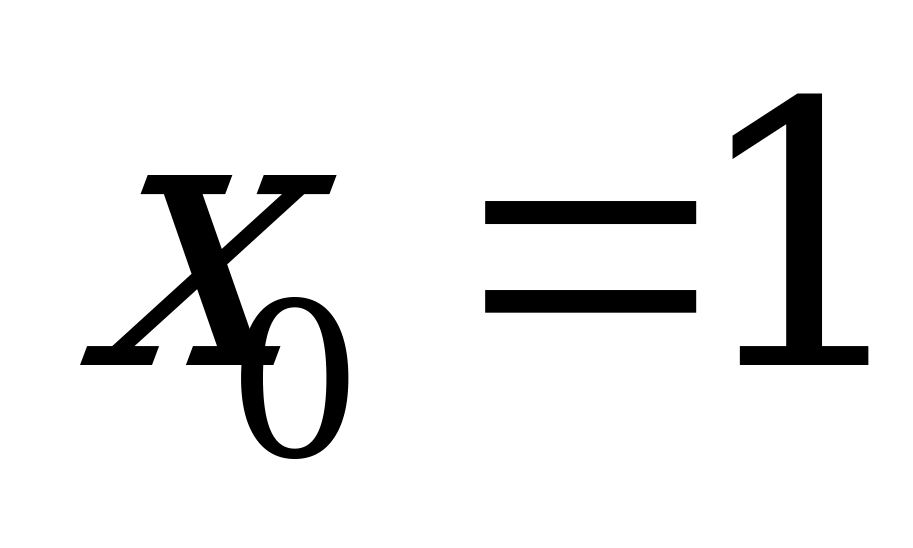 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.
проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.
1) 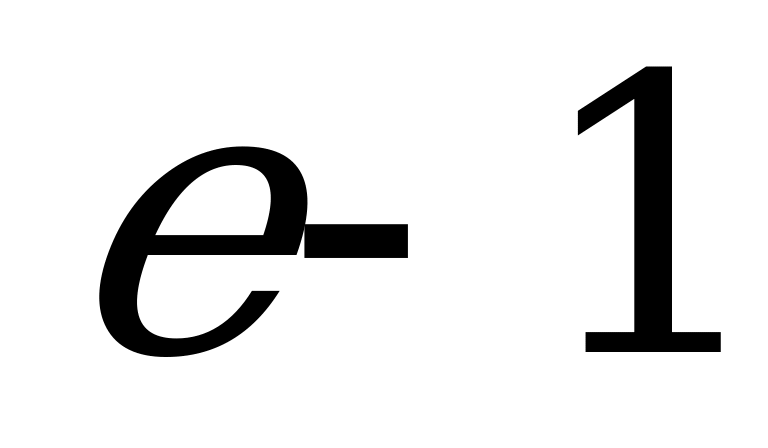 ; 2)
; 2) 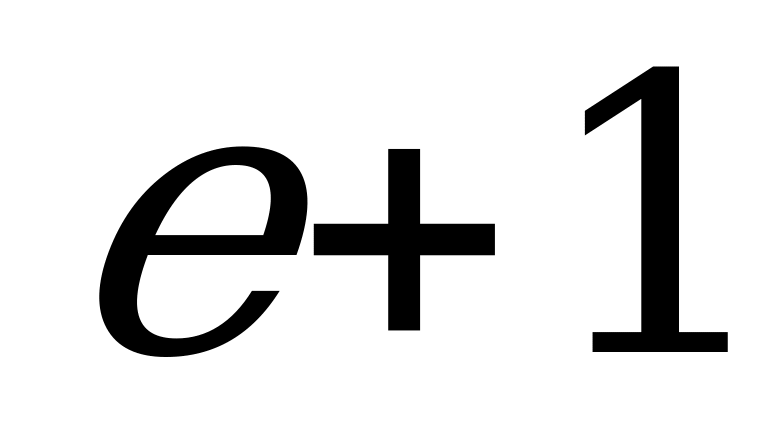 ; 3)
; 3) 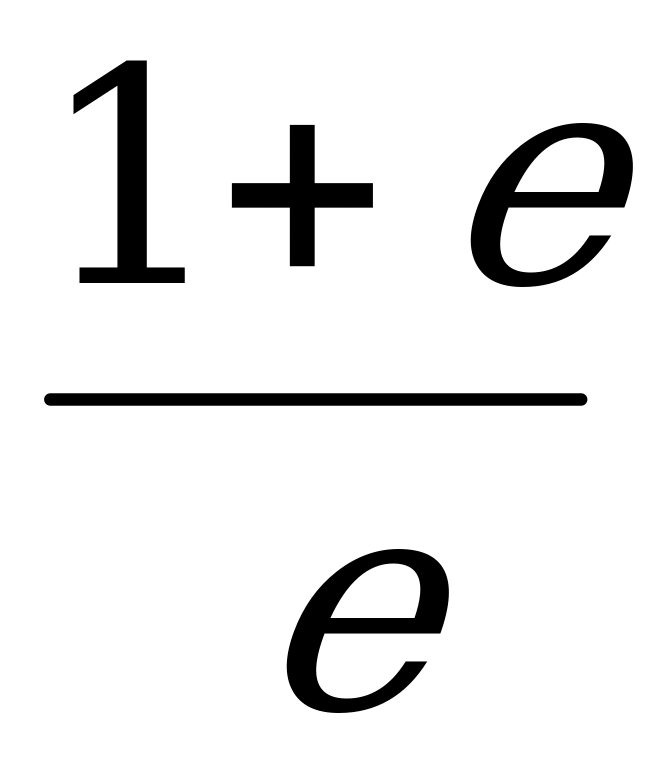 ; 4)
; 4) 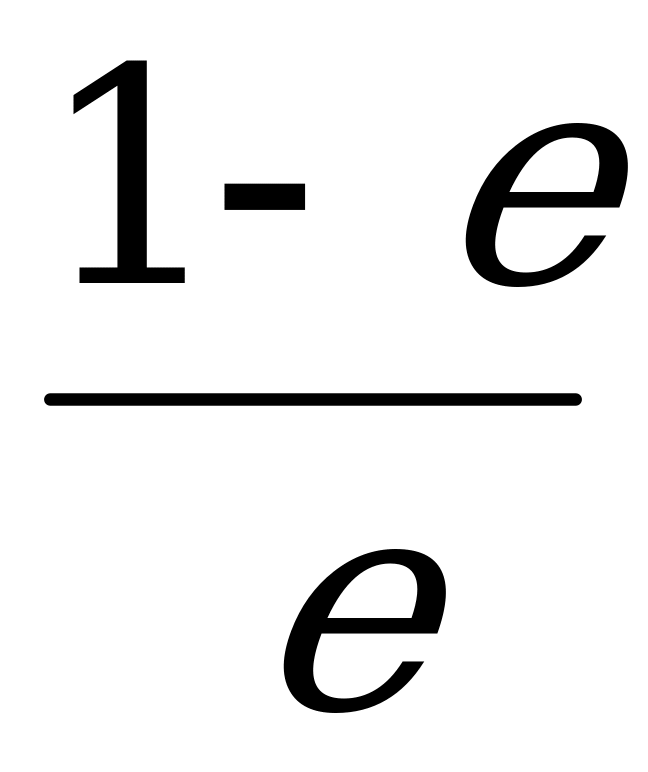 .
.
Часть 2.
В1. Найдите значение выражения 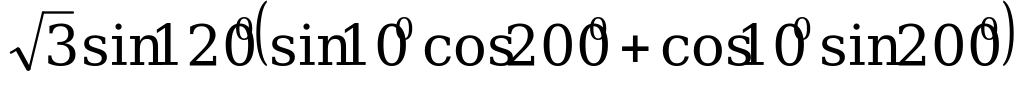 .
.
В2. Решите уравнение 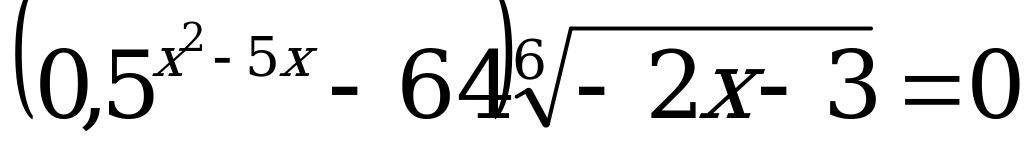 .
.
В3. Найдите значение выражения  , где
, где  – площадь фигуры, ограниченной линиями
– площадь фигуры, ограниченной линиями 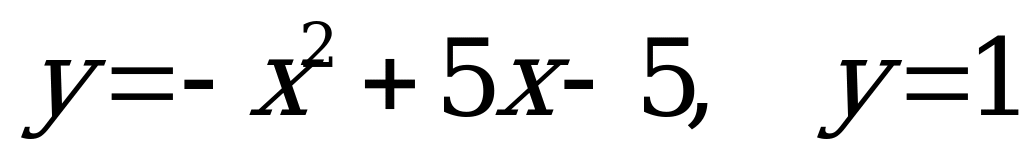 .
.
В4. На рисунке изображен график производной функции 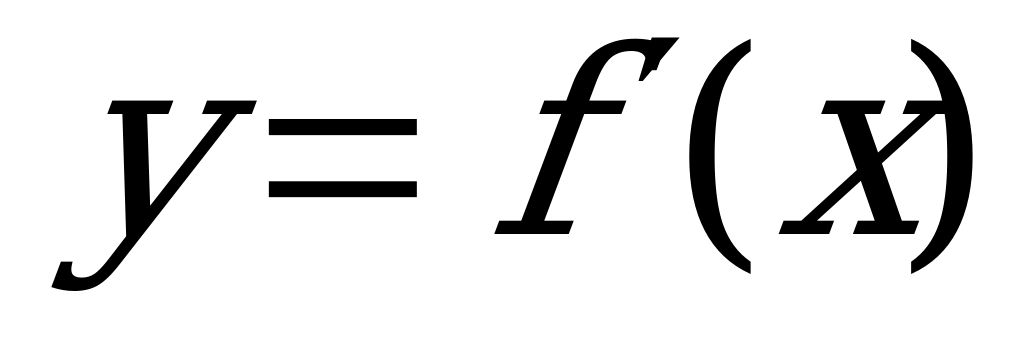 , заданной на отрезке
, заданной на отрезке 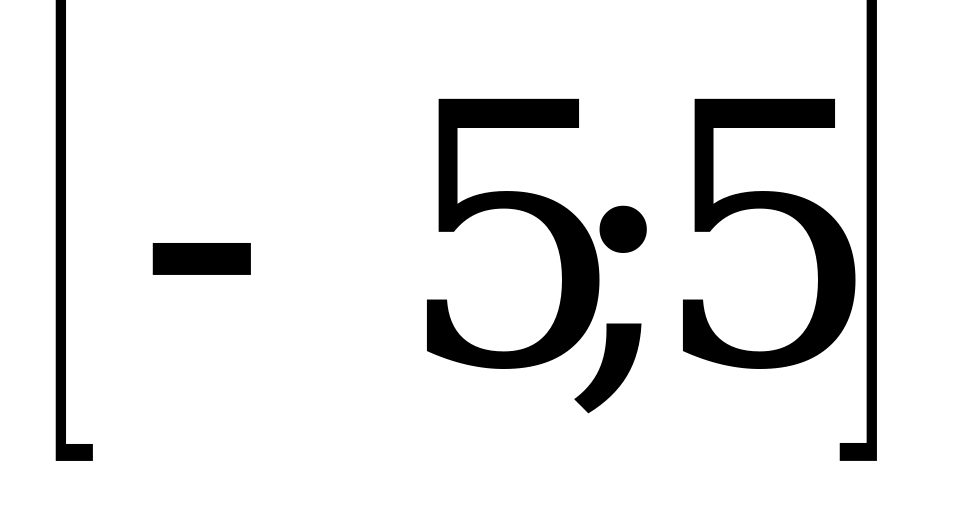 . Укажите число точек максимума функции
. Укажите число точек максимума функции 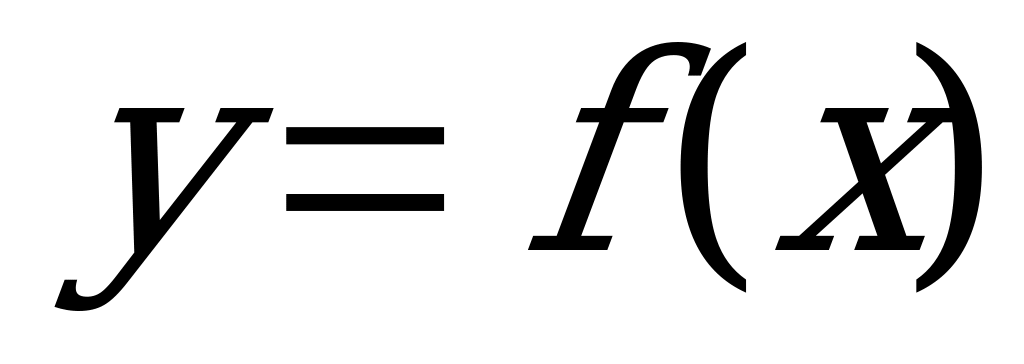 .
.
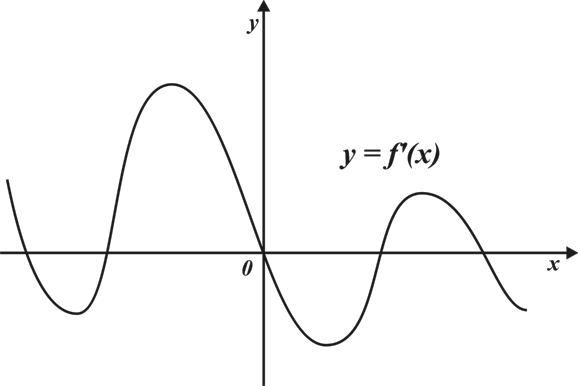
В5. Найдите наибольшее значение функции 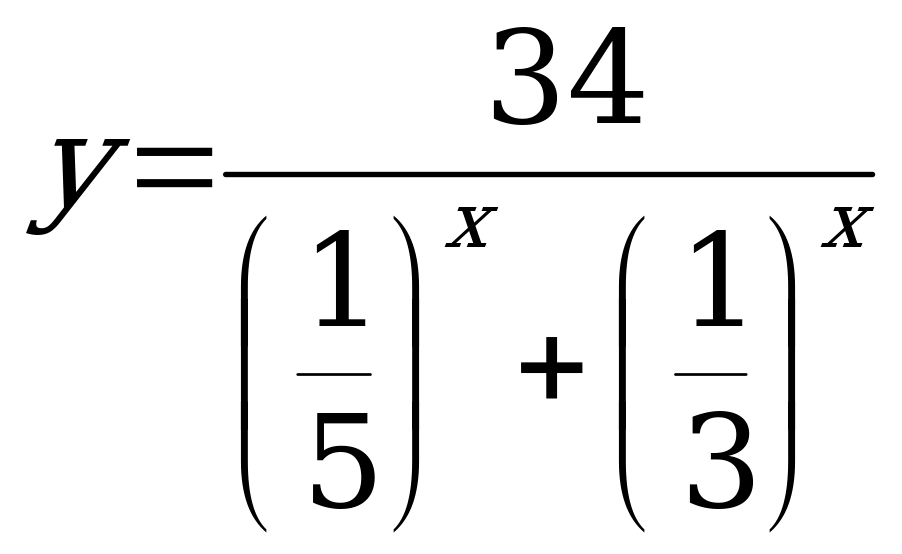 на промежутке
на промежутке 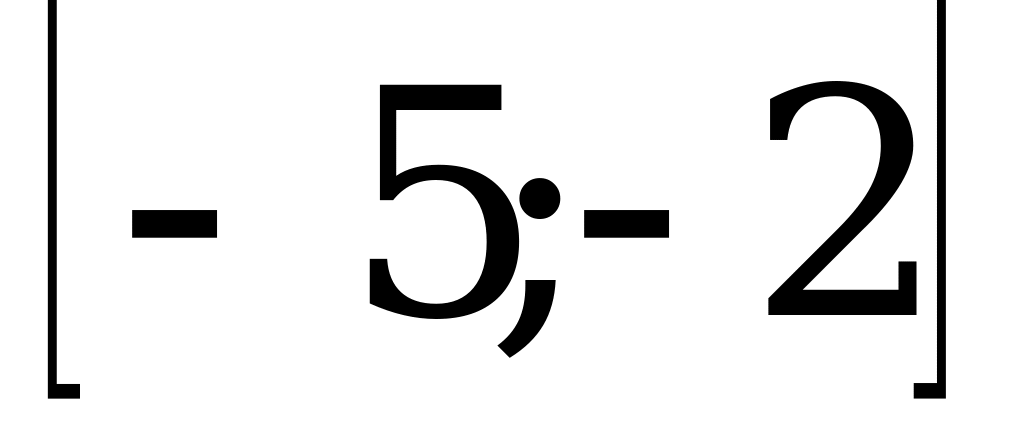 .
.
В6. Найдите сумму всех целых чисел, входящих в область определения функции 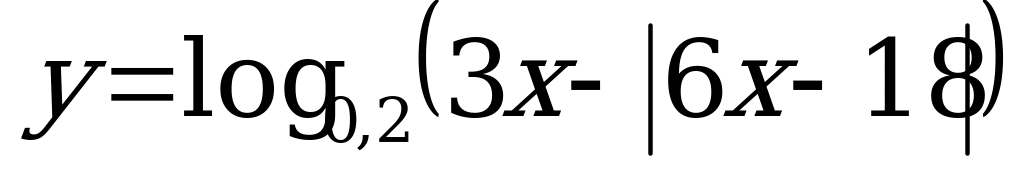 .
.
В7. Группа туристов в первый день путешествия прошла 10 км. Далее туристы решили преодолевать на 5 км больше, чем в предшествующий день, пользуясь при этом, если потребуется автостопом. В результате они преодолели 450 км. Сколько дней туристы были на маршруте, если в течение этого времени 8 дней они отдыхали?
В8. Грань ABCD прямоугольного параллелепипеда  – квадрат. Точка
– квадрат. Точка 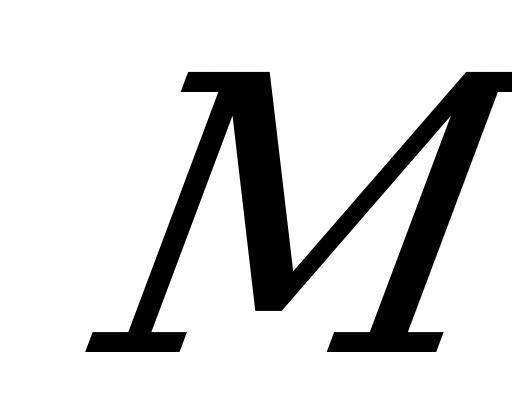 расположена на ребре
расположена на ребре 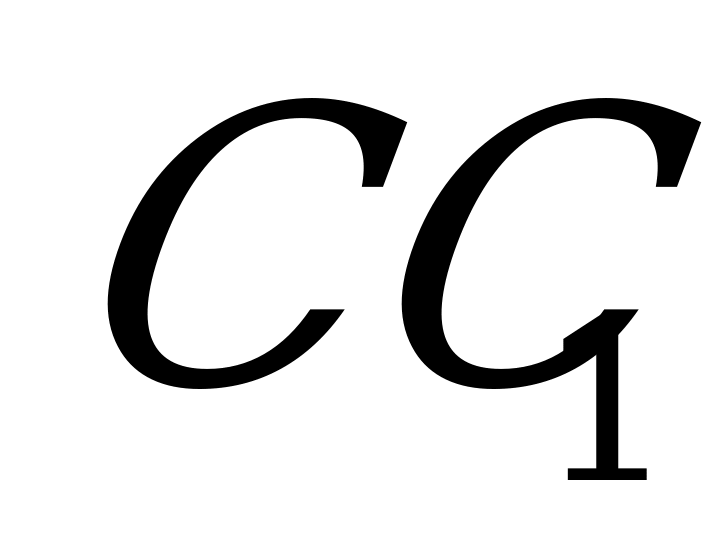 так, что
так, что 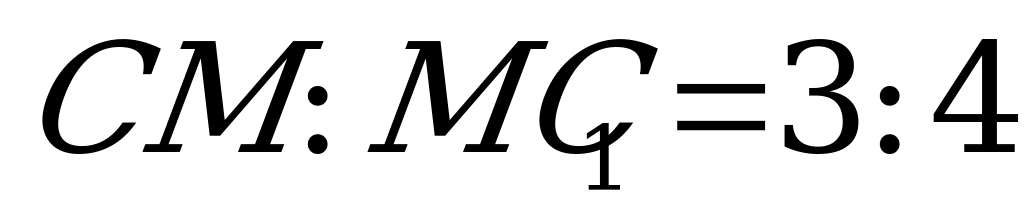 и угол между плоскостями
и угол между плоскостями 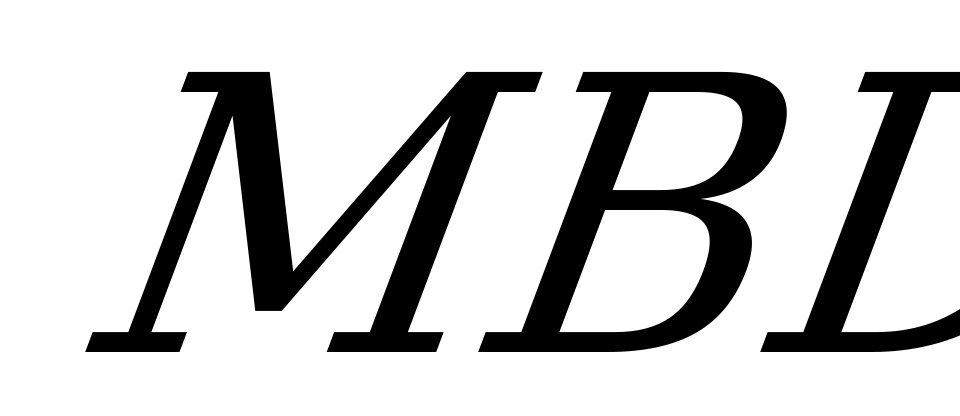 и
и 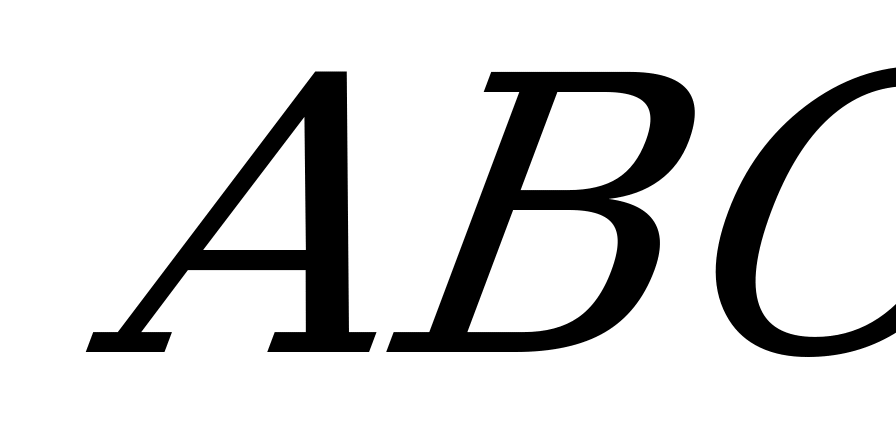 равен
равен 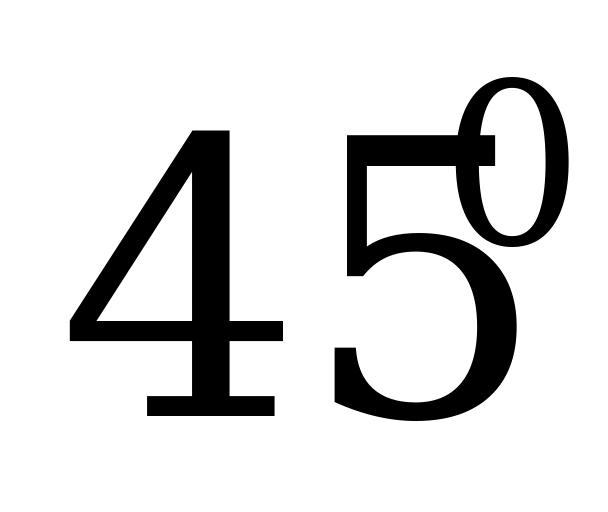 . Найдите объем призмы, если
. Найдите объем призмы, если 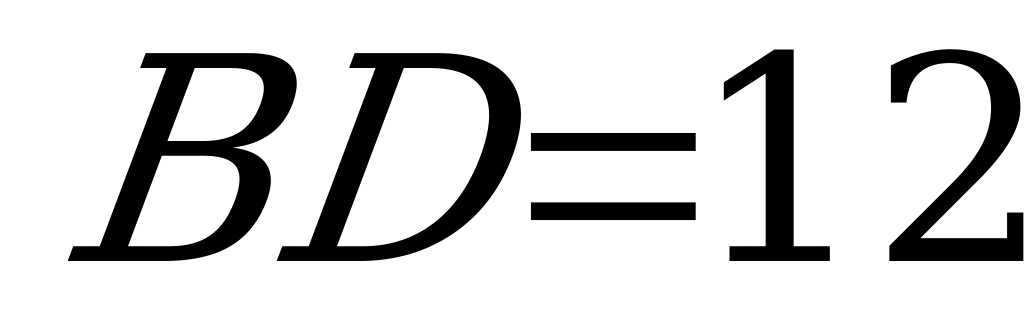 .
.
В9. Биссектриса угла 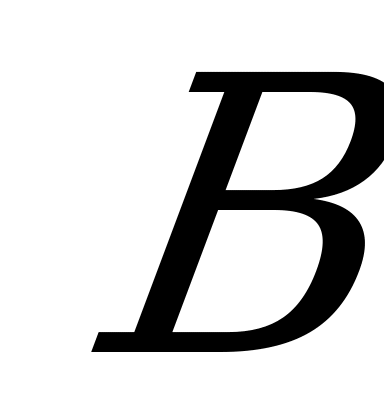 пересекает сторону
пересекает сторону 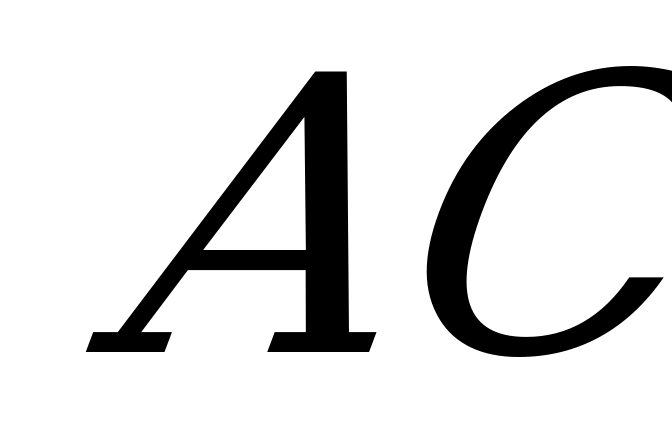 треугольника
треугольника 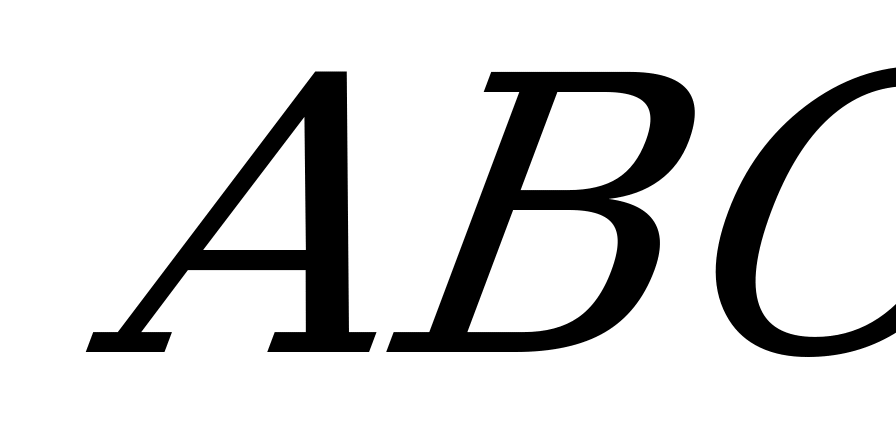 в точке
в точке 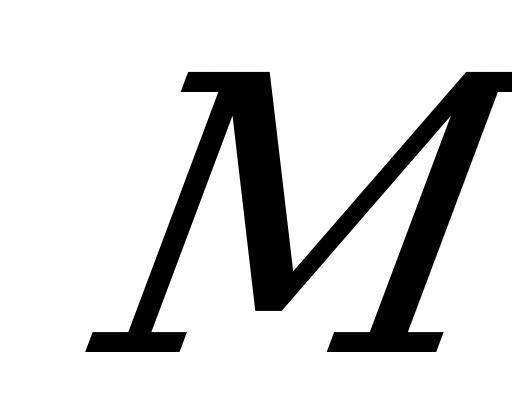 и делит ее на отрезки
и делит ее на отрезки 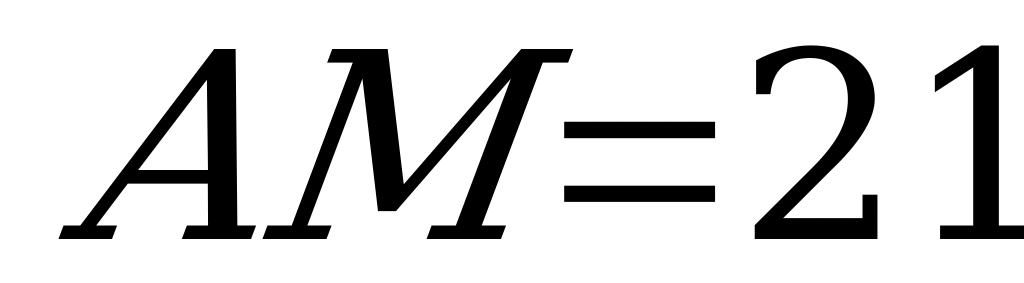 и
и 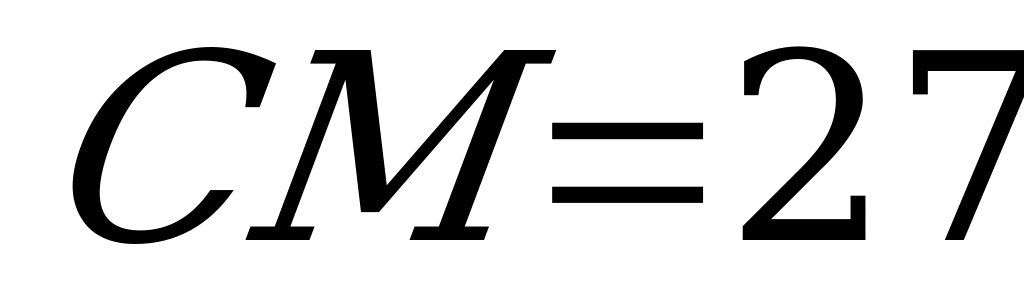 . Найдите периметр треугольника
. Найдите периметр треугольника 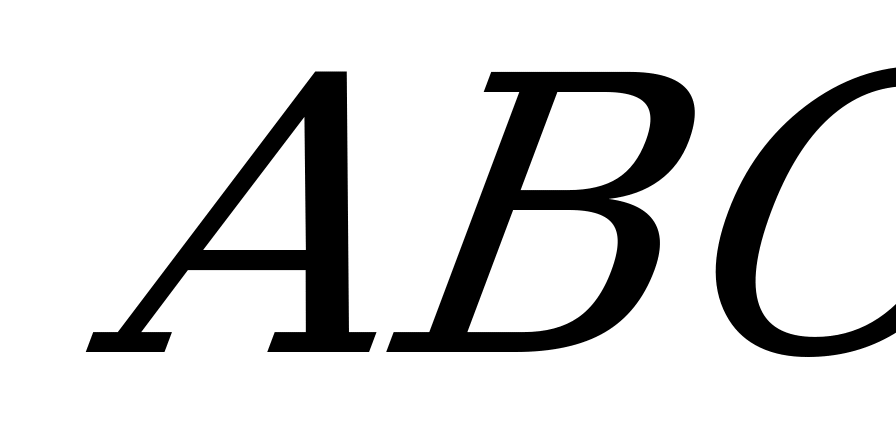 , если биссектриса угла
, если биссектриса угла 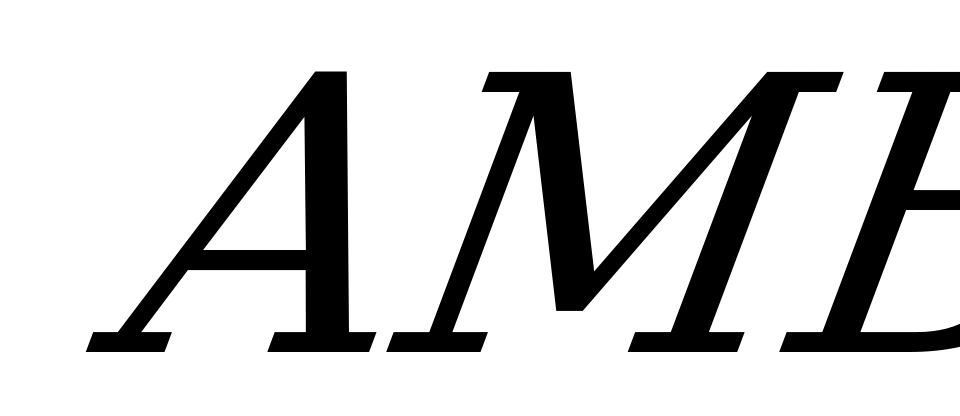 перпендикулярна прямой
перпендикулярна прямой 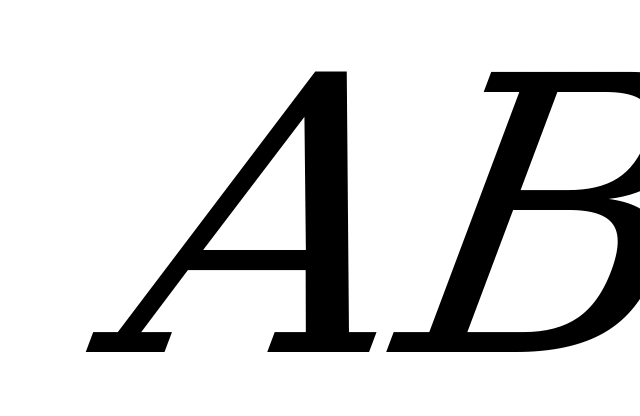 .
.
Часть 3.
С1. Решите систему уравнений 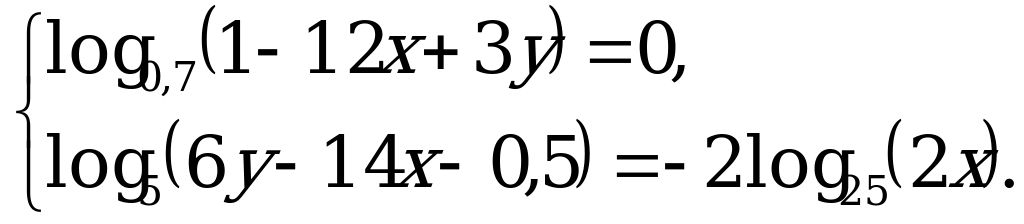
С2. В треугольнике 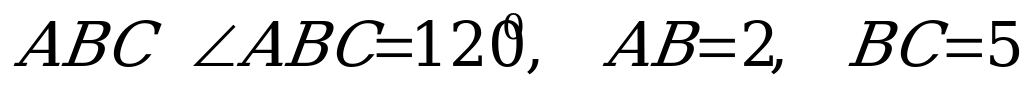 . Найдите наибольшее значение площади треугольника
. Найдите наибольшее значение площади треугольника 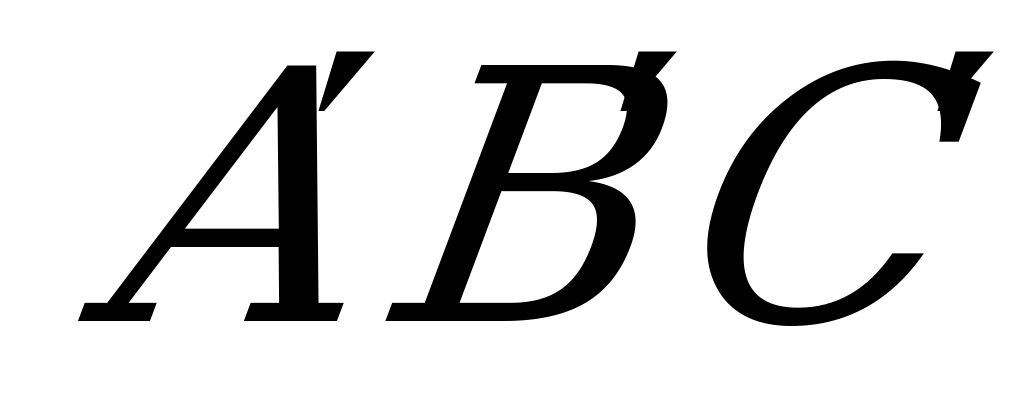 , если его периметр равен 10, а точки
, если его периметр равен 10, а точки  и
и 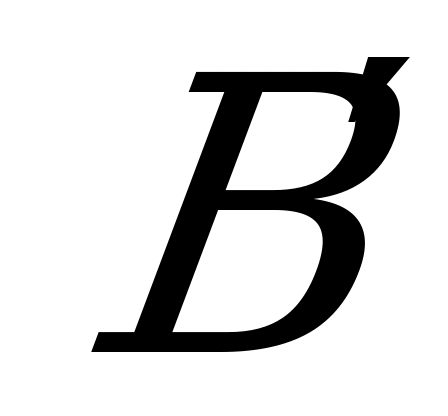 лежат соответственно на сторонах
лежат соответственно на сторонах 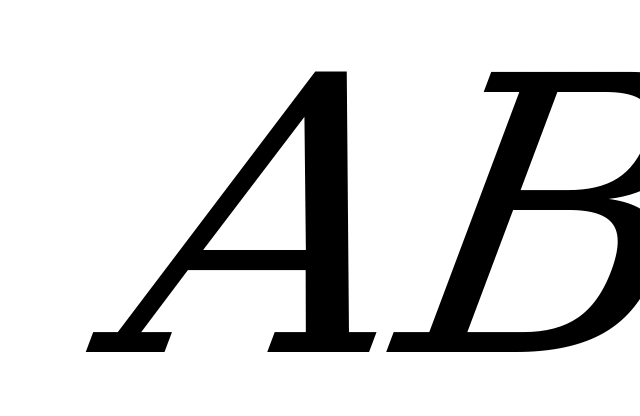 и
и 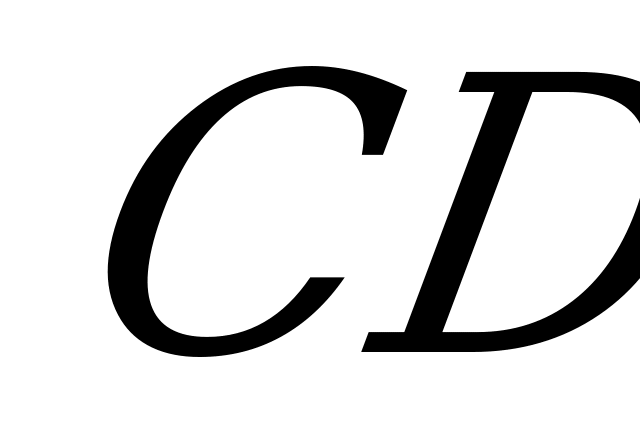 .
.
С3. Диаметр основания и образующая конуса равны 4. Внутри конуса расположен шар. Этот шар касается основания конуса в точке  . Расстояние
. Расстояние 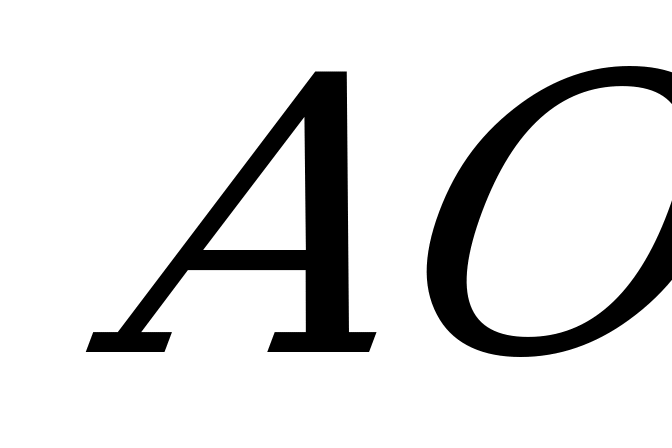 , где О – центр основания конуса, равно 1,5. Плоскость
, где О – центр основания конуса, равно 1,5. Плоскость  , касающаяся поверхности шара, проходит через вершину конуса и пересекает его основание по хорде, перпендикулярной прямой
, касающаяся поверхности шара, проходит через вершину конуса и пересекает его основание по хорде, перпендикулярной прямой 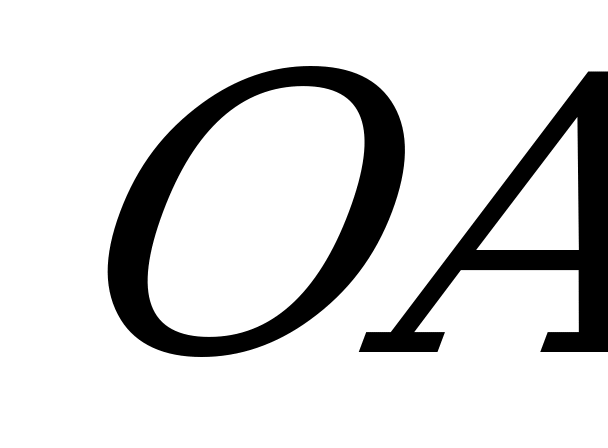 . Найдите косинус угла между плоскостью
. Найдите косинус угла между плоскостью  и плоскостью основания конуса.
и плоскостью основания конуса.
С4. Найдите все значения параметра 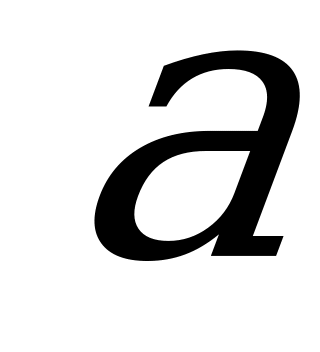 , при которых множество решений неравенства
, при которых множество решений неравенства 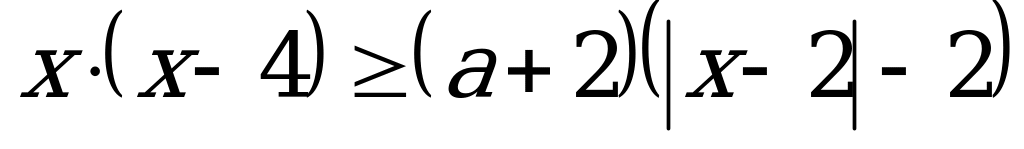 включает все члены некоторой арифметической прогрессии, содержащей как отрицательные, так и положительные члены, а разность этой прогрессии равна 0,5.
включает все члены некоторой арифметической прогрессии, содержащей как отрицательные, так и положительные члены, а разность этой прогрессии равна 0,5.
Ответы к тренировочному варианту.
Ответы к заданиям части А.
| Задание | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| № ответа | 3 | 4 | 2 | 3 | 3 | 2 | 4 | 3 | 1 | 1 | 3 | 4 | 3 | 2 |
Ответы к заданиям части В.
| Задание | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Ответ | 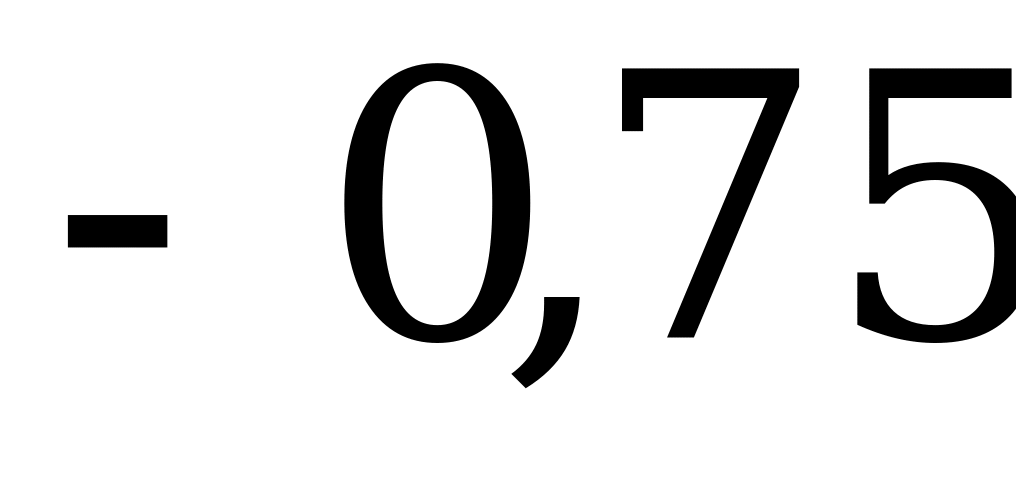
| 1,5 | 1 | 3 | 1 | 12 | 20 | 126 | 112 |
Ответы к заданиям части С.
25







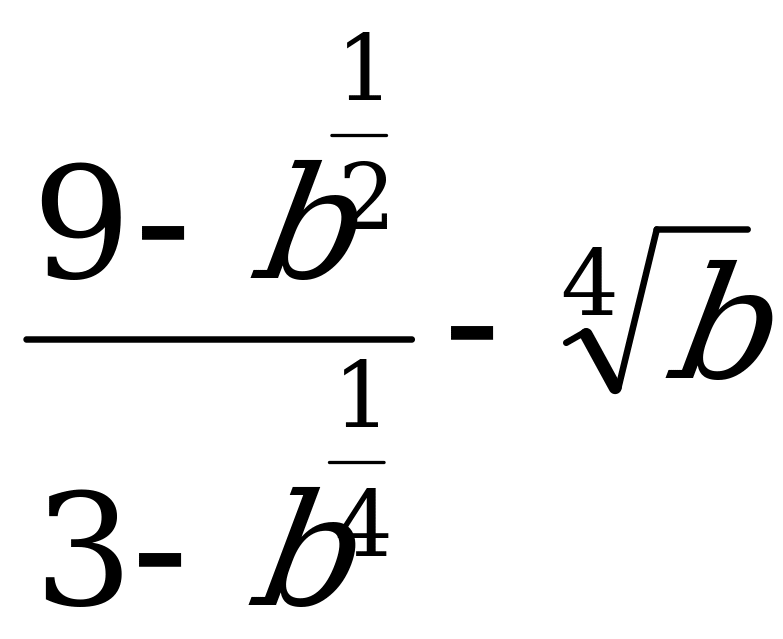 .
.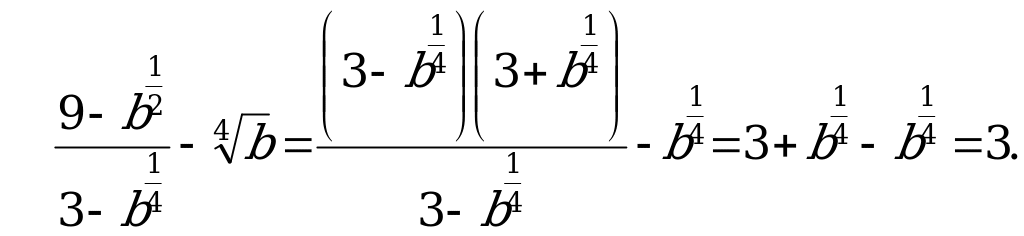

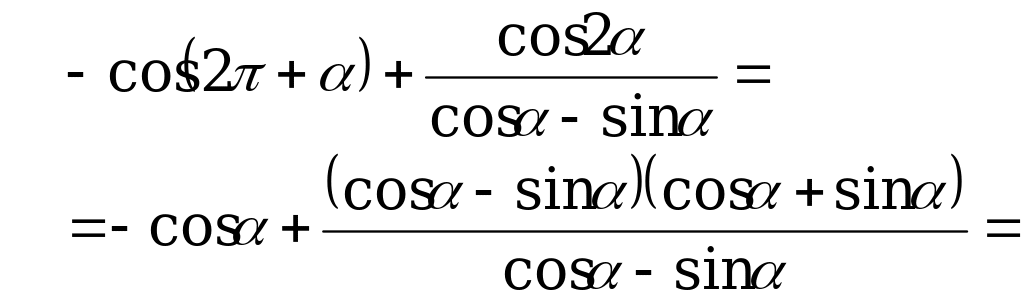


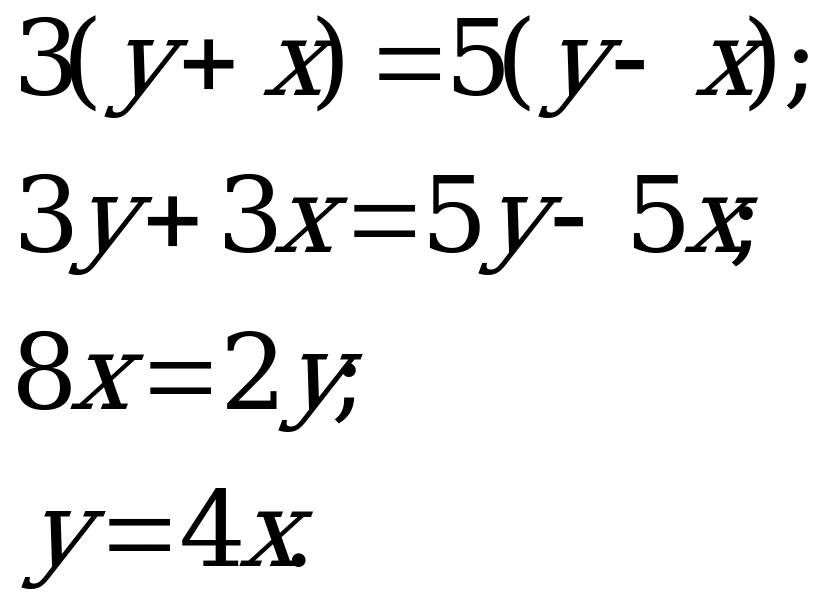
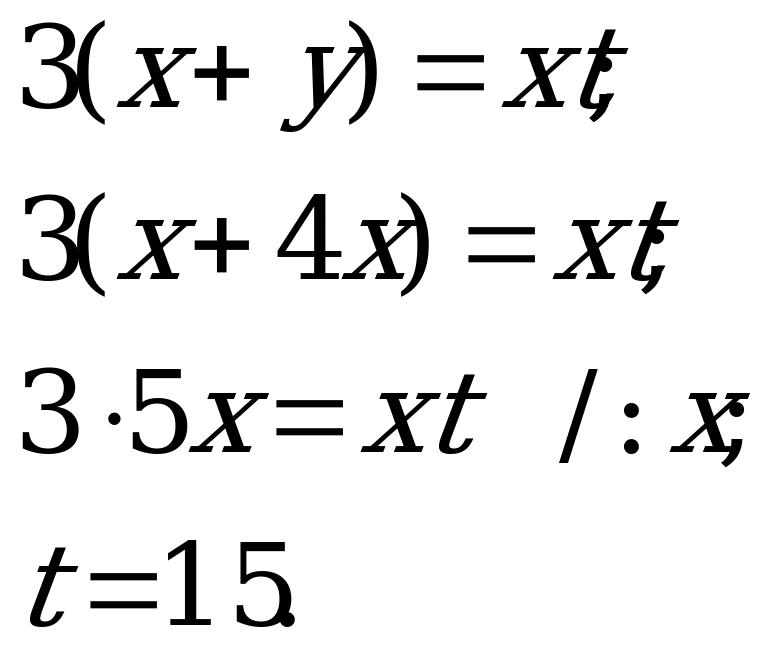
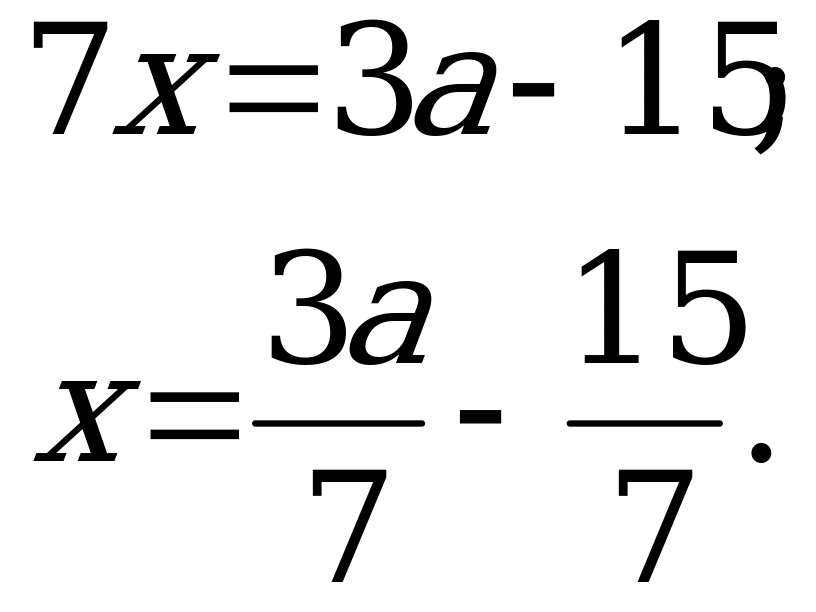
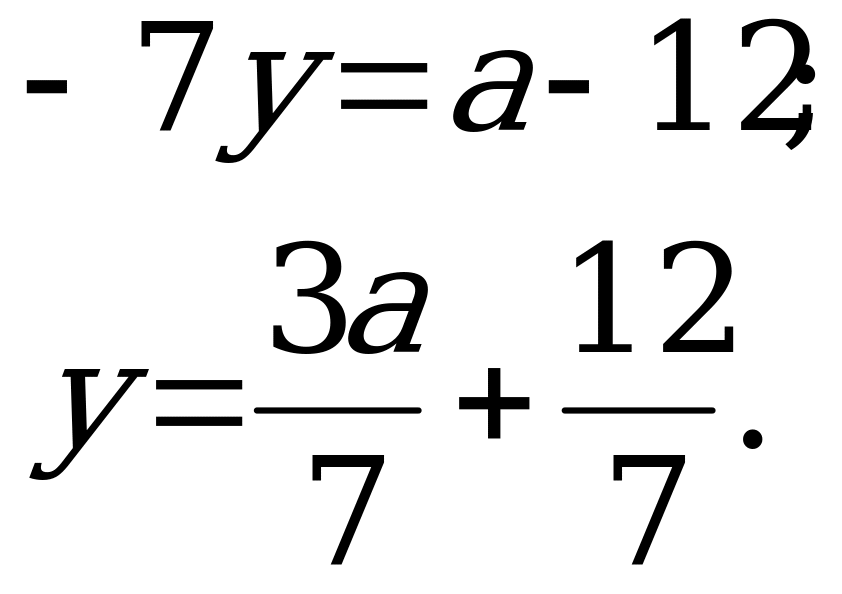

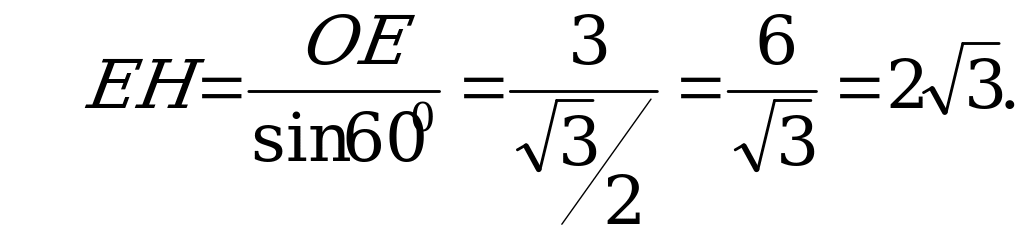

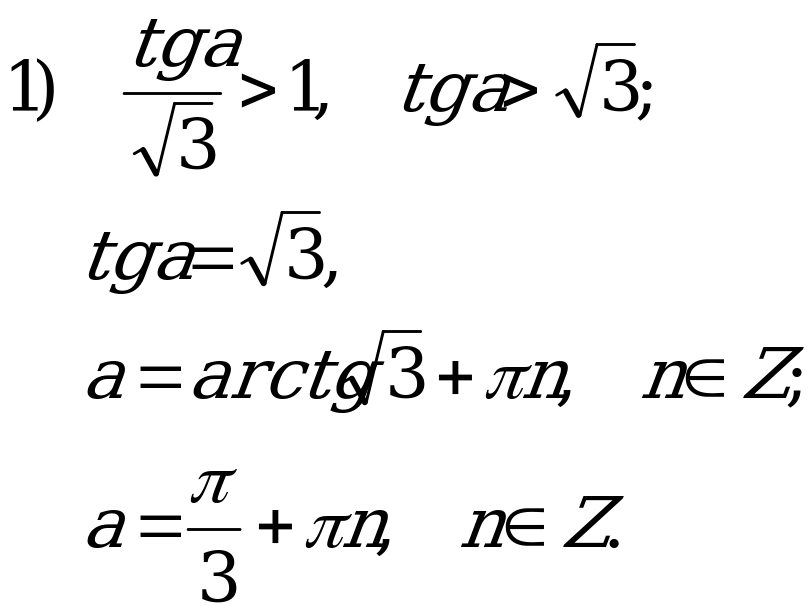
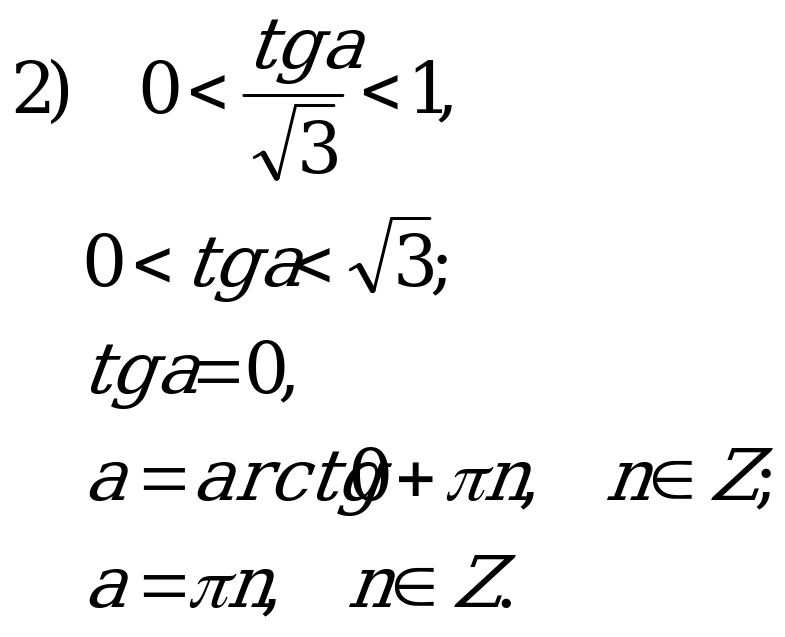
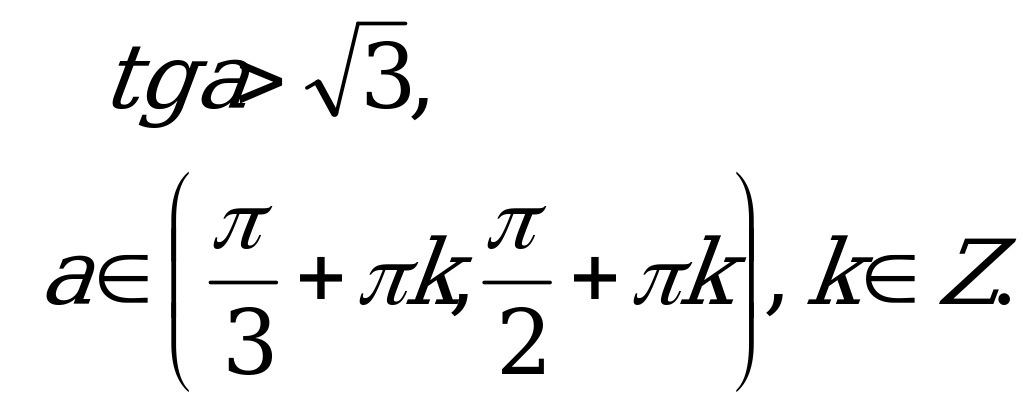
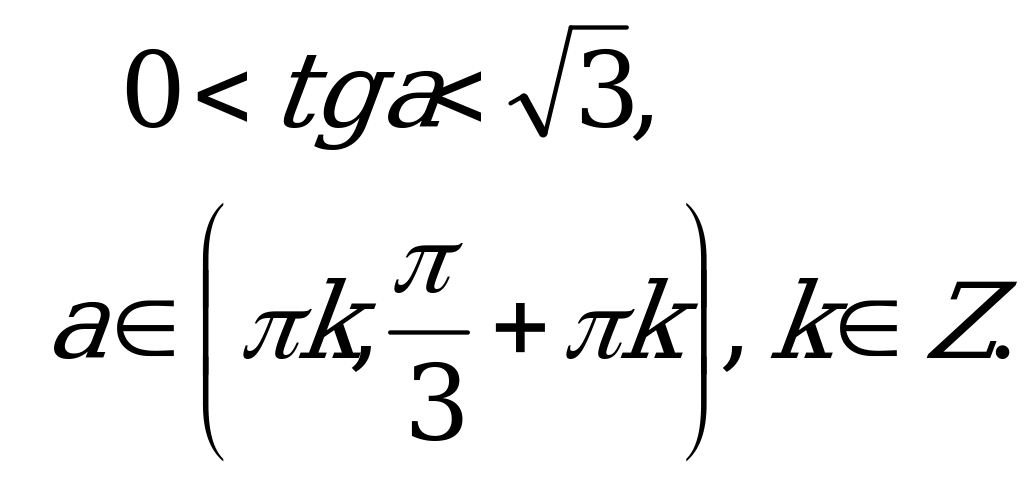
 или
или 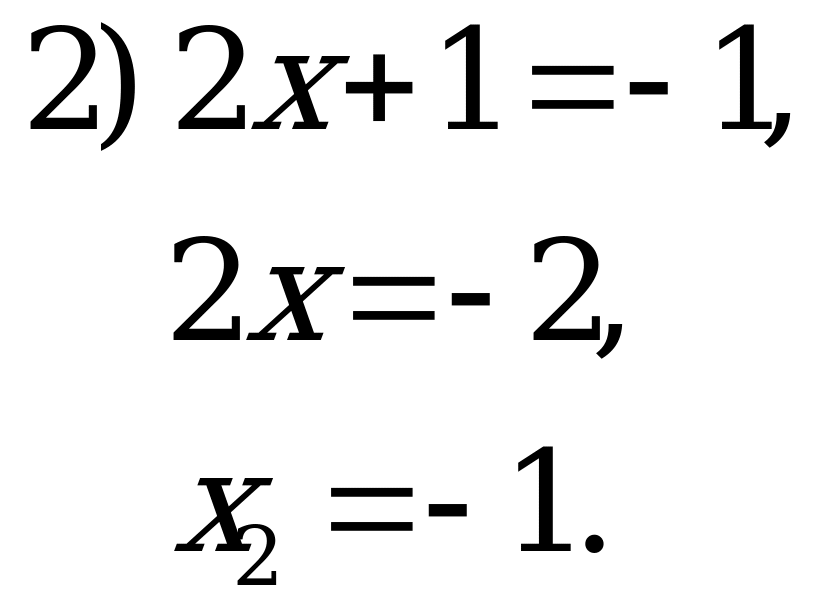





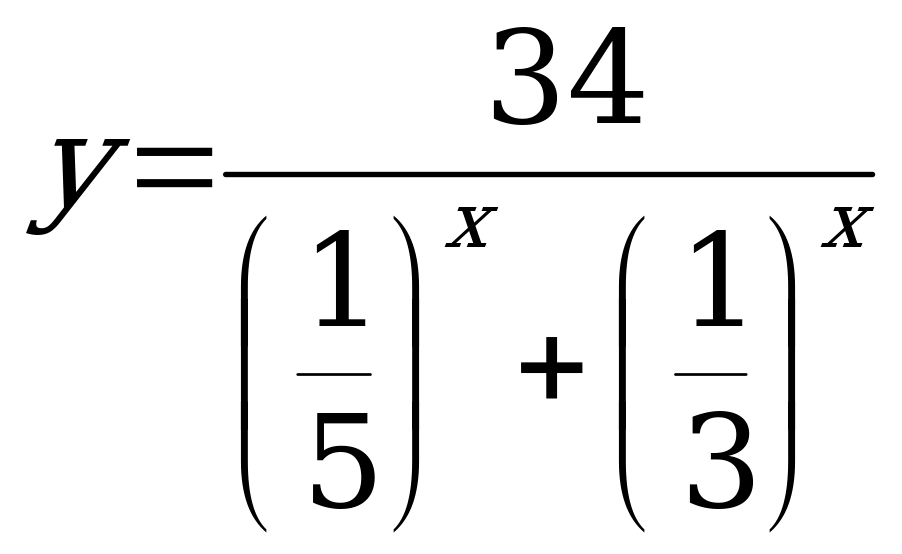 на промежутке
на промежутке 









