| 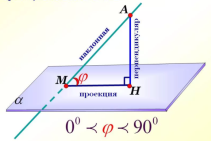 Определение угла между прямой и плоскостью Определение угла между прямой и плоскостью
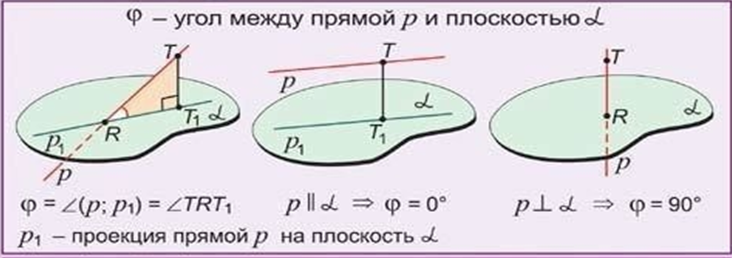
| Углом между прямой и плоскостью называется угол между прямой и её проекцией на эту плоскость
|
| алгоритм построения угла между прямой и плоскостью при решении задач | -
найти какую-нибудь удобную точку на прямой, опустить перпендикуляр на плоскость, -
выяснить, что из себя представляет проекция, -
решать планиметрическую задачу по поиску угла в треугольнике (зачастую прямоугольном). |
| Если прямая перпендикулярна плоскости, то угол между ними 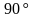 . . | Если прямая параллельна плоскости, то угол между ними 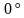 . .
|
| 
|
| Постройте в правильной треугольной пирамиде
| у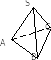 гол между ребром SA и плоскостью ABC гол между ребром SA и плоскостью ABC
| у гол между ребром SB и плоскостью ASC гол между ребром SB и плоскостью ASC
| у гол между ребром AB и плоскостью SBC гол между ребром AB и плоскостью SBC
|
|
|
Некоторые формулы, используемые для решения задач методом координат |
| 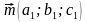 - направляющий вектор прямой - направляющий вектор прямой
Общее уравнение плоскости: 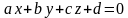
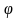 - угол между прямой и плоскостью - угол между прямой и плоскостью
| 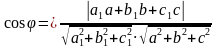
Синус угла 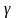 между прямой и плоскостью равен косинусу угла между прямой и плоскостью равен косинусу угла 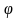 между нормалью к плоскости и направляющим вектором прямой между нормалью к плоскости и направляющим вектором прямой
|
| 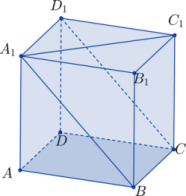 Типовая задача Типовая задача
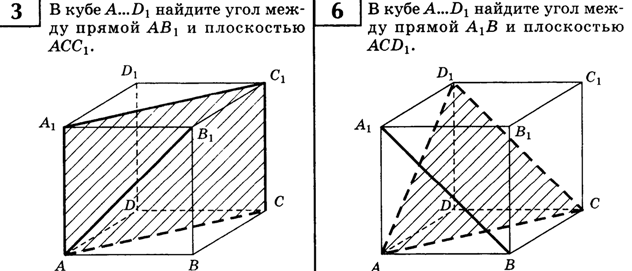
| Дан куб 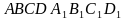 . Чему равен угол между . Чему равен угол между  и плоскостью и плоскостью 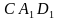 ? ? Ответ: 350
|
| Опорная задача 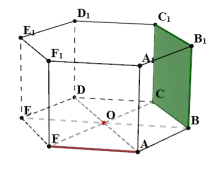
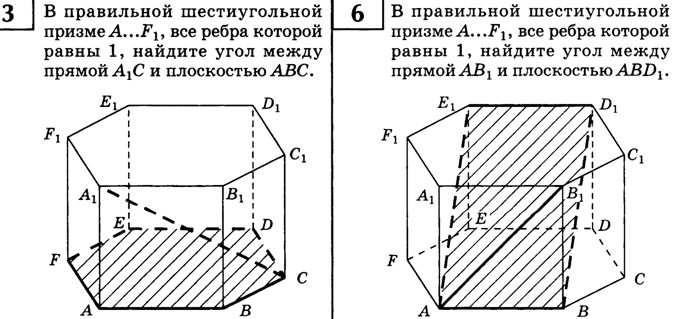
| В правильной шестиугольной призме, все ребра которой равны 1, найдите угол между прямой  и плоскостью и плоскостью  . . Решение 1.Проводим прямую 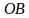 . параллельно прямой . параллельно прямой  , поэтому угол между прямой , поэтому угол между прямой  и плоскостью и плоскостью  будет равен углу между прямой будет равен углу между прямой 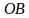 и плоскостью и плоскостью  -
2. Опускаем на плоскость  перпендикулярную ей прямую перпендикулярную ей прямую 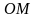 . . 3 7 .Проводим через точки 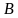 и и  прямую прямую 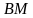 . Эта прямая является проекцией прямой . Эта прямая является проекцией прямой 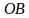 на плоскость на плоскость  4.По определению, углом между прямой 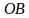 и плоскостью и плоскостью  будет угол будет угол  между прямой между прямой 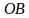 ее проекцией ее проекцией 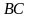 . . 5. Находим 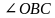 : : По свойствам правильной шестиугольной призмы треугольник OCB является правильным треугольником. Все углы правильного треугольника равны 60 градусам. Следовательно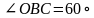 Ответ:  |
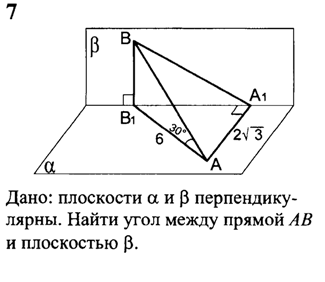
| найти угол между прямой 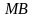 и плоскостью и плоскостью  | 2
|
| 1 
|  
|
| 4 3 
| 
|
|
|
|
|
|
|
6
5
8
Ответы на задания по готовым чертежам:
1 способ (геометрический):
Сечение плоскостью A1BC есть прямоугольник A1BCD1.
Из точки C1 проведем перпендикуляр C1H к CD1. BH — проекция BC1на плоскость A1BC. Значит, нужно найти угол C1BH.
В прямоугольном треугольнике D1C1C находим:
В прямоугольном треугольнике BCC1 находим: BC1 = 17.
В прямоугольном треугольнике C1HB находим: 
Ответ:
Задание из открытого банка задач ЕГЭ
В прямоугольном параллелепипеде 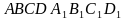 найдите угол между плоскостью
найдите угол между плоскостью  и прямой
и прямой  , если
, если
2 способ (аналитический):
-
Введем систему координат с началом в точке  тогда
тогда
-
Найдем уравнение плоскости  :
:
, тогда
Тогда уравнение плоскости  принимает вид:
принимает вид:
|∙24
-
направляющий вектор прямой  :
: 
-
Тогда по формуле угла косинуса угла между направляющим вектором и нормалью плоскостями получаем:
Ответ: .
Муниципальное бюджетное общеобразовательное учреждение города Мурманска «Лицей №2»
«Угол между прямой и плоскостью»
Мурманск, 2020 г.








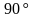 .
.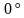 .
.
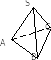 гол между ребром
гол между ребром  гол между ребром
гол между ребром 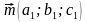 - направляющий вектор прямой
- направляющий вектор прямой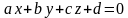
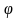 - угол между прямой и плоскостью
- угол между прямой и плоскостью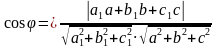
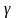 между прямой и плоскостью равен косинусу угла
между прямой и плоскостью равен косинусу угла 
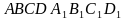 . Чему равен угол между
. Чему равен угол между  и плоскостью
и плоскостью 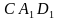 ?
?
 и плоскостью
и плоскостью  .
.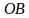 . параллельно прямой
. параллельно прямой 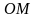 .
.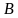 и
и  прямую
прямую 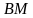 . Эта прямая является проекцией прямой
. Эта прямая является проекцией прямой  между прямой
между прямой 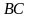 .
.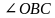 :
: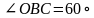

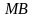 и плоскостью
и плоскостью 







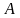 к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках
к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках 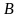 и
и  . Верно ли утверждение: «
. Верно ли утверждение: « , если
, если  »?
»? .
.  .
.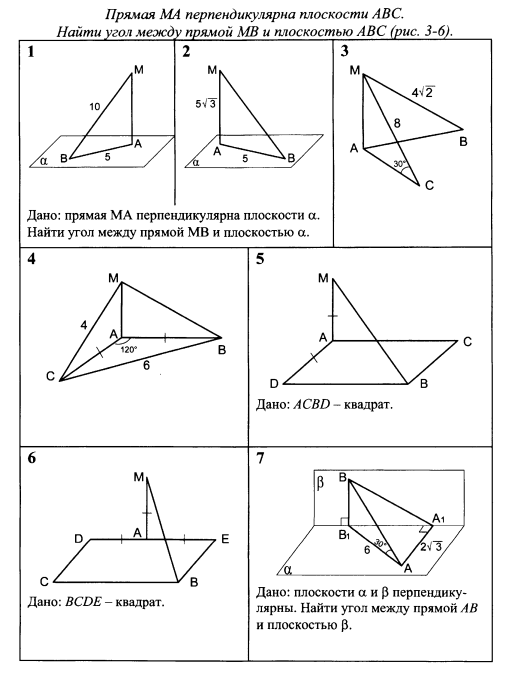



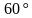
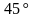


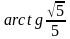

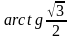

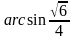
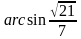

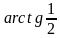
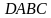 —прямоугольный треугольник
—прямоугольный треугольник  . Высота пирамиды проходит через точку
. Высота пирамиды проходит через точку 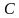 . Найти углы, которые образуют боковые рёбра
. Найти углы, которые образуют боковые рёбра  и
и 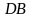 с плоскостью основания, если
с плоскостью основания, если 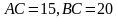 , а угол между плоскостями
, а угол между плоскостями 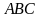 и
и 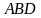 равен
равен 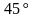
 треугольной пирамиды
треугольной пирамиды 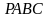 с вершиной
с вершиной 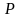 проходит через точку
проходит через точку  и
и 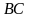 перпендикулярны. Найти углы, которые образуют боковые рёбра
перпендикулярны. Найти углы, которые образуют боковые рёбра 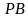 с плоскостью основания, если
с плоскостью основания, если  а расстояние от точки
а расстояние от точки 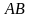 равно
равно  .
.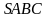 с основанием
с основанием 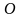 —точка пересечения медиан треугольника
—точка пересечения медиан треугольника 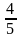 от высоты
от высоты 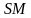 боковой грани
боковой грани 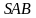 .
.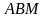 , если пирамида правильная, а угол между прямой, проходящей через точку
, если пирамида правильная, а угол между прямой, проходящей через точку 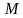 и середину ребра
и середину ребра  равен
равен  , в котором
, в котором  . Точка
. Точка 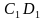 , точка N лежит на ребре
, точка N лежит на ребре 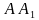 , причём
, причём  . Найти угол между прямой
. Найти угол между прямой 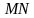 и плоскостью грани
и плоскостью грани  .
.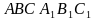 , основание которой—прямоугольный треугольник
, основание которой—прямоугольный треугольник  пересекает плоскость
пересекает плоскость 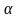 . На прямой
. На прямой  , причем известно, что проекция этого отрезка на плоскость
, причем известно, что проекция этого отрезка на плоскость 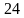 . Найдите синус угла между прямой
. Найдите синус угла между прямой 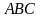 – правильный треугольник со стороной 3,
– правильный треугольник со стороной 3, 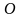 – точка, лежащая вне плоскости треугольника, причем
– точка, лежащая вне плоскости треугольника, причем  . Найдите угол, который образуют прямые
. Найдите угол, который образуют прямые  с плоскостью треугольника. Ответ дайте в градусах.
с плоскостью треугольника. Ответ дайте в градусах.
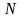 – середина ребра
– середина ребра 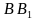 , а точка
, а точка 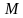 – середина отрезка
– середина отрезка 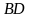 . Найдите
. Найдите 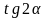 , где
, где  и плоскостью
и плоскостью 
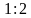 , считая от вершины
, считая от вершины 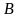 . Найдите
. Найдите 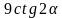 , где
, где 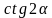 , если
, если  . Вне плоскости треугольника отмечена точка
. Вне плоскости треугольника отмечена точка 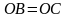 и
и 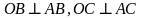 . Известно, что
. Известно, что 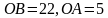 . Найдите косинус угла между прямой
. Найдите косинус угла между прямой  и плоскостью треугольника.
и плоскостью треугольника.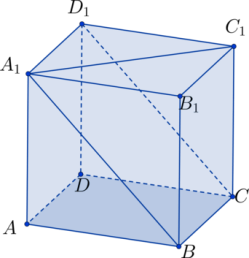
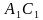 и плоскостью
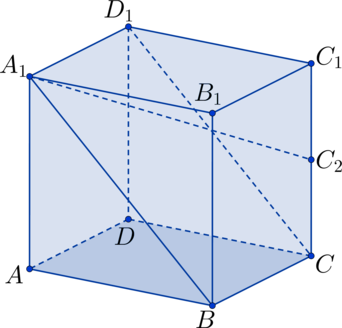
и плоскостью 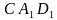 ?
?
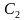 – середина стороны
– середина стороны  . Чему равен квадрат котангенса угла между
. Чему равен квадрат котангенса угла между  и плоскостью
и плоскостью 
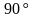 .
.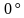 .
.




















