|  Определение угла между прямыми Определение угла между прямыми
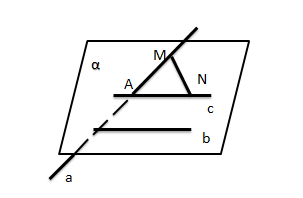
| Углом между скрещивающимися прямыми называют угол, который образуется между двумя прямыми, параллельными заданным скрещивающимся прямым.
|
| алгоритм построения угла между скрещивающимися прямыми при решении задач | Алгоритм решения: -
Определение типа прямых. -
Параллельный перенос одной или обеих прямых. -
Нахождение требуемого угла. |
|
|
| 
|
| Постройте в правильной треугольной пирамиде
| у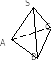 гол между ребрами гол между ребрами SA и AC
|  угол между ребром CD и прямой угол между ребром CD и прямой 
| угол между ребром AB и прямой  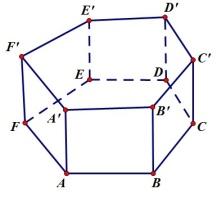
|
|
| Некоторые формулы, используемые для решения задач методом координат |
| 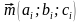 - направляющий вектор прямой - направляющий вектор прямой
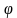 - угол между прямыми - угол между прямыми
| 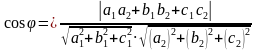
|
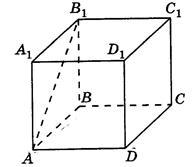
| 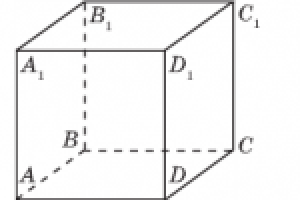 Типовая задача Типовая задача
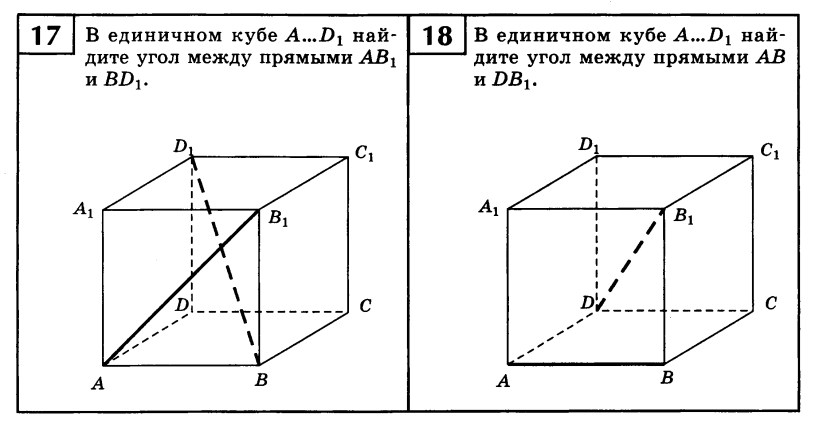
| Дан куб 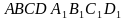 . . -
 -
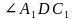 -
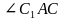 -
угол между прямыми  и и 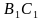 -
угол между прямыми  и и  Ответ: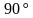 ; ; 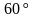 ; ;  ; ; 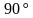 ; ;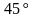 |
| Опорная задача 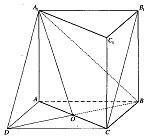
| Найти косинус угла между скрещивающимися диагоналями двух боковых граней правильной треугольной призмы, боковое ребро которой равно стороне основания. Решение Через вершину  проведем прямую, которая параллельна диагонали проведем прямую, которая параллельна диагонали  . Точка . Точка  пересечение пересечение  с плоскостью с плоскостью 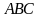 . . 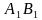  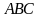 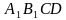 , значит , значит 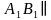 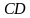 , а , а 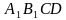 -параллелограмм. -параллелограмм.  , значит, , значит, 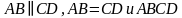 -ромб. -ромб. диагонали ромба АС и ВD пересекаются под прямым углом в точке О и делятся пополам, значит,  в равнобедренном треугольнике в равнобедренном треугольнике 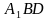 является биссектрисой, медианой и высотой. Угол между диагоналями является биссектрисой, медианой и высотой. Угол между диагоналями  и и  равен углу равен углу . Исходя из условия . Исходя из условия  обозначим через обозначим через 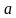 , , тогда диагональ квадрата 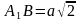 высота равностороннего треугольника   . .
Ответ:  |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Ответы на задания по готовым чертежам:
1 способ (геометрический):
Примем ребро куба за 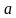 Тогда
Тогда 
Поскольку  , получаем:
, получаем:  и
и
В прямоугольном треугольнике  с прямым углом
с прямым углом  имеем:
имеем:
В прямоугольном треугольнике  с прямым углом
с прямым углом  имеем:
имеем:
В треугольнике  получаем:
получаем:
откуда
Тогда
Ответ:
Задание из открытого банка задач ЕГЭ
На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE : EC1 = 1 : 2.
б) Найдите угол между прямыми BE и AC1.
2 способ (аналитический):
-
Введем систему координат с началом в точке  тогда
тогда
-
направляющий вектор прямой  :
:
-
направляющий вектор прямой  :
: 
-
Тогда по формуле угла косинуса угла между скрещивающимися прямыми получаем:
Ответ: .
Муниципальное бюджетное общеобразовательное учреждение города Мурманска «Лицей №2»
«Угол между скрещивающимися прямыми»
Мурманск, 2020 г.










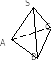 гол между ребрами
гол между ребрами 



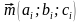 - направляющий вектор прямой
- направляющий вектор прямой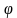 - угол между прямыми
- угол между прямыми 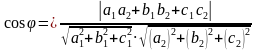

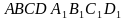 .
. 
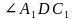
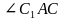
 и
и 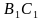
 и
и 
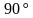 ;
; 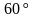 ;
;  ;
; 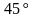

 проведем прямую, которая параллельна диагонали
проведем прямую, которая параллельна диагонали  . Точка
. Точка  пересечение
пересечение 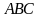 .
. 
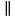
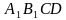 , значит
, значит 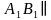
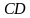 , а
, а  , значит,
, значит, 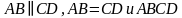 -ромб.
-ромб. в равнобедренном треугольнике
в равнобедренном треугольнике 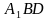 является биссектрисой, медианой и высотой. Угол между диагоналями
является биссектрисой, медианой и высотой. Угол между диагоналями  . Исходя из условия
. Исходя из условия  обозначим через
обозначим через 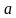 ,
, 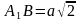

 .
.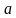 и
и 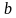 – скрещивающиеся прямые, а прямая
– скрещивающиеся прямые, а прямая  . Верно ли, что угол между прямыми
. Верно ли, что угол между прямыми 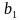 ?
? 
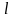 проходит через точку
проходит через точку 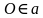 , параллельно прямой
, параллельно прямой 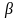 . Верно ли, что угол между прямыми
. Верно ли, что угол между прямыми 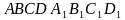
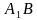 и
и 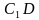 равен 90°?
равен 90°?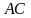 и
и 
 ,
,  и прямоугольный треугольник
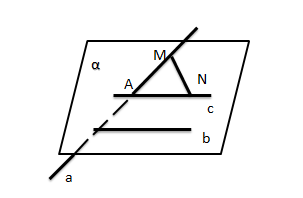
и прямоугольный треугольник 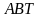 (
( ) расположены в пространстве так, как показано на рисунке. Точки
) расположены в пространстве так, как показано на рисунке. Точки 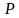 и
и  –середины отрезков
–середины отрезков 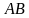 и
и 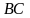 . Верно ли, что угол между прямыми
. Верно ли, что угол между прямыми  и
и 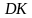 равен 90°?
равен 90°?
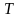 – середины рёбер
– середины рёбер 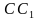 и
и 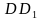 соответственно. Верно ли, что угол между прямыми
соответственно. Верно ли, что угол между прямыми  и
и  равен 90°?
равен 90°?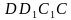 . Верно ли, что угол между прямыми
. Верно ли, что угол между прямыми 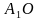 и
и 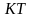 (точки
(точки  и
и 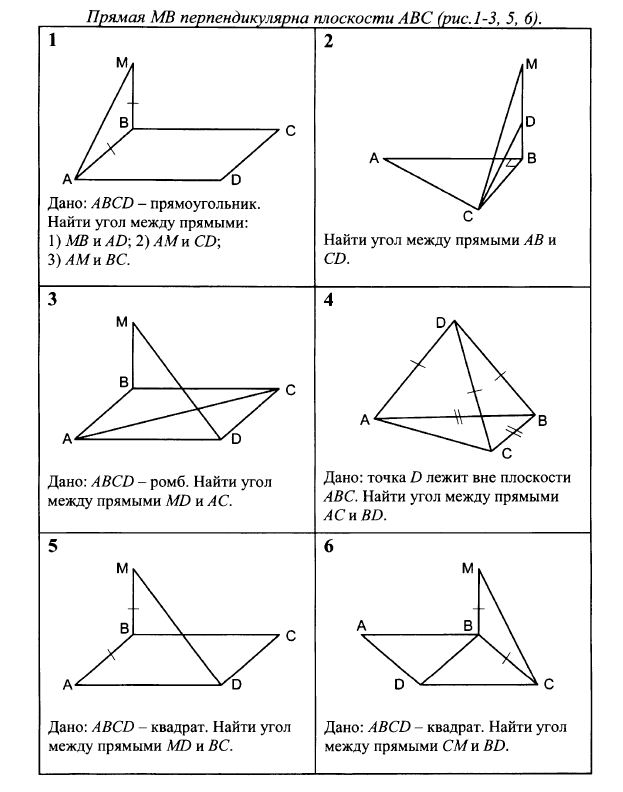

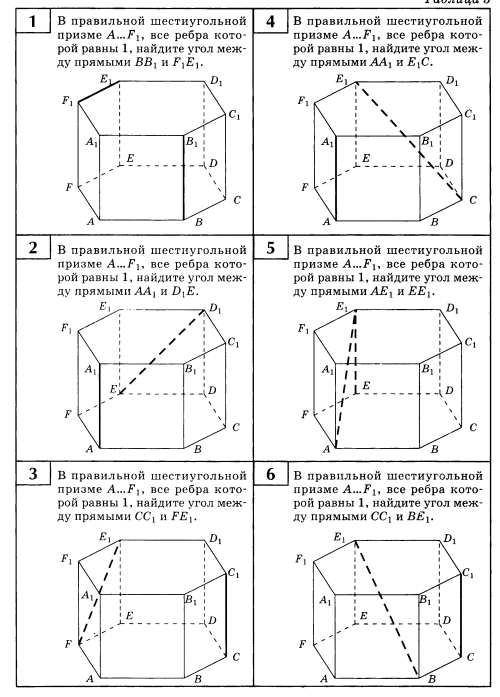
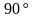
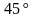
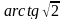
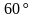
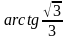


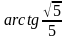
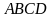 . Найти угол между прямыми
. Найти угол между прямыми 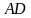 и
и 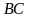 , если
, если 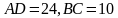 , а расстояние между серединами рёбер
, а расстояние между серединами рёбер  равно
равно 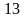 .
.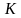 лежит на ребре
лежит на ребре  - точка пересечения плоскости
- точка пересечения плоскости  с ребром
с ребром  и
и 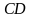 , если
, если  .
. с вершиной
с вершиной  точка
точка  . Найдите угол между прямыми
. Найдите угол между прямыми 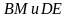 .
.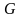 лежит на боковом ребре
лежит на боковом ребре  и
и  , а
, а 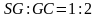 .
.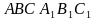 —равносторонние треугольники. Точки
—равносторонние треугольники. Точки 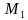 —центры оснований
—центры оснований 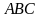 и
и 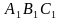 соответственно.
соответственно.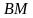 и
и  равен
равен  .
.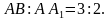
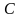 . Точка
. Точка  .
.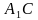 и
и 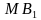 перпендикулярны.
перпендикулярны.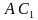 и
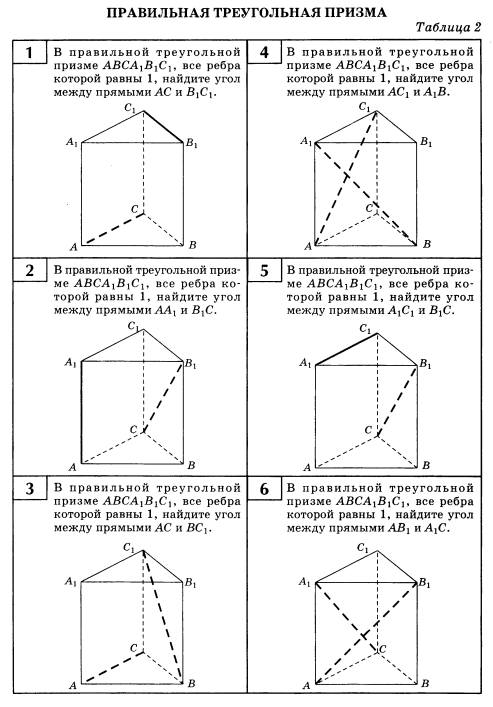
и  со стороной основания
со стороной основания 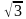 и боковым ребром 1. Найти угол между прямыми
и боковым ребром 1. Найти угол между прямыми 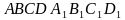 . Найти:
. Найти:
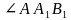
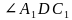
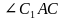
 и
и 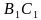
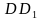 и
и 
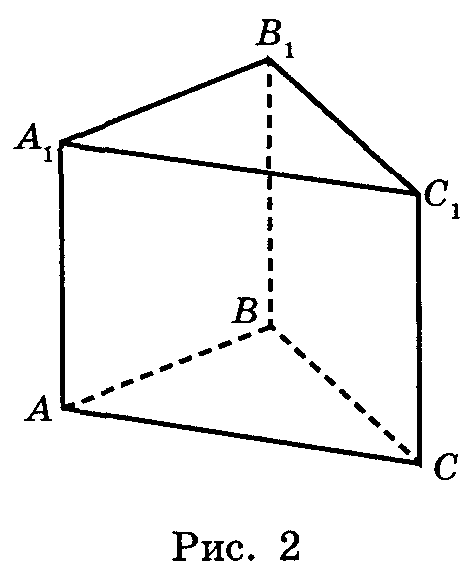
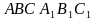 , основаниями которой являются правильные треугольники, а боковыми гранями - квадраты. Найти:
, основаниями которой являются правильные треугольники, а боковыми гранями - квадраты. Найти: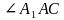
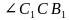
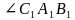


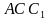 прямоугольного параллелепипеда
прямоугольного параллелепипеда 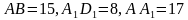 . Ответ дать в градусах.
. Ответ дать в градусах.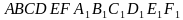 все рёбра равны 31. Найти угол
все рёбра равны 31. Найти угол 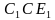 . Ответ дать в градусах.
. Ответ дать в градусах. . Ответ дать в градусах.
. Ответ дать в градусах.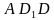 .
. 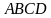 . Найти угол между прямыми
. Найти угол между прямыми 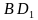 и
и  .
. 
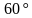

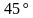











Электронная тетрадь по алгебре 11 класс...
Алгебра 11 класс ФГОС
Электронная тетрадь по алгебре 8 класс...
Алгебра 7 класс
Математика 5 класс ФГОС
Геометрия 9 класс ФГОС
Математика. Вероятность и статистика. 8...
Наглядная геометрия 5-6 классы ФГОС
© 2020, Кришталь Елена Николаевна 8664 216
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы