

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 26.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 27.05.2025 18:34

Хоцкая Наталья Васильевна
учитель математики
56 лет
Местоположение
Россия, г.Донецк
Подготовка к контрольной работе по теме "Неравенства. Системы неравенств" (8 класс)
Категория:
Алгебра
09.05.2025 20:07
© 2025, Хоцкая Наталья Васильевна 108 1


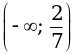 .
.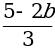
 ;
;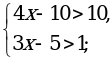 б)
б) 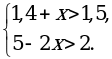
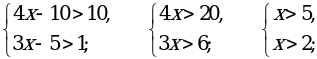
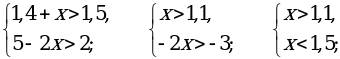
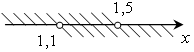 (1,1; 1,5).
(1,1; 1,5).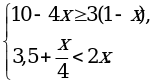
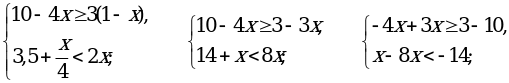
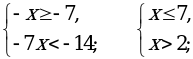
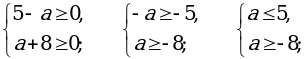
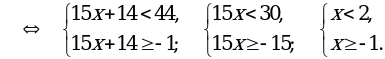
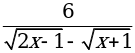 входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.
входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.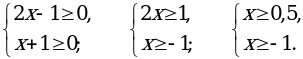
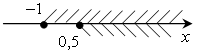
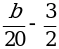 ;
; 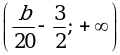 .
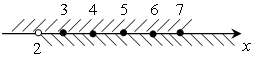
. (–∞; –4]
(–∞; –4]


















